logo资料库

Vensim函数说明.doc

发布时间：2022-06-09 发布人：admin 分类：说明书 资料大小：0.08M 资料格式：doc 举报 版权申诉
第1页 / 共10页
第2页 / 共10页
第3页 / 共10页
第4页 / 共10页
第5页 / 共10页
第6页 / 共10页
第7页 / 共10页
第8页 / 共10页
资料共10页，剩余部分请下载后查看
    第 8 章 Vensim PLE 软件包中系统动力学函数 系统动力学所以能处理复杂的系统问题，除提出流位流率系简化流率基本入 树建模法去描述系统外，还有一个重要原因是其专用软件都设计了一系列通用的 系统动力学函数。 第一节 数学、逻辑、测试函数 § 8.1.1 数学函数 Vensim PLE 备有五种普通数学函数供用户使用。 1．SIN（X） 定义 1：SIN（X）为三角正弦函数，X 须以弧度表示，其值小于 8.35×105 当自变量是角度时,应通过乘以 2π/360 转化为弧度。 2．EXP（X） 定义 2：EXP(X) = eX ，e 是自然对数的底，e=2.7182…，X 的值必须小于 36。 人们常用指数函数去描述系统，有了上面函数将会带来很大方便。 3. LN（X），变量 X 大于零。 即以 e 为底的对数函数，它与 EXP（X）互为反函数，这样可以用 EXP（X） 和 LN（X） 来计算非以 e 为底的幂函数和对数函数。 4. SQRT（X）=√X—，X 必须是非负量。 5. ABS（X） = │X│，对 X 取绝对值。 § 8.1.2 逻辑函数 逻辑函数的作用类似于其它计算机语言中的条件语句，Vensim PLE 的逻辑函 数有三种。 1. 最大函数 MAX（P，Q） MAX 表示从两个量中选取较大者，P 和 Q 是被比较的两个量，结果也是在这两 个量中选取。 定义 1：若 MAX（P，Q）= P 若 P≥Q Q 若 P≤Q 其中 P，Q 是变量或常量，则 MAX（P，Q）为最大函数。 可用 MAX 函数从多个量中选取较大者。如从 P，Q，D 三个量中选择较大者可 用：MAX（D，MAX（P，Q））。 最小函数 Q 若 P≥Q 定义 2：若 MIN（P，Q）= P 若 P≤Q 则 MIN（P，Q）为最小函数。 １． MIN 同 MAX 一样，可以从 MIN（P，Q） 基本功能中派生出各种用法。 3. 选择函数 IF THEN ELSE(C,T,F) 定义 3：若 IF THEN ELSE(C,T,F) T C 条件为真时 1
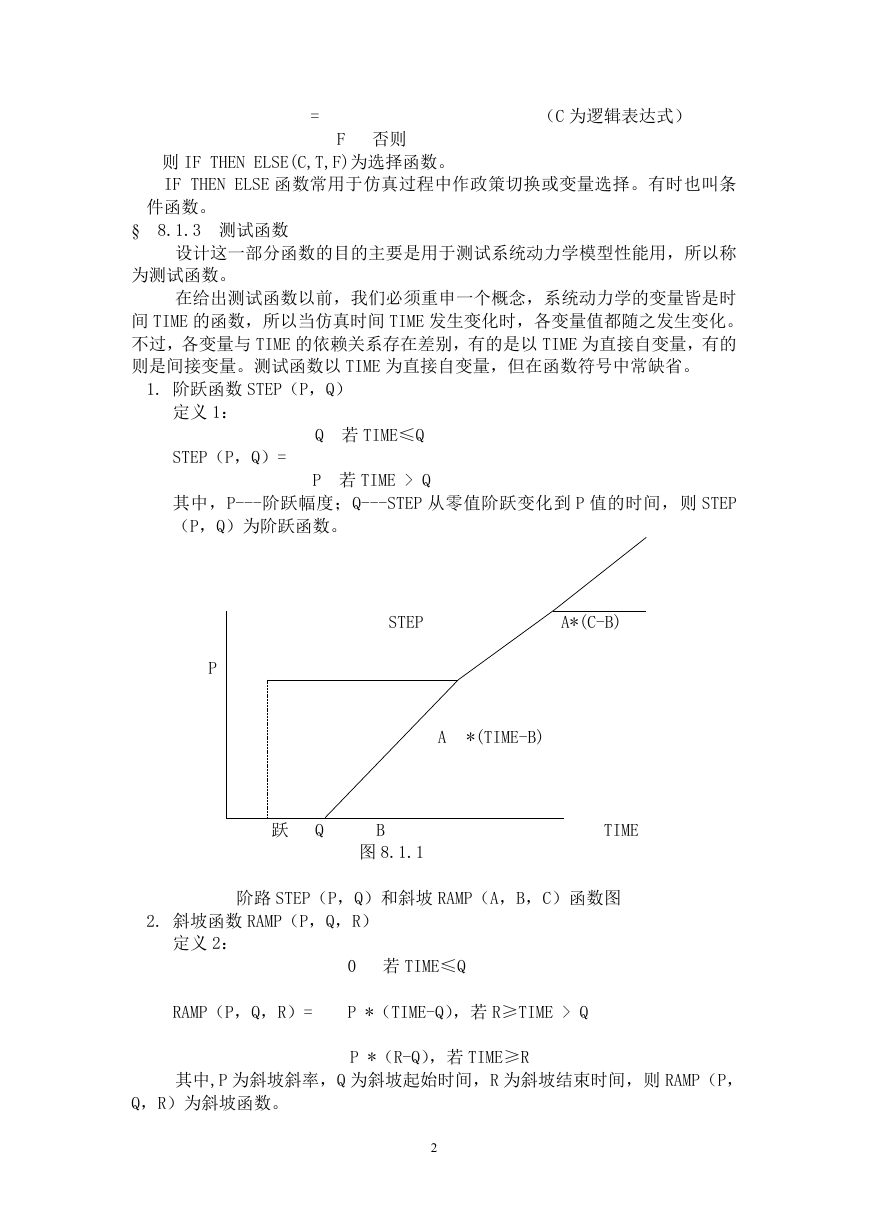
    = F 否则 （C 为逻辑表达式） 则 IF THEN ELSE(C,T,F)为选择函数。 IF THEN ELSE 函数常用于仿真过程中作政策切换或变量选择。有时也叫条 件函数。 § 8.1.3 测试函数 设计这一部分函数的目的主要是用于测试系统动力学模型性能用，所以称 为测试函数。 在给出测试函数以前，我们必须重申一个概念，系统动力学的变量皆是时 间 TIME 的函数，所以当仿真时间 TIME 发生变化时，各变量值都随之发生变化。 不过，各变量与 TIME 的依赖关系存在差别，有的是以 TIME 为直接自变量，有的 则是间接变量。测试函数以 TIME 为直接自变量，但在函数符号中常缺省。 1. 阶跃函数 STEP（P，Q） 定义 1： STEP（P，Q）= Q 若 TIME≤Q P 若 TIME > Q 其中，P---阶跃幅度；Q---STEP 从零值阶跃变化到 P 值的时间，则 STEP （P，Q）为阶跃函数。 STEP A*(C-B) P A *(TIME-B) 跃 Q B 图 8.1.1 TIME 阶路 STEP（P，Q）和斜坡 RAMP（A，B，C）函数图 2. 斜坡函数 RAMP（P，Q，R） 定义 2： 0 若 TIME≤Q RAMP（P，Q，R）= P *（TIME-Q），若 R≥TIME > Q 其中,P 为斜坡斜率，Q 为斜坡起始时间，R 为斜坡结束时间，则 RAMP（P， P *（R-Q），若 TIME≥R Q，R）为斜坡函数。 2
    3. 脉冲函数 PULSE(Q,R) 定义 3: 若 PULSE(Q,R)随 TIME 变化产生脉冲。 其中： Q---第一个脉冲出现的时间 R---相邻两个脉冲的时间间隔 脉冲宽度为仿真步长，则 PULSE(Q,R)为脉冲函数。 4．均匀分布随机函数 RANDOM UNIFORM（A，B，S） 定义 5：RANDOM UNIFORM（A，B，S）产生在区间（A，B）内的均匀分布随 机数，S 给定随机数序列就确定，S 取不同的值产生随机数序列也不同。RANDOM UNIFORM（A，B，S）为均匀分布随机函数。 上面我们给出了四种测试函数，实际上还有前面数学函数 SIN（X）等也可 以作为测试函数。 一个系统动力学模型，可以通过改变常数再运行的办法，实现多种测试 函数分别进行测试。 第二节 表函数 § 8.2.1 表函数表示形式 1. Vensim PLE 中表函数表示形式 定义 1 自变量与因变量的关系通过列表给出的函数叫表函数。例如下表就确 定了一个表函数。 自变量 X 0 因变量 Y 0.5 1 1 1 1.5 2 2 5 2.5 10 表函数是系统动力学的一个重要特征,它用于建立两个变量之间的非线性关系, 特别是软变量之间的关系。例如：员工士气对工作效率的影响程度。一般，两个 变量先归一化或者先规整化，再根据经验给出大致的关系图来。这样设计的变量 是无量纲量。在进入 Vensim PLE 软件 Equation Editor，即点去图标 Y=X2 后， 若方程还未定义，有 AS Graph 选项。选择此选项，会出现下面对话框。该对话 框用于图形化定义，上例表函数可直接填入框中(图 8.2.1)。包括自变量和函数 值即因变量值列举，自变量和函数的最大值等。当自变量为非已知统计点时，可 用线性插值法取其近似值。用鼠标左键在图形框中点按，会自动构成图形。 Vensim PLE 软件中表函数表达形式还可通过选择方程类型 TYPE 中 Lookup 进行列举表出，即把表函数自变量，因变量最大值、最小值及一些自变量与因变 量对应的点值列出。如上例描述的表函数可以在方程输入框写成： [（0,0）-（10,10）]（0,0.5）（1,1）（1.5,2）（2,5）（2.5,10）其中[ ]中前 面( )中 0,0 分另为自变量、因变量最小值，若自变量小于最小值，因变量取 最小值，后面（ ）中 10，10 分别为自变量、因变量最大值，若自变量超出最 大值，因变量取最大值，[ ]后面五个（ ）是已知自变量和因变量对值点，若 自变量值不在给出点中，则自动用线性插值法求因变量对应值。自变量、因变 量的最小值、最大值可依据实际背景来确定，列出的对应值点作为已知点可从 历史数据中计算或分析给出。Vensim PLE 专用软件对表函数的增减性、取值 3
    间隔均匀性没有严格要求，但使用者可根据实际问题给出取值间隔、分段满足 增减性的表函数。在 Vensim PLE 中建立的入树或流图内一个表函数必须有三 部分完成，即一个自变量 X,一个因变量 Y 及一个 Y 关于 X 的因子表，其因果 关系为： Y 变量 ↗ X 因子表 ↖ X 变量 方程可写为： Y 变量=X 因子表（X 变量） 上例表函数中 X 因子表=[（0,0）-（10,10）]（0,0.5）（1,1）（1.5,2）（2,5）（2.5,10） 表函数的建立方法将在§8.2.2 介绍。 2. Micro DYNAMO 及 PD PLUS 中表函数表示形式与 Vensim PLE 软件不同的是在 Micro DYNAMO 及 PD PLUS 中有特定不同类型，其表示含义可由定义给出并固 定下来。现使用 Vensim 软件的读者，可以不阅读下面内容。 ⑴ Micro DYNAMO 两类表函数 定义 1：若 TABLE（TY，X.K，XLOW，XHIGH，XINCR） 中： TY---表量名（因变量已给值） X---自变量 XLOW---自变量 X 的最小值 XHIGH---自变量 X 的最大值 XINCR---自变量 X 的取值间隔 自变量取值为 XLOW 至 XHIGH 间以等间隔 XINCR 取 X1，X2，…… Xm m 个值，且 m =（XHIGH-XLOW）/XINCR + 1 对应于 X1，X2，…… Xm 的 TY 的值在 DYNAMO 方程中以 T 方程： T TY= E1/E2/……/E m 给出。 当 X0∈（XLOW，XHIGH），但 X0≠Xi（i=1,2,…,m）时，其变量值按线性插法给出， 当 X 的值超出[XLOW，XHIGH]范围时，因变量取对应的端点值，并给出警告信息。 则 TABLE(TY，X.K, XLOW, XHIGH, XINCR）称为第一类表函数。 T TY= E1/E2/……/E m 称为其表量语句，又称为 T 语言。 例 1：已知两变量 X 和 Y，因变量 Y 随自变量 X 变化的关系的曲线所示(图 8.2.2) 自变量 X 从 X=-3 开始，按等距离取 7 个点得表 8.2.1。设 Y 为辅助变量，用第 一类表函数语句表示的 DYNAMO 语句为： A T Y.K=TABLE（TY,X.K.-3.3.1） TY =-20/0/10/16/20/24/30。 X Y -3 -20 -2 0 -1 10 0 16 1 20 2 24 3 30 表 8.2.1 注 1：该例在 Vensim PLE 中变量关系图为： Y 变量 ↗ X 因子表 ↖ X 变量 方程可写为： Y 变量=X 因子表（X 变量） 4
    子 表 因 X - （3,20）](-3,-20),(-2,0),(-1,10),(0,16),(1,20),(2,24),(3,30) （曲线如 图 8.2.3） -3,-20 ） = [ （ 当 X 值超出[-3,3]时，Y 取对应的端点值，不给出警告信息。 定义 2：若 TABHL（TY，X.K，XLOW，XHIGH，XINCR）中随 X 的取值范围超出[XLOW,XHIGH] 时,因变量取对应的端点值,但不给出错误信息外,其它内容与第一类表函数相同, 则 TABHL(TY，X.K，XLOW，XHIGH，XINCR）称为第二类表函数。 注 2：在 PD PLUS 语言中，表函数中 T 语句中斜线改为了逗号，且定义了下面两 类表函数，不妨称为第三、第四类表函数。 第三类表函数为：TABXL（TY，X.K，XLOW，XHIGH，XINCR），此表函数，除 X 取 值范围超出[XLOW，XHIGH]范围时，因变量取端点的趋势外推值外，其它内含与 第一类表函数相同。 第四类表函数为：TABPL（TY，X.K，XLOW，XHIGH，XINCR），此表函数除利用多 项式使曲线在各点起滑连接代替线段连接外，其它含义与第 一类表函数相同， 但表量语的数值后要加上 m 个零，如，对前面第一类表函数的例子，改为 TABPL， 则写为： A T Y.K=TABPL（TY,X.K.-3.3.1） TY =-20，0，10，16，20，24，30，0，0，0，0，0，0，0。 §8.2.2 表函数建立方法介绍 前面介绍的 Vensim PLE 专用软件，DYNAMO 语言表达表函数的方式，是比较 简单、容易接受的，但一个表函数的建立却不是如此容易的，往往是一个定性与 定量相结合反复分析的结果，要建立一个具体表函数，肯定必须考虑所涉及的自 变量、因变量的实际背景，再仔细研究其包含的一般数学问题及一般统计问题， 进行深层次的量化分析，最后得出能反应变量间一般关系规律的量表作为表函数 才能用于 SD 模型，日常生活中，可以经常碰到时间间隔相同的统计年报表、季 报表、月报表，这些都是表函数。但是，在建立一个实际系统的 SD 模型时，这 些统计报表很难作为一个完整的表函数直接放入模型中。其一，表函数不一定以 时间为自变量，实践表明，表函数的自变量很多是同模型中其它一个或若干个变 量的因变量；其二，统计报表没有未来若干年的预测数据，而 SD 模型的目标重 点在对未来规律的仿真。根据以上分析和以往的经验，建立一个具体表函数，必 须涉及下面基本步骤： 一、 确定变量变化范围及取值间隔： 首先根据实际背景，初步统计或估计因变量，自变量变化范围，即最小值、 最大值，再依据获取数据的难易程度及灵敏度、精确度的要求来确定变量点 间的取值间隔，由于 Vensim PLE 中自变量间隔不一定要求均匀，在定取值 间隔时可依实际背景把变量范围看作一个阶段或若干阶段来定，在不同阶 段，取值间隔可不一样，目的是必须准确反应变量间变化规律。 二、 确定函数的变化趋势 根据变量间因果关系极性来确定函数的增减规律，对整个变量范围要进行分 析，可能某阶段呈递增态，另一个阶段呈现递减态，有的阶段不明显，根据 5
    变化幅度大小可以调整各阶段取值间隔点间隔及点密度。 三、 找出特殊点与特殊线 针对一个实际系统，建立 SD 模型，调用的表函数往往涉及到一些特殊取值 点，如极值点、参照点、临界点，若有这些起点，在用 Vensim PLE 时，最 好能直接给出在表函数的表达形式中，比如一个表函数的因变量 Y 是模型中 其它变量乘积因子，最好找出 Y=1 对应的自变量 X，把（X，1）直接放入表 函数表达式中；如 Y 是模型中其它变量的和式，最好找出 Y=0 对应的自变量 X，把（X，0）直接放入表函数表达式中；如 Y=Y0 是表函数单调性改变的点， 最好找出相应自变量 X0，把（X0，Y0）直接放入表函数表达式中，等等。虽 然表函数一般情况下是非线性的，但不排除在某阶段呈线性，若在某阶段呈 线性，可在表函数表达式直接给出此阶段的两端点，（X1，Y1），（X2，Y2）。（此 两点代表确定的那条直线）。特殊线是指 Y=X，Y=Y0 或 Yˊ= X0，的一些线段， 反映了表函数的某种特征，若有，最好能直接给出。对于如何确定特殊点、 特殊线，必须据实际背景，采用各种系统工程方法来定，可参考后面表函数 实例。 四、 确定斜率 这里讲的斜率主要是指非特殊点的变化情况，在一个表函数中除找出特 殊点外，更重要的是非特殊点的变化规律，在 Vensim PLE 中，表函数表达 式内必须列出反应变化规律的若干非特殊点，这些点通过分析历史数据、预 测数据得到，直接关系到表函数是否有效，其分析方法可根据实际背景借用 各种相关理论及技术手段。 为了让读者更直观的了解表函数的建立过程，下面给出二个现有 SD 模型 的表函数进行简单分析。 例 1： 如图 8.2.4 为一个城市建设简化模型中剩余可建面积对其事业单位新建面 积的影响因子 ELBC 关于已占有土地比 LFO 的表函数，即 ELBC=f（LFO），两个变 量均为无量纲，此函数无法用基本初等函数表示，但可采用定性定量相结合的方 法建立表函数。 第一步：确立自变量 LFO 的变化范围及间距。 假设建模研究时，已建土地比是 0.1,又不考虑土地余留，故 LFO 变化范围 为[0.1,1]。对于[0.1,1]区间如何等份？根据整个模型的精度要求及日常实际， 分成 9 个等份。间隔取 0.1 为宜。因若在仿真中 LFO 需取两位小数，也可由表函 数的线性取值办法解决(因一般统计土地比只保留到两位小数)。 第二步：确定函数增减性。 当 LFO∈[0.1,0.4]时，ELBC 随 LFO 递增 当 LFO∈[0.4，1]时，ELBC 随 LFO 递减 前式表明年新增长面积随城市建筑的增多而增加。这是因为，在城市发展的 早期阶段，大量土地有待开发，且已有企事业单位的建成会为更多企事业单位的 建立创造了有利的条件。如砖厂促进了建筑加快；路面的铺砌使材料运输更方便、 更迅速；水、气、电企事业单位建立能提供生活基本保障。另外，经实地分析， 当已占土地比不超过 40%时，建地挑选也有更大余地。出于上述定性分析得前式 成立。 根据定性分析，与其它城市建立的历史事实横向比较，已占面积 LFO 超 40% 6
    以后，由于各种主要类型企事业单位已基本建立，市场供给网已基本建立，好的 建筑环境为数不多，建筑土地资金费相应增加，这些都制约着开发地区的年建筑 面积的新增，则有后式成立。 第三步：确定特殊点。 1、由历史统计数据，当土地面积比 LFO=0.1 时,年新增建筑面积比为 60%, 则 0. 7×ELBC=0.6, ELBC=0.86 得点(0.1,0.86) 2、有企业建设年新建面积方程分析，当 LFO=0.2 时，ELBC=1 3、确定极大值点 LFO=0.4 时，ELBC 的值，这是一个预测值，确定这种值， 系统动力学本身未提供有效的方法，一般建模者常借用其它预测方法来 帮助解决，如借用特尔菲方法，趋势外推，时间序列法，回归分析法、 GM 模型等方法。最简单的是专家咨询法。通过定性分析的 ELBC 最大值 为 1.1。得特殊点（0.4，1.1）。由实际情况，显然还有特殊点（1，0）。 第四步：确定斜率 也就是确定非特殊点对应的 ELBC 值。这些数据来自两部分，一部分是历 史数据，另一部分是预测数据。据系统分析综合两部分结果，参考有关 资料得到了图 8.2.5 的表函数。 例 2： 如图 8.2.5 为我们建立的珠海市宏观经济 SD 模型中建城区绿地面积第三产 业影响因子关于第三产业指数的表函数。这里第三产业指数是第三产业增加值的 函数，根据珠海市的实际情况，珠海市 1997 年的建城区绿地面积占有率作为标 准年，即当第三产业增加值为珠海市 1997 年实际值时，第三产业指数为 1，这 样得到了表函数的特殊点（1，1），根据珠海市第三产业的发展规模和速度，第 三产业指数的取值范围定为 0.5 到 10，根据珠海市过去的绿地面积占有率和城市 的发展理念，对比 1997 年的情况，建城区绿地面积第三产业影响因子的取值范 围定为 0.9 到 2，珠海市是一个高度重视环境绿化的城市，近几年其绿地占有率 逐年上升，可以预知随着第三产业的发展，绿地面积占有率还会提高，最后达到 一个较稳定的数据，通过以上分析和专家咨询，综合珠海市的发展规划得到了上 面图 8.2.5 表函数。该表函数可以随时根据珠海的发展进行调整，适当的时候可 纳入珠海市的宏观调控计划模拟中。此 SD 模型在珠海市已使用了两年，得到了 各方面的肯定，表函数的功能得到了充分发挥。 第三节 延迟函数 §8.3.1 Vensim PLE 中延迟函数表示及使用方法 一、定延迟函数的概念 义 1 量变化需要经过一段时间的滞后才能得到响应，这种现象称为延迟。 刻划延迟现象的函数称为延迟函数。 延迟是系统动力学中一个重要概念，因为在系统中存在大量延迟现象，例 如培训的学员要经过一段时间才能发挥作用；投资要经过一段时间才能成为 新的增生产能力；人得病，有潜伏期；污染物排放到江河之中，要经过扩散 才能使江河发生污染等。另外，延迟函数的构造丰富了系统动力学理论。 7
    二、延迟函数的分类 发生的物流流线上的延迟称为物流延迟；发生在信息流线上的延迟称为 信息延迟。 根据以上概念，原则上所有的物流和信息流，在其流线上都会出现延迟，但 我们在建模时，应抓住主要延迟进行设计，才能使复杂与精确性得到统一。由物 流和信息流的不同，延迟函数分为物流指数延迟函数和信息延迟函数，在 Vensim PLE 中其函数名有固定的表示形式，分别为 DELAY1、DELAY2、DELAY3 和 SMOOTH、SMOOTH3 等。 三、使用方法 延迟函数在 Vensim PLE 软件中直接给出，其函数在用到时可直接调用。图 8.3.1 是仓存 Invent.dml 模型的简化流率基本入树，其中变量接到的订单 ORDRCV 是关于延迟时间 DEL 的延迟函数变量，其方程为： 接到的订单 ORDRCV=DELAY3（订单率 ORDRS，延迟时间 DEL） 流位方程为： 仓存 INV=INTEG（接到的订单 ORDRCV-货运率 SHIP，期望的仓存 DSINV） 在此该延迟变量可以不出现在入树或流图中，而可以直接放在流位方程中， 这样在入树或流图中保证了流率对流位的直接作用对应关系，此时流位方程可直 接写为： 仓存 INV=INTEG（DELAY3（订单率 ORDRS，延迟时间 DEL）-货运率 SHIP， 期望的仓存 DSINV），其运行结果和前面一样。下面是仓存 invent.dml 模型的所 有方程，其中 TEST 是测试变量由测试函数组成，上机对 TEST1、TEST2、TEST3、 TEST4 中的某个赋值 1，其余的值仍为零，观察运行结果可以通过测试函数了解 该模型变量的实增、稳态的下降、振动和随机扰动，这样能帮助我们弄清楚模型 的反馈结构及其动态行为之间的联系（有兴趣的读者可以上机试试）。 (01) 标准货运 NSHIP= 100 Units: 货运单位/周 STEP(10, 2 )*TEST1+TEST2*RAMP(20, 2 , 20 )+TEST3*PULSE(2, (02) 测试输入量 TEST= 200)+TEST4*RANDOM UNIFORM (-5, 5 , 0.25) Units: **undefined** (03) 仓存调整时间 IAT= 2 Units: 周 (04) 仓存调整 INVADJ= Units: 货运单位/周 (期望的仓存 DSINV-仓存 INV)/(仓存调整时间 IAT) (05) 仓存 INV= INTEG ( 8
    分享到：
    赞 收藏

    相关推荐

    资料库

    课程资源

    共收录17145份资料，累计13个分类，关注成员有19位，主要包括：PHP,网络管理,网页制作,Java,.Net,数据库,3G/移动开发,C/C++,游戏开发,嵌入式,讲义,软件测试,专业指导

    热门标签

    PHP 网络管理 网页制作 Java .Net 数据库 3G/移动开发 C/C++ 游戏开发 嵌入式 讲义 软件测试 专业指导

    最新资料