第1页 / 共19页
第2页 / 共19页
第3页 / 共19页
第4页 / 共19页
第5页 / 共19页
第6页 / 共19页
第7页 / 共19页
第8页 / 共19页
OSPF Dijkstra 算法更新路由表.doc
1需求分析
1.1课程设计目的
1.2课程设计要求
1.3运行环境
2概要设计
2.1最短路径算法的分类
2.2 Dijkstra算法的基本原理
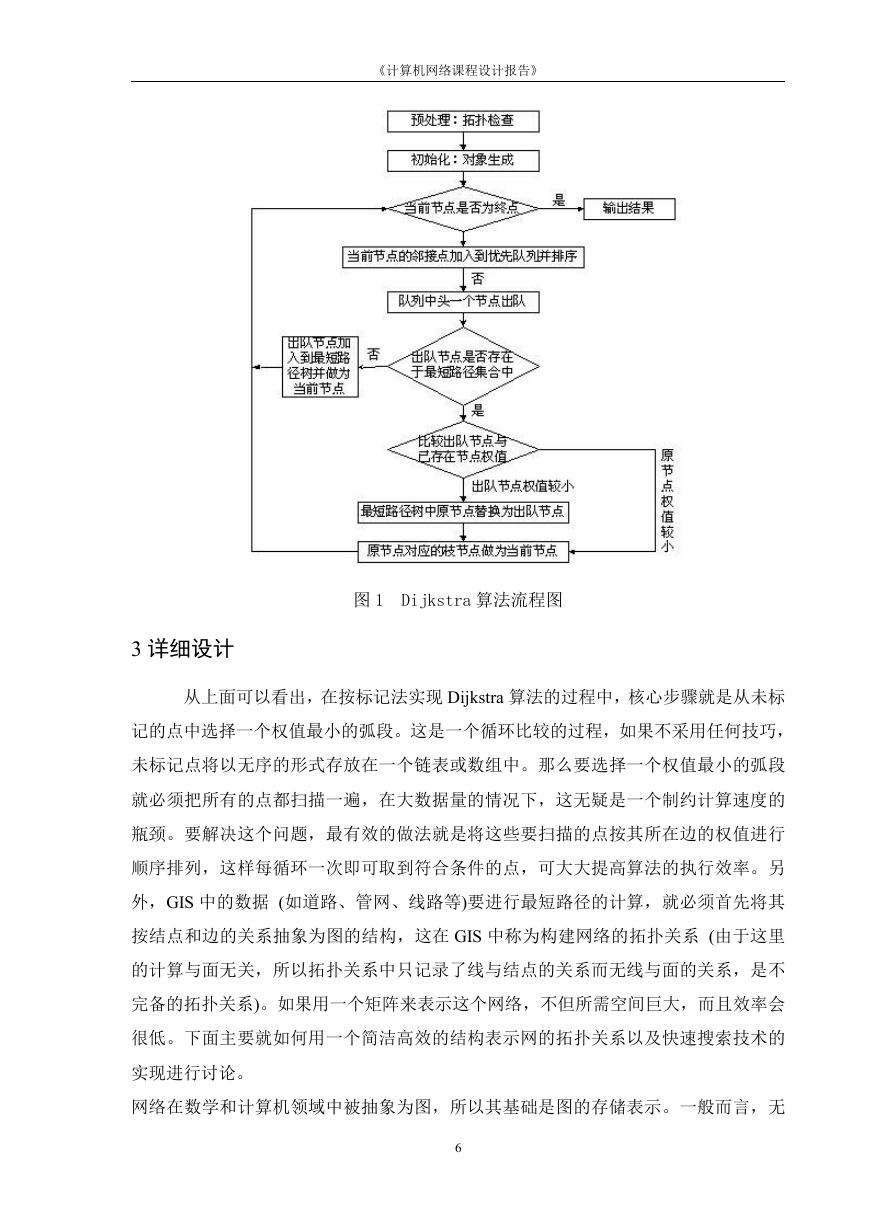
2.3 Dijkstra算法的步骤
3详细设计
4调试与操作说明
4.1课程设计程序源程序
#include
#include
typedef int Status;
typedef Status ** Node;//node指针的指针
#define MaxNum 10000;//设置10000为无穷
#define FALSE 0;
#define TRUE 1;
Node Build (Status num )
{
int i,j,k;
Node a;
a=(Node) malloc( num * sizeof (Status *));
printf("\n请输入各路由边线的cost的权值 ，如果不存在真接连接请输入10000\n
for(i=0;i
{
a[i]=(Status *) malloc( num * sizeof (Status))
for(j=0;j
{
a[i][j]=MaxNum;
}
}
for(i=0;i
{
for(j=0;j
{
if(i!=j)
{
printf("请输入第%d个结点到第个%d结点到的权值",i+1,j+1);
scanf("%d",&k);
/*if( i>=num || j>=num )
{
printf("无效的输入!请重新输入!!");
exit(1);
}*/
a[i][j]=k;
}
else
a[i][j]=10000;
}
}
return a;
}
void ShortestPath_DIJ( Node a ,Status i ,Status v0
{
int v,w,j,l=1;
Status *final;//设置int 指针
Status min;
final=(Status *)malloc( sizeof(Status)*i );//分配空间
for(v=0;v
{
final[v]=FALSE;
pre[v]=FALSE;
D[v]=a[v0][v];
if(D[v]<10000)//找到头结点
pre[v]=v0;
}
for(v=0;v
{
if( a[v0][v]>=10000 )
l++;
}
if(l>i)
{
printf("\n从路由%d出发没有最短路径到其他端点!\n",v0+1);
exit(0);
}//v0是一个孤立的顶点
D[v0]=0;
final[v0]=TRUE;
for( j=0 ; j
{
min=MaxNum;
for( w=0 ; w
{
if( !final[w] )//判断是否已被最短路径路过
{
if( D[w]
{
v=w;
min=D[w];
}//找出最短的路径
}
}
final[v]=TRUE;
for( w=0 ; w
{
if( !final[w] && ( (min+a[v][w])
{
D[w]=min+a[v][w];
pre[w]=v;
}
}
}
}
void Show(Status *D , Status *pre ,int i ,int v0)/
{
int j,k,m,n;
int *temp;
temp=(int *)malloc(sizeof(int)*i);
for(j=0;j
{
if(j!=v0)
{
printf("\n路由[%d]到路由[%d]的最短路径长度为:%3d " ,v0+1,j+
n=j;
if(D[j]!=10000)//判断是不是有可达路径
for(k=0;k
{
temp[k]=pre[n];
if(temp[k]!=v0)//判断是不是源点自身
n=temp[k];
else
//(temp[k]==v0)//是源点跳出
break;
}
if( k==0&&D[j]!=10000&&D[j]!=0 )//当是源点时
{
printf("路由[%d]->路由[%d]",v0+1,j+1);
}
if( k!=0 &&D[j]!=10000&&D[j]!=0)//不是源点时
{
for(m=k;m>=0;m--)
{
printf("路由[%d]->",temp[m]+1);
}
printf("路由[%d]",j+1);
}
if(D[j]==10000)//没有路径
{
printf("从路由[%d]出发没有最短路径到路由[%d]!",v0+1,j+1);
}
if(D[j]==0)
{
printf("路由[%d]",v0);
}
}
}
}
void main()
{
int i,v0,choice;
int w;
Node a;
Status *D,*pre;
while(1)
{
start1:
printf("\n 请选择：\n");
printf(" 1.自己制作路由拓补图\n\n");
printf(" 2.退出!\n\n");
printf("请输入你的选择：");
scanf("%d",&choice);
if(choice==2)
break;
else if(choice>3||choice<0||choice%1!=0)
{
printf("ERROR!请重新选择\n");
goto start1;
}
switch(choice)
{
case 1:
start:
printf("请输入网络拓补中路由器总数:");
scanf("%d",&i);
if(i<=0|| i%1 !=0)
{
printf("你输入的路由器的个数有误，请重新输入\n");
goto start;
}
//printf("input the arcs:");
//scanf("%d",&j);
D=(Status *)malloc(sizeof(Status)*i);//用于存放最短路径
pre=(Status *)malloc(sizeof(Status)*i);//用于存放最短
a=Build(i);
//printf("please input the start node: ");
//scanf("%d",&v0);
/*if(v0>i)
{
printf("input errors!not excite this node!");
exit(1);
}*/
break;
}
for(v0=1;v0<=i;v0++)
{
ShortestPath_DIJ( a ,i ,v0-1 ,D , pre );
Show( D, pre, i, v0-1 );
}
printf("\n\n你是否还想再尝试一次?是请输入1,不想请输入0结束！\n请选择：");
scanf("%d",&w);
if(w!=1)
break;
}//while
}
4.2程序输出图
图4.2.1
图4.2.2
图4.2.3
4.3设计结果分析
总结
致谢
参考文献
《计算机网络课程设计报告》
计 算 机 网 络
摘要：
OSPF 采用 SPF（Shortest Path First）算法（也叫做 Dijkstra 算法），SPF 算法是链
路状态型算法，链路状态型算法对自己以及其它路由器产生的链路状态信息进行汇总，
在本地生成一个链路状态数据库，来对此数据库进行运算，从而得到一张以自己为根
的、到达其它各目的节点最近的一张路径图，根据算法和协议特点，这张图是无环路
的。
本次课程设计是模拟最短路径优先协议(ospf)路径选择算法，使用邻接矩阵存储
图的有关信息，用迪杰斯特拉(Dijkstra)算法得出最短路径，并附有弗洛伊德(Floyd)
算法加以比较。另为了更好的对 Dijkstra 算法和 Floyd 算法有更好的理解在对其又做
了改进-----使其能生成多源结点到多结点的最短路径及相应的最短路径的权值。
关键词：
C++语言 最短路径优先协议(ospf) 迪杰斯特拉（Dijkstra）
最短路径
最短路径长度
邻接矩阵
1
《计算机网络课程设计报告》
目录
1 需求分析......................................................................................................................................................... 3
1.1 课程设计目的..........................................................................................................................................3
1.2 课程设计要求..........................................................................................................................................3
1.3 运行环境..................................................................................................................................................3
2 概要设计......................................................................................................................................................... 4
2.1 最短路径算法的分类..............................................................................................................................4
2.2 Dijkstra 算法的基本原理........................................................................................................................4
2.3 Dijkstra 算法的步骤................................................................................................................................5
3 详细设计......................................................................................................................................................... 6
4 调试与操作说明............................................................................................................................................. 8
4.1 课程设计程序源程序..............................................................................................................................8
4.2 程序输出图............................................................................................................................................15
4.3 设计结果分析........................................................................................................................................16
总 结................................................................................................................................................................17
致 谢................................................................................................................................................................18
参考文献.............................................................................................................................................................. 19
2
《计算机网络课程设计报告》
1 需求分析
1.1 课程设计目的
本次课程设计要在 VC++环境的最短路径，常用得有 Dijkstra 算法和 Floyd 算法
等，这次主要应用 Dijkstra 算法。Dijkstra(迪杰斯特拉)算法是典型的最短路径路由
算法，用于计算一个节点到其他所有节点的最短路径。主要特点是以起始点为中心向
外层层扩展，直到扩展到终点为止。Dijkstra 算法能得出最短路径的最优解，但由于
它遍历计算的节点很多，所以效率低。Dijkstra 算法是很有代表性的最短路算法，在
很多专业课程中都作为基本内容有详细的介绍，如通信有原理，图论，运筹学等等。
通过本次通过这次课程设计，我们要对上课所学得知识进行巩固，掌握图、子图、
结点的度数、有向图、无向图、多重图、完全图、补图、生成子图、图的同构、路、
回路、连通图、弱连通、强连通等概念及其性质；掌握图的矩阵表示，给定图的邻接
矩阵会求任一结点的入度、出度和度数；一个结点到另一个结点长度为 k 的路径的条
数；该图的可达性矩阵。
对最小生成树、最短路径、Dijkstra 算法，最短路由有了更深得理解。本次课程
实验，要了解最短得路由得算法，掌握 Dijkstra 算法得概念，基本原理和思想。
1.2 课程设计要求
根据所学数据结构基础知识，使用迪杰斯特拉（Dijkstra）算法，编写一 C++程
序，它能根据读入得带权有向图 G 的数据，构造并输出图 G 的顶点 Vi 到其它每个顶点
的最短路径及长度，并输出其最短路径。设计具体要求：实现以下几个功能：
（1）、实现图的建立；
（2）、用邻接矩阵存储图的信息；
（3）、用不同的算法实现在已建图中最短路径的选择
（4）、输出最短路径的权值和相应的路径。
1.3 运行环境
该程序的运行环境为 Windows XP 系统，Microsoft Visual C++6.0 版本。
3
《计算机网络课程设计报告》
2 概要设计
2.1 最短路径算法的分类
所谓最短路径（shortest path）问题指的是：如果从图中某顶点出发（此点称
为源点），经图的边到达另一顶点（称为终点）的路径不止一条，如何找到一条路径
使沿此路径上各边的权值之和为最小。设一有向网络 G =（V,E），已知各边的权值，
并设每边的权均大于零，以某指定 V0 为源点，求从 V0 到图的其余各点的最短路径。
用于解决最短路径问题的算法被称做“最短路径算法”， 有时被简称作“路径算
法”。 最常用的路径算法有：
(1)Dijkstra 算法
(2)A*算法
(3)SPFA 算法
(4)Bellman-Ford 算法
(5)Floyd-Warshall 算法
(6)Johnson 算法
2.2 Dijkstra 算法的基本原理
Dijkstra 算法是由荷兰计算机科学家艾兹格·迪科斯彻发现的。算法解决的是有向
图中最短路径问题。 举例来说，如果图中的顶点表示城市，而边上的权重表示著城市
间开车行经的距离。 Dijkstra 算法可以用来找到两个城市之间的最短路径。 这个算法
是通过为每个顶点 v 保留目前为止所找到的从 s 到 v 的最短路径来工作的。 初始时，
源点 s 的路径长度值被赋为 0（d[s]=0），同时把所有其他顶点的路径长度设为无穷大，
即表示我们不知道任何通向这些顶点的路径（对于 V 中所有 顶点 v 除 s 外 d[v]= ∞）。
当算法结束时，d[v]中储存的便是从 s 到 v 的最短路径，或者如果路径不存在的话是无
穷大。
Dijstra 算法的基础操作是边的拓展：如果存在一条从 u 到 v 的边，那么从 s 到 u
的最短路径可以通过将边(u,v)添加到尾部来拓展一条从 s 到 v 的路 径。这条路径的长
度是 d[u]+w(u,v)。如果这个值比目前已知的 d[v]的值要小，我们可以用新值来替代当
前 d[v]中的值。拓展边的操作一直执行 到所有的 d[v]都代表从 s 到 v 最短路径的花费。
4
《计算机网络课程设计报告》
这个算法经过组织因而当 d[u]达到它最终的值的时候每条边(u,v)都只被拓展一次。 算
法维护两个顶点集 S 和 Q。集合 S 保留了我们已知的所有 d[v]的值已经是最短路径的
值顶点，而集合 Q 则保留其他所有顶点。集合 S 初始状态为空，而后每一步 都有一个
顶点从 Q 移动到 S。这个被选择的顶点是 Q 中拥有最小的 d[u]值的顶点。当一个顶点
u 从 Q 中转移到了 S 中，算法对每条外接边(u,v)进行拓展。
2.3 Dijkstra 算法的步骤
Dijkstra 算法的基本思路是：假设每个点都有一对标号 (dj, pj)，其中 dj 是从起源点
s 到点 j 的最短路径的长度 (从顶点到其本身的最短路径是零路(没有弧的路)，其长度
等于零)；pj 则是从 s 到 j 的最短路径中 j 点的前一点。求解从起源点 s 到点 j 的最短路
径算法的基本过程如下：
(1)初始化。起源点设置为： ds=0, ps 为空;所有其他点: di=∞, pi=?;标记起源点 s，记
k=s,其他所有点设为未标记的。
(2)检验从所有已标记的点 k 到其直接连接的未标记的点 j 的距离，并设置 lkj 是从
点 k 到 j 的直接连接距离。
(3)选取下一个点。从所有未标记的结点中，选取 dj 中最小的一个 i：di=min［dj, 所
有未标记的点 j］点 i 就被选为最短路径中的一点，并设为已标记的。
(4)找到点 i 的前一点。从已标记的点中找到直接连接到点 i 的点 j*，作为前一点,
设置：i=j*
(5)标记点 i。如果所有点已标记，则算法完全推出，否则记 k=i，转到 2) 再继续。
具体流程图如图 1 所示
5
《计算机网络课程设计报告》
图 1
Dijkstra 算法流程图
3 详细设计
从上面可以看出，在按标记法实现 Dijkstra 算法的过程中，核心步骤就是从未标
记的点中选择一个权值最小的弧段。这是一个循环比较的过程，如果不采用任何技巧，
未标记点将以无序的形式存放在一个链表或数组中。那么要选择一个权值最小的弧段
就必须把所有的点都扫描一遍，在大数据量的情况下，这无疑是一个制约计算速度的
瓶颈。要解决这个问题，最有效的做法就是将这些要扫描的点按其所在边的权值进行
顺序排列，这样每循环一次即可取到符合条件的点，可大大提高算法的执行效率。另
外，GIS 中的数据 (如道路、管网、线路等)要进行最短路径的计算，就必须首先将其
按结点和边的关系抽象为图的结构，这在 GIS 中称为构建网络的拓扑关系 (由于这里
的计算与面无关，所以拓扑关系中只记录了线与结点的关系而无线与面的关系，是不
完备的拓扑关系)。如果用一个矩阵来表示这个网络，不但所需空间巨大，而且效率会
很低。下面主要就如何用一个简洁高效的结构表示网的拓扑关系以及快速搜索技术的
实现进行讨论。
网络在数学和计算机领域中被抽象为图，所以其基础是图的存储表示。一般而言，无
6
向图可以用邻接矩阵和邻接多重表来表示，而有向图则可以用邻接表和十字链表示。
《计算机网络课程设计报告》
具体的实现代码如下：
void ShortestPath_DIJ( Node a ,Status i ,Status v0 ,Status *D ,Status
*pre )//a 是传进的矩阵，i 是结点数，v0 是最短路径的源结点
{
int v,w,j,l=1;
Status *final;//设置 int 指针
Status min;
final=(Status *)malloc( sizeof(Status)*i );//分配空间
for(v=0;v=10000 )
l++;
if(l>i)
{
printf("\n 从路由%d 出发没有最短路径到其他端点!\n",v0+1);
exit(0);
}//v0 是一个孤立的顶点
D[v0]=0;
final[v0]=TRUE;
for( j=0 ; j
《计算机网络课程设计报告》
min=MaxNum;
for( w=0 ; w
#include
typedef int Status;
typedef Status ** Node;//node 指针的指针
8
相关推荐
2023年江西萍乡中考道德与法治真题及答案.doc
2012年重庆南川中考生物真题及答案.doc
2013年江西师范大学地理学综合及文艺理论基础考研真题.doc
2020年四川甘孜小升初语文真题及答案I卷.doc
2020年注册岩土工程师专业基础考试真题及答案.doc
2023-2024学年福建省厦门市九年级上学期数学月考试题及答案.doc
2021-2022学年辽宁省沈阳市大东区九年级上学期语文期末试题及答案.doc
2022-2023学年北京东城区初三第一学期物理期末试卷及答案.doc
2018上半年江西教师资格初中地理学科知识与教学能力真题及答案.doc
2012年河北国家公务员申论考试真题及答案-省级.doc
2020-2021学年江苏省扬州市江都区邵樊片九年级上学期数学第一次质量检测试题及答案.doc
2022下半年黑龙江教师资格证中学综合素质真题及答案.doc
