logo资料库

机电系统建模、辨识与控制大作业.doc

发布时间：2022-06-13 发布人：admin 分类：说明书 资料大小：3.63M 资料格式：doc 举报 版权申诉
第1页 / 共31页
第2页 / 共31页
第3页 / 共31页
第4页 / 共31页
第5页 / 共31页
第6页 / 共31页
第7页 / 共31页
第8页 / 共31页
资料共31页，剩余部分请下载后查看
    机电系统建模、辨识与控制
    综合作业
    【作业一】
    考虑如图1.1所示为具有弹性联接的双质量(惯量)伺服系统，要求：
    1）以电动机电枢电压ua为输入、负载角位移θL为输出，建立系统的传递函数模型；
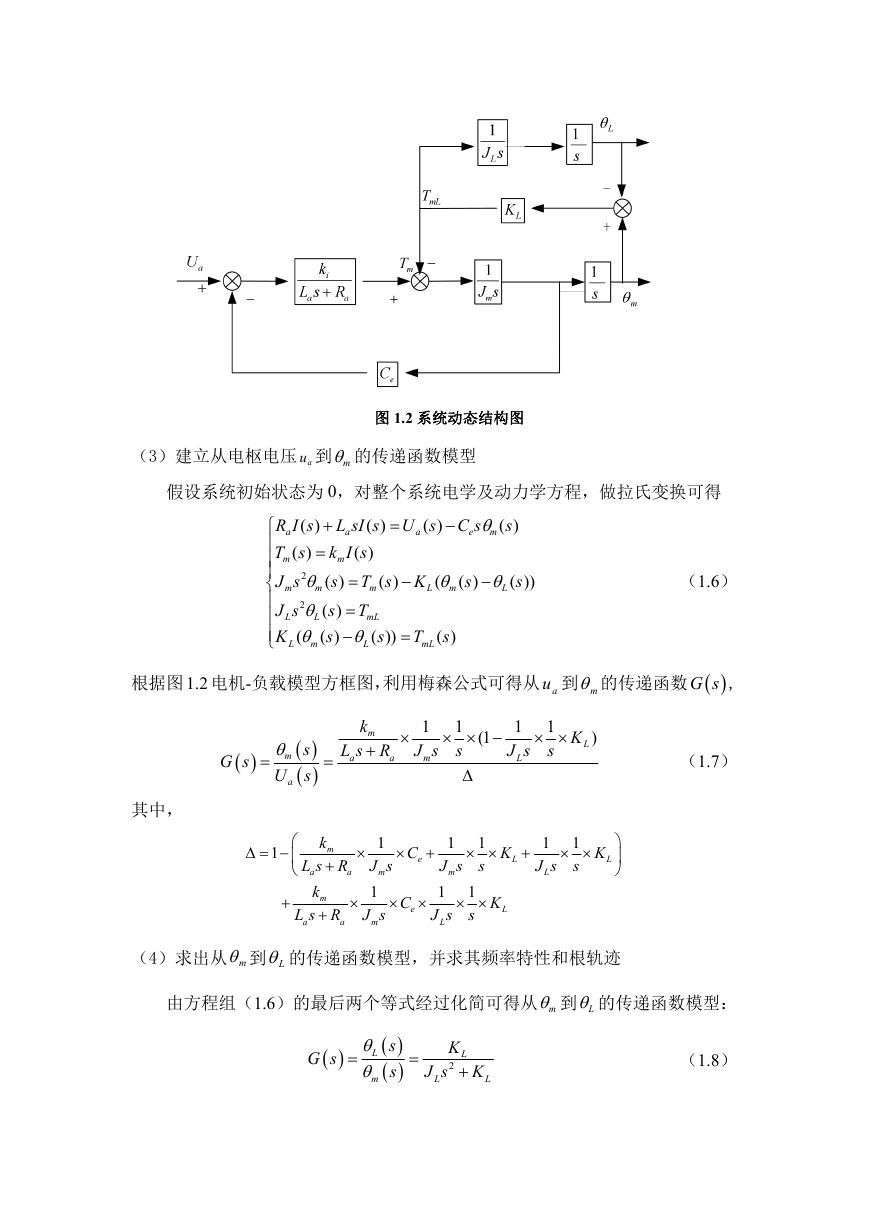
    2）画出系统动态结构图；
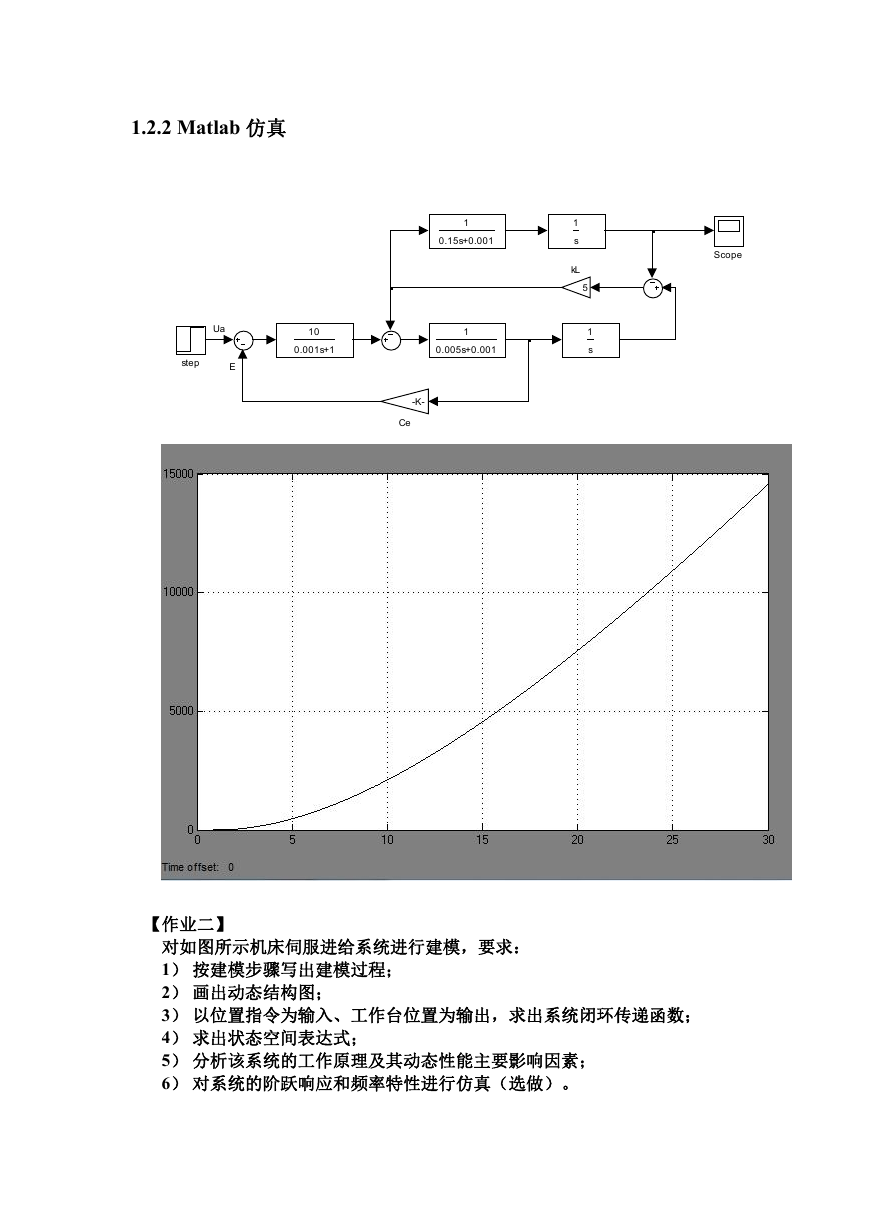
    3）参考下列参数值，对系统的单位阶跃响应进行仿真。
    La=0.001; %L<<1, Inductance of motor armature
    Ra=1.0; % Resistance of motor armature
    Ki=0.001; % Current feedback coefficient
    Jm=0.005; % Equivalent moment of inertia of mot
    bm=0.010; % Viscosity damp coefficient of motor
    km=10; % Motor moment coefficient
    Ce=0.001; % Voltage feedback coefficient
    JL=0.15; % Equivalent moment of inertia of fra
    bL=8.0; % Viscosity damp coefficient of frame
    KL=5.0; % Motor moment coefficient between fr
    图1.1 弹性联接的双质量(惯量)伺服系统
    1.1建模方法综述
    1.1.1传递函数
    1.1.2状态空间方程
    1.2建模分析
    1.2.1系统建模过程
    1.2.2 Matlab仿真
    【作业二】
    对如图所示机床伺服进给系统进行建模，要求：
    1）按建模步骤写出建模过程；
    2）画出动态结构图；
    3）以位置指令为输入、工作台位置为输出，求出系统闭环传递函数；
    4）求出状态空间表达式；
    5）分析该系统的工作原理及其动态性能主要影响因素；
    6）对系统的阶跃响应和频率特性进行仿真（选做）。
    图 2.1 机床伺服进给系统、
    2.1建模方法综述
    2.1.1传递函数
    2.1.2状态空间方程
    2.2建模分析
    2.2.1系统建模过程
    2.2.2系统动态结构图
    2.2.3闭环传递函数及状态空间表达式
    2.2.4状态空间表达式
    2.2.5工作原理及其动态性能主要影响因素
    工作原理
    动态性能分析
    2.2.6仿真
    阶跃响应
    图2.4 阶跃响应曲线
    【作业三】
    给定线性定常离散系统的Z传递函数：
    考虑系统输出测量迭加有白噪声的情况，试分别用最小二乘（RLS）方法、递推最小二乘（RLS）方法和Ka
    1）写出辨识过程与辨识算法；
    2）以Matlab或C/C++语言编程实现上述算法，给出采用三种方法的参数辨识结果；
    3）对后两种方法的辨识过程进行仿真（计算），以采样点（时间）为横坐标，分别绘出对应各个采样点（时间）参数
    3.1最小二乘法
    3.1.1辨识过程及算法
    3.1.2 Matlab仿真
    3.2递推最小二乘算法
    3.2.1辨识过程及算法
    3.2.2 Matlab编程及仿真
    3.3卡尔曼滤波估计法
    3.3.1辨识过程及算法
    3.3.2Matlab编程及仿真
    北京航空航天大学研究生课程考核记录 2014－2015 学年 第一学期 课程名称：《机电系统建模、辨识与控制》 论文题目：《机电系统建模、辨识与控制》综合作业 任课教师评语： 任课教师签字： 考核日期： 年 月 日
    机电系统建模、辨识与控制 综合作业 【作业一】 考虑如图 1.1 所示为具有弹性联接的双质量(惯量)伺服系统，要求： 1）以电动机电枢电压 ua 为输入、负载角位移θL 为输出，建立系统的传递 函数模型； 2）画出系统动态结构图； 3）参考下列参数值，对系统的单位阶跃响应进行仿真。 La=0.001; Ra=1.0; Ki=0.001; Jm=0.005; bm=0.010; km=10; Ce=0.001; JL=0.15; bL=8.0; KL=5.0; %L<<1, Inductance of motor armature % Resistance of motor armature % Current feedback coefficient % Equivalent moment of inertia of motor % Viscosity damp coefficient of motor % Motor moment coefficient % Voltage feedback coefficient % Equivalent moment of inertia of frame % Viscosity damp coefficient of frame % Motor moment coefficient between frame & motor 图 1.1 弹性联接的双质量(惯量)伺服系统 1.1 建模方法综述 1.1.1 传递函数 先根据物理原理建立机电系统各部分的微分方程，然后进行拉氏变换，作出 各部分的动态结构图，再将各个部分连接起来，得到总体传递函数。
    1.1.2 状态空间方程 先选取合适的状态变量，根据传递函数列出状态方程和输出方程。 1.2 建模分析 1.2.1 系统建模过程 系统建模的一般步骤： （1）根据物理原理建立系统各个部分的微分方程，将各部分连接起来，得 到总体传递函数。 根据上面的分析并忽略轴的转动惯量，可以列出整个系统的电学方程以及动 力学方程： 电动机: 负载:  u C a e  d  m dt di dt i R a a  L a T m i k a m 2 dJ  m 2 d t m  T m  K (   m L  ) L T mL  J L 2 d  L 2 d t K (   L m )  T mL L  0 (1.1) (1.2) (1.3) (1.4) (1.5) （2）将得到的微分方程进行拉氏变换，作出各部分的动态结构图，如图 1.2；
    （3）建立从电枢电压 au 到 m 的传递函数模型 图 1.2 系统动态结构图 假设系统初始状态为 0，对整个系统电学及动力学方程，做拉氏变换可得  m ( ) s a  ( )  ( ) ( ) L sI s U s C s R I s   a a e  ( ) ( ) T s k I s   m m  2 ( ) T s K J s s    m m m  2 ( ) T s J s    L mL L  ( ( )) ( ) K s s     L m (  m T mL ( ) ( ) s   L L ( ) s   L ( )) s （1.6） 根据图 1.2 电机-负载模型方框图，利用梅森公式可得从 au 到 m 的传递函数  G s ,   G s    s  m   U s a  k m  L s R a a  1 J s m (1    1 s  1 J s L   1 s K L ) （1.7） 其中， 1       k m  L s R a a k m  L s R a a    1 J s m 1 J s m 1 J s m 1 J s L 1 s  C e    1 s K L  1 J s L   1 s K L     C e    K L （4）求出从 m 到 L 的传递函数模型，并求其频率特性和根轨迹 由方程组（1.6）的最后两个等式经过化简可得从 m 到 L 的传递函数模型：   G s   L  m   s   s  K L 2  J s L K L （1.8）
    1.2.2 Matlab 仿真 1 0.15s+0.001 Ua step E 10 0.001s+1 1 0.005s+0.001 -K- Ce Scope 1 s kL 5 1 s 【作业二】 对如图所示机床伺服进给系统进行建模，要求： 1） 按建模步骤写出建模过程； 2） 画出动态结构图； 3） 以位置指令为输入、工作台位置为输出，求出系统闭环传递函数； 4） 求出状态空间表达式； 5） 分析该系统的工作原理及其动态性能主要影响因素； 6） 对系统的阶跃响应和频率特性进行仿真（选做）。
    位置指令 + 脉冲 Pp Pe D/A Ve K1 ＞ Vc Va ﹣ PL ﹣ Vg Ka ＞ Kf VM KM DC 电机 K3 XL Kp 图 2.1 机床伺服进给系统、 2.1 建模方法综述 2.1.1 传递函数 先根据物理原理建立机电系统各部分的微分方程，然后进行拉氏变换，作出 各部分的动态结构图，再将各个部分连接起来，得到总体传递函数。 2.1.2 状态空间方程 先选取合适的状态变量，根据传递函数列出状态方程和输出方程。 2.2 建模分析 2.2.1 系统建模过程 系统建模的一般步骤为： (1) 根据物理原理建立系统各个部分的微分方程； (2) 将得到的微分方程进行拉氏变换，作出各部分的动态结构图； (3) 将各部分连接起来，得到总体传递函数。 分析整个机床伺服进给系统，直流伺服电机是其中最主要的组成部分，其原 理如图 2.2 所示。其中， au 表示电枢电压， aL 表示电枢电感， ai 表示电枢回路电 流， aR 表示电枢电阻， ae 表示电枢的反向电动势，T 表示电机产生的电磁转矩， LT 表示负载转矩， eu 表示位置偏差信号。
    图 2.2 直流电机原理图 建立直流电机部分的微分方程。 根据基尔霍夫电压定律： u a  L a di a dt  Ri a a  e a （2.1） 其中， ae 是电机电枢旋转时产生的反电势，大小磁通量、电机转速成正比， 方向与 au 相反，其计算表达式为： e a  dC  dt E amiCT  （2.2） （2.3） 其中， T i a 也称为电机的转矩系数。 考虑电机输出轴上的转矩平衡，电机的输入力矩与输出力矩相等，而输出力 矩主要由电机轴的旋转消耗、电机轴粘性摩擦消耗、负载消耗三部分组成。平衡 方程如下： T  2  2 dJ dt  dB  dt T L i （2.4） 其中 J 为电机轴的转动惯量， B 为电机轴的粘性摩擦系数，i 为减速器的传 动比。 对于负载部分（丝杠螺母传动），输入转矩与输出转矩平衡： T L  2 dJ  L 2 dt L  df  L dt L （2.5）
    分享到：
    赞 收藏

    相关推荐

    资料库

    课程资源

    共收录17145份资料，累计13个分类，关注成员有19位，主要包括：PHP,网络管理,网页制作,Java,.Net,数据库,3G/移动开发,C/C++,游戏开发,嵌入式,讲义,软件测试,专业指导

    热门标签

    PHP 网络管理 网页制作 Java .Net 数据库 3G/移动开发 C/C++ 游戏开发 嵌入式 讲义 软件测试 专业指导

    最新资料