logo资料库

2022-2023学年广东省深圳市罗湖区九年级上学期数学期中试卷及答案.doc

发布时间：2023-10-14 发布人：admin 分类：说明书 资料大小：1.54M 资料格式：doc 举报 版权申诉
第1页 / 共18页
第2页 / 共18页
第3页 / 共18页
第4页 / 共18页
第5页 / 共18页
第6页 / 共18页
第7页 / 共18页
第8页 / 共18页
资料共18页，剩余部分请下载后查看
    2022-2023 学年广东省深圳市罗湖区九年级上学期数学期中 试卷及答案 一、选择题（共 10 小题，每小题 3 分） 1. 下列方程是一元二次方程的是（ ） A. x   1 0 B. 2 2x  2 1 5 x   【答案】D 【解析】 C. 1 x  4 D. 【分析】根据一元二次方程的概念，对选项逐个判断即可．含有一个未知数并且未知数的次 数为 2 的整式方程为一元二次方程． 【详解】解：A、未知数的最高次数为 1，不是一元二次方程，不符合题意； B、是不等式，不是等式，不符合题意； C、分母有未知数，为分式方程，不符合题意； D、是一元二次方程，符合题意； 故选 D 【点睛】此题考查了一元二次方程的概念，解题的关键是掌握一元二次方程的概念． 2. 下列图形中，主视图为矩形的是（ ） A. C. 【答案】B 【解析】 B. D. 【分析】主视图是从物体的正面看得到的图形，分别写出每个选项中的主视图，即可得到答 案． 【详解】解：A．此几何体的主视图是等腰梯形； B．此几何体的主视图是矩形； C．此几何体的主视图是等腰梯形； D．此几何体的主视图是等腰三角形；
    故选：B． 【点睛】本题考查了三视图，三视图是指主视图，俯视图，左视图，其中：主视图是指从前 往后看到的平面图形；俯视图是指从上往下看到的平面图形；左视图是指从左往右看到的平 面图形． 3. 一元二次方程有两个不相等的实数根，则（ A. Δ 0 C. Δ 0＞ 【答案】C ） B. Δ 0＜ D. 与  的取值无关 【解析】 【分析】利用一元二次方程根的情况对应判别式的取值即可． 0  时，一元二次方程有两个不相同的实数根， 【详解】解：当 当 Δ 0 时，一元二次方程有两个相同的实数根， 当 Δ 0 时，一元二次方程没有实数根， 故选 C． 【点睛】本题主要考查一元二次方程根的情况与判别式的关系，能够熟记判别式是解题关键． 4. 如果点 (1,2) P 在双曲线 y  上，那么 k 的值是（ k x ） A. 4 【答案】C 【解析】 B. 4 C. 2 D. 2 【分析】根据点 (1,2) P 在双曲线 y  上可得， 2 k x k ，则可得 2 1 k  ． 【详解】解：由题意可得 2 k ，则 2 k  1 故选：C 【点睛】此题考查反比例函数图像上点的坐标特征，将点坐标代入函数解析式是解题关键． 5. 小张抛掷两枚质地均匀的硬币，出现两枚硬币全部正面朝上的概率是（ ） A. 1 4 【答案】A 【解析】 B. 1 2 C. 3 4 D. 1 【分析】采用树状图法列举即可求解． 【详解】画树状图为：
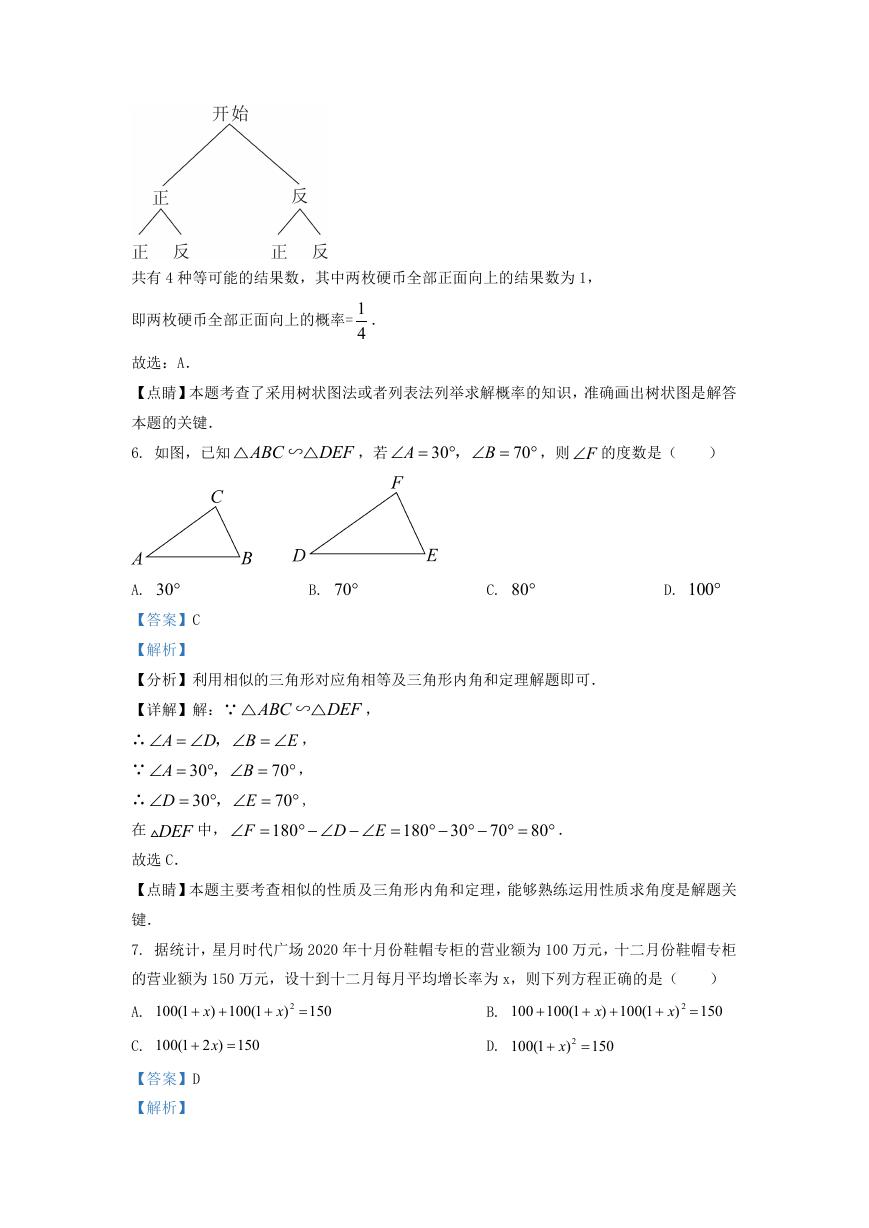
    共有 4 种等可能的结果数，其中两枚硬币全部正面向上的结果数为 1， 即两枚硬币全部正面向上的概率= 1 4 ． 故选：A． 【点睛】本题考查了采用树状图法或者列表法列举求解概率的知识，准确画出树状图是解答 本题的关键． 6. 如图，已知 ABC △ A. 30 【答案】C 【解析】 ∽ △ DEF ，若   A 30    ， B 70  ，则 F 的度数是（ ） B. 70 C. 80 D. 100 △ DEF 【分析】利用相似的三角形对应角相等及三角形内角和定理解题即可． 【详解】解：∵ ABC △ ∽ B ∴ A E D       ， 70 30 A B       ， ， ∵ 70 30 E D       ， ∴ 180 F 在 DEF          中， 故选 C． 180  ．   80   30   70 D E ， ， , 【点睛】本题主要考查相似的性质及三角形内角和定理，能够熟练运用性质求角度是解题关 键． 7. 据统计，星月时代广场 2020 年十月份鞋帽专柜的营业额为 100 万元，十二月份鞋帽专柜 的营业额为 150 万元，设十到十二月每月平均增长率为 x，则下列方程正确的是（ ） A. 100(1  ) 100(1 x   2 ) x  150 B. 100 100(1   ) 100(1 x   2 ) x  150 C. 100(1 2 ) 150 x  【答案】D 【解析】 D. 100(1 ) x 2  150
    【分析】利用十二月份的营业额＝十月份的营业额×（1＋增长率）2，即可得出关于 x 的一 元二次方程，此题得解． 【详解】解：依题意得：100（1＋x）2＝150． 故选：D． 【点睛】本题考查了由实际问题抽象出一元二次方程，找准等量关系，正确列出一元二次方 程是解题的关键． 8. 若 1x  是关于 x 的一元二次方程 2 x mx  的一个根，则 m 的值是（ 0 ） A. 2 【答案】B B. 1 C. 1 D. 2 x mx 【解析】 【分析】把 1x  代入方程 2 【详解】解：∵ 1x  是关于 x 的一元二次方程 2 ∴ 21 解得： 0m 1 m   ．  ，  ，即可求解． 0 x mx  的一个根， 0 故选：B 【点睛】本题主要考查了一元二次方程的解的定义，熟练掌握能使方程左右两边同时成立的 未知数的值是方程的解是解题的关键． 9. 关于反比例函数 y  ，下列说法不正确的是（ 1 x ） A. 函数图象分别位于第二、四象限 C. 函数图象经过点 11， B. 函数图象关于原点成中心对称 D. 当 x＞0 时，y 随 x 的增大而减小 【答案】A 【解析】 【分析】根据反比例函数图象上点的坐标特征对 C 进行判断；根据反比例函数的性质对 A、 B、D 进行判断． 【详解】解：反比例函数 y  ， 1 0 k   ， 1 x A、函数图象分别位于第一、三象限，故本选项说法不正确，符合题意； B、函数图象关于原点成中心对称，故本选项说法正确，不符合题意； C、函数图象经过点 D、当 0 故本选项说法正确； 11， ，故本选项说法正确，不符合题意； k  ，双曲线的两支分别位于第一、三象限，在每一象限内 y 随 x 的增大而增小， 故选：A．
    【点睛】本题考查了反比例函数的性质：反比例函数 y  k x  k 0  的图象是双曲线；当 0k＞ ，双曲线的两支分别位于第一、第三象限，在每一象限内 y 随 x 的增大而减小；当 0k＜ ， 双曲线的两支分别位于第二、第四象限，在每一象限内 y 随 x 的增大而增大． 10. 边长为 4 的正方形 ABCD 中，对角线 AC，BD 交于点 O，E 在 BD 上，作 EF⊥CE 交 AB 于点 F，连接 CF 交 BD 于 H，则下列结论：①EF=EC；② 2=CF CG CA ；③ BE DH 16  ；,④ 若 BF=1，则 DE  3 2 2 ，正确的是（ ） B. ②③④ C. ①②③ D. A. ①②④ ①②③④ 【答案】D 【解析】 【分析】①由“ SAS ”可证 ADE △ 四边形的内角和定理可证 AFE   ②通过证明 FCG  ACF ∽  ，可得 2CF  ，可得 AE EF  ， DAE EC   DCE ，由 ； CDE  ，可得 AE EC △ BCE EAF    CG CA  ；  CH DH EC CD  ③ 通 过 证 明 ECH CDH ∽  ， 可 得 ， 通 过 证 明 ECH  ∽ EBC ， 可 得 CH BC EC BE  ，可得结论； ④通过证明 AFC △ ∽ △ D EC ，可得 【详解】如图，连接 AE ， AF AC DE CD  ，即可求解．
    CDB   BAC   DAC  45  ， ， ，   DCE ，   BCE  360  ， ，  ，  ADB      45 45 ，           EFB   180  ，  180   ， EAF   FEC ， ECF  EFC  FCG   ACF ，  四边形 ABCD 是正方形， AD CD     ， 又 DE DE  ， (SAS) CDE ADE     AE EC ， DAE    BCE EAF  FEC ABC   BCE EFB  BFE AFE   又 AFE BCE  AE EF   ， EF EC   ，故①正确； EF EC 90 EFC  ，  FAC   ， 又 ACF   FCG  ∽ CA  CF CG CF 2CF   ECH   ECH  ∽  CH EC DH CD  CH DH EC CD ECH     ECH  ∽  CH EC BE  CH BC BE  DH BC CD BE DBC ， EBC BC EC ， ，     ， ，  ， ，  CG CA    ，故②正确； ， EHC CDB CDH ，    DHC ， ， BEC    CEH ，
    16  ，故③正确； ， ，  ， BC CD DH BE     4 AB  ， BF   AF 4 2 AC  45 ACD     DCE       1 3 ECF ACF  AFC ， CDE DEC ， 又 FAC   △ ∽△  AF AC DE CD ，  ，  45  ，  3 DE  ， 2  DE ，故④正确， 3 2 2 故选： D ． 【点睛】本题是四边形综合题，考查了全等三角形的判定和性质，正方形的性质，相似三角 形的判定和性质，灵活运用这些性质解决问题是本题的关键． 二、填空题（共 5 小题，每小题 3 分） 11. 一元二次方程 2 x  的根是 1x  _______， 2x  _______ 4 【答案】 ①. 2 ②. -2 【解析】 【分析】把方程两边同时开方，即可得到结论． 2 【详解】∵ 2 x  或 2 4 x  ， 2 x   ， ∴ 1 故答案为：2， 2 ． 【点睛】本题考查了解一元二次方程-直接开平方法，正确掌握解一元二次方程的方法是解 题的关键． 12. 若3 x y ，则 2 x y  __________. 【答案】 2 3 【解析】 【分析】根据等式的基本性质，将等式的两边同时除以3y ，即可得出结论. 【详解】解：将等式的两边同时除以3y ，得 x y  2 3
    故答案为： 2 3 . 【点睛】此题考查的是将等式变形，掌握等式的基本性质是解决此题的关键. 13. 一个不透明的口袋中有红球和黑球共若干个，这些球除颜色外都相同．每次摸出 1 个球， 进行大量的摸球试验后，发现摸到黑球的频率在 0.4 附近摆动，据此估计摸到红球的概率约 为______． 【答案】0.6（ 【解析】 3 5 或 60%） 【分析】根据题意，首先求得摸到黑球的概率，然后求得摸到红球的概率即可． 【详解】解：∵每次摸出 1 个球，进行大量的球试验后，发现摸到黑球的频率在 0.4 附近摆 动， ∴摸到黑球的概率约为 0.4， ∴摸到红球的概率约为 1-0.4=0.6， 故答案为：0.6． 【点睛】本题考查用样本估计总体，解答本题的关键是明确题意，求出黑球的个数． 14. 如图是小孔成像原理的示意图， , 高度为15cm ，则像 CD 的高度是_________ cm ． OA  30cm OC  10cm ， AB CD ．若物体 AB 的 【答案】5 ， 则 有 ABO CDO ∽  ， 则 有  30 10  ， AB 高度已知，即可求出CD ． 【解析】 【 分 析 】 根 据 小 孔 成 像 的 原 理 ， 因 为 AB CD AB OA CD OC 【详解】解： AB CD  ABO CDO 30 10 ，  ∽ AB OA CD OC AB   ，  ，   ， 3 15cm ， 又 CD  故答案为：5． 5cm 【点睛】本题考查了相似三角形的应用，相似比对应高度之比在相似中用的比较广泛，解决
    分享到：
    赞 收藏

    相关推荐

    资料库

    初中三年级

    共收录1452份资料，累计55个分类，关注成员有19位，主要包括：2023年,2022年,2021年,2020年,辽宁,2024年,湖北,福建,2019年,四川,湖南,浙江,河北,天津,江苏,上海,广东,北京

    热门标签

    2023年 2022年 2021年 2020年 辽宁 2024年 湖北 福建 2019年 四川 湖南 浙江 河北 天津 江苏 上海 广东 北京

    最新资料