logo资料库

Apriori算法及改进算法分析.doc

发布时间：2022-06-09 发布人：admin 分类：说明书 资料大小：0.48M 资料格式：doc 举报 版权申诉
第1页 / 共7页
第2页 / 共7页
第3页 / 共7页
第4页 / 共7页
第5页 / 共7页
第6页 / 共7页
第7页 / 共7页
资料共7页，全文预览结束
    山西大学研究生学位课程论文 （2014 ---- 2015 学年 第 2 学期） 学院（中心、所）： 计算机与信息技术学院 专 业 名 称： 计算机应用技术 课 程 名 称： 数据挖掘 论 文 题 目： Apriori 算法及改进算法分析 授课 教师（职称）： 研 究 生 姓 名： 年 学 成 级： 号： 绩： 评 阅 日 期： 山西大学研究生学院 2015 年 6 月 2 日 Apriori 算法及改进算法分析 摘要 随着大数据，云时代的来临，我们每天面临越来越多数据并且每天都在产生大量的新数据。 然而我们却遭遇着数据过量，知识匮乏的困境。这就需要我们对数据进行挖掘，提取有效的知 识来帮助我们进行决策等实际生产工作。其中关联规则模型是数据挖掘中的重要方法。Apriori
    算法是最具有代表性的经典算法。本文介绍了 Apriori 算法的基本原理，及其一些算法改进的 思路。 关键词 数据挖掘；关联规则；Apriori 1.引言 随着大数据，云时代的来临，各行各业都积累了大量的数据，并且每天仍在产生着大量的 新数据。如何快速、准确、方便地从海量的信息库中获取重要的，隐含在数据中的，未知但是 潜在有用的信息，模式或知识，已成为人们亟待解决的问题。其中关联规则反应一个事物与其 他事物之间的相互依存性和关联性，如果如果两个或者多个事物之间存在一定的关联关系，那 么，其中一个事物就能够通过其他事物预测到。 1993年，IBM公司Almaden研究中心的R.Agrawal等人首先在SIGMOD会议上提出关联规则模 型，并给出求解算法AIS。随后又出现了SETM和Apriori等算法。其中，Apriori是关联规则模型 中的经典算法。 2.关联规则模型 关联规则就是借助数据挖掘的技术从数据库中分析和提取出高频数据项，进而挖掘出项组 之间存在的关系规则，以实现对资源的有效利用，在实际应用领域得到了广泛的应用。关联规 则算法也是一直地推算法，在计算过程中以贫集地推思想实现两个阶段的计算流程：第一步寻 找出数据信息中的全部频集，根据原先设定好的最小支持度，找出所有的频繁项集。第二步有 频繁项集产生强关联规则，即找到满足最小支持度和最小置信度的关联规则。第二步是容易实 现的，所以关联规则挖掘算法的性能主要体现在第一步。 2.1 关联规则模型基本概念 设 I={i1, i2,…, im}为所有项目的集合，D 为事务数据集，事务 T 是一个项目子集（T I）。 每一个事务具有唯一的事务标识 TID。设 A 是一个由项构成的集合，称为项集。事务 T 包含项 集 A，当且仅当 A T。如果项集 A 中包含 k 个项，则称其为 k 项集，即 X={x1，x2..xk}。 如果项集的支持度超过用户给定的最小支持度阈值，就称该项集是频繁项集（或大项集）。 关联规则：如果 AB 都是 I 的子集，且 AB 没有交集，出现 A 的时候也出现 B 就说 AB 相互关 联。 支持度 s：项集 A 和 B 在事务数据库 D 中出现的次数占 D 中总事务的比值。 可信度 c：D 中同时包含 A 和 B 的事务数与只包含 A 的事务数的比值
    关联规则标准: 最小支持度 – 表示规则中的所有项在事务中出现的频度 最小可信度 - 表示规则中左边的项(集)的出现暗示着右边的项(集)出现的频度 强规则： 通常定义为那些满足最小支持度和最小可信度的规则. 2.2 关联规则挖掘步骤 1）通过事先设定的 最小支持度（min-sup），找出所有的频繁项集，即找出支持度大于或 等于给定的最小支持度阈值的所有项集，从而递归查找 1 到 k 的频繁项集。 2）由频繁项集产生强关联规则，即找到满足最小支持度（min-sup）和最小置信度（min-conf） 的关联规则。 3.Apriori 算法及改进算法 3.1Apriori 算法 3.1.1 基本概念 Apriori 算法是一种经典的生成布尔型关联规则的频繁项集挖掘算法.算法名字是缘于算 法使用了频繁项集的性质这一先验知识. Apriori 性质：频繁项集的子集必为频繁项集，非频繁项集的超集一定是非频繁的。 Apriori 剪枝原理: 若任一项集是不频繁的,则其超集不应该被生成。 思想: Apriori 使用了一种称作 level-wise 搜索的迭代方法,其中 k-项集被用作寻找 (k+1)-项集，用候选项集 Ck 找频繁项集 Lk。 首先,找出频繁 1-项集, 以 L1 表示。L1 用来寻 找 L2, 即频繁 2-项集的集合。L2 用来寻找 L3, 以此类推,直至没有新的频繁 k-项集被发现。每 个 Lk 都要求对数据库作一次完全扫描，每次都剪除不满足最小支持度的候选项集。 3.1.2 算法描述： (1 ) 首次扫描数据集生成候选集 C1 ， 通过逐层扫描统计候选集中每个项集 X 的支持 度， 删除 X． support＜ minsupport 的项集得到频繁集 L1 ; (2) 频繁集 L1 再进行自身连接生成候选集 C2 ， 再次通过逐层扫描， 删除 X． support ＜ minsupport 的项集得到频繁集 L2 ; (3 ) 对 k ≥ 2 的每个候选集 Ck ， 重复第 2 步， 最终得出最大频繁项集 Lk 。 Apriori 算法实例如图 1：
    图 1Apriori 算法实例 3.2Apriori 算法改进分析 3.2.1 主要问题及思路 算法改进的关键问题是减少 Apriori 算法扫描次数及候选集的数量。 改进思路主要体现在以下三个方面： （1）剪枝步的算法改进，通过连接 Apriori 算法生成了候选项集，并对候选项集全部子集 进行频繁集判断，然后剪枝以降低过程中的负荷，从而有助于候选项集生成速度的提高。 （2）程序改进，转化数据表中的数据，使之成为二维数组中的数据，则不需要在数据库中 进行各数据的记录、搜索和判断，候选项集判断是否符合频繁项集要求的效率显著提高，从而 进一步促进程序运行效率的提高。 （3）在产生 k- 项频繁项集后，去掉一些非频繁项集，以免再次组合成候选项。去掉某些 特殊的事务记录，它们在产生（k+1）-项频繁项集时不再被考虑计数问题。简化的过程类似于 在矩阵中逐步去掉行和列，从而拓宽存储空间，以实现数据读取速度、算法运行效率的提高。 3.2.2 基于减少数据库扫描的 Apriori 改进方法 首先，对数据库进行一次全面扫描，确定记录数量并对记录进行排序，然后在生成候选集 C1 的同时，删除事务集中不支持 L1 的事务以及事务中的项目； 第 3 步是对数据库中项目集进行二进制编码，编码的长度为记录数量，项目在事务集的某个记 录中出现时用“1”表示，没有出现时则用“0”表示； 第 4 步是将得到的编码表进行转置，生成关于项集编码的表格，并对关于项集 Ii 编码中“1” 的个数进行累加计数，由给定的最小支持度与“1” 的计数进行比较，若 count（1） ≥ min-sup， 则得到的为频繁 1-项集；
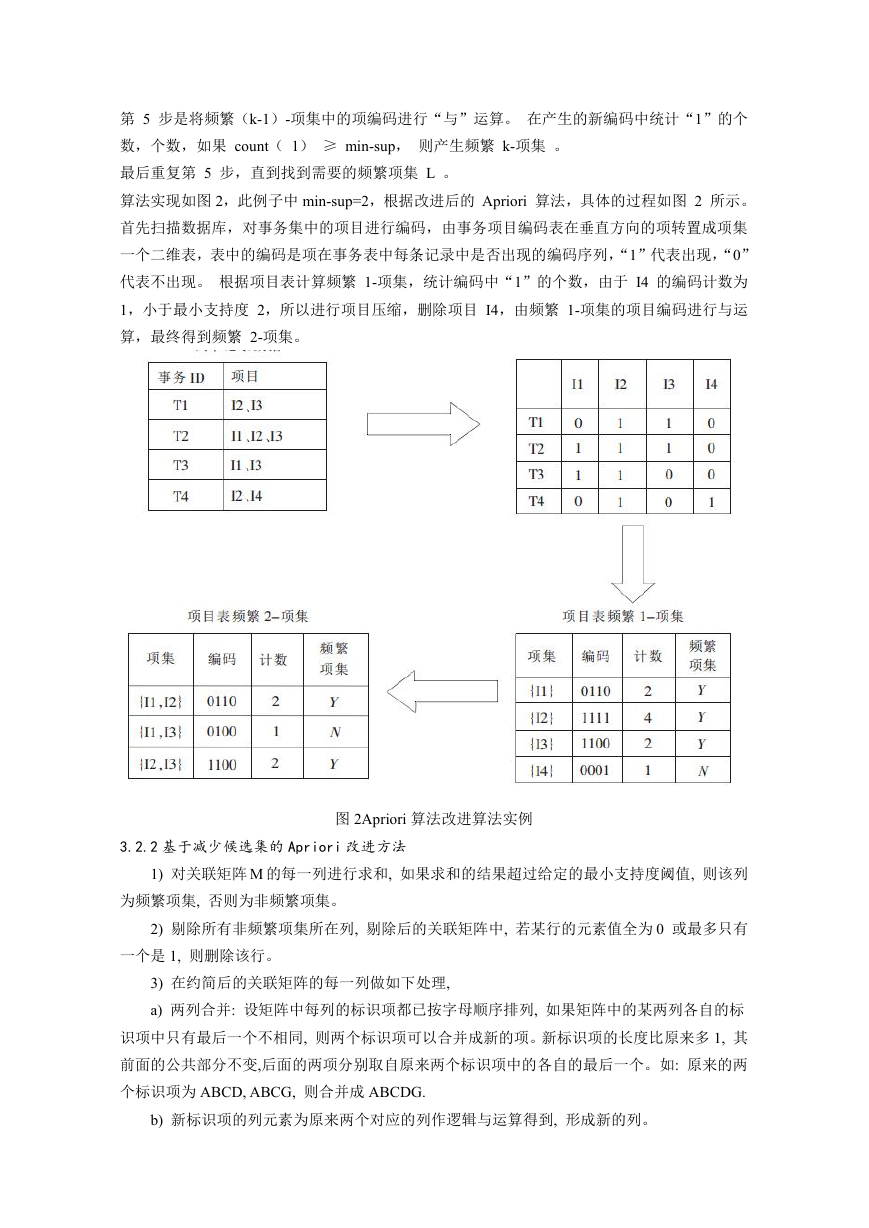
    第 5 步是将频繁（k-1）-项集中的项编码进行“与”运算。 在产生的新编码中统计“1”的个 数，个数，如果 count（ 1） ≥ min-sup， 则产生频繁 k-项集 。 最后重复第 5 步，直到找到需要的频繁项集 L 。 算法实现如图 2，此例子中 min-sup=2，根据改进后的 Apriori 算法，具体的过程如图 2 所示。 首先扫描数据库，对事务集中的项目进行编码，由事务项目编码表在垂直方向的项转置成项集 一个二维表，表中的编码是项在事务表中每条记录中是否出现的编码序列，“1”代表出现，“0” 代表不出现。 根据项目表计算频繁 1-项集，统计编码中“1”的个数，由于 I4 的编码计数为 1，小于最小支持度 2，所以进行项目压缩，删除项目 I4，由频繁 1-项集的项目编码进行与运 算，最终得到频繁 2-项集。 3.2.2 基于减少候选集的 Apriori 改进方法 图 2Apriori 算法改进算法实例 1) 对关联矩阵 M 的每一列进行求和, 如果求和的结果超过给定的最小支持度阈值, 则该列 为频繁项集, 否则为非频繁项集。 2) 剔除所有非频繁项集所在列, 剔除后的关联矩阵中, 若某行的元素值全为 0 或最多只有 一个是 1, 则删除该行。 3) 在约简后的关联矩阵的每一列做如下处理, a) 两列合并: 设矩阵中每列的标识项都已按字母顺序排列, 如果矩阵中的某两列各自的标 识项中只有最后一个不相同, 则两个标识项可以合并成新的项。新标识项的长度比原来多 1, 其 前面的公共部分不变,后面的两项分别取自原来两个标识项中的各自的最后一个。如: 原来的两 个标识项为 ABCD, ABCG, 则合并成 ABCDG. b) 新标识项的列元素为原来两个对应的列作逻辑与运算得到, 形成新的列。
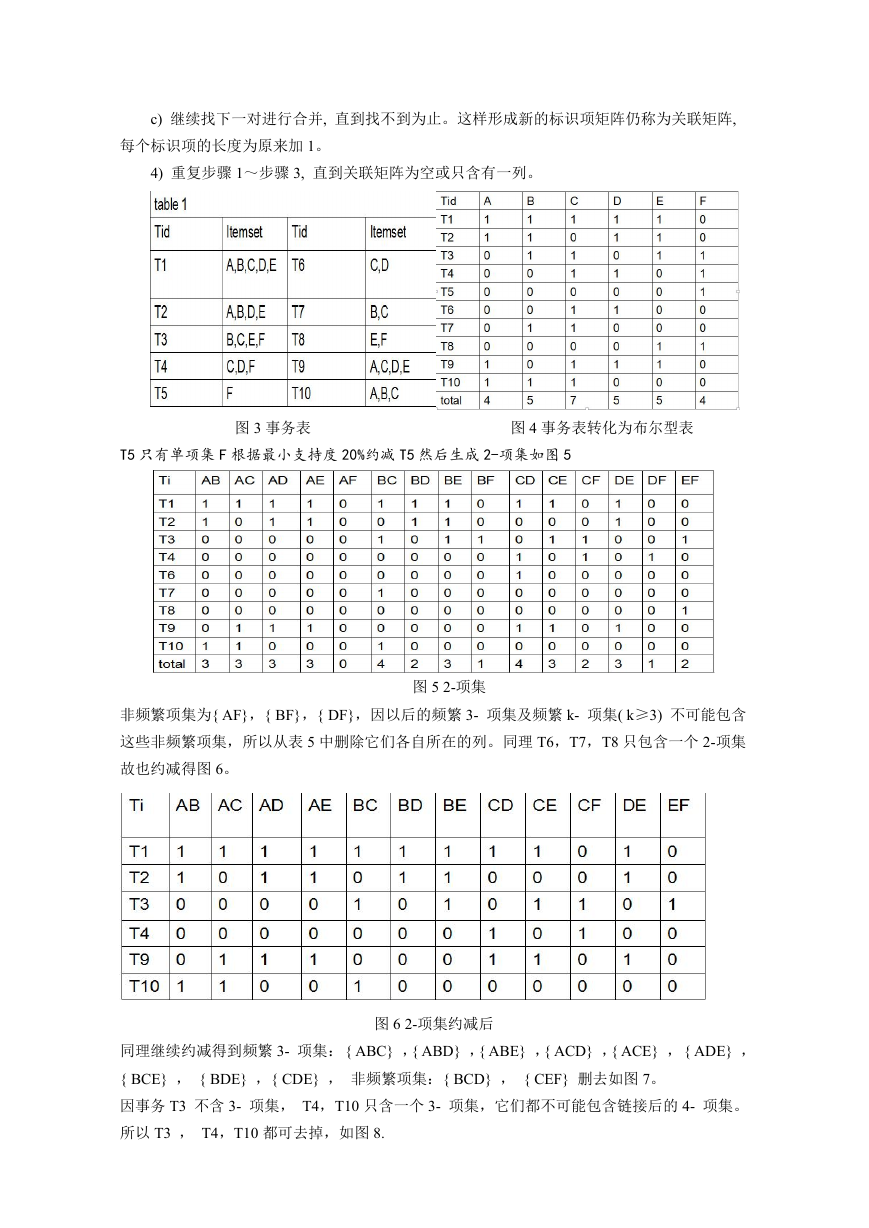
    c) 继续找下一对进行合并, 直到找不到为止。这样形成新的标识项矩阵仍称为关联矩阵, 每个标识项的长度为原来加 1。 4) 重复步骤 1～步骤 3, 直到关联矩阵为空或只含有一列。 图 3 事务表 图 4 事务表转化为布尔型表 T5 只有单项集 F 根据最小支持度 20%约减 T5 然后生成 2-项集如图 5 图 5 2-项集 非频繁项集为{ AF}，{ BF}，{ DF}，因以后的频繁 3- 项集及频繁 k- 项集( k≥3) 不可能包含 这些非频繁项集，所以从表 5 中删除它们各自所在的列。同理 T6，T7，T8 只包含一个 2-项集 故也约减得图 6。 图 6 2-项集约减后 同理继续约减得到频繁 3- 项集：{ ABC} ，{ ABD} ，{ ABE} ，{ ACD} ，{ ACE} ，{ ADE} ， { BCE} ， { BDE} ，{ CDE} ， 非频繁项集：{ BCD} ， { CEF} 删去如图 7。 因事务 T3 不含 3- 项集， T4，T10 只含一个 3- 项集，它们都不可能包含链接后的 4- 项集。 所以 T3 ， T4，T10 都可去掉，如图 8.
    图 7 图 8 继续进行约减 得到频繁 4 – 项集：{ ABDE} ，{ ACDE} 。去掉非频繁项：{ ABCE} 。约简 事务： 去掉 T2，T9，它们只包含一项 4- 项集，同理可删除掉。因 ABDE 和 ACDE 无法链接 成 5- 项集，所以频繁 5- 项集为空。最后得到频繁 4- 项集：{ ABDE}，{ ACDE} ， 所有的频 繁集是它们的所有子集。最终结果如图 9 4.总结 图 9 基于减少数据库扫描的改进算法在第 1 步扫描数据库并对每个项目编码，后续的过程都是 针对编码进行“与”运算，不需要对数据库进行重复扫描。 同时由于删除了小于最小支持度的 项以及含有该项目的事务，可以有效地减小系统的开销，从而提高挖掘效率。 基于减少候选集的改进算法操作关联矩阵在行向量既表示每条事务所含的项目, 也蕴涵了 事务的相似性；列向量既反映了每个项在事务中的访问情况, 也蕴涵了列之间的相似性,可以很 快约减候选集从而提高算法效率。 参考文献 [1] 刘自然，王律强等．改进 Apriori 算法对试车台监测数据的关联挖掘．中国测试，2015,41(4): 106-109 [2] 孙福兆．改进型 Apriori 算法在学生管理系统中的应用研究．软件导刊，2015，14(3)：59-60 [3] 吴红星，王浩．基于 Apriori 改进算法的企业 Web 日志挖掘研究．计算机科学与发展，2015， 25(4)：43—47 [4] 田伟．基于数据挖掘的高校学生成绩分析与管理．牡丹江教育学院学报，2015，3：99-101 [5] 刘帅，杨英杰等．改进的模糊关联规则及其挖掘算法．计算机工程与设计，2015，36(4)： 942-946 [6] 陈凤娟．面向数据流的频繁项集挖掘．洛阳师范学院学报，2015，34(2)：82-85 [7] 杜焕强，俞立封．一种高效的关联规则连续增量更新改进算法．哈尔滨师范大学自然科学 学报，2015，31(3)：49-52
    分享到：
    赞 收藏

    相关推荐

    资料库

    课程资源

    共收录17145份资料，累计13个分类，关注成员有19位，主要包括：PHP,网络管理,网页制作,Java,.Net,数据库,3G/移动开发,C/C++,游戏开发,嵌入式,讲义,软件测试,专业指导

    热门标签

    PHP 网络管理 网页制作 Java .Net 数据库 3G/移动开发 C/C++ 游戏开发 嵌入式 讲义 软件测试 专业指导

    最新资料