MATLAB图像大作业.pdf-资料库

图像大作业第一部分基础知识 2.相关程序如下 close all,clear all, clc; load('hall.mat'); T=hall_color; for count=1:120 for count2=1:168 if((count-60)^2+(count2-84)^2<=3600) T(count,count2,1)=255; T(count,count2,2)=0; T(count,count2,3)=0; end end end image(T); imwrite(T,'TI1.bmp','bmp'); 效果为 close all, clear all, clc; load('hall.mat'); T=hall_color; for count=1:8 for count2=1:8 if(mod(count+count2,2)==0) T((count-1)*15+1:count*15,(count2-1)*21+1:count2*21,1)=0; T((count-1)*15+1:count*15,(count2-1)*21+1:count2*21,2)=0; T((count-1)*15+1:count*15,(count2-1)*21+1:count2*21,3)=0; end end end image(T); imwrite(T,'T2.bmp','bmp');

效果为第二部分图像压缩编码 1. 图像的预处理是将每个像素灰度值减去 128 ，这个步骤是否可以在变换域进行？请在测试图像中截取一块验证你的结论。这个步骤是完全可行的。相关程序如下 clear all ,close all,clc; load('JpegCoeff.mat'); load('hall.mat'); example=double(hall_gray(1:10,1:10)); sub=ones(10,10)*128; dir=example-sub; indir=idct2(dct2(example)-dct2(sub)); ans=dir-indir; 我们得到ans中最大的绝对值为1.136868377216160e-13，基本可以忽略不计，所以我们可以知道，这个步骤是完全可行的。 2. 请编程实现二维DCT，并和MATLAB自带的库函数dct2 比较是否一致相关程序如下 clear all, close all, clc; load('hall.mat'); example=double(hall_gray(1:10,1:10)); %下为计算差别 difference=dct2(example)-mydct(example); example2=double(hall_gray(1:10,1:20)); answ=dct2(example2); function [back] = mydct(example) [x y]=size(example); D=zeros(x,y); for h=1:x for l=1:y if h==1 D(h,l)=sqrt(1/x); else D(h,l)=sqrt(2/x)*cos((h-1)*(2*l-1)*pi/(2*x));

end end end back=D*example*D'; end 得到的difference最大值为1.232902668846236e-12，可以忽略不计，所以两者功能基本相同，只不过库函数可以计算非方阵的矩阵。 3. 如果将DCT 系数矩阵中右侧四列的系数全部置零，逆变换后的图像会发生什么变化？选取一块图验证你的结论。如果左侧的四列置零呢？相关程序如下 clear all ,close all,clc; load('JpegCoeff.mat'); load('hall.mat'); middle=dct2(double(hall_gray)-ones(size(hall_gray))*128); [x y]=size(middle); middle1=[zeros(x,4),middle(:,(5:y))]; middle2=[middle(:,(1:(y-4))),zeros(x,4)]; transform=idct2(middle)+ones(size(middle))*128; transform1=idct2(middle1)+ones(size(middle))*128; transform2=idct2(middle2)+ones(size(middle))*128; figure; imshow(uint8(transform)); figure; imshow(uint8(transform1)); figure; imshow(uint8(transform2)); 左侧置零后图像，明显变灰右侧置零后图像，没有太大改变

出现上述情况的原因是，dct变换后左侧有很多直流分量，置零后，会使图像像128靠近，所以会变灰，而右侧较多高频分量，置零后，虽然会减少图像的高频分量，但人眼对高频分量并不敏感，所以会感觉图像变化不大。 4. 若对DCT 系数分别做转置、旋转90 度和旋转180 度操作(rot90) ，逆变换后恢复的图像有何变化？选取一块图验证你的结论。相关程序如下 clear all, close all, clc; load('hall.mat'); middle=dct2(double(hall_gray)-128); middle1=rot90(middle); middle2=rot90(middle,2); tt=idct2(middle)+128; transform=idct2(middle')+128; transform1=idct2(middle1)+128; transform2=idct2(middle2)+128; figure; imshow(uint8(transform)); figure; imshow(uint8(transform1)); figure; imshow(uint8(transform2)); 得到如下结果转置

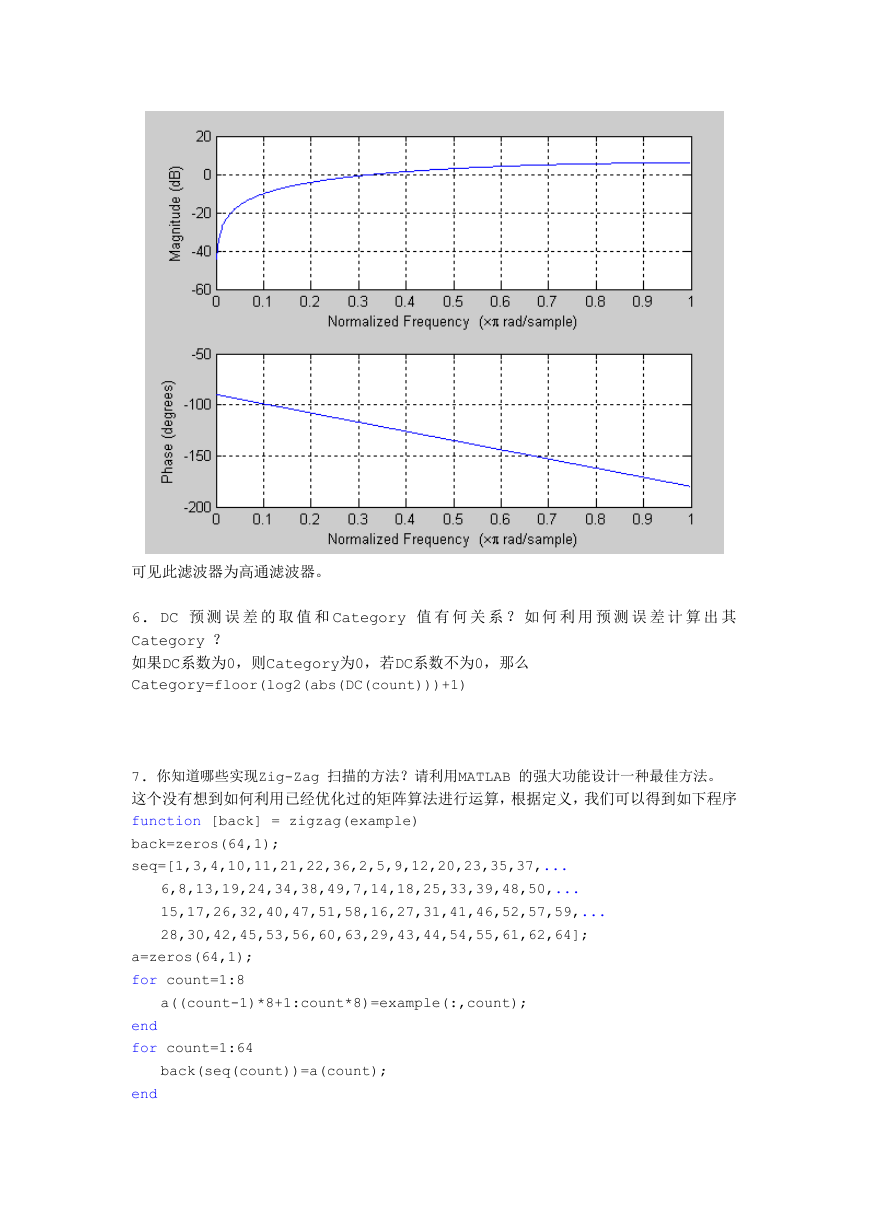
旋转90 旋转180 5. 如果认为差分编码是一个系统，请绘出这个系统的频率响应，说明它是一个高通滤波器。 DC 系数先进行差分编码再进行熵编码，说明DC 系数的高频频率分量更多相关程序为 clear all,close all, clc; freqz([-1 1],1); 我们得到这个滤波器的频率响应如下

可见此滤波器为高通滤波器。 6. DC 预测误差的取值和 Category 值有何关系？如何利用预测误差计算出其 Category ？如果DC系数为0，则Category为0，若DC系数不为0，那么 Category=floor(log2(abs(DC(count)))+1) 7. 你知道哪些实现Zig-Zag 扫描的方法？请利用MATLAB 的强大功能设计一种最佳方法。这个没有想到如何利用已经优化过的矩阵算法进行运算，根据定义，我们可以得到如下程序 function [back] = zigzag(example) back=zeros(64,1); seq=[1,3,4,10,11,21,22,36,2,5,9,12,20,23,35,37,... 6,8,13,19,24,34,38,49,7,14,18,25,33,39,48,50,... 15,17,26,32,40,47,51,58,16,27,31,41,46,52,57,59,... 28,30,42,45,53,56,60,63,29,43,44,54,55,61,62,64]; a=zeros(64,1); for count=1:8 a((count-1)*8+1:count*8)=example(:,count); end for count=1:64 back(seq(count))=a(count); end

end 以及逆zigzag程序 function [back] = inv_zigzag(example) back=zeros(8,8); seq=[1,3,4,10,11,21,22,36,2,5,9,12,20,23,35,37,... 6,8,13,19,24,34,38,49,7,14,18,25,33,39,48,50,... 15,17,26,32,40,47,51,58,16,27,31,41,46,52,57,59,... 28,30,42,45,53,56,60,63,29,43,44,54,55,61,62,64]; middle=zeros(64,1); for count=1:64 middle(count)=example(seq(count)); end for count=1:8 back(:,count)=middle((count-1)*8+1:count*8); end 8. 对测试图像分块、DCT 和量化，将量化后的系数写成矩阵的形式，其中每一列为一个块的DCT系数Zig-Zag扫描后形成的列矢量，第一行为各个块的DC系数。相关程序如下 clear all, close all, clc; load('JpegCoeff.mat'); load hall.mat hall_gray; [h l]=size(hall_gray); h=8*ceil(h/8); l=8*ceil(l/8); %若图像横纵不为8的倍数，则要补全 example=zeros(h,l); [h l]=size(hall_gray); example(1:h,1:l)=hall_gray; example=double(example)-128; answer=zeros(64,ceil(h/8)*ceil(l/8)); for count=1:ceil(h/8) for count2=1:ceil(l/8) answer(:,(count-1)*ceil(l/8)+count2)=... zigzag(round((dct2(example((count-1)*8+1:count*8,(count2-1)*8+1:count 2*8))./QTAB))); end end 9. 请实现本章介绍的JPEG 编码（不包括写JFIF 文件），输出为DC 系数的码流、AC 系数的码流、图像高度和图像宽度，将这四个变量写入jpegcodes.mat 文件。相关程序如下

T2_8 [h l]=size(answer); DC=answer(1,:); %差分运算如下 for count=2:l DC(count)=answer(1,count-1)-answer(1,count); end DCCode=[]; for count=1:l %找出cate，确定huff编码 if DC(count)==0 cate=1; else cate=floor(log2(abs(DC(count)))+2); end huff=DCTAB(cate,2:DCTAB(cate,1)+1); coo=trans(DC(count)); DCCode=[DCCode huff coo]; end DCCode=logical(DCCode); ACCode=[]; AC=answer(2:64,:); for count2=1:l run=0; last=find(AC(:,count2)~=0, 1, 'last' ); for count=1:last if AC(count,count2)==0 if run>=15 ACCode=[ACCode 1 1 1 1 1 1 1 1 0 0 1]; run=0; else run=run+1; end else %找出huff编码 if AC(count,count2)==-1||AC(count,count2)==1 cate=1; else cate=floor(log2(abs(AC(count,count2)))+1); end coo=trans(AC(count,count2)); ACCode=[ACCode ACTAB(run*10+cate,4:ACTAB(run*10+cate,3)+3)... coo];

资料库

MATLAB图像大作业.pdf

相关推荐

考试认证

热门标签

最新资料