2020-2021学年广西玉林市博白县八年级下学期期中数学试题及答案.doc-资料库

2020-2021学年广西玉林市博白县八年级下学期期中数学试题及答案.doc.pdf-第1页.jpg

第1页 / 共8页

2020-2021学年广西玉林市博白县八年级下学期期中数学试题及答案.doc.pdf-第2页.jpg

第2页 / 共8页

2020-2021学年广西玉林市博白县八年级下学期期中数学试题及答案.doc.pdf-第3页.jpg

第3页 / 共8页

2020-2021学年广西玉林市博白县八年级下学期期中数学试题及答案.doc.pdf-第4页.jpg

第4页 / 共8页

2020-2021学年广西玉林市博白县八年级下学期期中数学试题及答案.doc.pdf-第5页.jpg

第5页 / 共8页

2020-2021学年广西玉林市博白县八年级下学期期中数学试题及答案.doc.pdf-第6页.jpg

第6页 / 共8页

2020-2021学年广西玉林市博白县八年级下学期期中数学试题及答案.doc.pdf-第7页.jpg

第7页 / 共8页

2020-2021学年广西玉林市博白县八年级下学期期中数学试题及答案.doc.pdf-第8页.jpg

第8页 / 共8页

2020-2021 学年广西玉林市博白县八年级下学期期中数学试题及答案（全卷共三大题，共 4 页，满分 120 分，考试时间 120 分钟）注意事项: 1. 考生答题请将答案填写在答题卡上，在试卷上作答无效．考试结束，将答题卡交回． 2. 答选择题必须用 2B 铅笔把答题卡上对应题目的选项标号涂黑．如需改动，请用橡皮擦干净后，再选涂其他答案． 3. 答非选择题，用直径 0.5 毫米黑色墨水签字笔在答题卡指定的位置上，不在答题区域内的答案一律无效，不得用其他笔答题．一、选择题：（本大题共 12 小题，每小题 3 分，共 36 分）在每小题给出的四个选项中，只有一项是符合题目要求的，把正确答案的标号填（涂）在答题卡内相应的位置上． 1. 若式子 2x  在实数范围内有意义，则 x的取值范围是 A. x=－2 C. x＞－2 2. 以下列各组数为三边的三角形中不是直角三角形的是 B. x≥－2 D. x＜－2 A. 3，4，5 B. 13，5，12 C. 5，6，7 D. 41，40，9 3. 如图，在平行四边形 ABCD中，M是 BC延长线上的一点，若∠A=125°，则∠MCD的度数是 A .45° B. 75° C. 65° D. 55° 第 3 题图第 5 题图第 9 题图第 10 题图 4. 下列计算正确的是 A. 5 3 1 9 5. 如图，在平面直角坐标系中，点 P的坐标为 ( 2,3) 3 C. =5 B. 4 2 8   2  2 1 3 D. ( 3  2 2)   5 6  ，以点 O为圆心，OP的长为半径画弧，交 x轴的负半轴于点 A，则点 A的横坐标为 13 2  13 B.   A. C. 13 D. 2  13 6 . 我们把顺次连接任意一个四边形各边中点所得的四边形叫做中点四边形，则任意矩形的中点四边形是 A.矩形 7. 式子 B.正方形 226  运算结果是 A. 10 B . 10+2 6 8. 下列各命题的逆命题不成立的是 A．两直线平行，内错角相等 b ，那么 a b C．如果 2 a 2 C .平行四边形 D. 菱形 C.10+4 6 D. 8+2 6 B．若两个数的绝对值相等，则这两个数也相等 D．对顶角相等 9. 如图，在菱形 ABCD中，对角线 AC与 BD相交于点 O，AB=5，AC=6，过点 D 作 DE∥AC交 BC的延长线于点 E，则△BDE的面积为 A. 22 B. 24 10．实数 a在数轴上的位置如图所示，化简 A. 1 B. －1 a C.26 ( 2   C. 2a－3 D. 28 a 2 1)  的结果是 D. 3－2a 11．已知△ABC中，AB＝13，AC＝15，AD⊥BC于 D，且 AD＝12，则 BC的长为 A. 14 B. 4 C.14 或 4 D. 14 或 9 12．如下图是一个按某种规律排列的数阵: 3 2 2 7 1 2 3 2 5 10 6 11 2 3 第 1 行第 2 行第 3 行

13 14 15 4 17 3 2 19 2 5 第 4 行 … … … … … … … … … 根据数阵排列的规律，第 6 行从左向右数第 5 个数是 37 B. 35 C. A. 34 D. 38 二、填空题：（本大题共 6 小题，每小题 3 分，共 18 分）把答案填在答题卡中的横线上． 13. 比较大小： 2 3 14. 如图，在△ABC中，∠ACB=90°．CD为 AB边上的中线，若∠A =55°，则∠BCD的度数为 13 ．．第 14 题图第 15 题图第 17 题图第 18 题图 15. 将一副三角尺按图所示的方式叠放在一起，如果 AF= 2 ，那么 AB= ． 16. 若 a  1   t 1 4  2 1   ， b  t 1 4  2 ，则 ab a b ＝（结果用含 t的式子表示）． 17. 如图，在正方形 ABCD的外侧，作等边三角形 ADE，AC、BE相交于点 F，则∠AFE的度数为 18. 如图，已知正方形 ABCD的边长为 6，点 E在 AB边上且 BE＝2，点 P，Q分别是边 BC，CD的动点（均不度．与顶点重合），则四边形 AEPQ的最小周长是．三、解答题：（本大题共 8 小题，满分共 66 分）解答应写出证明过程或演算步骤（含相应的文字说明），将解答写在答题卡上． 19．(6 分）计算： ( 8  3)  6 4  1 2 ． 20.（6 分）先化简，再求值：    1  x  y 1  x    y  1  xy 2 y ，其中， x 12  ， y 12  ． 21.（6 分）如图，四边形 ABCD中，AB＝DC，AD＝BC，点 E在 AD上，点 F在 BC上，AE＝CF，EF与对角线 BD交于点 O．求证：四边形 BEDF是平行四边形．

22.（8 分）如图所示，在四边形 ABCD 中，∠B= 90°， AB=3， BC=4, CD=12， AD=13，求四边形 ABCD 的面积． 23.（9分）如图，一艘船由A港沿北偏东60°方向航行12 km至B港，然后再沿北偏西30°方向航行12km至C 港．求A、C 两港之间的距离（结果保留根号）． 24.（9 分）如图，在平行四边形 ABCD中，点 E是 CD的中点，点 F是 BC边上的一点，且 EF⊥AE．求证：AE平分∠DAF．李华同学读题后有一个想法，延长 FE，AD交于点 M，要证 AE平分∠DAF，只需证△AMF是等腰三角形即可．请你参考李华的想法，完成此题的证明． 25.（10 分）如图，在矩形 ABCD中，AB＝5，AD＝4，Q 是 AD上一点，将△CDQ沿 CQ折叠，D 点正好与 AB 边上 P（不与 A，B重合）点重合，连接 CP．（1）求 DQ的长；（2）取 CQ的中点 M，连接 MD，MP，DP，求△MDP的面积．

26.（12 分）在 Rt△ABC中，∠B=90°，AC =20，∠A=60°，点 D从点 C出发沿 CA方向以每秒 2 个单位长的速度向点 A匀速运动，同时点 E从点 A出发沿 AB方向以每秒 1 个单位长的速度向点 B匀速运动，当其中一个点到达终点时，另一个点也随之停止运动，设点 D、E运动的时间是 t秒(t>0)，过点 D作 DF ⊥BC于点 F，连接 DE、EF． (1)求证：四边形 AEFD是平行四边形； (2)四边形 AEFD能够成为菱形吗？如果能，求出相应的 t值；如果不能，说明理由； (3)当 t为何值时，△DEF为直角三角形？请说明理由．

八年级数学参考答案及评分标准一、选择题：（每小题 3 分，共 36 分）题号 1 答案 B 2 C 3 D 4 B 5 A 6 D 7 C 8 D 9 B 10 11 12 A C B 二、填空题：（每小题 3 分，共 18 分） 13. ＜ 14. 35° 15. 2 16. －t 17. 60 18. 4 13  4 三、解答题：（8 小题满分 66 分） ....................3 分 .....................5 分 ....................6 分 ..........1 分 = 34 2  ． 12   12      12 12   2 x  xy  xy  y   =2-1=1 ， 2 ， .........2 分  y .........4 分 19. 解：原式   = 48+ 18 4 2 2 222334   = 20. 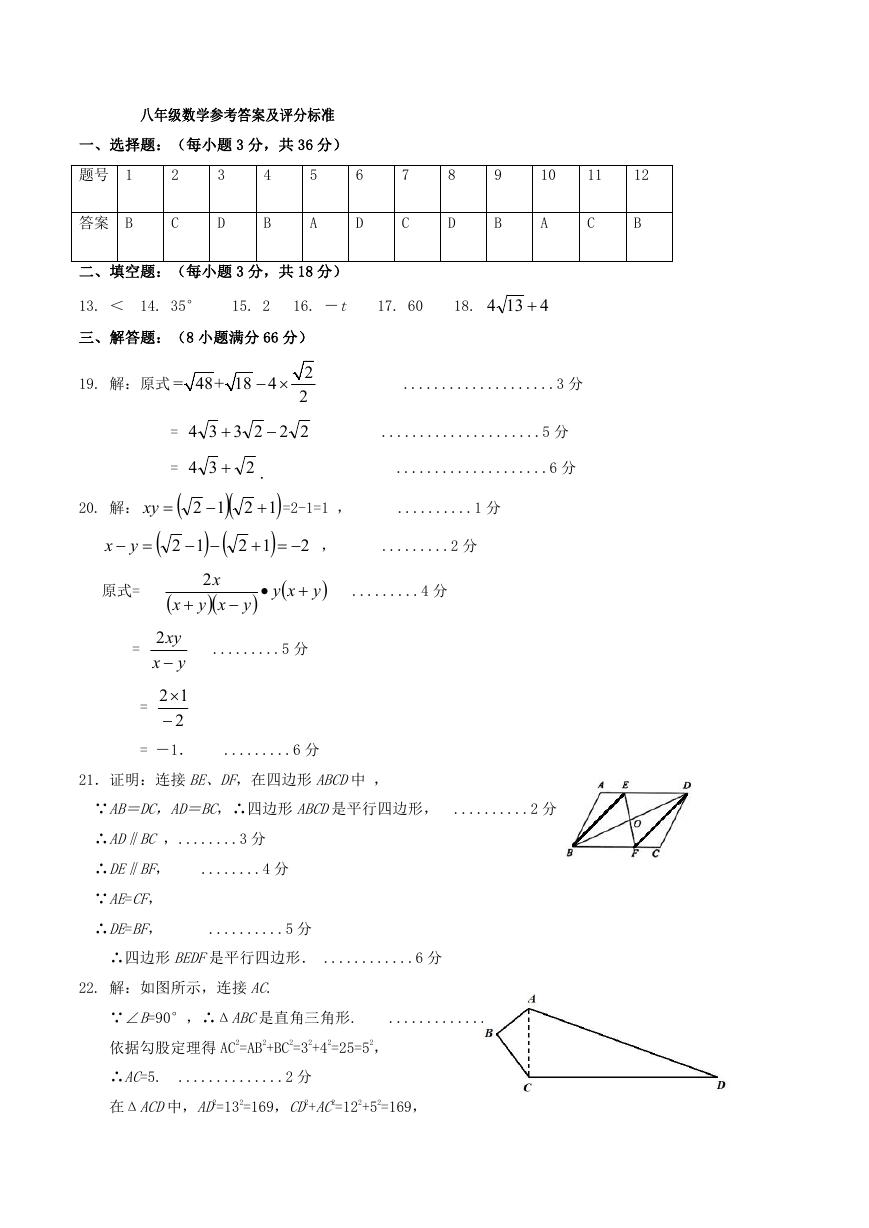解： xy  x  y 原式= =   x 2 xy x y  12  2  = －1． = .........5 分 .........6 分 21．证明：连接 BE、DF，在四边形 ABCD中， ∵AB＝DC，AD＝BC，∴四边形 ABCD是平行四边形， ..........2 分 ∴AD‖BC ，........3 分 ∴DE‖BF， ........4 分 ∵AE=CF， ∴DE=BF， ..........5 分 ∴四边形 BEDF是平行四边形． ............6 分 22. 解：如图所示，连接 AC. ∵∠B=90°，∴ΔABC是直角三角形. ..............1 分依据勾股定理得 AC2=AB2+BC2=32+42=25=52， ∴AC=5. ..............2 分在ΔACD中，AD2=132=169，CD2+AC2=122+52=169，

∴AD2=AC2+CD2. ∴ΔACD是直角三角形，∠ACD=90°. ............. 4 分 ∴S 四边形 ABCD=SΔABC+SΔACD = 1 2 = 1 2 AB•BC+ 1 2 ×4×3+ 1 2 AC•CD ×5×12 .............6 分 =6+30=36. ..............7 分 ∴四边形 ABCD的面积为 36. ................8 分 23. 解：∵∠MAB=60°，∴∠BAN=30° ，........２分 ∵AN‖QB，∴∠QBA=∠BAN=30°， ........４分 ∵∠PBC=30°，∴∠CBQ=60°， ∴∠ABC=∠QBA+∠CBQ=90°，.........６分根据勾股定理， AC  2 AB  BC 2 = 12 +12 2 2  12 2 ，...........8 分 ∴A、C 两港之间的距离是12 2 km．..............9 分 24．证明：延长 AD，FE交于 M．在平行四边形 ABCD中，AD∥BC， ∴∠MDE=∠FCE，∠EMD=∠EFC, ............2 分又 E是 CD的中点，∴DE= CE，............3 分 ∴△EDM≌△ECF，........4 分 ∴EM= EF， ........5 分又 EF⊥AE，∴AF=AM，即△AMF是等腰三角形， .........7 分又 AE⊥FM，∴AE平分∠DAF． ..........9 分 25．解：（1）在矩形 ABCD中，∠A=∠B=90°，AD = BC =4， .......1 分由题意知，PC =DC =5，DQ=PQ，在 Rt△PBC 中，根据勾股定理得 PB= PC  2 BC 2 = 2 4 5  2 =3，........2 分 ∴PA=2 ........3 分设 DQ=PQ=x，在 Rt△PAQ 中，根据勾股定理得， 2 PQ  2 x   4 AQ  x  2  PA 2 2  2 2 ......4 分

解得 5x 2 所以，DQ 的长为 5 2 ； ......5 分（2）如图，∵M 是 QC 的中点， SΔDQC＝     1 2  DQ CD     ＝ 25 8 ， ........6 分 SΔPQC＝，.........7 分 1 ∴SΔDQM＝ 2 SΔPQM ＝ 1 2 1 2 25 8 25 8 ∴ S 四边形 PQDM   2= ∵SΔPQD＝ 1 2 DQ  PA  5 2 ，........8 分 25 4 ， SΔMDP＝ S 四边形 P Q D M S Δ P Q D = 25 4   5 2 15 4 ， ∴△MDP的面积为 15 4 ． .......... 10 分 26. 解：(1)在△ABC中，∠B=90°，∠A=60°，∴∠C=30°， ......1 分 ∵DF⊥BC，∴∠DFC=90° ∵DC=2t，∴DF=t． ......2 分又∵AE=t，∴AE=DF； ......3 分 ∵∠B=∠DFC=90°，∴ AE∥DF ∴四边形 AEFD 是平行四边形 ........4 分（2）能； ........5 分理由如下：由（1）知，四边形 AEFD 为平行四边形．且∠C=30° 又∵AC=20，∴AD=AC-DC=20-2t，........6 分若 AE=AD，则平行四边形 AEFD 为菱形，.......7 分 ∴t=20-2t， ∴ t  20 3 ；.........8 分（3）当 t=5 或 8 时，△DEF 为直角三角形；.........9 分理由如下： ①∠EDF=90°时，四边形 EBFD 为矩形．在 Rt△AED 中，∠ADE=∠C=30°，∴AD=2AE．即 20-2t=2t， ∴t=5； .........10 分

②∠DEF=90°时，∵四边形 AEFD 是平行四边形， ∴EF∥AD，∴∠ADE=∠DEF=90°． ∵在 Rt△ADE 中，∠A=60°，∴∠AED=30°， ∴AD= 1 2 AE，即 20-2t= 1 2 t，∴t=8； ....... 11 分 ③∠EFD=90°时，此种情况不存在；综上所述，当 t=5 或 8 时，△DEF 为直角三角形． .......12 分

资料库

2020-2021学年广西玉林市博白县八年级下学期期中数学试题及答案.doc

相关推荐

初中二年级

热门标签

最新资料