ORB: an efficient alternative to SIFT or SURF
Ethan Rublee
Vincent Rabaud
Kurt Konolige
Gary Bradski
Willow Garage, Menlo Park, California
{erublee}{vrabaud}{konolige}{bradski}@willowgarage.com
Abstract
Feature matching is at the base of many computer vi-
sion problems, such as object recognition or structure from
motion. Current methods rely on costly descriptors for de-
tection and matching. In this paper, we propose a very fast
binary descriptor based on BRIEF, called ORB, which is
rotation invariant and resistant to noise. We demonstrate
through experiments how ORB is at two orders of magni-
tude faster than SIFT, while performing as well in many
situations. The efficiency is tested on several real-world ap-
plications, including object detection and patch-tracking on
a smart phone.
1. Introduction
The SIFT keypoint detector and descriptor [17], al-
though over a decade old, have proven remarkably success-
ful in a number of applications using visual features, in-
cluding object recognition [17], image stitching [28], visual
mapping [25], etc. However, it imposes a large computa-
tional burden, especially for real-time systems such as vi-
sual odometry, or for low-power devices such as cellphones.
This has led to an intensive search for replacements with
lower computation cost; arguably the best of these is SURF
[2]. There has also been research aimed at speeding up the
computation of SIFT, most notably with GPU devices [26].
In this paper, we propose a computationally-efficient re-
placement to SIFT that has similar matching performance,
is less affected by image noise, and is capable of being used
for real-time performance. Our main motivation is to en-
hance many common image-matching applications, e.g., to
enable low-power devices without GPU acceleration to per-
form panorama stitching and patch tracking, and to reduce
the time for feature-based object detection on standard PCs.
Our descriptor performs as well as SIFT on these tasks (and
better than SURF), while being almost two orders of mag-
nitude faster.
Our proposed feature builds on the well-known FAST
keypoint detector [23] and the recently-developed BRIEF
descriptor [6]; for this reason we call it ORB (Oriented
Figure 1. Typical matching result using ORB on real-world im-
ages with viewpoint change. Green lines are valid matches; red
circles indicate unmatched points.
FAST and Rotated BRIEF). Both these techniques are at-
tractive because of their good performance and low cost.
In this paper, we address several limitations of these tech-
niques vis-a-vis SIFT, most notably the lack of rotational
invariance in BRIEF. Our main contributions are:
nent to FAST.
• The addition of a fast and accurate orientation compo-
• The efficient computation of oriented BRIEF features.
• Analysis of variance and correlation of oriented
• A learning method for de-correlating BRIEF features
under rotational invariance, leading to better perfor-
mance in nearest-neighbor applications.
BRIEF features.
To validate ORB, we perform experiments that test the
properties of ORB relative to SIFT and SURF, for both
raw matching ability, and performance in image-matching
applications. We also illustrate the efficiency of ORB
by implementing a patch-tracking application on a smart
phone. An additional benefit of ORB is that it is free from
the licensing restrictions of SIFT and SURF.
2. Related Work
Keypoints FAST and its variants [23, 24] are the method
of choice for finding keypoints in real-time systems that
match visual features, for example, Parallel Tracking and
Mapping [13].
It is efficient and finds reasonable corner
keypoints, although it must be augmented with pyramid
1
�
schemes for scale [14], and in our case, a Harris corner filter
[11] to reject edges and provide a reasonable score.
Many keypoint detectors include an orientation operator
(SIFT and SURF are two prominent examples), but FAST
does not. There are various ways to describe the orientation
of a keypoint; many of these involve histograms of gradient
computations, for example in SIFT [17] and the approxi-
mation by block patterns in SURF [2]. These methods are
either computationally demanding, or in the case of SURF,
yield poor approximations. The reference paper by Rosin
[22] gives an analysis of various ways of measuring orienta-
tion of corners, and we borrow from his centroid technique.
Unlike the orientation operator in SIFT, which can have
multiple value on a single keypoint, the centroid operator
gives a single dominant result.
Descriptors BRIEF [6] is a recent feature descriptor that
uses simple binary tests between pixels in a smoothed image
patch. Its performance is similar to SIFT in many respects,
including robustness to lighting, blur, and perspective dis-
tortion. However, it is very sensitive to in-plane rotation.
BRIEF grew out of research that uses binary tests to
train a set of classification trees [4]. Once trained on a set
of 500 or so typical keypoints, the trees can be used to re-
turn a signature for any arbitrary keypoint [5]. In a similar
manner, we look for the tests least sensitive to orientation.
The classic method for finding uncorrelated tests is Princi-
pal Component Analysis; for example, it has been shown
that PCA for SIFT can help remove a large amount of re-
dundant information [12]. However, the space of possible
binary tests is too big to perform PCA and an exhaustive
search is used instead.
Visual vocabulary methods [21, 27] use offline clustering
to find exemplars that are uncorrelated and can be used in
matching. These techniques might also be useful in finding
uncorrelated binary tests.
The closest system to ORB is [3], which proposes a
multi-scale Harris keypoint and oriented patch descriptor.
This descriptor is used for image stitching, and shows good
rotational and scale invariance. It is not as efficient to com-
pute as our method, however.
3. oFAST: FAST Keypoint Orientation
FAST features are widely used because of their compu-
tational properties. However, FAST features do not have an
orientation component. In this section we add an efficiently-
computed orientation.
3.1. FAST Detector
We start by detecting FAST points in the image. FAST
takes one parameter, the intensity threshold between the
center pixel and those in a circular ring about the center.
We use FAST-9 (circular radius of 9), which has good per-
formance.
FAST does not produce a measure of cornerness, and we
have found that it has large responses along edges. We em-
ploy a Harris corner measure [11] to order the FAST key-
points. For a target number N of keypoints, we first set the
threshold low enough to get more than N keypoints, then
order them according to the Harris measure, and pick the
top N points.
FAST does not produce multi-scale features. We employ
a scale pyramid of the image, and produce FAST features
(filtered by Harris) at each level in the pyramid.
3.2. Orientation by Intensity Centroid
Our approach uses a simple but effective measure of cor-
ner orientation, the intensity centroid [22]. The intensity
centroid assumes that a corner’s intensity is offset from its
center, and this vector may be used to impute an orientation.
Rosin defines the moments of a patch as:
mpq = Xx,y
xpyqI(x, y),
and with these moments we may find the centroid:
C = m10
m00
,
m01
m00
(1)
(2)
We can construct a vector from the corner’s center, O, to the
centroid, ~OC. The orientation of the patch then simply is:
θ = atan2(m01, m10),
(3)
where atan2 is the quadrant-aware version of arctan. Rosin
mentions taking into account whether the corner is dark or
light; however, for our purposes we may ignore this as the
angle measures are consistent regardless of the corner type.
To improve the rotation invariance of this measure we
make sure that moments are computed with x and y re-
maining within a circular region of radius r. We empirically
choose r to be the patch size, so that that x and y run from
[−r, r]. As |C| approaches 0, the measure becomes unsta-
ble; with FAST corners, we have found that this is rarely the
case.
We compared the centroid method with two gradient-
based measures, BIN and MAX. In both cases, X and
Y gradients are calculated on a smoothed image. MAX
chooses the largest gradient in the keypoint patch; BIN
forms a histogram of gradient directions at 10 degree inter-
vals, and picks the maximum bin. BIN is similar to the SIFT
algorithm, although it picks only a single orientation. The
variance of the orientation in a simulated dataset (in-plane
rotation plus added noise) is shown in Figure 2. Neither of
the gradient measures performs very well, while the cen-
troid gives a uniformly good orientation, even under large
image noise.
�
Standard Deviation in Angle Error
Histogram of Descriptor Bit Mean Values
)
s
e
e
r
g
e
d
(
n
o
i
t
i
a
v
e
D
d
r
a
d
n
a
S
t
40
35
30
25
20
15
10
5
0
IC
MAX
BIN
5
10
15
20
25
Image Intensity Noise (gaussian noise for an 8 bit image)
Figure 2. Rotation measure. The intensity centroid (IC) per-
forms best on recovering the orientation of artificially rotated noisy
patches, compared to a histogram (BIN) and MAX method.
4. rBRIEF: Rotation-Aware Brief
In this section, we first introduce a steered BRIEF de-
scriptor, show how to compute it efficiently and demon-
strate why it actually performs poorly with rotation. We
then introduce a learning step to find less correlated binary
tests leading to the better descriptor rBRIEF, for which we
offer comparisons to SIFT and SURF.
4.1. Efficient Rotation of the BRIEF Operator
Brief overview of BRIEF
The BRIEF descriptor [6] is a bit string description of an
image patch constructed from a set of binary intensity tests.
Consider a smoothed image patch, p. A binary test τ is
defined by:
BRIEF
rBRIEF
steered BRIEF
s
t
i
B
f
o
r
e
b
m
u
N
140
120
100
80
60
40
20
0
0
0.0
5
0.1
0.1
5
0.2
0.2
5
0.3
0.3
5
0.4
0.4
5
0.5
Bit Response Mean
Figure 3. Distribution of means for feature vectors: BRIEF, steered
BRIEF (Section 4.1), and rBRIEF (Section 4.3). The X axis is the
distance to a mean of 0.5
but this solution is obviously expensive. A more efficient
method is to steer BRIEF according to the orientation of
keypoints. For any feature set of n binary tests at location
(xi, yi), define the 2 × n matrix
S = x1, . . . , xn
y1, . . . , yn
Using the patch orientation θ and the corresponding rotation
matrix Rθ, we construct a “steered” version Sθ of S:
Sθ = RθS,
(4)
Now the steered BRIEF operator becomes
τ (p; x, y) := 1 : p(x) < p(y)
0 : p(x) ≥ p(y)
,
where p(x) is the intensity of p at a point x. The feature is
defined as a vector of n binary tests:
fn(p) := X1≤i≤n
2i−1τ (p; xi, yi)
(5)
Many different types of distributions of tests were consid-
ered in [6]; here we use one of the best performers, a Gaus-
sian distribution around the center of the patch. We also
choose a vector length n = 256.
It is important to smooth the image before performing
the tests. In our implementation, smoothing is achieved us-
ing an integral image, where each test point is a 5 × 5 sub-
window of a 31 × 31 pixel patch. These were chosen from
our own experiments and the results in [6].
Steered BRIEF
We would like to allow BRIEF to be invariant to in-plane
rotation. Matching performance of BRIEF falls off sharply
for in-plane rotation of more than a few degrees (see Figure
7). Calonder [6] suggests computing a BRIEF descriptor
for a set of rotations and perspective warps of each patch,
gn(p, θ) := fn(p)|(xi, yi) ∈ Sθ
(6)
We discretize the angle to increments of 2π/30 (12 de-
grees), and construct a lookup table of precomputed BRIEF
patterns. As long at the keypoint orientation θ is consistent
across views, the correct set of points Sθ will be used to
compute its descriptor.
4.2. Variance and Correlation
One of the pleasing properties of BRIEF is that each bit
feature has a large variance and a mean near 0.5. Figure 3
shows the spread of means for a typical Gaussian BRIEF
pattern of 256 bits over 100k sample keypoints. A mean
of 0.5 gives the maximum sample variance 0.25 for a bit
feature. On the other hand, once BRIEF is oriented along
the keypoint direction to give steered BRIEF, the means are
shifted to a more distributed pattern (again, Figure 3). One
way to understand this is that the oriented corner keypoints
present a more uniform appearance to binary tests.
High variance makes a feature more discriminative, since
it responds differentially to inputs. Another desirable prop-
erty is to have the tests uncorrelated, since then each test
will contribute to the result. To analyze the correlation and
�
l
e
u
a
v
n
e
g
E
i
8
6
4
2
0
0
BRIEF
Steered BRIEF
rBRIEF
5
10
15
20
25
30
35
40
Component
Figure 4. Distribution of eigenvalues in the PCA decomposition
over 100k keypoints of three feature vectors: BRIEF, steered
BRIEF (Section 4.1), and rBRIEF (Section 4.3).
y
c
n
e
u
q
e
r
F
e
v
i
t
l
a
e
R
0.04
0.035
0.03
0.025
0.02
0.015
0.01
0.005
0
0
Distance Distribution
rBRIEF
steered BRIEF
BRIEF
64
128
192
256
Descriptor Distance
Figure 5. The dotted lines show the distances of a keypoint to out-
liers, while the solid lines denote the distances only between inlier
matches for three feature vectors: BRIEF, steered BRIEF (Section
4.1), and rBRIEF (Section 4.3).
variance of tests in the BRIEF vector, we looked at the re-
sponse to 100k keypoints for BRIEF and steered BRIEF.
The results are shown in Figure 4. Using PCA on the data,
we plot the highest 40 eigenvalues (after which the two de-
scriptors converge). Both BRIEF and steered BRIEF ex-
hibit high initial eigenvalues, indicating correlation among
the binary tests – essentially all the information is contained
in the first 10 or 15 components. Steered BRIEF has signif-
icantly lower variance, however, since the eigenvalues are
lower, and thus is not as discriminative. Apparently BRIEF
depends on random orientation of keypoints for good per-
formance. Another view of the effect of steered BRIEF is
shown in the distance distributions between inliers and out-
liers (Figure 5). Notice that for steered BRIEF, the mean for
outliers is pushed left, and there is more of an overlap with
the inliers.
4.3. Learning Good Binary Features
To recover from the loss of variance in steered BRIEF,
and to reduce correlation among the binary tests, we de-
velop a learning method for choosing a good subset of bi-
nary tests. One possible strategy is to use PCA or some
other dimensionality-reduction method, and starting from a
large set of binary tests, identify 256 new features that have
high variance and are uncorrelated over a large training set.
However, since the new features are composed from a larger
number of binary tests, they would be less efficient to com-
pute than steered BRIEF. Instead, we search among all pos-
sible binary tests to find ones that both have high variance
(and means close to 0.5), as well as being uncorrelated.
The method is as follows. We first set up a training set of
some 300k keypoints, drawn from images in the PASCAL
2006 set [8]. We also enumerate all possible binary tests
drawn from a 31×31 pixel patch. Each test is a pair of 5×5
sub-windows of the patch. If we note the width of our patch
as wp = 31 and the width of the test sub-window as wt = 5,
then we have N = (wp − wt)2 possible sub-windows. We
would like to select pairs of two from these, so we haveN
2
binary tests. We eliminate tests that overlap, so we end up
with M = 205590 possible tests. The algorithm is:
1. Run each test against all training patches.
2. Order the tests by their distance from a mean of 0.5,
forming the vector T.
3. Greedy search:
(a) Put the first test into the result vector R and re-
move it from T.
(b) Take the next test from T, and compare it against
all tests in R. If its absolute correlation is greater
than a threshold, discard it; else add it to R.
(c) Repeat the previous step until there are 256 tests
in R. If there are fewer than 256, raise the thresh-
old and try again.
This algorithm is a greedy search for a set of uncorrelated
tests with means near 0.5. The result is called rBRIEF.
rBRIEF has significant improvement in the variance and
correlation over steered BRIEF (see Figure 4). The eigen-
values of PCA are higher, and they fall off much less
quickly. It is interesting to see the high-variance binary tests
produced by the algorithm (Figure 6). There is a very pro-
nounced vertical trend in the unlearned tests (left image),
which are highly correlated; the learned tests show better
diversity and lower correlation.
4.4. Evaluation
We evaluate the combination of oFAST and rBRIEF,
which we call ORB, using two datasets: images with syn-
thetic in-plane rotation and added Gaussian noise, and a
real-world dataset of textured planar images captured from
different viewpoints. For each reference image, we compute
the oFAST keypoints and rBRIEF features, targeting 500
keypoints per image. For each test image (synthetic rotation
or real-world viewpoint change), we do the same, then per-
form brute-force matching to find the best correspondence.
�
s
r
e
i
l
n
I
f
o
e
g
a
t
n
e
c
r
e
P
100
95
90
85
80
75
70
65
60
55
50
45
40
35
Comparison of SIFT and rBRIEF considering Gaussian Intensity Noise
rBRIEF
SIFT
90
180
270
360
Angle of Rotation (Degrees)
Figure 8. Matching behavior under noise for SIFT and rBRIEF.
The noise levels are 0, 5, 10, 15, 20, and 25. SIFT performance
degrades rapidly, while rBRIEF is relatively unaffected.
Figure 9. Real world data of a table full of magazines and an out-
door scene. The images in the first column are matched to those in
the second. The last column is the resulting warp of the first onto
the second.
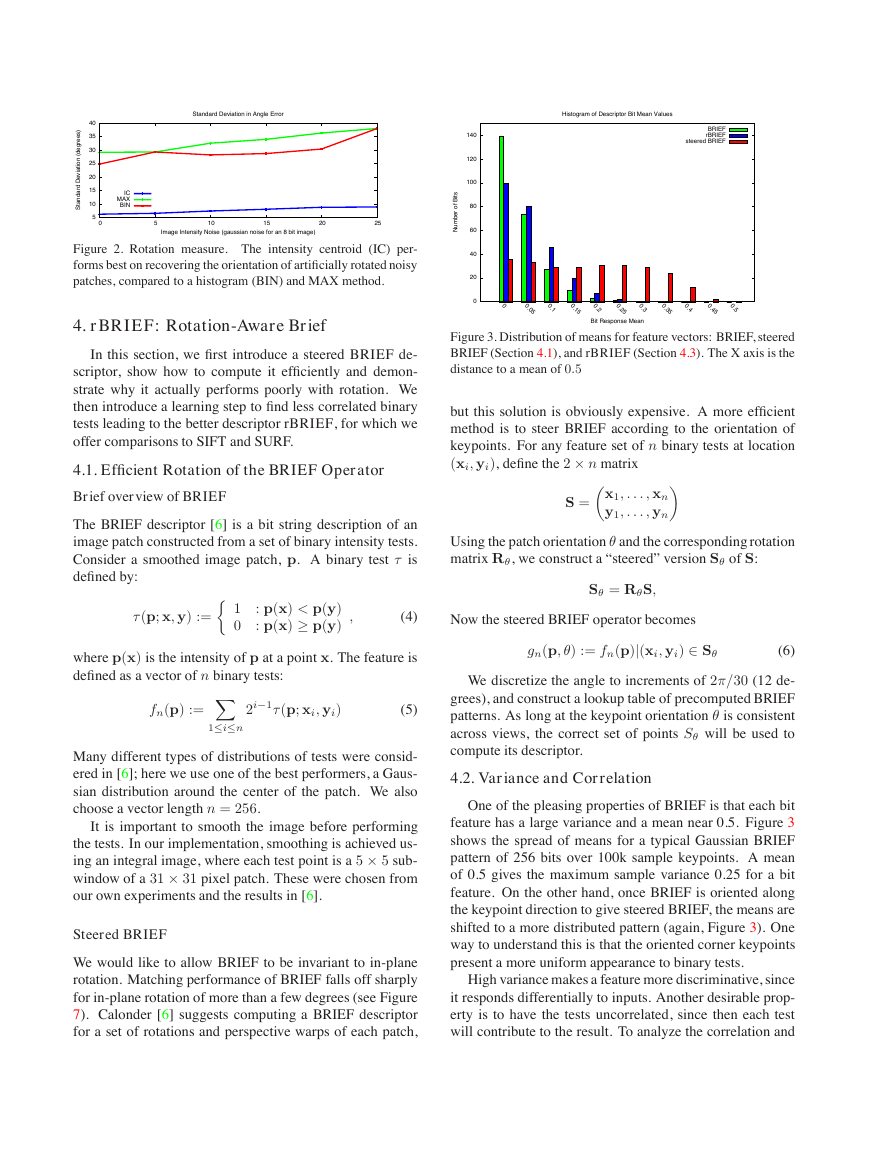
we measure the performance of ORB relative to SIFT and
SURF. The test is performed in the following manner:
1. Pick a reference view V0.
2. For all Vi, find a homographic warp Hi0 that maps
Vi → V0.
matches from SIFT, SURF, and ORB.
3. Now, use the Hi0 as ground truth for descriptor
inlier % N points
Magazines
ORB 36.180
SURF
38.305
SIFT 34.010
548.50
513.55
584.15
Boat
ORB 45.8
SURF
28.6
SIFT 30.2
789
795
714
ORB outperforms SIFT and SURF on the outdoor dataset.
It is about the same on the indoor set; [6] noted that blob-
detection keypoints like SIFT tend to be better on graffiti-
type images.
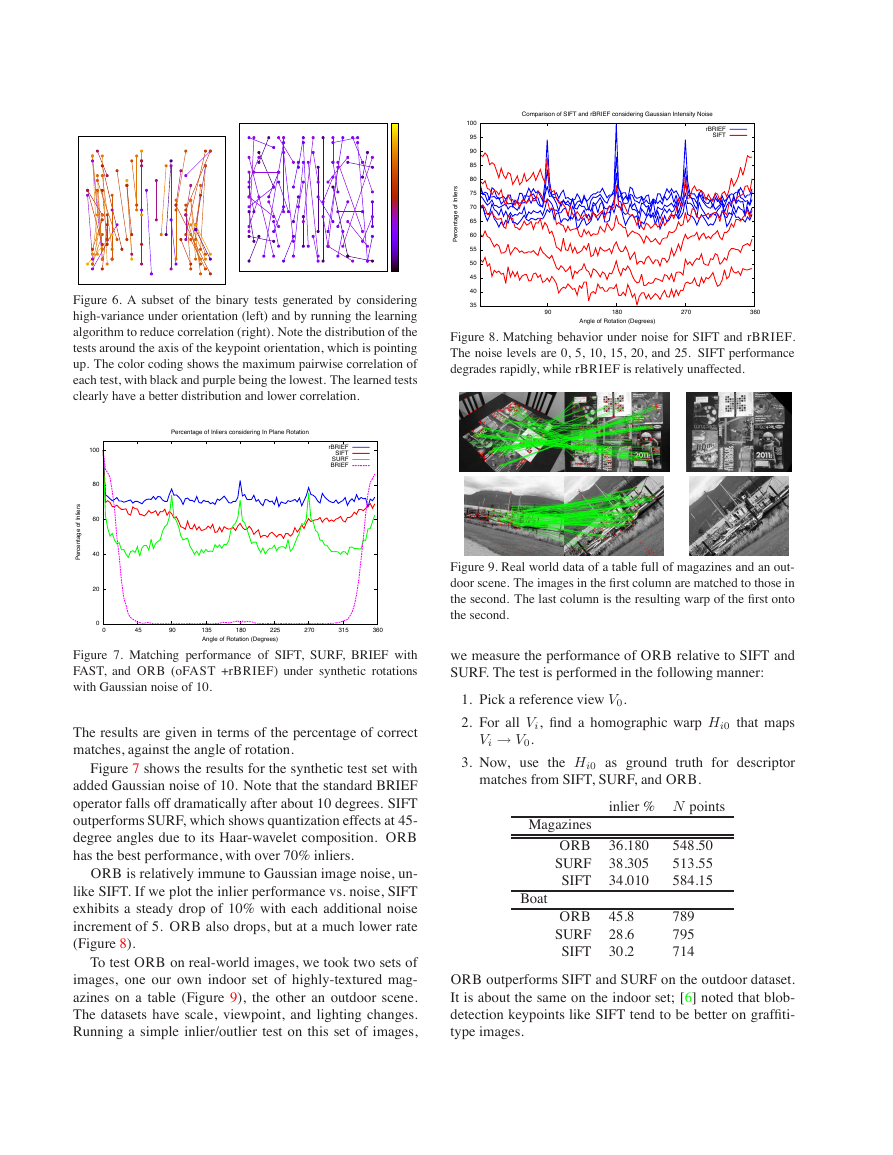
Figure 6. A subset of the binary tests generated by considering
high-variance under orientation (left) and by running the learning
algorithm to reduce correlation (right). Note the distribution of the
tests around the axis of the keypoint orientation, which is pointing
up. The color coding shows the maximum pairwise correlation of
each test, with black and purple being the lowest. The learned tests
clearly have a better distribution and lower correlation.
Percentage of Inliers considering In Plane Rotation
rBRIEF
SIFT
SURF
BRIEF
100
80
60
40
20
s
r
e
i
l
n
I
f
o
e
g
a
t
n
e
c
r
e
P
0
0
45
90
135
225
Angle of Rotation (Degrees)
180
270
315
360
Figure 7. Matching performance of SIFT, SURF, BRIEF with
FAST, and ORB (oFAST +rBRIEF) under synthetic rotations
with Gaussian noise of 10.
The results are given in terms of the percentage of correct
matches, against the angle of rotation.
Figure 7 shows the results for the synthetic test set with
added Gaussian noise of 10. Note that the standard BRIEF
operator falls off dramatically after about 10 degrees. SIFT
outperforms SURF, which shows quantization effects at 45-
degree angles due to its Haar-wavelet composition. ORB
has the best performance, with over 70% inliers.
ORB is relatively immune to Gaussian image noise, un-
like SIFT. If we plot the inlier performance vs. noise, SIFT
exhibits a steady drop of 10% with each additional noise
increment of 5. ORB also drops, but at a much lower rate
(Figure 8).
To test ORB on real-world images, we took two sets of
images, one our own indoor set of highly-textured mag-
azines on a table (Figure 9), the other an outdoor scene.
The datasets have scale, viewpoint, and lighting changes.
Running a simple inlier/outlier test on this set of images,
�
106
105
104
103
102
101
100
106
105
104
103
102
101
100
s
t
e
k
c
u
b
f
o
r
e
b
m
u
N
Caltech 101 - BRIEF
Caltech 101 - steered BRIEF
Caltech 101 - rBRIEF
0 20 40 60 80 100 120 140 160 180 200 220 240 260 280 300 320 340
Pascal 2009 - BRIEF
Pascal 2009 - steered BRIEF
Pascal 2009 - rBRIEF
103
102
101
)
s
m
(
e
r
u
t
a
e
f
r
e
p
e
m
i
t
y
r
e
u
Q
0
400 800 1200 1600 2000 2400 2800 3200 3600 4000 4400 4800
Bucket size
100
20
40
80
Success percentage
60
rBRIEF
steered BRIEF
SIFT
100
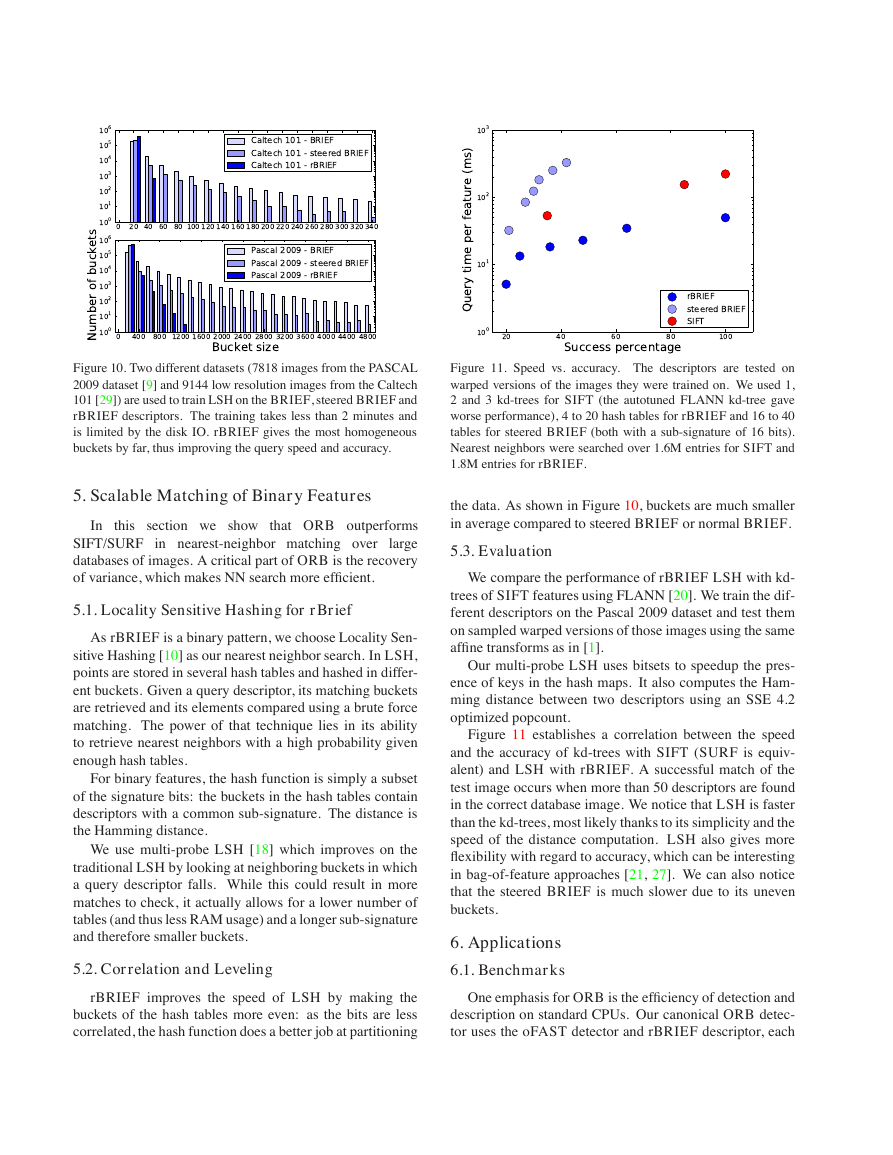
Figure 10. Two different datasets (7818 images from the PASCAL
2009 dataset [9] and 9144 low resolution images from the Caltech
101 [29]) are used to train LSH on the BRIEF, steered BRIEF and
rBRIEF descriptors. The training takes less than 2 minutes and
is limited by the disk IO. rBRIEF gives the most homogeneous
buckets by far, thus improving the query speed and accuracy.
5. Scalable Matching of Binary Features
In this
section we show that ORB outperforms
SIFT/SURF in nearest-neighbor matching over
large
databases of images. A critical part of ORB is the recovery
of variance, which makes NN search more efficient.
5.1. Locality Sensitive Hashing for rBrief
As rBRIEF is a binary pattern, we choose Locality Sen-
sitive Hashing [10] as our nearest neighbor search. In LSH,
points are stored in several hash tables and hashed in differ-
ent buckets. Given a query descriptor, its matching buckets
are retrieved and its elements compared using a brute force
matching. The power of that technique lies in its ability
to retrieve nearest neighbors with a high probability given
enough hash tables.
For binary features, the hash function is simply a subset
of the signature bits: the buckets in the hash tables contain
descriptors with a common sub-signature. The distance is
the Hamming distance.
We use multi-probe LSH [18] which improves on the
traditional LSH by looking at neighboring buckets in which
a query descriptor falls. While this could result in more
matches to check, it actually allows for a lower number of
tables (and thus less RAM usage) and a longer sub-signature
and therefore smaller buckets.
5.2. Correlation and Leveling
Figure 11. Speed vs. accuracy. The descriptors are tested on
warped versions of the images they were trained on. We used 1,
2 and 3 kd-trees for SIFT (the autotuned FLANN kd-tree gave
worse performance), 4 to 20 hash tables for rBRIEF and 16 to 40
tables for steered BRIEF (both with a sub-signature of 16 bits).
Nearest neighbors were searched over 1.6M entries for SIFT and
1.8M entries for rBRIEF.
the data. As shown in Figure 10, buckets are much smaller
in average compared to steered BRIEF or normal BRIEF.
5.3. Evaluation
We compare the performance of rBRIEF LSH with kd-
trees of SIFT features using FLANN [20]. We train the dif-
ferent descriptors on the Pascal 2009 dataset and test them
on sampled warped versions of those images using the same
affine transforms as in [1].
Our multi-probe LSH uses bitsets to speedup the pres-
ence of keys in the hash maps. It also computes the Ham-
ming distance between two descriptors using an SSE 4.2
optimized popcount.
Figure 11 establishes a correlation between the speed
and the accuracy of kd-trees with SIFT (SURF is equiv-
alent) and LSH with rBRIEF. A successful match of the
test image occurs when more than 50 descriptors are found
in the correct database image. We notice that LSH is faster
than the kd-trees, most likely thanks to its simplicity and the
speed of the distance computation. LSH also gives more
flexibility with regard to accuracy, which can be interesting
in bag-of-feature approaches [21, 27]. We can also notice
that the steered BRIEF is much slower due to its uneven
buckets.
6. Applications
6.1. Benchmarks
rBRIEF improves the speed of LSH by making the
buckets of the hash tables more even: as the bits are less
correlated, the hash function does a better job at partitioning
One emphasis for ORB is the efficiency of detection and
description on standard CPUs. Our canonical ORB detec-
tor uses the oFAST detector and rBRIEF descriptor, each
�
computed separately on five scales of the image, with a scal-
ing factor of √2. We used an area-based interpolation for
efficient decimation.
The ORB system breaks down into the following times
per typical frame of size 640x480. The code was executed
in a single thread running on an Intel i7 2.8 GHz processor:
ORB:
Time (ms)
Pyramid
oFAST rBRIEF
4.43
8.68
2.12
When computing ORB on a set of 2686 images at 5
scales, it was able to detect and compute over 2 × 106 fea-
tures in 42 seconds. Comparing to SIFT and SURF on the
same data, for the same number of features (roughly 1000),
and the same number of scales, we get the following times:
Time per frame (ms)
Detector ORB SURF
217.3
15.3
SIFT
5228.7
These times were averaged over 24 640x480 images from
the Pascal dataset [9]. ORB is an order of magnitude faster
than SURF, and over two orders faster than SIFT.
6.2. Textured object detection
We apply rBRIEF to object recognition by implement-
ing a conventional object recognition pipeline similar to
[19]: we first detect oFAST features and rBRIEF de-
scriptors, match them to our database, and then perform
PROSAC [7] and EPnP [16] to have a pose estimate.
Our database contains 49 household objects, each taken
under 24 views with a 2D camera and a Kinect device from
Microsoft. The testing data consists of 2D images of sub-
sets of those same objects under different view points and
occlusions. To have a match, we require that descriptors are
matched but also that a pose can be computed. In the end,
our pipeline retrieves 61% of the objects as shown in Figure
12.
The algorithm handles a database of 1.2M descriptors
in 200MB and has timings comparable to what we showed
earlier (14 ms for detection and 17ms for LSH matching in
average). The pipeline could be sped up considerably by not
matching all the query descriptors to the training data but
our goal was only to show the feasibility of object detection
with ORB.
6.3. Embedded real-time feature tracking
Tracking on the phone involves matching the live frames
to a previously captured keyframe. Descriptors are stored
with the keyframe, which is assumed to contain a planar
surface that is well textured. We run ORB on each incom-
ing frame, and proced with a brute force descriptor match-
ing against the keyframe. The putative matches from the
descriptor distance are used in a PROSAC best fit homog-
raphy H.
Figure 12. Two images of our textured obejct recognition with
pose estimation. The blue features are the training features super-
imposed on the query image to indicate that the pose of the object
was found properly. Axes are also displayed for each object as
well as a pink label. Top image misses two objects; all are found
in the bottom one.
While there are real-time feature trackers that can run on
a cellphone [15], they usually operate on very small images
(e.g., 120x160) and with very few features. Systems com-
parable to ours [30] typically take over 1 second per image.
We were able to run ORB with 640 × 480 resolution at 7
Hz on a cellphone with a 1GHz ARM chip and 512 MB of
RAM. The OpenCV port for Android was used for the im-
plementation. These are benchmarks for about 400 points
per image:
Time (ms)
ORB Matching H Fit
66.6
20.9
72.8
7. Conclusion
In this paper, we have defined a new oriented descrip-
tor, ORB, and demonstrated its performance and efficiency
relative to other popular features. The investigation of vari-
ance under orientation was critical in constructing ORB
and de-correlating its components, in order to get good per-
formance in nearest-neighbor applications. We have also
contributed a BSD licensed implementation of ORB to the
community, via OpenCV 2.3.
One of the issues that we have not adequately addressed
�
here is scale invariance. Although we use a pyramid scheme
for scale, we have not explored per keypoint scale from
depth cues, tuning the number of octaves, etc.. Future work
also includes GPU/SSE optimization, which could improve
LSH by another order of magnitude.
References
[1] M. Aly, P. Welinder, M. Munich, and P. Perona. Scaling
object recognition: Benchmark of current state of the art
techniques. In First IEEE Workshop on Emergent Issues in
Large Amounts of Visual Data (WS-LAVD), IEEE Interna-
tional Conference on Computer Vision (ICCV), September
2009. 6
[2] H. Bay, T. Tuytelaars, and L. Van Gool. Surf: Speeded up ro-
bust features. In European Conference on Computer Vision,
May 2006. 1, 2
[3] M. Brown, S. Winder, and R. Szeliski. Multi-image match-
ing using multi-scale oriented patches. In Computer Vision
and Pattern Recognition, pages 510–517, 2005. 2
[4] M. Calonder, V. Lepetit, and P. Fua. Keypoint signatures for
In European Conference on
fast learning and recognition.
Computer Vision, 2008. 2
[5] M. Calonder, V. Lepetit, K. Konolige, P. Mihelich, and
P. Fua. High-speed keypoint description and matching us-
ing dense signatures. In Under review, 2009. 2
[6] M. Calonder, V. Lepetit, C. Strecha, and P. Fua. Brief: Bi-
nary robust independent elementary features. In In European
Conference on Computer Vision, 2010. 1, 2, 3, 5
[7] O. Chum and J. Matas. Matching with PROSAC - pro-
gressive sample consensus.
In C. Schmid, S. Soatto, and
C. Tomasi, editors, Proc. of Conference on Computer Vision
and Pattern Recognition (CVPR), volume 1, pages 220–226,
Los Alamitos, USA, June 2005. IEEE Computer Society. 7
PASCAL Visual Ob-
(VOC2006) Results.
ject Classes Challenge
http://pascallin.ecs.soton.ac.uk/challenges/VOC/databases.html.
4
2006
[8] M.
Everingham.
The
[9] M. Everingham, L. Van Gool, C. K. I. Williams, J. Winn,
and A. Zisserman. The PASCAL Visual Object Classes
Challenge 2009 (VOC2009) Results.
http://www.pascal-
network.org/challenges/VOC/voc2009/workshop/index.html.
6, 7
[10] A. Gionis, P. Indyk, and R. Motwani. Similarity search in
high dimensions via hashing. In M. P. Atkinson, M. E. Or-
lowska, P. Valduriez, S. B. Zdonik, and M. L. Brodie, editors,
VLDB’99, Proceedings of 25th International Conference on
Very Large Data Bases, September 7-10, 1999, Edinburgh,
Scotland, UK, pages 518–529. Morgan Kaufmann, 1999. 6
[11] C. Harris and M. Stephens. A combined corner and edge
detector. In Alvey Vision Conference, pages 147–151, 1988.
2
[12] Y. Ke and R. Sukthankar. Pca-sift: A more distinctive rep-
resentation for local image descriptors. In Computer Vision
and Pattern Recognition, pages 506–513, 2004. 2
[13] G. Klein and D. Murray. Parallel tracking and mapping for
small AR workspaces. In Proc. Sixth IEEE and ACM Inter-
national Symposium on Mixed and Augmented Reality (IS-
MAR’07), Nara, Japan, November 2007. 1
[14] G. Klein and D. Murray. Improving the agility of keyframe-
based SLAM. In European Conference on Computer Vision,
2008. 2
[15] G. Klein and D. Murray. Parallel tracking and mapping on a
camera phone. In Proc. Eigth IEEE and ACM International
Symposium on Mixed and Augmented Reality (ISMAR’09),
Orlando, October 2009. 7
[16] V. Lepetit, F. Moreno-Noguer, and P. Fua. EPnP: An accurate
Int. J. Comput. Vision,
O(n) solution to the pnp problem.
81:155–166, February 2009. 7
[17] D. G. Lowe. Distinctive image features from scale-invariant
International Journal of Computer Vision,
keypoints.
60(2):91–110, 2004. 1, 2
[18] Q. Lv, W. Josephson, Z. Wang, M. Charikar, and K. Li.
Multi-probe LSH: efficient indexing for high-dimensional
similarity search. In Proceedings of the 33rd international
conference on Very large data bases, VLDB ’07, pages 950–
961. VLDB Endowment, 2007. 6
[19] M. Martinez, A. Collet, and S. S. Srinivasa. MOPED:
A Scalable and low Latency Object Recognition and Pose
Estimation System.
In IEEE International Conference on
Robotics and Automation. IEEE, 2010. 7
[20] M. Muja and D. G. Lowe. Fast approximate nearest neigh-
bors with automatic algorithm configuration. VISAPP, 2009.
6
[21] D. Nist´er and H. Stew´enius. Scalable recognition with a vo-
cabulary tree. In CVPR, 2006. 2, 6
[22] P. L. Rosin. Measuring corner properties. Computer Vision
and Image Understanding, 73(2):291 – 307, 1999. 2
[23] E. Rosten and T. Drummond. Machine learning for high-
In European Conference on Com-
speed corner detection.
puter Vision, volume 1, 2006. 1
[24] E. Rosten, R. Porter, and T. Drummond. Faster and bet-
ter: A machine learning approach to corner detection. IEEE
Trans. Pattern Analysis and Machine Intelligence, 32:105–
119, 2010. 1
[25] S. Se, D. Lowe, and J. Little. Mobile robot localization and
mapping with uncertainty using scale-invariant visual land-
marks. International Journal of Robotic Research, 21:735–
758, August 2002. 1
[26] S. N. Sinha, J. michael Frahm, M. Pollefeys, and Y. Genc.
Gpu-based video feature tracking and matching. Technical
report, In Workshop on Edge Computing Using New Com-
modity Architectures, 2006. 1
[27] J. Sivic and A. Zisserman. Video google: A text retrieval
approach to object matching in videos. International Con-
ference on Computer Vision, page 1470, 2003. 2, 6
[28] N. Snavely, S. M. Seitz, and R. Szeliski. Skeletal sets for
In Proc. Computer Vision
efficient structure from motion.
and Pattern Recognition, 2008. 1
[29] G. Wang, Y. Zhang, and L. Fei-Fei. Using dependent regions
for object categorization in a generative framework, 2006. 6
[30] A. Weimert, X. Tan, and X. Yang. Natural feature detection
on mobile phones with 3D FAST. Int. J. of Virtual Reality,
9:29–34, 2010. 7
�













 2023年江西萍乡中考道德与法治真题及答案.doc
2023年江西萍乡中考道德与法治真题及答案.doc 2012年重庆南川中考生物真题及答案.doc
2012年重庆南川中考生物真题及答案.doc 2013年江西师范大学地理学综合及文艺理论基础考研真题.doc
2013年江西师范大学地理学综合及文艺理论基础考研真题.doc 2020年四川甘孜小升初语文真题及答案I卷.doc
2020年四川甘孜小升初语文真题及答案I卷.doc 2020年注册岩土工程师专业基础考试真题及答案.doc
2020年注册岩土工程师专业基础考试真题及答案.doc 2023-2024学年福建省厦门市九年级上学期数学月考试题及答案.doc
2023-2024学年福建省厦门市九年级上学期数学月考试题及答案.doc 2021-2022学年辽宁省沈阳市大东区九年级上学期语文期末试题及答案.doc
2021-2022学年辽宁省沈阳市大东区九年级上学期语文期末试题及答案.doc 2022-2023学年北京东城区初三第一学期物理期末试卷及答案.doc
2022-2023学年北京东城区初三第一学期物理期末试卷及答案.doc 2018上半年江西教师资格初中地理学科知识与教学能力真题及答案.doc
2018上半年江西教师资格初中地理学科知识与教学能力真题及答案.doc 2012年河北国家公务员申论考试真题及答案-省级.doc
2012年河北国家公务员申论考试真题及答案-省级.doc 2020-2021学年江苏省扬州市江都区邵樊片九年级上学期数学第一次质量检测试题及答案.doc
2020-2021学年江苏省扬州市江都区邵樊片九年级上学期数学第一次质量检测试题及答案.doc 2022下半年黑龙江教师资格证中学综合素质真题及答案.doc
2022下半年黑龙江教师资格证中学综合素质真题及答案.doc