2016年云南昆明理工大学运筹学考研真题A卷.doc

发布时间：2022-09-16 发布人：admin 分类：说明书资料大小：0.05M 资料格式：doc 举报版权申诉

第1页 / 共3页

第2页 / 共3页

第3页 / 共3页

文本预览

2016 年云南昆明理工大学运筹学考研真题 A 卷一、将正确的答案填在空格处。(每空 1 分，共 10 分) 1、若要求目标函数实现最小化，即 min z =CX，则只需将目标函数最小化变换求目标函数最大化，即令 z′= −z，于是得到目标函数。 2、线性规划约束方程组具有的基解的数目最多是个，一般基可行解的数目要小于基解的数目。 3、单纯形表中基变量的检验数σ=0；非基变量 xj 的检验数σ= 。 4、若原问题有最优解，那么对偶问题也有最优解；两目标函数值的关系为。 5、运输问题中用最小元素法确定初始基本可行解的基本思想是。 6、在目标规划中，引入正偏差变量 d＋表示决策值的部分。 7、在目标规划中，若要求恰好达到目标值，则应要求正、负偏差变量均尽可能地小，这时，目标函数的形式为。 8、在 Dijkstra 方法中，表示从 vs 到该点的最短路的权，称为 9、在运输网络中，每个弧上的流量不能超过该弧的。。 10 、网络计划的工期优化是指尽量缩短工程项目的完工工期。主要可采取的措施：。二、解释下列名词。(每题 2 分，共 8 分) 1、最优解 2、表上作业法 3、状态转移方程 4、树图三、回答下列问题。(每题 4 分，共 12 分) 1、阐述单纯形法解求线性规划问题中的最优解的判别定理。 2、用表上作业法求解运输问题时，怎样画闭回路。写出动态规划基本方程的逆序解法的一般表达形式。四、用大 M 法求解下列线性规划问题，并指出问题的解属于哪一类。(30 分) x  1 2  x x 2 x  3 4  3 20  16  max 2 z  2 4 x x   1  2 4 x x   1  4 8 x x   1  , , xxx  1 3 2 2 2 x 3 2  2 0 

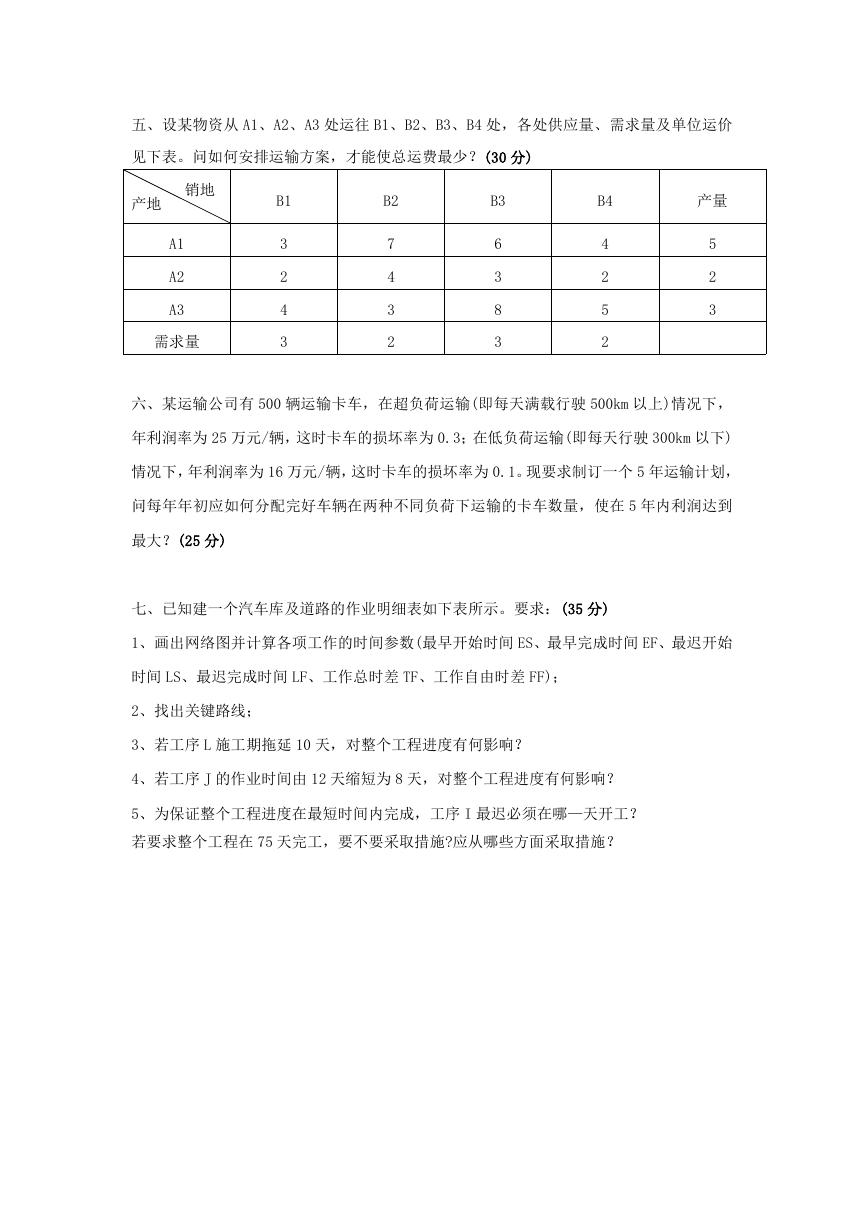
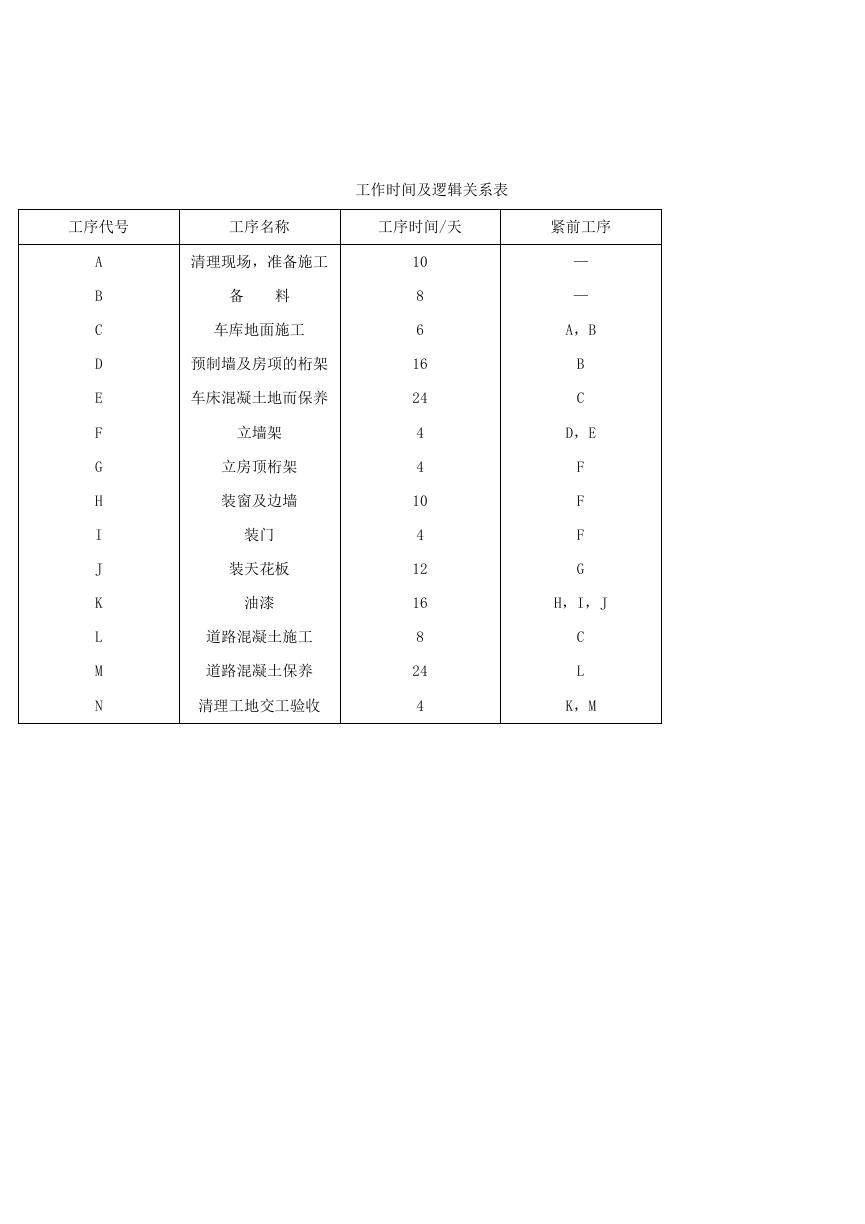
五、设某物资从 A1、A2、A3 处运往 B1、B2、B3、B4 处，各处供应量、需求量及单位运价见下表。问如何安排运输方案，才能使总运费最少？(30 分) 销地产地 A1 A2 A3 需求量 B1 3 2 4 3 B2 7 4 3 2 B3 6 3 8 3 B4 产量 4 2 5 2 5 2 3 六、某运输公司有 500 辆运输卡车，在超负荷运输(即每天满载行驶 500km 以上)情况下，年利润率为 25 万元/辆，这时卡车的损坏率为 0.3；在低负荷运输(即每天行驶 300km 以下) 情况下，年利润率为 16 万元/辆，这时卡车的损坏率为 0.1。现要求制订一个 5 年运输计划，问每年年初应如何分配完好车辆在两种不同负荷下运输的卡车数量，使在 5 年内利润达到最大？(25 分) 七、已知建一个汽车库及道路的作业明细表如下表所示。要求：(35 分) 1、画出网络图并计算各项工作的时间参数(最早开始时间 ES、最早完成时间 EF、最迟开始时间 LS、最迟完成时间 LF、工作总时差 TF、工作自由时差 FF)； 2、找出关键路线； 3、若工序 L 施工期拖延 10 天，对整个工程进度有何影响？ 4、若工序 J 的作业时间由 12 天缩短为 8 天，对整个工程进度有何影响？ 5、为保证整个工程进度在最短时间内完成，工序 I 最迟必须在哪—天开工？若要求整个工程在 75 天完工，要不要采取措施?应从哪些方面采取措施？

工序代号工序名称工序时间/天紧前工序工作时间及逻辑关系表 A B C D E F G H I J K L M N 清理现场，准备施工备料车库地面施工预制墙及房项的桁架车床混凝土地而保养立墙架立房顶桁架装窗及边墙装门装天花板油漆道路混凝土施工道路混凝土保养清理工地交工验收 10 8 6 16 24 4 4 10 4 12 16 8 24 4 — — A，B B C D，E F F F G H，I，J C L K，M

分享到：

赞收藏

资料库

2016年云南昆明理工大学运筹学考研真题A卷.doc

相关推荐

考研

热门标签

最新资料