《光学教程》姚启均答案.pdf-资料库

hechuweijia-1671313-4744302543287521239.pdf-第1页.png

第1页 / 共80页

hechuweijia-1671313-4744302543287521239.pdf-第2页.png

第2页 / 共80页

hechuweijia-1671313-4744302543287521239.pdf-第3页.png

第3页 / 共80页

hechuweijia-1671313-4744302543287521239.pdf-第4页.png

第4页 / 共80页

hechuweijia-1671313-4744302543287521239.pdf-第5页.png

第5页 / 共80页

hechuweijia-1671313-4744302543287521239.pdf-第6页.png

第6页 / 共80页

hechuweijia-1671313-4744302543287521239.pdf-第7页.png

第7页 / 共80页

hechuweijia-1671313-4744302543287521239.pdf-第8页.png

第8页 / 共80页

光学教程（姚启钧原著）参考答案 1

目录第一章光的干涉.....................................3 第二章光的衍射...................................15 第三章几何光学的基本原理...............27 第四章光学仪器的基本原理...............49 第五章光的偏振...................................59 第六章光的吸收、散射和色散...........70 第七章光的量子性...............................73 2

第一章光的干涉 1 . 波长为 nm500 的绿光投射在间距 d 为 cm022.0 的双缝上，在距离 cm180 处的光屏上形成干涉条纹，求两个亮条纹之间的距离.若改用波长为 nm700 的红光投射到此双缝上, 两个亮条纹之间的距离又为多少?算出这两种光第级亮纹位置的距离. 2 解：由条纹间距公式 yy  j 1   ry 0  d j  得 500  10  7  .0 cm409  700  10  7  .0 cm573 409  .0 cm818  2 1 2  1 ry 0  d ry 0  d r j 0 2 d r j 0 2 d y 22 y 22 y  j 2 y 21     180 022 .0 180 022 .0 .02     1  2 y 21   .02 573  .1 cm146  .1 146  .0 818  .0 cm328 2．在杨氏实验装置中,光源波长为 nm640 ,两狭缝间距为 mm4.0 ,光屏离狭缝的距离为 cm50 .试求：(1)光屏上第亮条纹和中央亮条纹之间的距离；（2）若 p 点离中央亮条纹为 1 mm1.0 ，问两束光在 p 点的相位差是多少？（3）求 p 点的光强度和中央点的强度之比. 解：（ 1）由公式 ry 0 d  ry 0 d  50 4.0 = 得  4.6  10  5  0.8  10  2 cm （2）由课本第 20 页图 1-2 的几何关系可知 r r d 2   1 sin 0.8 10 cm  5    d tan   d y r 0  0.04 0.01 50  3

   2   r r ( ) 2 1   2  6.4 10   5  0.8 10   5   4 (3) 由公式 I A A AA 2    2 2 1 2 2 1 cos    4 A 2 1 2 cos   2 得 I p I 0  A 2 p A 2 0 1   cos 2   4 4 A 2 1 2 cos 4 A 2 1 2 cos   2   0 2 2 cos cos  1  42 0 2    2 cos  8 2  2  4  .0 8536 3 . 把折射率为 1.5 的玻璃片插入杨氏实验的一束光路中,光屏上原来第 5 级亮条纹所在的位置为中央亮条纹,试求插入的玻璃片的厚度.已知光波长为 6×10-7m. 解：未加玻璃片时，、到点的光程差，由公式 1S 2S P r   2    可知为 r r    2  2 1 Δr = 5 2      5 现在发出的光束途中插入玻璃片时，点的光程差为 P 1S r h nh   2        1   r 2       2    0 0 所以玻璃片的厚度为 h  r r  2 1 n 1   5  0.5  10    6 10 cm  4 4. 波长为 500nm 的单色平行光射在间距为 0.2mm 的双狭缝上.通过其中一个缝的能量为另一个的 2 倍,在离狭缝 50cm 的光屏上形成干涉图样.求干涉条纹间距和条纹的可见度. ry   0 d   解： 500 500 10 0.2    6  1.25 mm 22I I 1 22A A 2 2 1 A 1 A 2  2 4

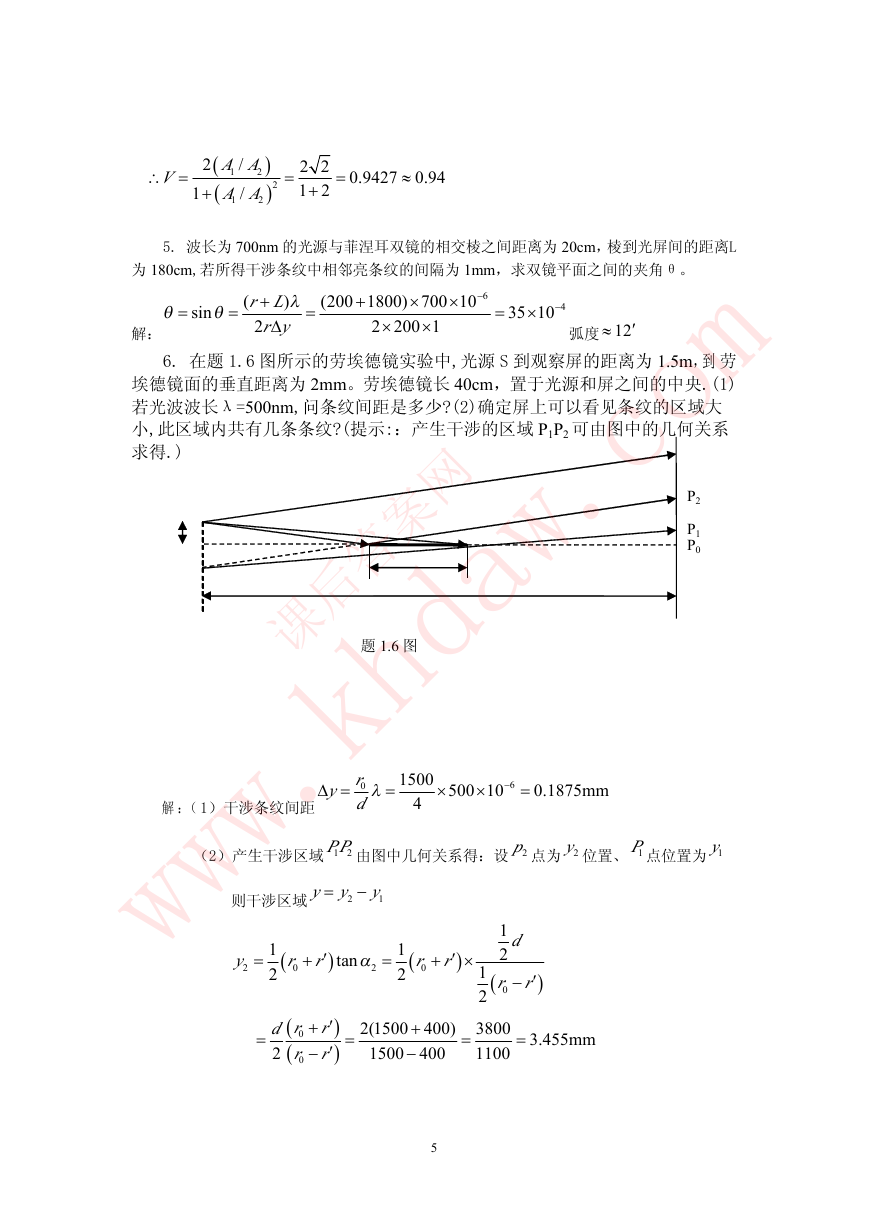
  V 2    A A 1 2 A A 1 2 / /   2 1  2 2 1 2   0.9427  0.94 5. 波长为 700nm 的光源与菲涅耳双镜的相交棱之间距离为 20cm，棱到光屏间的距离L 为 180cm,若所得干涉条纹中相邻亮条纹的间隔为 1mm，求双镜平面之间的夹角θ。   sin   r L ) (   r y 2   解： (200 1800) 700 10    2 200 1   6   35 10   4 弧度  12 6. 在题 1.6 图所示的劳埃德镜实验中,光源 S 到观察屏的距离为 1.5m，到劳埃德镜面的垂直距离为 2mm。劳埃德镜长 40cm，置于光源和屏之间的中央.(1) 若光波波长λ=500nm,问条纹间距是多少?(2)确定屏上可以看见条纹的区域大小,此区域内共有几条条纹?(提示:：产生干涉的区域 P1P2 可由图中的几何关系求得.) P2 P1 P0 题 1.6 图解：（ 1）干涉条纹间距 ry   0 d   1500 500 10 4   6   0.1875mm （2）产生干涉区域 1 2PP 由图中几何关系得：设点为位置、点位置为 2p 2y 1P 1y 则干涉区域 y y y 1   2 y 2  1 2  r r 0    2 tan  1 2  r r  0     d 2   r r  0 r r  0    2(1500 400) 1500 400    5 d 1 2 r r  0   1 2 3800 1100  3.455mm

d 1 2 r r ) (  0  r r d ( )  0 r r 2 ( )  0  r r ( ) 1  0 2 y 1  1 2 r r ) tan (  0   1  1 2 2(1500 400) 1.16mm 1500 400     y y y 1   2  3.46 1.16   2.30mm （3）劳埃镜干涉存在半波损失现象   y y  N 暗 7. 试求能产生红光(λ=700nm)的二级反射干涉条纹的肥皂膜厚度.已知肥皂膜折射率为 1.33,且平行光与发向成 30°角入射. 解：根据题意 2 2  d n n 2 2  1 (2 d   2 2  2 sin  j 1)   n n 2 2  2 1 (2 j   2 sin 10) 2  (2 2 1) 700    sin 30 4 1.33  2 2  710nm  8. 透镜表面通常镀一层如 MgF2（n=1.38）一类的透明物质薄膜，目的是利用干涉来降低玻璃表面的反射．为了使透镜在可见光谱的中心波长（550nm）处产生极小的反射,则镀层必须有多厚? 解：可以认为光是沿垂直方向入射的。即 1 ii  2 0  由于上下表面的反射都由光密介质反射到光疏介质，所以无额外光程差。因此光程差  nh 2 cos i 2  nh 2 如果光程差等于半波长的奇数倍即公式 r  2( j  )1  2 ，则满足反射相消的条件 nh 2  2( j  )1  2 h  2(  j )1  n 4 ( j  ,1,20  ) 因此有所以 0j 当时厚度最小 h min   n 4  550 38.14   nm64.99  10 5- cm 9. 在两块玻璃片之间一边放一条厚纸,另一边相互压紧.玻璃片 l 长 10cm,纸厚为 0.05mm,从 60°的反射角进行观察,问在玻璃片单位长度内看到的干涉条纹数目是多少?设单色光源波长为 500nm. 解：由课本 49 页公式（1-35）可知斜面上每一条纹的宽度所对应的空气尖劈的厚度的 6

hh  j 1   h j   nn 2 2  1 2 2 2 sin i 1 变化量为    12      2 3 2    如果认为玻璃片的厚度可以忽略不记的情况下，则上式中 nn 2 2   i ,1 1  60 。 而厚度 h 所对应的斜面上包含的条纹数为 hN h    h   05.0 10  5000 7   100 故玻璃片上单位长度的条纹数为 NN  l  100 10  10 条/厘米 10. 在上题装置中,沿垂直于玻璃片表面的方向看去,看到相邻两条暗纹间距为 1.4mm。 —已知玻璃片长 17.9cm,纸厚 0.036mm,求光波的波长。 i 解:依题意,相对于空气劈的入射角 2  0,cos i 2  1.sin   tan  d L 2 n 0.1   2   L  d 2 i 2 L     n cos 2  2 Ld 2  L   .02  036 179  4.1  .5 631284916  10  4 mm  563.13nm 11. 波长为 400 760nm 的可见光正射在一块厚度为 1.2×10-6m,折射率为 1.5 玻璃片上,试问从玻璃片反射的光中哪些波长的光最强. 解：依题意，反射光最强即为增反膜的相长干涉，则有：   dn 2 2  2( j  )1  2   dn 4 2 j 2 1  故时，0j 当 dn  4 2  2.15.14   10  3  7200 nm 时，1j 当   2.15.14    10  3 3  2400 nm 时，2j 当   2.15.14    10  3 5  1440 nm 7

时，3j 当   2.15.14    10  3 7  1070 nm 时，4j 当   2.15.14    10  3 9  nm800 时，5j 当   2.15.14   11  10  3  654 nm5. 时，6j 当   2.15.14   13  10  3  553 nm8. 时，7j 当   2.15.14   15  10  3  nm480 时，8j 当   2.15.14   17  10  3  423 nm5. 时，9j 当   2.15.14   19  10  3  nm378 所以，在 390 ~ nm760 的可见光中，从玻璃片上反射最强的光波波长为 423 ,nm5. 553,nm480 ,nm8. 654 5. nm. 12. 迈克耳孙干涉仪的反射镜 M2 移动 0.25mm 时，看到条纹移过的数目为 909 个，设光为垂直入射，求所用光源的波长。解：根据课本 59 页公式可知，迈克耳孙干涉仪移动每一条条纹相当 h 的变化为： hhh  1  2    j 1   i cos 2 2  j  i cos 2 2   cos 2 i 2 2 i 0 现因，故 h  2 N 909 所对应的 h 为 NhNh  2   h 2 N  25.02  909 故  5.5  10  4 mm  550nm 13. 迈克耳孙干涉仪平面镜的面积为４×４cm2，观察到该镜上有 20 个条纹。当入射光的波长为 589nm 时，两镜面之间的夹角为多大？解：因为 cm44 S 2 8

资料库

《光学教程》姚启均答案.pdf

相关推荐

课程资源

热门标签

最新资料