异步电动机直接转矩控制基本原理.doc-资料库

qq375629943-9328809-4744302543439032956.doc.pdf-第1页.png

第1页 / 共18页

qq375629943-9328809-4744302543439032956.doc.pdf-第2页.png

第2页 / 共18页

qq375629943-9328809-4744302543439032956.doc.pdf-第3页.png

第3页 / 共18页

qq375629943-9328809-4744302543439032956.doc.pdf-第4页.png

第4页 / 共18页

qq375629943-9328809-4744302543439032956.doc.pdf-第5页.png

第5页 / 共18页

qq375629943-9328809-4744302543439032956.doc.pdf-第6页.png

第6页 / 共18页

qq375629943-9328809-4744302543439032956.doc.pdf-第7页.png

第7页 / 共18页

qq375629943-9328809-4744302543439032956.doc.pdf-第8页.png

第8页 / 共18页

异步电机动直接转矩控制基本原理异步电动机直接转矩控制基本原理从 1985 年德国鲁尔大学德彭布洛克（Depenbrock）教授首次提出直接转矩控制理论以来，短短十几年时间，直接转矩控制理论以它简明的系统结构，优良的静、动态性能得到迅猛发展和应用。 1 异步电动机的数学模型异步电机数学模型是一个高阶、强耦合、多变量、非线性系统。理想状态下（一般这样假设）电机三相（定、转子）均对称，定、转子表面光滑，无齿槽效应，电机气隙磁势在空间正弦分布，铁心涡流、饱和及磁滞损耗不计。在固定坐标系下（，，0），用异步电机转子的量来表示异步电机数学模型（则有 ru ＝ ru ＝0）。基本方程如下：        （1）（2）（3） u  s   u  s   0  0         T e  n p         R  s  0 . L  . L s m L m s 0 . R L  s L  . L m m . L m 0  R r   r . L L r 0 . L m L   r r . L R         r s  i  s   i   i r   i   r  (    s  i i s s  s )  ( iLn mp i s r   i i r  s ) Jd  dtn p  T e  TL  F  n p sR 、 sL ：定子电阻和自感 rR 、 rL ：转子电阻和自感 mL ：定子互感 ：电机转子角速度，即机械角速度 su 、 su ：定子电压（、）分量 si 、 si ：定子电流（、 ）分量

异步电机动直接转矩控制基本原理 ru 、 ru ：转子电压（、）分量 ri 、 ri ：转子电压（、）分量 J ， F 分别为机械转动惯量和机械磨擦系数本文均采用空间矢量分析方法，图 1 是异步电机的空间矢量等效图，在正交定子坐标系（  坐标系）下描述异步电机模型。 is Rs su L ui .  s L ri .  r R r j r 图 1 异步电动机空间矢量等效图各个物理量定义如下： )(tus —定子电压空间矢量 )(t is —定子电流空间矢量 )(t ir —转子电流空间矢量 )(ts —定子磁链空间矢量  —电角速度依图 1 以下表达式表示异步电机在定子坐标系下的方程： U s  iR ss  s 0 = rriR - r +j r s =L ui r = s - riL (5) (4) (6) (7) 定子旋转磁场输出功率为（下式 s 表示定子旋转磁场的频率）： P= dsT = 3 2 RE  ssi { *} = 3 2 (   i i    s s   s ) (8) s .  ＝并且有 s j  s ( iL s  ji ) s  (9)

异步电机动直接转矩控制基本原理把表达式(9)分解到（  ）坐标下得： .  s  .  s    s Li s    s Li s    s  s   s  s 把式（10）和式（11）代入式（8）得转矩表达式： T d  3 2 ( i i    s s   s s ) （10）（11）（12）从图 1 可得： i s  i u  i r T d  31 2 L  ，结合式（6）、式（7）得： ( i  s r  )   r s  （13）上式也可以表示成（为磁通角，即定子磁链与转子磁链之间的夹角）： T  d 31 2 L   sin r s （14）定子磁链的幅值根据式（4）由定子电压积分来计算的，而转子磁链幅值由负载决定的，它根据式（5）由转子电流决定，而稳态转矩据式（14）则通过计算磁通角来实现。 2 电压型逆变器的模型逆变器是直接转矩伺服驱动器中的重要部分，本系统采用的是电压型逆变器。如图 2，每个桥臂各有上、下两个开关管（ aS 、 bS 、 cS 、  aS 、  bS 、  cS ），在同一时刻总有一个开关管断开，另一个闭合。其中 aS 与  aS ， bS 与  bS cS 与  cS 均互为反向，也即一个导 2E 通而另一个断开。a、b、c 表示异步电机的三相。逆变器总共有 8 种开关状态，如表 1： aS bS cS  aS  bS  cS a b c 图 2 电压型逆变器

异步电机动直接转矩控制基本原理表 1 逆变器 8 种开关状态开关状态 aS bS cS 0 0 0 0 1 1 0 0 2 0 1 0 3 1 1 0 4 0 0 1 5 1 0 1 6 0 1 1 7 1 1 1 从表 1 可以看出，开关状态 0、7 属于同一状态，其相当于把电机三相 A、B、 C 同时接到同一电位上，这两种状态称为零状态；而另外状态 1～6 则称为工作状态。所以实际上电压逆变器共有 7 种不同状态。由图 2 可知，当电压型逆变器在没有零电平输出时它的六种工作状态的电压波形、电压幅度和开关状态的对应关系如图 3，图中 1su 、 2su 、 3su 、 4su 、 5su 、 6su 分别对应状态（011）、（001）、（101）、（100）、（110）、（010）。 au bu cu 2 3 ud  4 3 E 1 3 ud  2 3 E t t t abcS )(tus 011 001 101 100 110 010 1 1su 2 2su 3 3su 4 4su 5 5su 6 6su 图2-3 工作状态三相电压波形

异步电机动直接转矩控制基本原理把逆变器的输出电压用空间矢量来表示，电压空间顺序见图 4。 )(tut 表示电压矢量，则 7 有个离散的电压空间矢量。每个工作电压空间矢量在空间位置相差 60°，矢量以逆时针顺序旋转，即顺序为 1su → 2su → 3su → 4su → 5su → 6su 。其中六边形的中心是零电压矢量。对异步电机三相分析，将三维矢量转化为二维矢量，在这用 Park 变换。将异步电机三相定子坐标系的轴与 Park 矢量复平面的实轴重合，则三相物理量 )(tX a 、 )(tX b 、 )(tX c 的 Park 矢量 )(tX 为： )(tX ＝ 2 [ 3 )(tX a +  )(tX b + 2 )(tX c ] 120 其中 ＝  je 。 ) 110(5su 5 100(4su ) 4 6 6su 010 ( ) 000 111 7 )(tus 3 3su )101( 1 )011(1su 2 (2su )001 图2-4 六边形电压空间矢量（15）由图 2 的接法，其输出电压空间矢量 )(tus 的 Park 矢量变换表达式为： )(tus ＝ 2 [ au ＋ 3 beu 3/2j + ceu 3/4j ] （16） au 、 bu 、 cu 分别是 a、b、c 三相定子负载绕组的相电压。依图 3 给出的 au 、 bu 、 cu 并代入式（16）可以计算出从 1～6 各个状态输出的电压空间矢量 )(tus 。直接转矩控制是根据定子磁链 s ，转矩 eT 的要求，从 1～7 状态中选出一个最佳控制矢量使电机运行在特定的状态。 3 磁链控制磁链控制的任务是识别磁链的运动轨迹的区段或位置，给出正确的磁链开关信号，以产生相应的电压空间矢量，控制六边形轨迹或圆形轨迹正确地旋转。

异步电机动直接转矩控制基本原理 3.1 磁链轨迹的控制由式（4）可得： )( t s   ( )( tu s  i s )( Rt s ) dt 如果忽略 sR 则式（17）可表示成  )( t s )( tu s dt （17）（18）由式（18）可以看出电机定子磁链 s 的运动方向是依 )(tus 方向进行的。当电压逆变器开关状态不发生变化时，定子电压矢量不变，此时电机采用非零空间电压矢量，则 s 的运行方向与幅值将发生变化；但当采用零电压矢量时 s 的运行将受到抑制。按照状态 1su → 5su → 4su → 6su → 2su → 3su 顺序运行一周后，将形成一个六边形磁链轨迹，如图 4。而合适地施加非零矢量顺序和合理的作用时间比例，可以形成一个多边形磁链轨迹，以致近似圆形轨迹。把（  ）复平面分成 6 个区域，如图 5， 2(  )3 N  (  N )  6  2( N )1   6 N ＝1，2，3，4，5，6 （19）假设测得的定子磁链为 s ，给定磁链为 sref ，将 s 与 sref 之间的偏差进行滞后比较，当误差不在所允许的范围之内时就进行电压切换，以减小误差。实现这种功能的环节称为磁链调节器，实际上它是一个施密特触发器。图 6 为磁链调节器的功能图。图中 Y 为磁链调节器的输出，  为磁链误差带宽。当 sref － s   2 时，磁链调节器输出 Y ＝1，即选择电压矢量使 s 增加。  )2( )3( )4( )5( )6( )1(  图 5 圆形磁链轨 Y 1 sref   s   2  2 图 6 磁链调节器

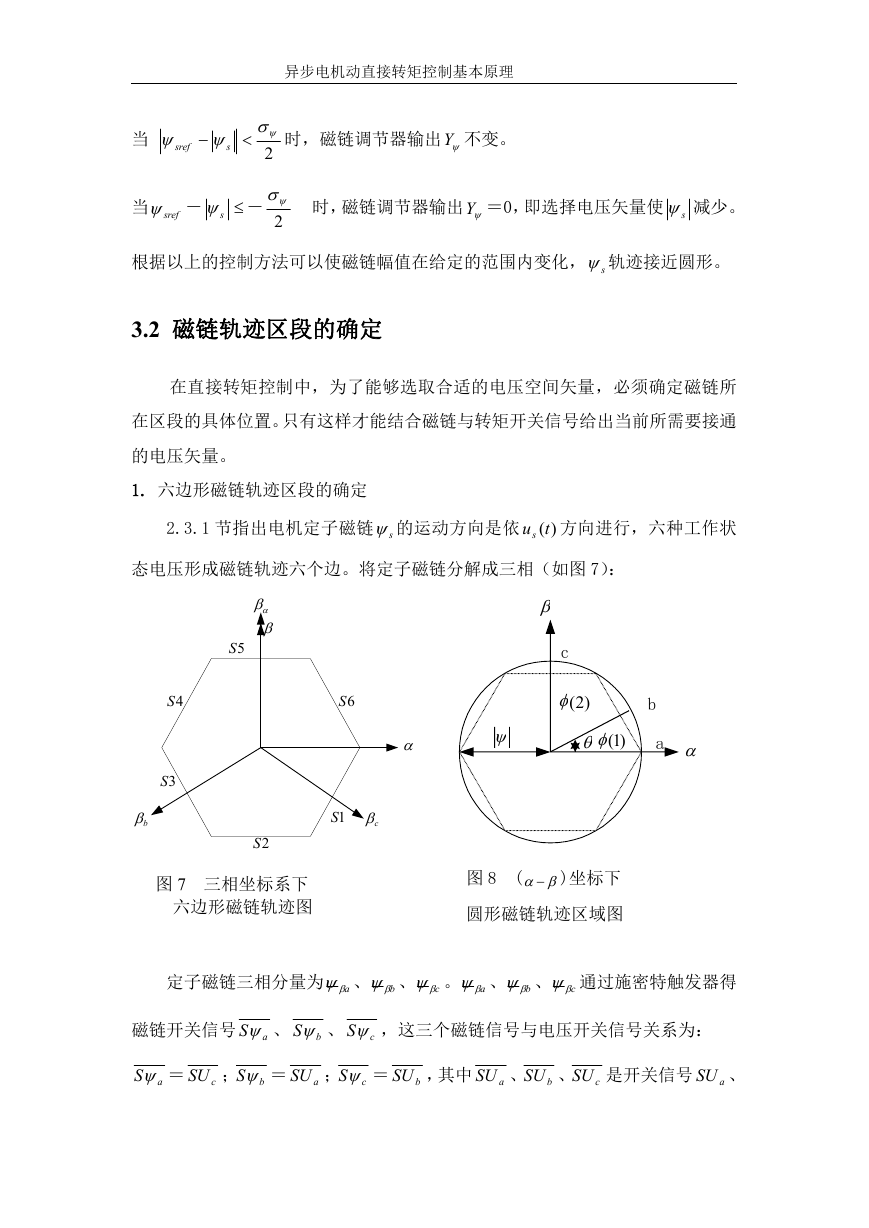
异步电机动直接转矩控制基本原理当   s sref   2 时，磁链调节器输出 Y 不变。当 sref － s  －  2 时，磁链调节器输出 Y ＝0，即选择电压矢量使 s 减少。根据以上的控制方法可以使磁链幅值在给定的范围内变化， s 轨迹接近圆形。 3.2 磁链轨迹区段的确定在直接转矩控制中，为了能够选取合适的电压空间矢量，必须确定磁链所在区段的具体位置。只有这样才能结合磁链与转矩开关信号给出当前所需要接通的电压矢量。 1. 六边形磁链轨迹区段的确定 2.3.1 节指出电机定子磁链 s 的运动方向是依 )(tus 方向进行，六种工作状态电压形成磁链轨迹六个边。将定子磁链分解成三相（如图 7）：   5S 6S 4S 3S b 1S c 2S 图 7 三相坐标系下六边形磁链轨迹图  c )2( b    )1( a  图 8 (  )坐标下圆形磁链轨迹区域图定子磁链三相分量为 a 、 b 、 c 。 a 、 b 、 c 通过施密特触发器得磁链开关信号 aS 、 bS 、 cS ，这三个磁链信号与电压开关信号关系为： aS ＝ cSU ； bS ＝ aSU ； cS ＝ bSU ，其中 aSU 、 bSU 、 cSU 是开关信号 aSU 、

异步电机动直接转矩控制基本原理 bSU 、 cSU 的反相。定子磁链与六边形区段对应关系如表 2：表 2 定子磁链与六边形区段对应关系表（ a ， b ， c ）（011）（001）（101）（100）（110）（010）磁链区段 1S 2S 3S 4S 5S 6S 2．圆形磁链轨迹区段的确定圆形磁链轨迹磁链幅为： 2   s    2 s ， s ， s 为定子磁链在（坐标  ）下的投影。如图 8 将圆形轨迹分成六个区域，根据 s ， s 的正负值可以确定磁链轨迹在哪个区域中。；例如在第一象限，＝30°，在 ab 弧≤30°，而在 bc 弧段≥30°。通过这种方式可以确定磁链在圆形轨迹的任何一个区域。 4 转矩控制从式（14）可知，异步电机的转矩由定、转子磁链的幅值、磁通角决定的。而转子磁链幅值由负载决定的。为了充分利用电机铁芯，保持定子磁链为恒量。改变转矩可以通过磁通角来实现，即通过改变电压空间矢量 )(tus 来控制定子磁链旋转速度，使其走走停停，以达到改变定子磁链的平均速度 s ，从而实现改变磁通角，最后达到控制转矩的目的。这个过程可以用图 9 来解释。 1t 时 110(5su )  6S  100(4su ) 5S 0s ) ( 000 )111( )101(3su 刻定子与转子磁链分别为 ( 1ts 、 ) ( 1tr ，磁通角为 ) ( 1t ，从 1t 运 ) 行到 2t 时刻，此时对定子所加的电压空间矢量 )(tus 为 )101(3su ， (6su 010 ) 定子磁链从位置 ( 1ts 到位置 ) ( 2ts 所运行的轨迹为 s ， ) 轨迹方向与 )101(3su 所指的方向一致，而且沿着 3S 。由式子：0= 1S 2S s ( 1tr ) ( 1t ) ( 2ts ) ( 2tr ) ( 2t ) )011(1su (2su 3S )( 1ts s 图 9 电压空间矢量对电机转矩的影响 4S )001 rriR - r +j r 可知在此运行期间转子磁链不

资料库

异步电动机直接转矩控制基本原理.doc

相关推荐

开发技术

热门标签

最新资料