开关磁阻电机的MATLAB仿真建模研究.pdf-资料库

http://www.paper.edu.cn 开关磁阻电机的 MATLAB 仿真建模研究闫荣超河海大学电气工程学院，南京（210098） E-mail: rcyan1982@yahoo.com.cn 摘要：开关磁阻电动机调速系统(Switched Reluctance Drive,简称 SRD),具有启动转矩大、调速范围宽及运行效率高的特点。本文在分析开关磁阻电机数学模型的基础上，借助于 MATLAB/SimPowerSystems 工具箱，对一台 6/4 三相开关磁阻电机进行建模和仿真。在分析开关磁阻电机（SRM）数学模型的基础，建立独立的功能模块，如电机本体模块、速度控制模块、电流控制模块、转角选择模块等，再进行功能模块的有机整合，搭建 SRM 控制系统的仿真模型。系统采用双闭环控制：速度环采用 PID 控制，电流环采用电流斩波控制的方法，保证了 SRM 在低速或高速运行时都可获得满意的性能。仿真结果证明了该 SRM 建模方法的合理性、有效性。关键词：开关磁阻电机；MATLAB；动态模型中图分类号: TM35 文献标识码: A 1. 引言 80 年代，在交流调速技术得到了迅猛的发展情况下一种新型的交流调速电动机——开关磁阻电机（Switched Reluctance Motor,简称 SRM）诞生了。因 SRM 具有机构简单、坚固，工作可靠，效率高，价格低、适应力强等优点，由其构成的调速系统——开关磁阻电机调速系统（SRD）得到了比较广泛的应用。然而，由于 SRD 具有严重非线性及变结构、变参数、数学模型难以准确建立的特点，如何建立有效的 SRM 控制系统仿真模型成为当前开关磁阻电机研究的重要课题。针对 SRM 内部磁场非线性、非线性开关电源供电、相电流波形难以解析等特点，SRM 的分析、设计、控制方法的研究与讨论一直是近年来的热点问题。W.H.Koch 等最先提出了线性化模型，并在此基础上分析了电机结构参数与电机性能之间的关系[4]，但线性化模型忽略了电机内部的非线性特性，在电机性能的预测上由较大误差。本文在非线性电感模型近似解析式的分析基础上 ,利用 MATLAB 将系统各单元模块化,再将这些模块有机结合,即可搭建出开关磁阻电机系统的非线性模型。因此本文所建立的模型可以扩展成任意相开关磁阻电机系统的仿真模型,为分析和设计开关磁阻电机控制系统提供了有效的手段。本文以 6/4 三相电机为例建立了开关磁阻电机的仿真模型。 2. SRM 的数学模型对于 m 相 SRM，若不计磁滞、涡流、及绕组间互感时，系统示意图如图 1 所示：图中，Ｊ为 SRM 转子及负载的转动惯量，D 代表粘性摩擦系数，TL 表示负载转矩。描述此图的微分方程由电路方程、机械方程、机电联系方程三部分组成[1]。 - 1 -

http://www.paper.edu.cn 图 1 m 相 SRM 系统示意图 2.1 电路方程电机第 k 相电压平衡方程式为： iR kk U = /ψ+ k d dt 式（1）式（1）中，Uk 为加于第 k 相绕组的电压，Rk 为 k 相绕组的电阻，ik 为 k 相绕组的电 Ψk k 为 k 相绕组的磁链。一般说来，Ψk 是绕组电流 ik 和转子位置角 θ 的函数，即： ( θψψ ) = , i k k k 式（2）电机的磁链可用电感和电流的乘积来表示，即： ψ k = iL ) ( θ k , ⋅ i k 式（3）将式（3）代入式（1）得：式（4） U = iR kk + k 式 (4) 表明，电源电压与电路中的三部分电压降相平衡。其中，等式右边第一项为第 k 相回路中的电阻压降；第二项是由电流变化引起磁链变化而感应的电动势，称为变压器电动 dL ∂ θ k dt θ∂ L ∂ i ∂ iR kk + + + = i i k k k ∂ ψ k i ∂ ⎛ ⎜⎜ ⎝ L k di k dt + d θ dt ψ ∂ k θ ∂ di ⎞ k ⎟⎟ dt ⎠ k k 势；第三项是由转子位置改变引起绕组中磁链变化而感应的电动势，称为运动电动势，它与电磁机械能量转换直接有关。 2.2 机械方程按照力学定律可列出在电机电磁转矩 Te 和负载转矩 TL 作用下的转子机械运动方程： T e = J d 2 θ dt 2 + f d θ dt + T L 式（5） J 为转动惯量，f 为摩擦系数。 2.3 机电联系方程根据机电能量转换的基本原理，当 A 相绕组通以电流 i 时，在转子上产生的电磁转矩 T （θ，i）可以由下式表示： - 2 -

http://www.paper.edu.cn T i ( , ) θ = W ∂ i ' ( , ) θ θ ∂ = i ∫ 0 i ( , ) ψθ ∂ θ ∂ di 式（6） 3. 基于 MATLAB/SimPowerSystems 的开关磁阻电机调速系统建模本文结合实验样机的参数采用模块化方式建立三相（6/4）SRM 调速系统动态仿真模型。由 SRD 的结构特点，将 SRD 的仿真模型分成三部分，即控制电路、功率变换器和电机本体。其原理图如下，图 2 SRM 调速系统原理图利用 SimPowerSystem Toolbox 丰富的模块库，在分析 SRM 数学模型的基础上，建立了 SRM 控制系统的仿真模型，整体设计框图如图 3 所示。系统采用双闭环控制方案：转速环由 PID 调节器构成，电流环由角位置控制器与电流斩波控制器复合构成。根据模块化建模的思想，将控制系统分割为各个功能独立的子模块，主要包括：SRM 本体模块、速度控制模块、电流控制模块、转角选择模块、参数计算模块、转矩计算模块和电压逆变模块。通过这些功能模块的有机整合，就可在 Matlab/Simulink 中搭建出 SRM 控制系统的仿真模型，并实现双闭环的控制算法，图 3 中各功能模块的作用与结构简述如下。 TL TL jiaoduin A+ A- B+ B- C+ C- theta Speed1 current Te SRM Scope Continuous pow ergui Step theta jiaoduout PID current1 current Pulse CONTROL DC pulse V+ V- A+ A- B+ B- C+ C- CONVERTER 图 3 SRD 仿真框图 - 3 -

http://www.paper.edu.cn 3.1 控制电路模块 1 theta jiaoduin jiaoduout 角度计算 1 jiaoduout 2 current1 Saturation 3 current Add Add1 Add2 thetaa currenta PWMa phase a pulse thetab currentb PWMb phase b pulse thetac currentc PWMc phase c pulse 图 4 SRD 控制电路模块 2 Pulse 图中角度计算模块是计算各相转子位置及转子与相对应定子的相对位置角度，此模块主要包含 3 个 MatlabFunction,分别对应 SRM 的 3 个相，将反馈的转子旋转角度，经过处理归宿安慰一个转子极矩角内对应的参考零角度的值。PWM 信号发生模块 a 相仿真电路如下 1 currenta 5 alfa 35 beta 2 w Relay AND >= <= 1 PWMa Product 图 5 PWM 信号发生模块 Alfa、beta 分别为开关磁阻电机的开通角和关断角，参考角度经过与模块处理后输出一个高/低电平信号，以便控制经过滞环调节的信号的输出。 3.2 功率变换器功率变换器采用不对称半桥电路搭建仿真模型，如图 6 所示， 1 V+ 1 pulse em 2 V- G C1 V+ C2 V- BR_CONV1 G C1 V+ C2 V- BR_CONV2 G C1 V+ C2 V- BR_CONV3 3 A+ 4 A- 5 B+ 6 B- 7 C+ 8 C- 1 V+ 1 G 2 V- g C IGBT E D 3 C1 4 C2 D1 IGBT1 g C E 图 6 PWM 信号模块图 7 一相子模块该不对称半桥电路由 SimPowerSystems 中的元件（直流电压源、电容、IGBT、电力二 - 4 -

http://www.paper.edu.cn 极管等）连接而成。控制信号由控制电路产生，控制可控器件 IGBT 的通断。图 4 为与 a 相绕组相连的功率变换电路。V+、V-接开关管的额定电压，由于主开关管的电压定额与电动机的绕组的电压定额近似相等，所以这种线路用足了主开关管的额定电压，有效的全部电源电压可用来控制相绕组电流。 3.3 电机本体模块根据 SRM 的电压方程、转矩方程和机械方程等，搭建了开关磁阻电机仿真模型，如图 5 所示， 2 jiaoduin emu theta torquea ia A+ A- phaseA thetb torqueb ib B+ B- phaseB thetc torquec ic C+ C- phaseC 1 A+ 3 B+ 5 C+ 2 A- 3 current 4 B- 6 C- 1 TL 1/J 1 s moment of inertia Integrator friction D 图 8 SRM 仿真模型 4 Te 1 s Integrator1 1 theta -K- Gain1 2 Speed1 图 8 中的引脚 A+、A-、B+、B-、C+、C-与功率变换器连接，模块 Phase A, Phase B, Phase C 分别代表 SRM 的三个相，torquea、torqueb、torquec 为每一相的输出转矩，相加后得到合成转矩，模块 TL 为负载转矩。 4. 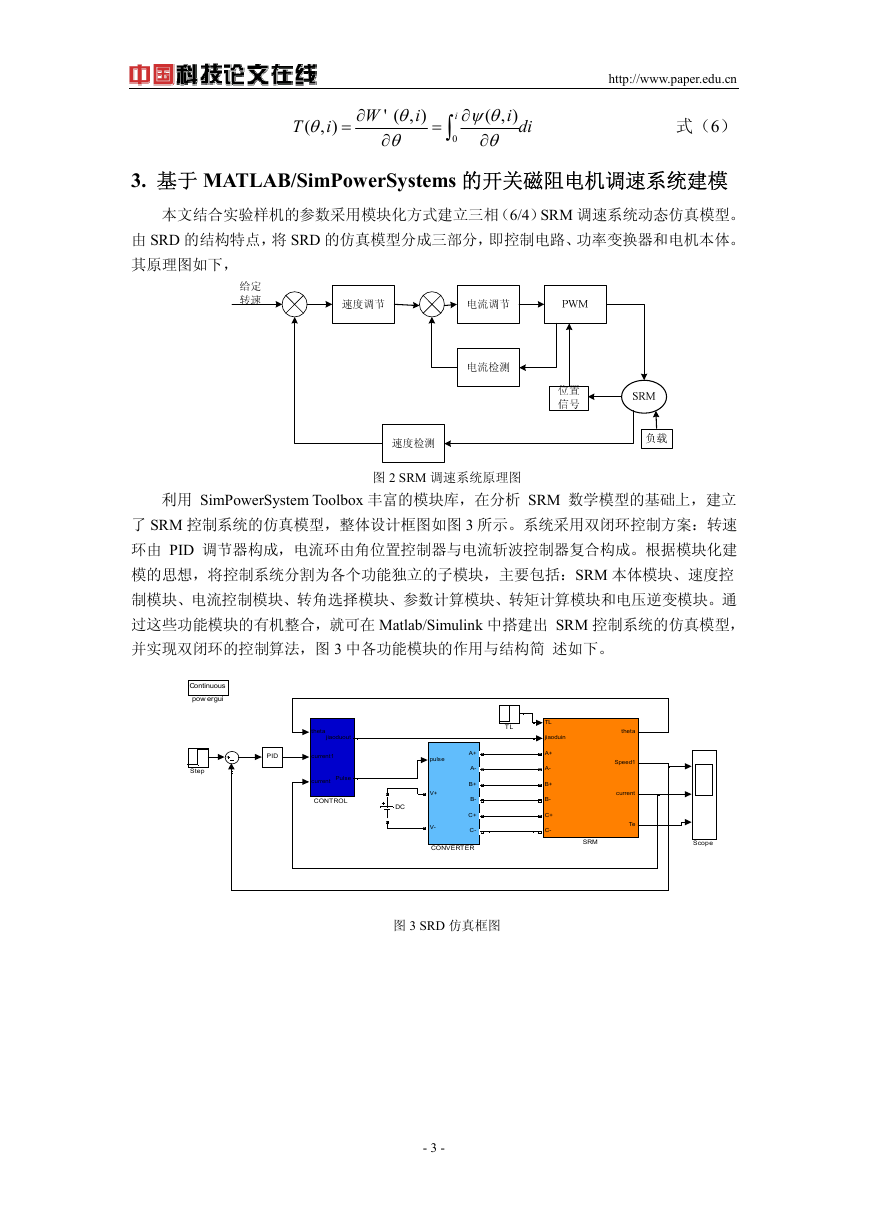仿真结果本文研究的实验样机是一台三相（6/4 极）SRM，其电磁特性如图 9、10 所示，技术参数为：额定功率：750W,额定电压：220V,定子极数：6, 转子极数：4,定子极弧：30o,转子极弧：32o,相绕组：1.27 欧,最大相电感：0.1826H,最小相电感：0.0108H,转动惯量：0.0017 kg*m 2 。图 9 三相（6/4 极）SRM 样机转矩-电流-角度特性 - 5 -

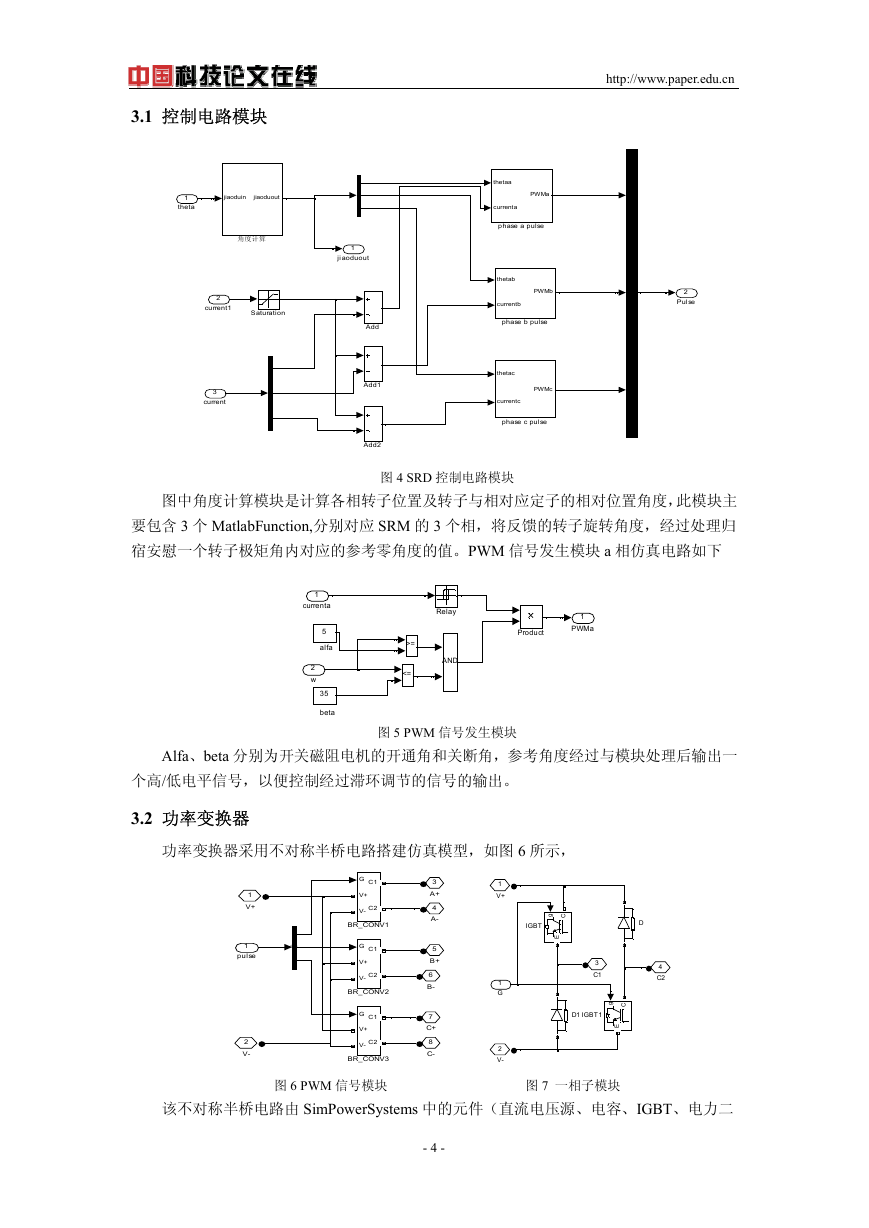
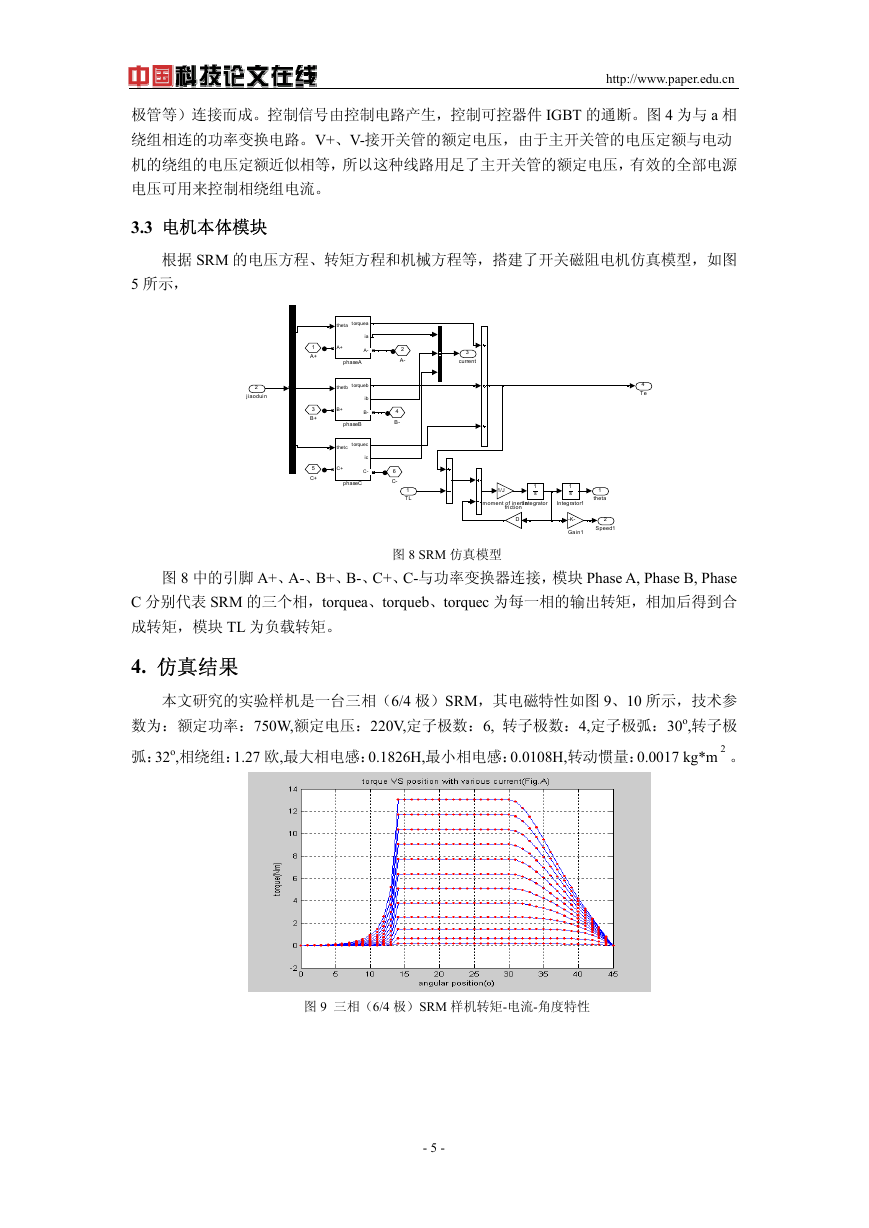
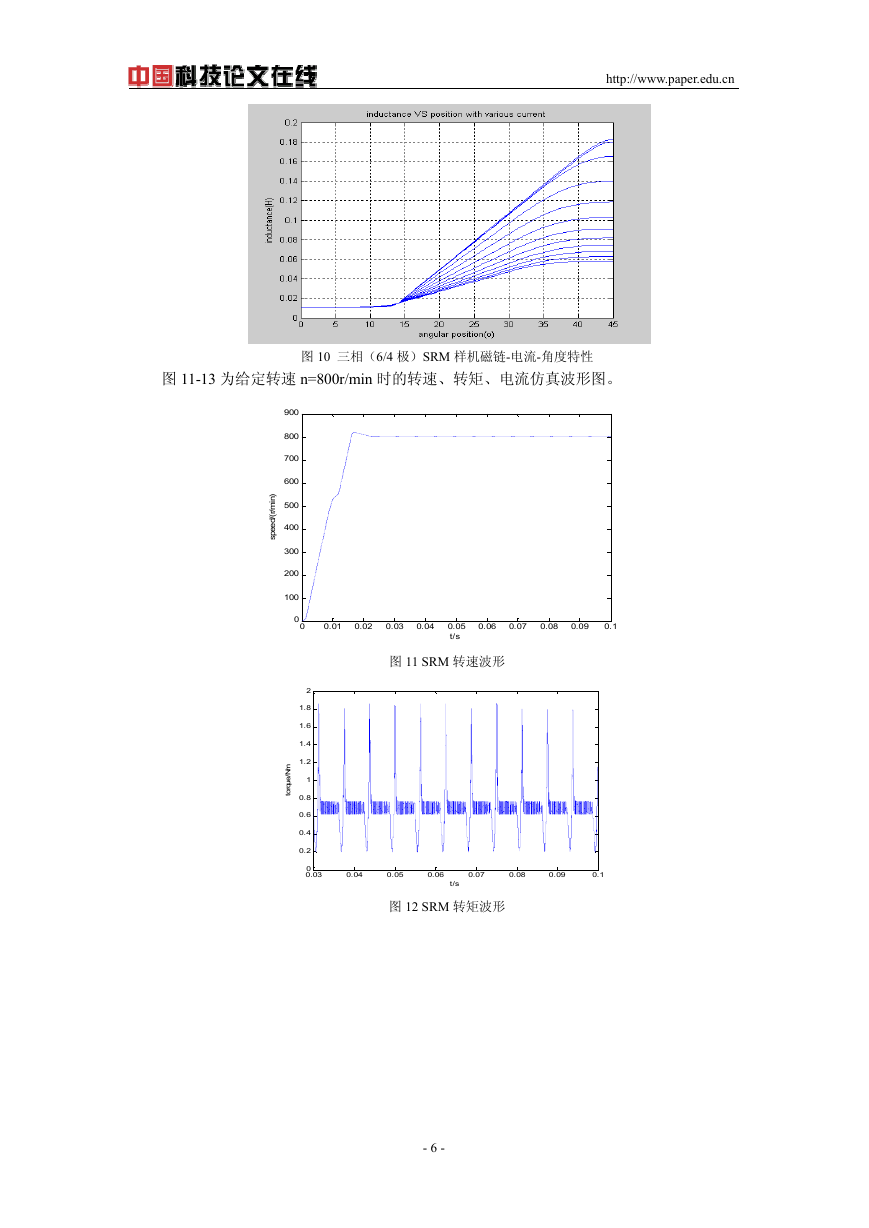
http://www.paper.edu.cn 图 11-13 为给定转速 n=800r/min 时的转速、转矩、电流仿真波形图。图 10 三相（6/4 极）SRM 样机磁链-电流-角度特性 900 800 700 600 500 400 300 200 100 ) n mi / r ( / d e e p s / m N e u q r o t 0 0 0.01 0.02 0.03 0.04 0.06 0.07 0.08 0.09 0.1 0.05 t/s 图 11 SRM 转速波形 2 1.8 1.6 1.4 1.2 1 0.8 0.6 0.4 0.2 0 0.03 0.04 0.05 0.06 0.07 0.08 0.09 0.1 t/s 图 12 SRM 转矩波形 - 6 -

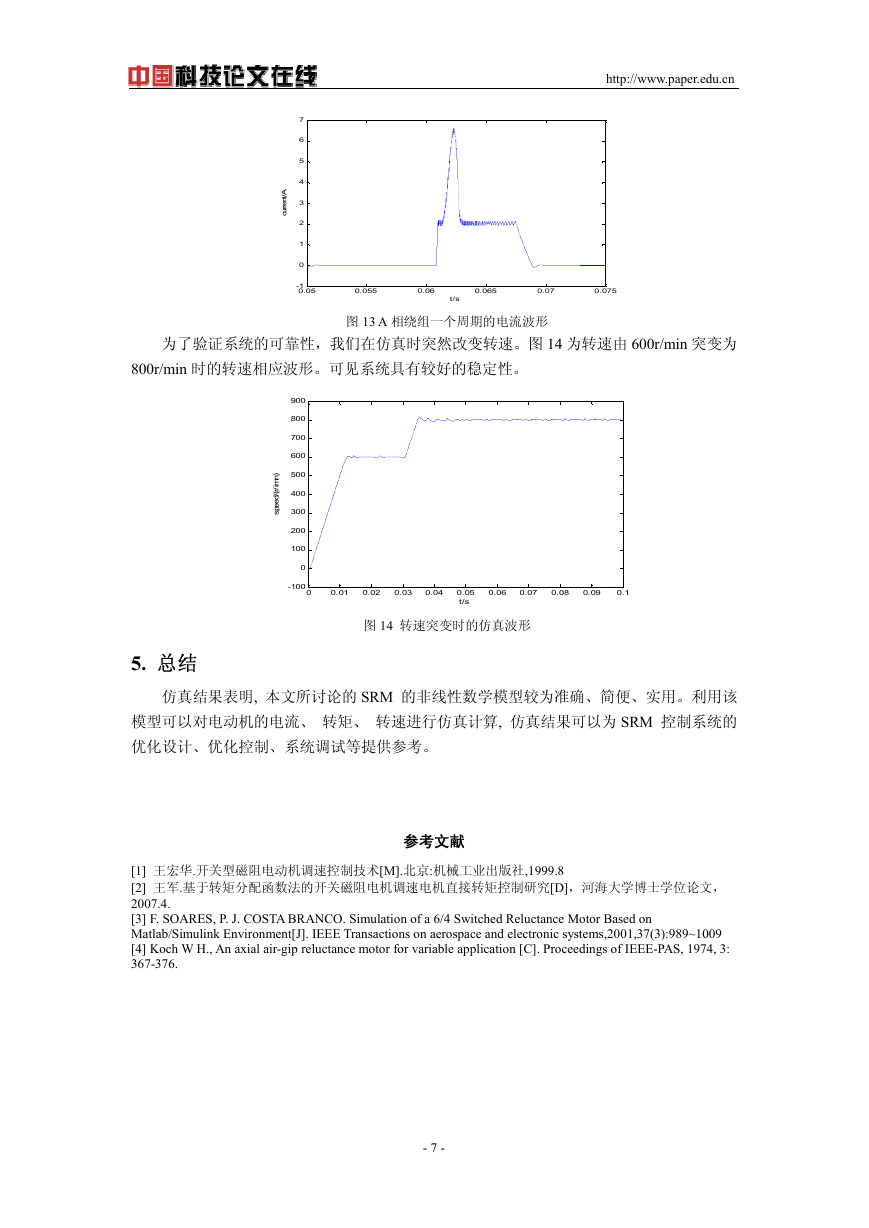
http://www.paper.edu.cn 7 6 5 4 3 2 1 0 / A nt e r ur c -1 0.05 0.055 0.06 0.065 0.07 0.075 t/s 图 13 A 相绕组一个周期的电流波形为了验证系统的可靠性，我们在仿真时突然改变转速。图 14 为转速由 600r/min 突变为 800r/min 时的转速相应波形。可见系统具有较好的稳定性。 900 800 700 600 500 400 300 200 100 0 ) n m i / r ( d/ e e p s -100 0 0.01 0.02 0.03 0.04 0.05 t/s 0.06 0.07 0.08 0.09 0.1 图 14 转速突变时的仿真波形 5. 总结仿真结果表明, 本文所讨论的 SRM 的非线性数学模型较为准确、简便、实用。利用该模型可以对电动机的电流、转矩、转速进行仿真计算, 仿真结果可以为 SRM 控制系统的优化设计、优化控制、系统调试等提供参考。参考文献 [1] 王宏华.开关型磁阻电动机调速控制技术[M].北京:机械工业出版社,1999.8 [2] 王军.基于转矩分配函数法的开关磁阻电机调速电机直接转矩控制研究[D]，河海大学博士学位论文， 2007.4. [3] F. SOARES, P. J. COSTA BRANCO. Simulation of a 6/4 Switched Reluctance Motor Based on Matlab/Simulink Environment[J]. IEEE Transactions on aerospace and electronic systems,2001,37(3):989~1009 [4] Koch W H., An axial air-gip reluctance motor for variable application [C]. Proceedings of IEEE-PAS, 1974, 3: 367-376. - 7 -

http://www.paper.edu.cn Nonlinear Modeling and Simulation of Switched Reluctance Motor Drive Using Matlab Institute of Electrical Engineering, Hohai University, Nanjing (210098) Yan Rongchao Abstract Switched Reluctance Drive(SRD),which is made from SR motor, has a large start torque, a wide scope of velocity modulation and a high efficiency. Modeling and simulation for a 6/4 SRM will be presented in this paper by using Matlab/SimPowerSystems based on its basic principles and mathematical theory. In Simulink, the independent functional blocks, such as Motor model block, Speed controller block, Current controller block, Angle selection block, ect., have been modeled. By the organic combination of these blocks, the model of control system can be established easily. In the double loop of control system, a PI controller is adopted in the speed loop and a compound current controller is adopted in the current loop. In order to obtain expected performance, above base speed a speed angular position controller works in current closed-loop, and below base speed a current chopping controller works. The reasonability and validity have been testified by the simulation results. Keywords : Switched Reluctance Motor (SRM); MATLAB; dynamic model - 8 -

资料库

开关磁阻电机的MATLAB仿真建模研究.pdf

相关推荐

开发技术

热门标签

最新资料