logo资料库

MATLAB在求二阶系统中阶跃响应的分析及应用.doc

发布时间：2022-06-08 发布人：admin 分类：说明书 资料大小：0.55M 资料格式：doc 举报 版权申诉
第1页 / 共9页
第2页 / 共9页
第3页 / 共9页
第4页 / 共9页
第5页 / 共9页
第6页 / 共9页
第7页 / 共9页
第8页 / 共9页
资料共9页，剩余部分请下载后查看
    摘要
    1 训练目的和要求
    2 理论分析计算
    已知系统的传递函数为，求其阶跃响应。并分析
    本题要求求解一个简单的二阶系统的传递函数的阶跃响应，研究二阶系统的特征参数，当无阻尼自然频率
    3 MATLAB仿真
    3.1 程序一（用函数来求解）
    3.2 程序二（使用内置函数step）
    4 Simulink仿真
    4.1 Simulink简介
    4.2 仿真过程
    5 小结
    参考文献
    武汉理工大学《基础技能强化训练》课程设计说明书 摘要 二阶系统控制系统按数学模型分类时的一种形式，是用数学模型可表示为二阶线 性常微分方程的系统。 二阶系统的解的形式，可由对应传递函数 W(s) 的分母多项 式 P(s)来判别和划分，P(s) 的一般形式为变换算子 s 的二次三项代数式。 代数方程 P(s)=0 的根 ，可能出现四种情况。 1.两个实根的情况，对应于两个串联的一阶系统。如果两个根都是负值，就 为非周期性收敛的稳定情况。 2.当 a1 ＝0，a2>0 ，即一对共轭虚根的情况,将引起频率固定的等幅振荡，是 系统不稳定的一种表现。 3.当 a1<0 ，a1-4a2<0 ，即共轭复根有正实部的情况，对应于系统中发生发 散型的振荡,也是不稳定的一种表现。 4.当 a1>0 ，a1-4a2<0 ，即共轭复根有负实部的情况，对应于收敛型振荡， 且实部和虚部的数值比例对输出过程有很大的影响。一般以阻尼系数ζ来表征，取 在 0.4~0.8 之间为宜 。当ζ>0.8 后，振荡的作用就不显著，输出的速度也比较 慢。而ζ<0.4 时，输出量就带有明显的振荡和较大的超调量，衰减也较慢 ，这也 是控制系统中所不希望的。 当激励为单位阶跃函数时，电路的零状态响应称为单位阶跃响应，简称阶跃 响应。阶跃响应 g(t) 定义为：系 统在单位阶跃信号 u(t) 的激励下产生的零状态 响应。 关键词：二阶系统 阶跃响应 MATLAB/Simu link 1
    武汉理工大学《基础技能强化训练》课程设计说明书 MATLAB 在求二阶系统中阶跃响应的分析 及应用 1 训练目的和要求 通过对 MATLAB 仿真软件的语言的学习，学会在 MATLAB 中解决《电路原 理》、《模拟电子技术基础》、《数字电子技术基础》等所学课本上的问题，进一 步熟悉并掌握 MATLAB 在电路、信号与系统、自动控制原理、数字信号处理等中的应 用。 通过对软件的应用，巩固已学知识。以求达到通过训练能熟练掌握 MATLAB 的应 用，能够深入到实际问题中。 要求通过理论分析所要求题目并通过 MATLAB 仿真比较实验结果。 2 理论分析计算 已知系统的传递函数为 1 2 s 2 s 1  ，求其阶跃响应。并分析变化时，其阶跃响应的 变化情况。 本题要求求解一个简单的二阶系统的传递函数的阶跃响应，研究二阶系统的特 征参数，当无阻尼自然频率 n 为 1 时阻尼比 对系统动态性能的影响。 了解一下基础知识后就可以很自然的解决题目了，我们可以对二阶系统的传 递函数进行分析后对无阻尼自然频率赋值 1 来求解。然后再用 MA TLAB 仿真。 二阶系统传递函数标准形式： ( ) G s  1 2 Ts    1 2 2 T s  2  s 2 2  n 2   n  s n 2
    武汉理工大学《基础技能强化训练》课程设计说明书 其中，T—为时间常数，也称为无阻尼自由振荡周期 n —自然频率（或无阻尼振荡周期） ζ －阻尼比（相对阻尼系数） 二阶系统的特征方程： 2 S  2  n nS  2  0 特征根为： S 2,1   n  n 12  由题目可知， n =1，ζ为一参数，因此对于ζ的取值进行分类说明 (1)欠阻尼 0 < ζ < 1 S 2,1  2 1    j n n )( sC   )( )( sRs  2 S   1 S  ( S  S   n  n )  2  2  d 2 n  n 2 S   n  n 2 )  n  S (  2 1 S  2  d 1)( th  e tn   1   1  1 2  e t   d [cos  2       ) sin( 1  t nt d sin  d t ] t  0 将 n =1 带入，可得到阻尼比在此区间内时的阶跃响应。 3
    武汉理工大学《基础技能强化训练》课程设计说明书 （2）临界阻尼ζ = 1 )( sC  2  n   n 2 )  1 S  1 S ( S  ( S  n   n  S 2 ) 1   n 临界阻尼情况下的二阶系统的单位阶跃响应称为临界阻尼响应 t  n c(t) 1 e     n 将 n =1 带入，可得到阻尼比在此区间内时的阶跃响应。 1 e     (1  n  n e t n t t t) t 0  特点：单调上升，无振荡，无超调，趋近于 1，无稳态误差。 (3)过阻尼 ζ > 1 S 2,1  2    1 n n )( sC   n )( S 1 ( S  2 S  S ) 2  1 S  [ S  2  n )][1 S   2   ( n 2   ( n  )]1 S A 2  2  ( n   )1  A 1 S  S  1 A 1 A 3  2   (  )1 n A 2  A 3   1   1 2   )1  )1 S  2 n ( 2 2   (1 c(t) 1   2 1 2 1)      1( 2 2 ( 1) t      e n  4 2 1 2 1)      1( 2 2 ( 1) t      e n t 0 
    武汉理工大学《基础技能强化训练》课程设计说明书 将 n =1 带入，可得到阻尼比在此区间内时的阶跃响应。 特点：单调上升，无振荡，过度过程时间长，趋近于 1，无稳态误差。 （4）无阻尼状态 ζ = 0 s 1,2 jw  n 系统有一对共轭虚根 系统在无阻尼下的单位阶跃响应为： c(t) 1 cos w t n   (t  0) 结论：二阶系统的阻尼比ξ决定了其振荡特性 ζ< 0 时，阶跃响应发散，系统不稳定； ζ≥ 1 时，无振荡、无超调，过渡过程长； 0<ζ<1 时，有振荡，ξ愈小，振荡愈严重,但响应愈快； ζ= 0 时，出现等幅振荡。 3 MATLAB 仿真 根据以上理论分析，用 MATLAB 编程分析。可以用两种方法求解。 3.1 程序一（用函数来求解） 由传递函数与阶跃响应的关系，编程如下： )( sC   )( )( sRs  2 S  2  n 5 2  n  S n  2 1 S
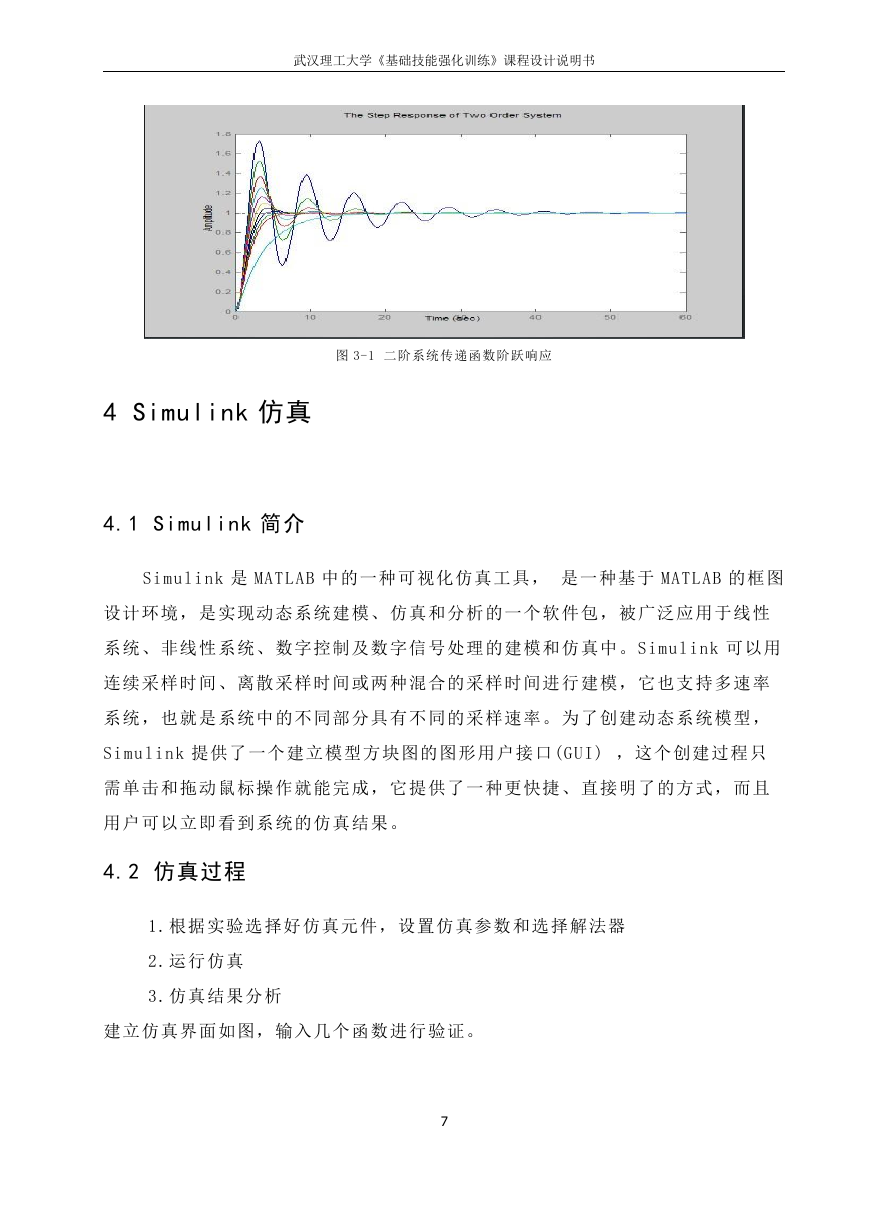
    武汉理工大学《基础技能强化训练》课程设计说明书 syms s syms x %定义系统参数s %定义阻尼比x ilaplace( (1/(s^3 + 2*x*s^2 + s ))) %拉普拉斯逆变换函数求解 ans = 1-(cosh(t*(x^2-1)^(1/2)) + (x*sinh(t*(x^2-1)^(1/2)))/(x^2-1)^(1/2))/exp(t*x) %带有阻尼比参数的阶跃响应 3.2 程序二（使用内置函数 step） ko sai=[0.1:0 .1:1.0,2. 0]; fi gure(1) ho ld on fo r i=kosai nu m=1; de n=[1,2*i,1 ]; st ep(num,den ) en d ti tle('The St ep Response of Two Order Syst em'); ho ld off 结果如图 3-1 所示： 6
    武汉理工大学《基础技能强化训练》课程设计说明书 图 3-1 二阶系统传递函数阶跃响应 4 Simulink 仿真 4.1 Simulink 简介 Si mulink 是 MAT LAB 中的一种可视化仿真工具， 是一种基于 MATLAB 的框图 设计环境，是实现动态系统建模、仿真和分析的一个软件包，被广泛应用于线性 系统、非线性系统、数字控制及数字信号处理的建模和仿真中。Simulink 可以用 连续采样时间、离散采样时间或两种混合的采样时间进行建模，它也支持多速率 系统，也就是系统中的不同部分具有不同的采样速率。为了创建动态系统模型， Si mulink 提供了一个建立模型方块图的图形用户接口(GUI) ，这个创建过程只 需单击和拖动鼠标操作就能完成，它提供了一种更快捷、直接明了的方式，而且 用户可以立即看到系统的仿真结果。 4.2 仿真过程 1. 根据实验选择好仿真元件，设置仿真参数和选择解法器 2. 运行仿真 3. 仿真结果分析 建立仿真界面如图，输入几个函数进行验证。 7
    武汉理工大学《基础技能强化训练》课程设计说明书 图 4-1ζ=0.1 时仿真图 图 4-2 ζ=0.1 时仿真结果 对ζ取不同值进行验证，结果如下： 图 4-3ζ=0.3 时仿真结果 图 4-4ζ=1 时仿真结果 图 4-5 ζ=0.1 时仿真结果 分析比较可知以上几种方法结果一样。 5 小结 通过本次强化训练，我基本了解并掌握了 MATLAB 在电路原理中的应用，知道了 如何在 MATLAB 以及 simulink 里面处理分析电路方面的问题，对待电子方面知识学 习我又了解了一个强有力的仿真工具，对以后也会有很大的帮助。 通过本次实验了解到，MATLAB 是矩阵实验室（Matrix Laboratory）的简称， 是美国 MathWorks 公司出品的商业数学软件，用于算法开发、数据可视化、数据分 析以及数值计算的高级技术计算语言和交互式环境，主要包括 MATLAB 和 Simulink 两大部分。MATLA B 的基本数据单位是矩阵，它的指令表达式与数学、工程中常用 的形式十分相似，故用 MATLA B 来解算问题要比用 C， FORT RAN 等语言完成相同的 事情简捷得多，并且 ma thwork 也吸收了像 Maple 等软件的优点,使 MATLA B 成为 一个强大的数学软件。在新的版本中也加入了对 C，FORTRAN ，C+ + ，JAVA 的支 持。可以直接调用,用户也可以将自己编写的实用程序导入到 MATLA B 函数库中方 便自己以后调用。应用到自动控制方面也很方便。 通过 MA TLAB 在电路原理二阶系统求阶跃响应的分析实验过程中，不仅了解 到了 MATLAB 强大的功能，而且分析起来非常方便，各种参数调整起来很简洁， 生成图像后分析结果一目了然。可以非常直观的比较分析随阻尼比参数变化节约 8
    分享到：
    赞 收藏

    相关推荐

    资料库

    课程资源

    共收录17145份资料，累计13个分类，关注成员有19位，主要包括：PHP,网络管理,网页制作,Java,.Net,数据库,3G/移动开发,C/C++,游戏开发,嵌入式,讲义,软件测试,专业指导

    热门标签

    PHP 网络管理 网页制作 Java .Net 数据库 3G/移动开发 C/C++ 游戏开发 嵌入式 讲义 软件测试 专业指导

    最新资料