详解快速傅里叶变换FFT算法.pdf-资料库

a13a0211-5841-4f5e-bc41-b308f3d855d3.pdf-第1页.png

第1页 / 共17页

a13a0211-5841-4f5e-bc41-b308f3d855d3.pdf-第2页.png

第2页 / 共17页

a13a0211-5841-4f5e-bc41-b308f3d855d3.pdf-第3页.png

第3页 / 共17页

a13a0211-5841-4f5e-bc41-b308f3d855d3.pdf-第4页.png

第4页 / 共17页

a13a0211-5841-4f5e-bc41-b308f3d855d3.pdf-第5页.png

第5页 / 共17页

a13a0211-5841-4f5e-bc41-b308f3d855d3.pdf-第6页.png

第6页 / 共17页

a13a0211-5841-4f5e-bc41-b308f3d855d3.pdf-第7页.png

第7页 / 共17页

a13a0211-5841-4f5e-bc41-b308f3d855d3.pdf-第8页.png

第8页 / 共17页

详解快速傅里叶变换 FFT 算法快速傅里叶变换 FFT 是离散傅里叶变换 DFT 的一种快速算法，只有 FFT 才能在现实中有实际应用的意义。虽然许多学过数字信号处理这门课的同学都知道 DFT 和 FFT，但实际上真正理解其算法原理的屈指可数，绝大部分同学知其然而不知其所以然，况且限于高校课程教学体制，课堂上不可能把这些原理和算法讲得明明白白的。为此，特意以本文讲解 FFT 算法的原理与实际应用，给欲往电子信息类专业进修和发展的同学一些课外参考。 N 点有限长序列 x(n)的 DFT 为其中其逆变换 IDFT 为正逆变换的运算量都是相同的。x(n)和 X（k）都是复数序列，计算一个 X(k)值，需要 N 次复数乘法和 N-1 次复数加法。X(k)有 N 个点，所以总共需要 N*N 次复数乘法和 N(N-1)次复数加法。复数运算实际上是通过实数运算来完成的。上式可以写成：由此可见，一次复数乘法需要 4 次实数乘法和 2 次实数加减法。一次复数加法需要 2 次实数加法。所以每一个 X（k）计算需要 4N 次实数乘法以及 2N+2(N-1)=2(2N-1)次实数加法。整个 DFT 运算总共需要 4N*N 次实数乘法和 N*2(2N-1)=2N(2N-1)次实数加法。当 N 足够大，N>>1 时，直接计算 DFT 的乘法次数和加法次数都是和 N 的平方成正比。当 N=1024 时，DFT 的运算量为 1048576 次，即一百多万次复乘运算，一块嵌入式 32 位处理器的最高速度为 105 百万指令每秒，那么它要完全计算这个 DFT 的时间最快也要 1 秒，期间还是独占 CPU 所有运算资源且不能有任何其他的中断请求。这样计算量太庞大，计算速递太慢了，谈不上实时性，根本没有实用意义。所以，我们就要利用 DFT 的系数的固有特性来简化计算，减少运算量。特性如下： 1. 共轭对称性： 2. 周期性： 3. 可约性：得出：利用上述这些系数性质就可以合并 DFT 某些项的计算从而减少计算量。下面仅给出按时间抽选 10()()WNnkNnXkxn2jnknkNNWe101x(n)X(k)WNnkNnN10()Re()Im()ReImNnknkNNnXkxnjxnWjW10Re()ReIm()ImRe()ImIm()ReNnknknknkNNNNnxnWxnWjxnWxnW()*nknkNNWW()()nknNknkNNNNWWW//nknmknkmNNNmWWW()()nNkNnknkNNNWWW/21NNW(/2)kNkNNWW

DIT 的基-2 FFT 算法，也就是库利-图基算法的思路，其详细推导过程教科书上讲得更明白。设点数 N=2^m，N=8，16，32，64„„1024，2048 先将 x(n)序列按 n 的奇偶性分成奇偶两组，每组的点数为 N/2-1。偶：x(2r)=x1(r) 奇：x(2r+1)=x2(r) 则有利用系数 W 的可约性：上式可以表示为一个 N 点 DFT 分解成两个 N/2 点的 DFT，此时 X(k)只计算了前 N/2 个，而后 N/2 个的计算需要应用系数的周期性 ,根据欧拉公式推导即得：于是得出前半部分和后半部分分别为：只需求 0~N/2-1 部分的 X1 和 X2，即可求出 0~N-1 的所有 X(k)。根据这两个式子，可以画出蝶形信号流图： X1(k) 1 X2(k) -1 每个蝶形运算需要一次复数乘法和两次复数加减法。当分解成两个 N/2 点 DFT 的蝶形运算后，一个 N/2 点需要(N/2)^2=N^2/4 次复数乘法和 N/2(N/2-1)次复数加法。两个 N/2 点 DFT 需要 2(N/2)^2=N^2/2 次复数乘法和 N(N/2-1)次复数加法。把两个 N/2 点 DFT 合成 N 点 DFT 有 N/2 个蝶形运算，则还需要 N/2 个复数乘法和 N 个复数加法。总共需要 N^2/2+N/2=N(N+1)/2，约等于 N^2/2 次复数乘法，N(N/2-1)+N=N^2/2 次复数加法。对比前面所说的直接 DFT 的运算量便知此次减少了多少运算量。 1/21/212212000()()W(r)(W)W(r)(W)rkrkNNNnkkNNNNnrrXkxnxx2222/2/2jjNNNNWeeW/21/211/22/21200()(r)WW(r)W()W()NNrkkrkkNNNNrrXkxxXkXk(/2)/2/2rkrkNNNWW11()(k)2NXkX22()(k)2NXkX22NNkkkNNNNWWWW12()(k)W(k)kNXkXX12()(k)W(k)2kNNXkXX12(k)W(k)kNXXkNW12(k)W(k)kNXX

再将 N/2 分解为两个 N/4 点 DFT，那么 8 点 DFT 则可分解成四个 N/4=2 点 DFT。利用四个 N/4 点的 DFT 及两级蝶形组合运算来计算 N 点 DFT，比只用一次分解的组合方式的计算量又减少了一半。 DFT 的运算量集中在 N 点 DFT 计算部分，尽力把多点直接 DFT 分解成少点直接 DFT，尽量减少直接 DFT 的点数，就可以压低整个 DFT 的运算量。

在把原序列多次逐级分解为奇偶两组的过程中，其序列标号是如何变化的呢？观察下面便知： (100)(101)(110)(111) 原序列：x0, x1, x2, x3, x4, x5, x6, x7, (000)(001)(010)(011) 因此可得：偶:x0(000),x4(100) 偶原序列奇:x2(010),x6(110) 偶:x1(001),x5(101) 奇奇:x3(011),x7(111) 3(0)X3(1)X4(0)X4(1)X5(0)X5(1)X6(0)X6(1)X1(0)X1(1)X1(2)X1(3)X2(0)X2(1)X2(2)X2(3)X3(0)x3(1)x4(0)x4(1)x5(0)x5(1)x6(0)x6(1)x

上图中无下标的 x(n)和 X(k)分别代表原序列和转换后的序列。有下标的 x(n)和 X(k)分别指的是原序列的分组和转换后的分组，下标相同代表同属一组，括号里的序号为点数。A(0)-A(7)是指内存中的储存单元。把原序列 x(0),x(1)„„x(7)按奇偶分组后得到 x3(n),x4(n),x5(n),x6(n)四组，则每组有 N/4=2 点，即其中的 n=0,1。用前面分解 N/2 点的方法再分解一次便得：把上面四式具体化表示，仅列出 X4(k)作为例子：只有两点 k=0,1 上式中，故上式不需要乘法，只有加减。同样按这个方法可以求出其他分组，而且这些两点 DFT 都可用一个蝶形结表示。下图是直接 DFT 与 FFT 算法的运算量的差距：蝶形运算的一般规律：原位运算细心观察 8 点 DIF-FFT 运算流程图可以归纳出蝶形运算的一般规律，其每级每列计算都是由 N/2 个蝶形运算构成，每一个蝶形运算如下式所示： 1433/40(k)()NlkNlXxlW1444/40(k)()NlkNlXxlW1455/40(k)()NlkNlXxlW1466/40(k)()NlkNlXxlW11444/44/400(k)()NlklkNNllXxlWxW00044242(0)(0)(1)(2)(6)(2)(6)NXxWxxWxxWx11044242(1)(0)(1)(2)(6)(2)(6)NXxWxxWxxWx2110221jjNWeeW

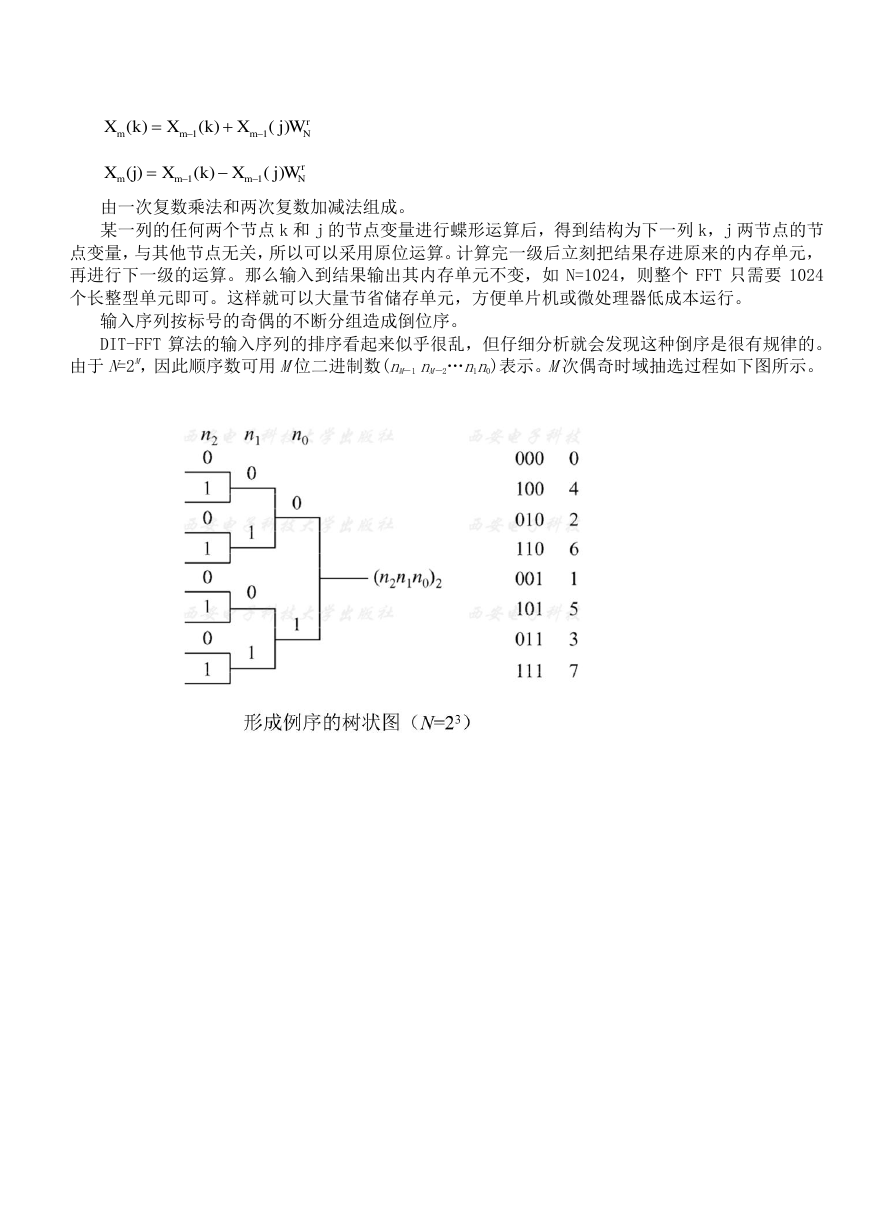
由一次复数乘法和两次复数加减法组成。某一列的任何两个节点 k 和 j 的节点变量进行蝶形运算后，得到结构为下一列 k，j 两节点的节点变量，与其他节点无关，所以可以采用原位运算。计算完一级后立刻把结果存进原来的内存单元，再进行下一级的运算。那么输入到结果输出其内存单元不变，如 N=1024，则整个 FFT 只需要 1024 个长整型单元即可。这样就可以大量节省储存单元，方便单片机或微处理器低成本运行。输入序列按标号的奇偶的不断分组造成倒位序。 DIT-FFT 算法的输入序列的排序看起来似乎很乱，但仔细分析就会发现这种倒序是很有规律的。由于 N=2M，因此顺序数可用 M位二进制数(nM－1 nM－2„n1n0)表示。M次偶奇时域抽选过程如下图所示。 11()()()rmmmNXkXkXjW11(j)()()rmmmNXXkXjW

细心观察 8 点 DIF-FFT 运算流程图还可以看出每蝶形的两个节点距离为 2^(m-1)。一级，两节点为 1 二级，两节点为 2 三级，两节点为 4 根据上述规律可将蝶形运算的一般等式写成通式：（m 是第 m 级运算）求旋转因子 W 中 r 的算法：将上式中 k 换成 L 位二进制数（N=2^L），再乘以 2^(L-m)，即将 L 位二进制数左移 L-m 位，右边补零，即可求出 r。所以最终所需要的储存单元有 N 个+旋转因子 W 的 N/2 个=N+N/2 个储存单元。要说明的是，按时域抽取法 DIT 与按频域抽取法 DIF 的基本蝶形是互为转置的，所以两种方法的本质是一样的，只是表现形式不同而已。转置就是将流图的所有支路方向都反相，并且交换输入与输出，但节点变量值不交换。在此就不详说 DIF 法了。再说明一下离散傅里叶逆变换 IDFT 的算法 IFFT。只要对 IDFT 公式取共轭：得到：此式表明只要先将 X(k)取共轭，就可以直接利用 FFT 子程序，最后再将运算结果取一次共轭，并乘以 1/N 即得到 x(n)值，因此 FFT 和 IFFT 可以共用一个程序。 11()()()rmmmNXkXkXjW111()()(k2)mrmmmNXkXkXW11(j)()()rmmmNXXkXjW1111(2)()(k2)mmrmmmNXkXkXW101()IDFT()(k)WNnkNkxnXkXN1**01()(k)WNnkNkxnXN*1***011()(k)W()NnkNkxnXDFTXkNN

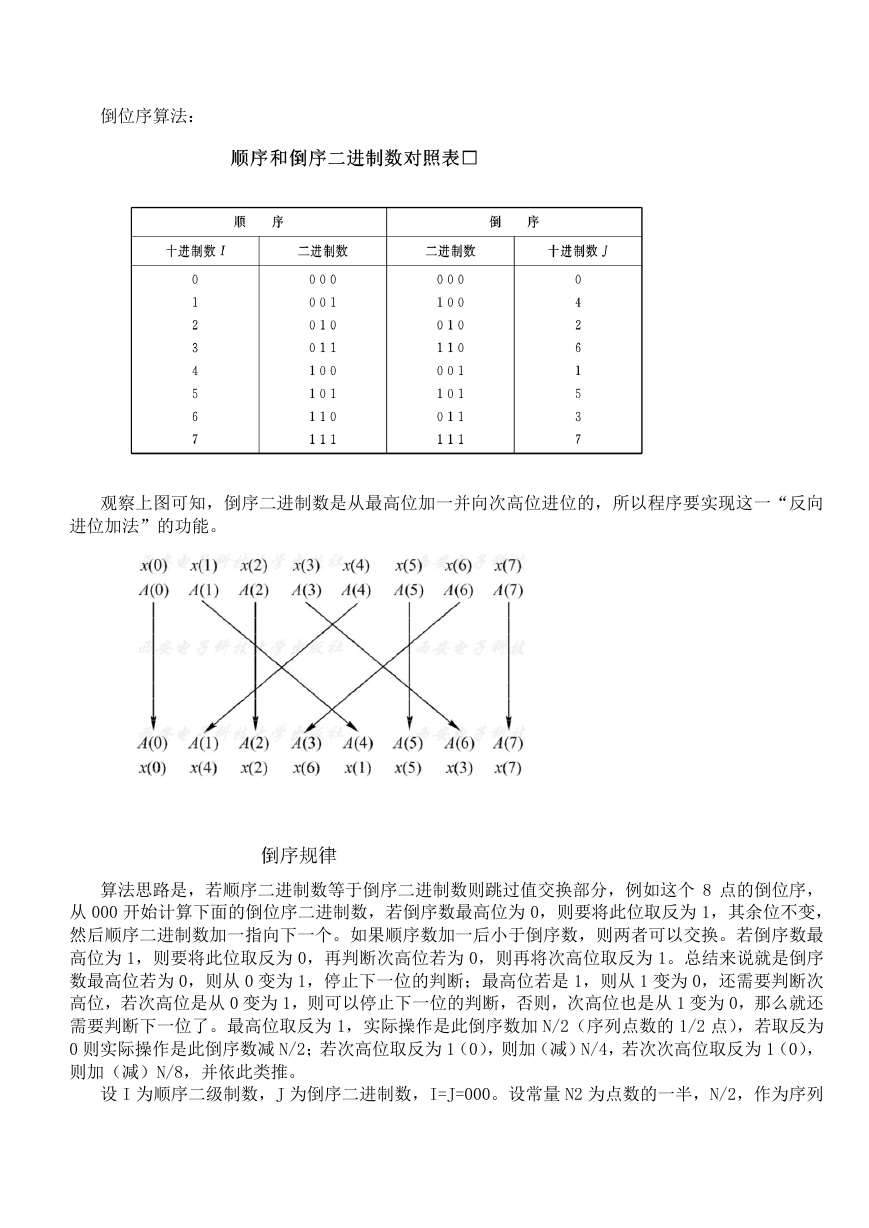
倒位序算法：观察上图可知，倒序二进制数是从最高位加一并向次高位进位的，所以程序要实现这一“反向进位加法”的功能。算法思路是，若顺序二进制数等于倒序二进制数则跳过值交换部分，例如这个 8 点的倒位序，从 000 开始计算下面的倒位序二进制数，若倒序数最高位为 0，则要将此位取反为 1，其余位不变，然后顺序二进制数加一指向下一个。如果顺序数加一后小于倒序数，则两者可以交换。若倒序数最高位为 1，则要将此位取反为 0，再判断次高位若为 0，则再将次高位取反为 1。总结来说就是倒序数最高位若为 0，则从 0 变为 1，停止下一位的判断；最高位若是 1，则从 1 变为 0，还需要判断次高位，若次高位是从 0 变为 1，则可以停止下一位的判断，否则，次高位也是从 1 变为 0，那么就还需要判断下一位了。最高位取反为 1，实际操作是此倒序数加 N/2（序列点数的 1/2 点），若取反为 0 则实际操作是此倒序数减 N/2；若次高位取反为 1（0），则加（减）N/4，若次次高位取反为 1（0），则加（减）N/8，并依此类推。设 I 为顺序二级制数，J 为倒序二进制数，I=J=000。设常量 N2 为点数的一半，N/2，作为序列

资料库

详解快速傅里叶变换FFT算法.pdf

相关推荐

后端

热门标签

最新资料