Kaggle Titanic项目报告；数据挖掘期末作业；.doc

发布时间：2022-05-31 发布人：admin 分类：说明书资料大小：1.84M 资料格式：doc 举报版权申诉

zhihuichen-12658371-16359647989167321257.doc.pdf-第1页.png

第1页 / 共15页

zhihuichen-12658371-16359647989167321257.doc.pdf-第2页.png

第2页 / 共15页

zhihuichen-12658371-16359647989167321257.doc.pdf-第3页.png

第3页 / 共15页

zhihuichen-12658371-16359647989167321257.doc.pdf-第4页.png

第4页 / 共15页

zhihuichen-12658371-16359647989167321257.doc.pdf-第5页.png

第5页 / 共15页

zhihuichen-12658371-16359647989167321257.doc.pdf-第6页.png

第6页 / 共15页

zhihuichen-12658371-16359647989167321257.doc.pdf-第7页.png

第7页 / 共15页

zhihuichen-12658371-16359647989167321257.doc.pdf-第8页.png

第8页 / 共15页

1 项目介绍

1.1比赛任务

1.2数据

1.3问题归类

2 项目知识点

2.1 数据分析

2.1.1 数据整体情况

2.1.2 数值类型数据分布

2.1.3 离散类型数据分布

2.2 各字段与survived之间的关联性

2.2.1 离散型特征与survived之间的关联性

2.2.2 连续型特征与survived之间的关联性

2.3 特征处理

2.4 模型的选择

3 实验过程

(1)读取数据和合并训练集和测试集

(2)特征处理：对缺失数据填充、特征值的转换以及数据分组等处理（具体代码在2.3节已给出）

(3)模型数据准备

(4)模型训练比较：测试各个模型得分情况，选择得分最高的随机森林。

(5)各特征的重要性

(6)模型调参

(7)结果预测

(8)提交预测结果

4 项目结果

5 项目总结

教师评语：项目名称： Titanic:Machine Learning from Disaster 摘要：Titanic 项目主要的任务是根据乘客的信息预测是否生存。首先大致了解数据的整体情况和分布情况，缺失数据严不严重。分析各个属性与 survived 标签的关联性，依次进行特征处理，如对缺失数据填充、特征值的转换以及数据分组等处理。比较 Logistic Regression、Support Vector Machines、KNN、 Naive Bayes、Linear SVC、Stochastic Gradient Decent、Decision Tree 和 Random Forest 模型得分情况，选定 Random Forest 模型。最后，模型调参得到预测结果。该项目最终的比赛成绩是准确率达到 0.8，还有一定的改进空间。

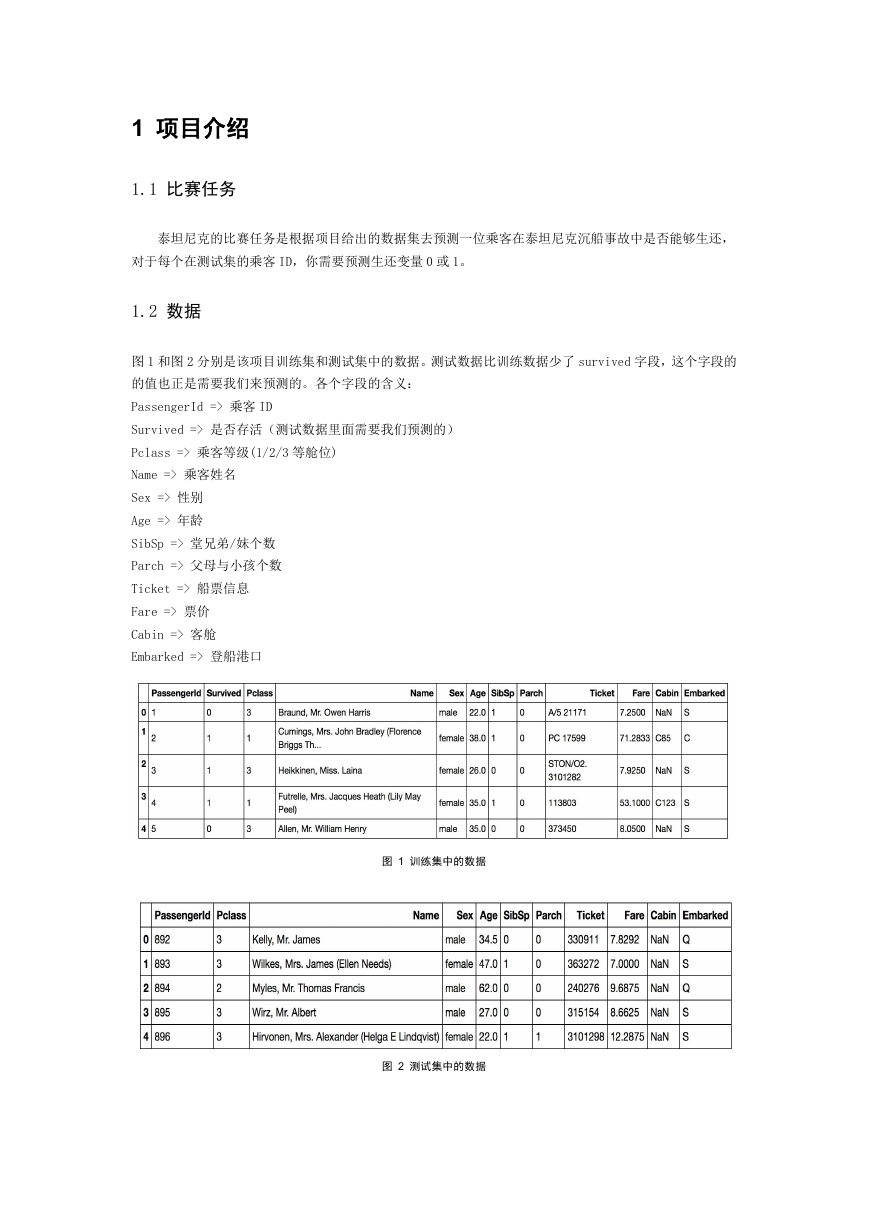
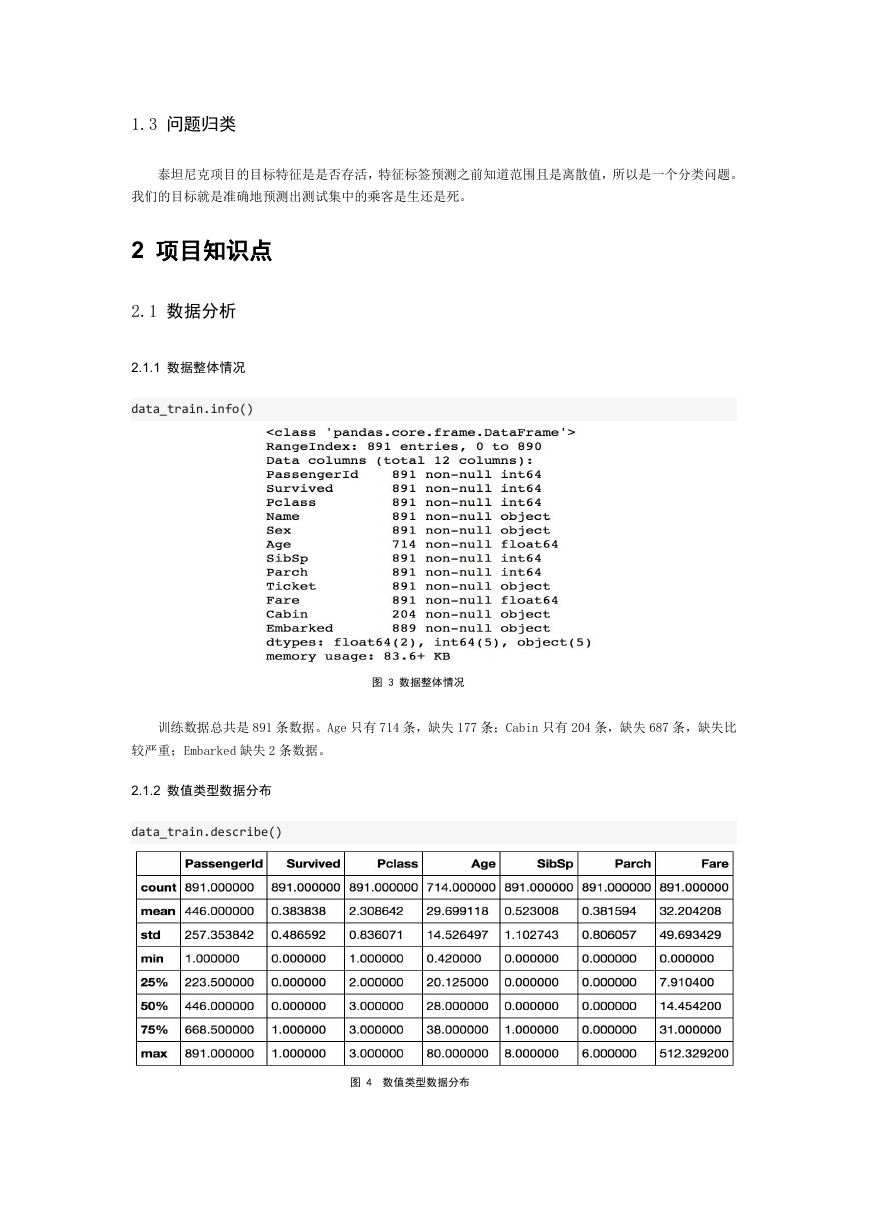
1 项目介绍 1.1 比赛任务泰坦尼克的比赛任务是根据项目给出的数据集去预测一位乘客在泰坦尼克沉船事故中是否能够生还，对于每个在测试集的乘客 ID，你需要预测生还变量 0 或 1。 1.2 数据图 1 和图 2 分别是该项目训练集和测试集中的数据。测试数据比训练数据少了 survived 字段，这个字段的的值也正是需要我们来预测的。各个字段的含义： PassengerId => 乘客 ID Survived => 是否存活（测试数据里面需要我们预测的） Pclass => 乘客等级(1/2/3 等舱位) Name => 乘客姓名 Sex => 性别 Age => 年龄 SibSp => 堂兄弟/妹个数 Parch => 父母与小孩个数 Ticket => 船票信息 Fare => 票价 Cabin => 客舱 Embarked => 登船港口图 1 训练集中的数据图 2 测试集中的数据

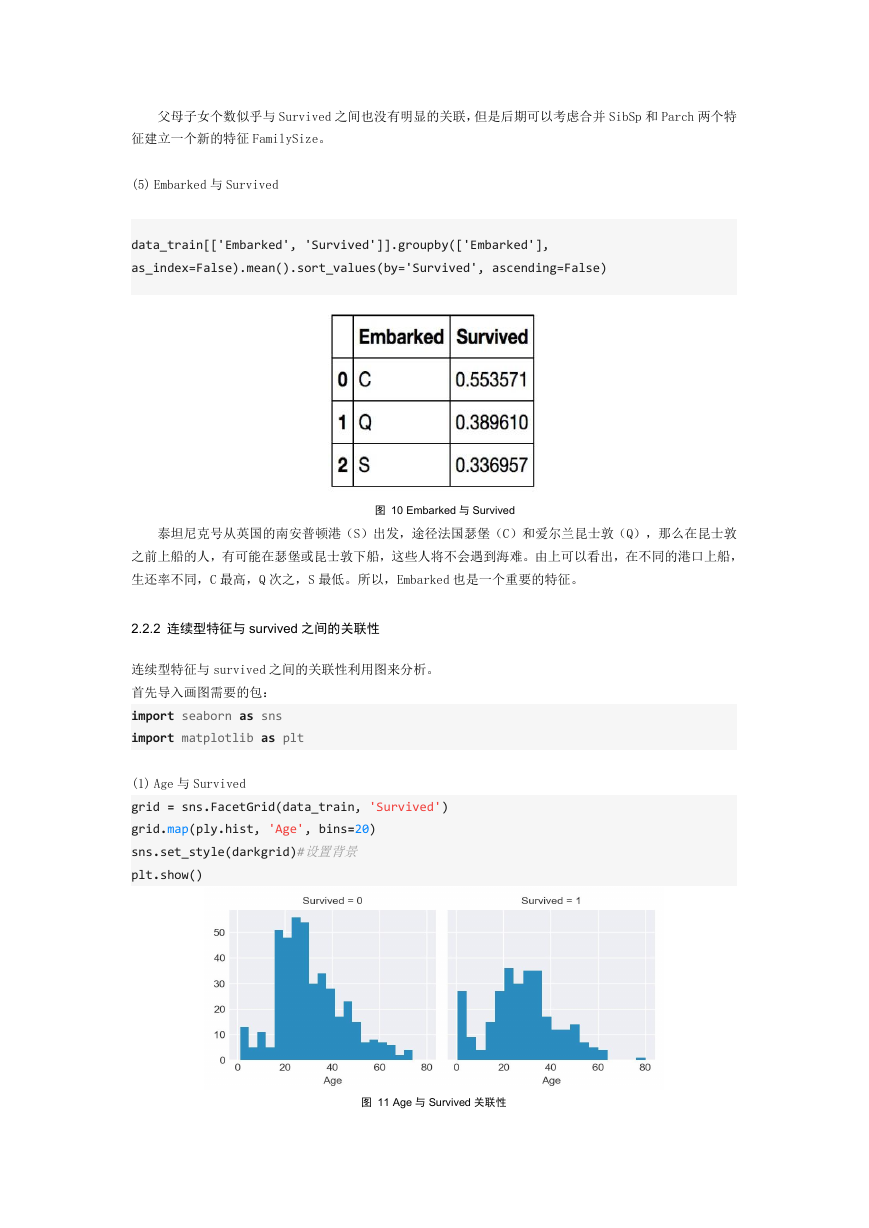
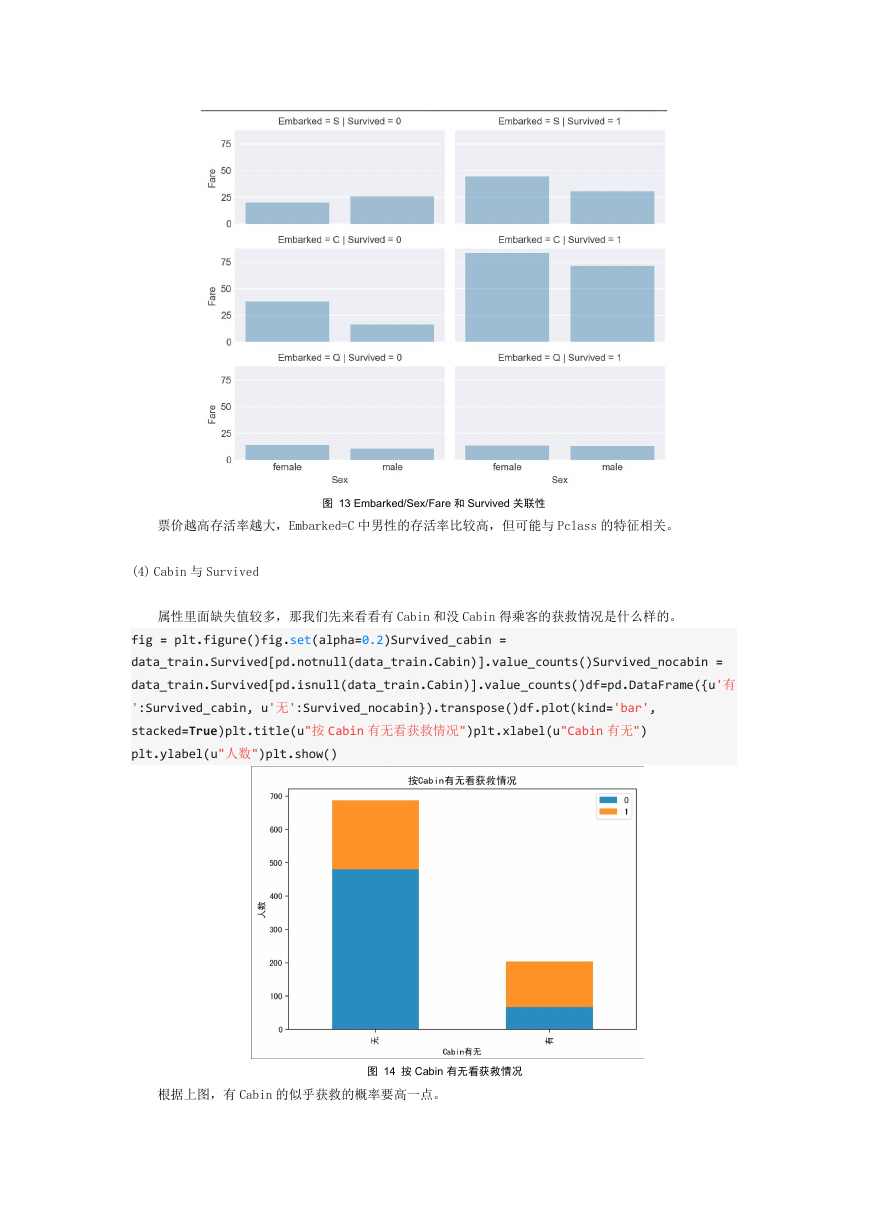
1.3 问题归类泰坦尼克项目的目标特征是是否存活，特征标签预测之前知道范围且是离散值，所以是一个分类问题。我们的目标就是准确地预测出测试集中的乘客是生还是死。 2 项目知识点 2.1 数据分析 2.1.1 数据整体情况 data_train.info() 图 3 数据整体情况训练数据总共是 891 条数据。Age 只有 714 条，缺失 177 条；Cabin 只有 204 条，缺失 687 条，缺失比较严重；Embarked 缺失 2 条数据。 2.1.2 数值类型数据分布 data_train.describe() 图 4 数值类型数据分布

根据图 4 的结果可知，在训练数据中，大概 38%的人最后获救。Pclass 中 2、3 船舱的人要比 1 多。大部分人的年龄在 38 岁以内，最大的年龄是 80。大多数乘客没有携带家属。票价差异比较大，只有 1%不到的乘客购买了 512$的船票。 2.1.3 离散类型数据分布 data_train.describe(include=[np.object]) 图 5 离散类型数据分布根据图 5 的结果可知，Name 属性是唯一，没有重名；性别就男和女；Ticket 不是唯一的，891 名乘客只有 681 张船票，说明可能有的是和亲人共用一张船票的；登录港口是 3 个。 2.2 各字段与 survived 之间的关联性 2.2.1 离散型特征与 survived 之间的关联性 (1)Pclass 与 Survived data_train[['Pclass', 'Survived']].groupby(['Pclass'], as_index=False).mean().sort_values(by='Survived', ascending=False) Pclass 的数值越小最后获救的概率越大，并且很明显，后期可做为一个建模特征。图 6 Pclass 与 Survived 关联性 (2) Sex 与 Survived data_train[['Sex', 'Survived']].groupby(['Sex'], as_index=False).mean().sort_values(by='Survived', ascending=False)

Sex 中女性的获救概率远远高于男性，毕竟在遇难时，女士和小孩先走。所以，Sex 是一个重要的特征。图 7 Sexyu Survived 关联性 (3) SibSp 与 Survived data_train[['SibSp', 'Survived']].groupby(['SibSp'], as_index=False).mean().sort_values(by='Survived', ascending=False) 兄弟姐妹个数似乎与 Survived 之间没有明显的关联，这个特征可以不用考虑。图 8 SibSp 与 Survived 关联性 (4) Parch 与 Survived data_train[['Parch', 'Survived']].groupby(['Parch'], as_index=False).mean().sort_values(by='Survived', ascending=False) 图 9 Parch 与 Survived 关联性

父母子女个数似乎与 Survived 之间也没有明显的关联，但是后期可以考虑合并 SibSp 和 Parch 两个特征建立一个新的特征 FamilySize。 (5) Embarked 与 Survived data_train[['Embarked', 'Survived']].groupby(['Embarked'], as_index=False).mean().sort_values(by='Survived', ascending=False) 图 10 Embarked 与 Survived 泰坦尼克号从英国的南安普顿港（S）出发，途径法国瑟堡（C）和爱尔兰昆士敦（Q），那么在昆士敦之前上船的人，有可能在瑟堡或昆士敦下船，这些人将不会遇到海难。由上可以看出，在不同的港口上船，生还率不同，C 最高，Q 次之，S 最低。所以，Embarked 也是一个重要的特征。 2.2.2 连续型特征与 survived 之间的关联性连续型特征与 survived 之间的关联性利用图来分析。首先导入画图需要的包： import seaborn as sns import matplotlib as plt (1) Age 与 Survived grid = sns.FacetGrid(data_train, 'Survived') grid.map(ply.hist, 'Age', bins=20) sns.set_style(darkgrid)#设置背景 plt.show() 图 11 Age 与 Survived 关联性

由图可知，婴儿（Age<4）的存活概率较大,年长者（Age=80）存活下来了,大部分青年（15-25）没有存活下来。Age 也是一个重要的特征。 (2) Age/Pclass 和 Survived grid = sns.FacetGrid(data_train, 'Survived', size=2.2, aspect=1.6) grid.map(plt.hist, 'Age', alpha=0.5, bins=20) sns.set_style('darkgrid') plt.show() 图 12 Age/Pclass 和 Survived 关联性根据上图，我们可知三点重要的信息： Pclass=1 中大部分乘客都存活下来了； Pclass=2 和 Pclass=3 中婴儿的存活概率较高； Pclass=3 的乘客最多，但是大部分都没有存活下下来。 (3) Embarked/Sex/Fare 和 Survived grid = sns.FacetGrid(data_train, row='Embarked', col='Survived', size=2.2, aspect=1.6) grid.map(sns.barplot, 'Sex', 'Fare', alpha=0.5, ci=None) sns.set_style('darkgrid') plt.show()

票价越高存活率越大，Embarked=C 中男性的存活率比较高，但可能与 Pclass 的特征相关。图 13 Embarked/Sex/Fare 和 Survived 关联性 (4) Cabin 与 Survived 属性里面缺失值较多，那我们先来看看有 Cabin 和没 Cabin 得乘客的获救情况是什么样的。 fig = plt.figure()fig.set(alpha=0.2)Survived_cabin = data_train.Survived[pd.notnull(data_train.Cabin)].value_counts()Survived_nocabin = data_train.Survived[pd.isnull(data_train.Cabin)].value_counts()df=pd.DataFrame({u'有 ':Survived_cabin, u'无':Survived_nocabin}).transpose()df.plot(kind='bar', stacked=True)plt.title(u"按 Cabin 有无看获救情况")plt.xlabel(u"Cabin 有无") plt.ylabel(u"人数")plt.show() 根据上图，有 Cabin 的似乎获救的概率要高一点。图 14 按 Cabin 有无看获救情况

分享到：

赞收藏

资料库

Kaggle Titanic项目报告；数据挖掘期末作业；.doc

相关推荐

人工智能

热门标签

最新资料