logo资料库

基于MATLAB语言环境的二阶惯性系统PID控制仿真.docx

发布时间：2022-06-14 发布人：admin 分类：说明书 资料大小：0.22M 资料格式：docx 举报 版权申诉
第1页 / 共15页
第2页 / 共15页
第3页 / 共15页
第4页 / 共15页
第5页 / 共15页
第6页 / 共15页
第7页 / 共15页
第8页 / 共15页
资料共15页，剩余部分请下载后查看
    基于 MATLAB 语言环境的二阶惯性系统 PID 控制仿真
    目录 一、课程设计要求……………………………………3 二、PID 控制简述……………………………………3 三、系统性能分析……………………………………5 四、参数整定…………………………………………6 五、PID 三参数变化对系统的影响……………………7 六、人机交互界面设计……………………………………9 七、心得体会………………………………15 2
    一、课程设计要求 1．在 MATLAB 语言环境下，给定参数下的二阶惯性系统，要求分析在单位阶跃函数作用 下，系统的动态响应性能； 2．在系统的前向通道加入比例、积分、微分控制器，调整系统控制器的比例、积分、微分 参数，需求系统的最佳输出性能； 3．利用所学知识分析三参数增大或减小时，对系统动静态性能的影响，并用仿真实验验证 其正确性。 4.设计人机交互界面，可通过对界面输入参数，实现参数修改于曲线显示。 注：二阶系统前向通道传递函数为 ( ) G s  0, b a  ( ) / ( as b cs  1, 100, c   2 d ds  4,   e ) e  80 。 二、PID 控制简述 PID 控制器由比例单元（P）、积分单元（I）和微分单元（D）组成。其输入 e (t)与输出 u (t)的关系为： u(t)=kp[e(t)+1/TI∫e(t)dt+TD*de(t)/dt] 式中积分的上下限分别是 0 和 t 。因 此它的传递函数为：G(s)=U(s)/E(s)=kp[1+1/(TI*s)+TD*s] 。其中 kp 为比例系数； TI 为积 分时间常数； TD 为微分时间常数。 比例(P)控制 比例控制是一种最简单的控制方式。其控制器的输出与输入误差信号成比例关系。当 仅有比例控制时系统输出存在稳态误差(ady-state error)。 积分(I)控制 在积分控制中，控制器的输出与输入误差信号的积分成正比关系。对一个自动控制系 统，如果在进入稳态后存在稳态误差，则这个控制系统是有稳态误差的或简称有差系统 (System with Steady-state Error)。为了消除稳态误差，在控制器中必须引入项”。积分项对误 差取决于时间的积分，随着时间的增加，积分项会增大。这样，即便误差很小，积分项也会 随着时间的增加而加大，推动控制器的输出增大使稳态误差进一步减小，直到等于零。因此， 比例+积分(PI)控制器，可以使系统在进入稳态后无稳态误差。 微分(D)控制 3
    在微分控制中，控制器的输出与输入误差信号的微分(即误差的变化率)成正比关系。自 动控制系统在克服误差的调节过程中能会出现振荡甚至失稳。其原因是由于存在有较大惯性 组件(环节)或有滞后(delay)组件，具有抑制误差的作用，其变化总是落后于误的变化。解决 的办法是使抑制误差的作用的变化“超前”，即在误差接近零时，抑制误差的作用就应该是 零。这就是说，在控制器中仅入“比例”项往往是不够的，比例项的作用仅是放大误差的幅 值，而目前需要增加的是“微分项”，它能预测误差变化的趋势，这样，有比例+微分的控 制器，就能够提前使抑制误差的控制作用等于零，甚至为负值，从而避免了被控量的严重超 调。所以对有较大惯性或滞的被控对象，比例+微分(PD)控制器能改善系统在调节过程中的 动态特性。 PID 控制器的参数整定 PID 控制器的参数整定是控制系统设计的核心内容。它是根据被控过程的特性确定 PID 控制器的比例系数、积分时间和微分时间大小。PID 控制器参数整定的方法很多，概括 起来有两大类：一是理论计算整定法。它主要是依据系统的数学模型，经过理论计算确定控 器参数。这种方法所得到的计算数据未必可以直接用，还必须通过工程实际进行调整和修改。 二是工程整定方法，它主要依赖工程经验，直接在控制系统的试验中进行，且方法简单、易 于掌握，在工程实际中被广泛采用。PID 控制器参数的工程整定方法，主要有临界比例法反 应曲线法和衰减法。三种方法各有其特点，其共同点都是通过试验，然后按照工程经验公式 对控制器参数进行整定。但无论采用哪一方法所得到的控制器参数，都需要在实际运行中进 行最后调整与完善。现在一般采用的是临界比例法。利用该方法进行 PID 整定步骤如下： (1)首先预选择一个足够短的采样周期让系统工作﹔ (2)仅加入比例控制环节，直到系统对输入的阶跃响应出现临界振荡，记下这时的比例 放大系数和临界振荡周期﹔ 4
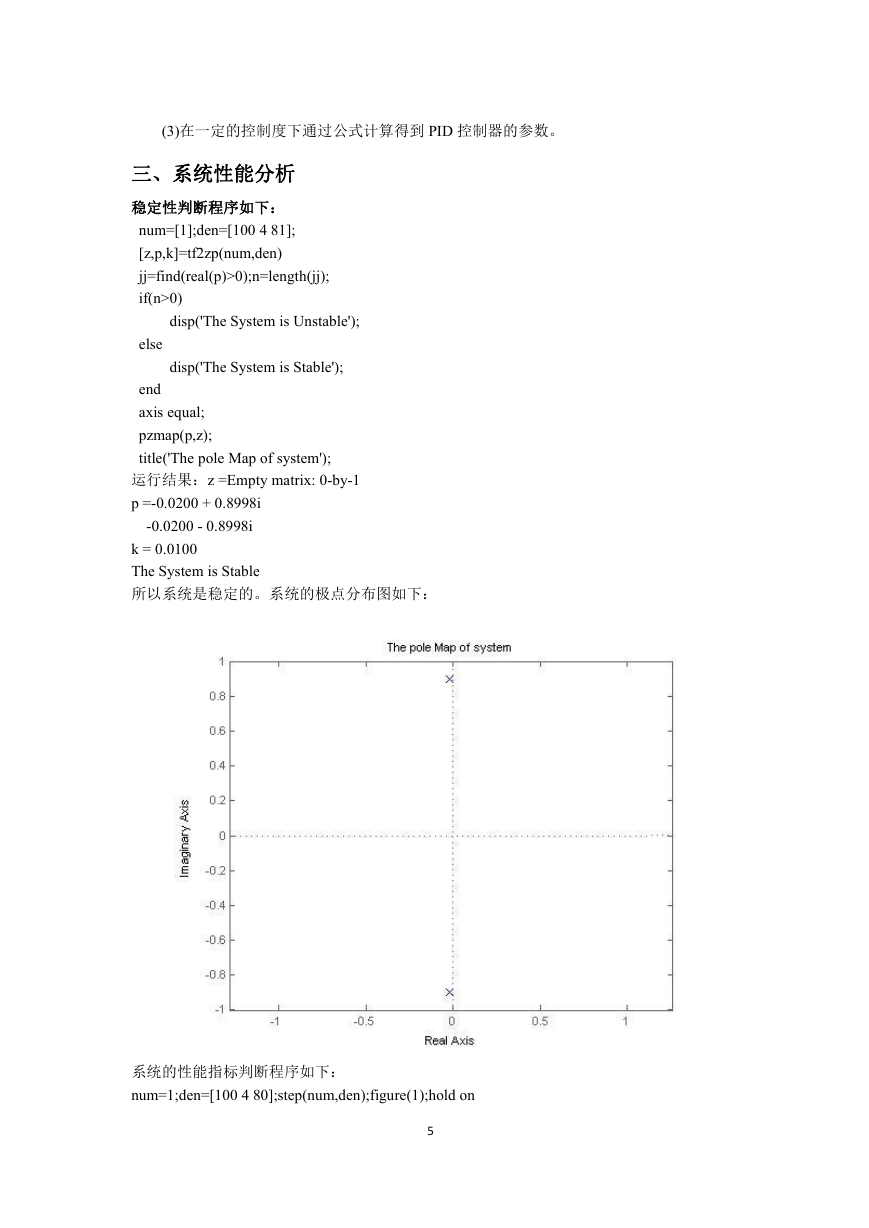
    (3)在一定的控制度下通过公式计算得到 PID 控制器的参数。 三、系统性能分析 稳定性判断程序如下： num=[1];den=[100 4 81]; [z,p,k]=tf2zp(num,den) jj=find(real(p)>0);n=length(jj); if(n>0) disp('The System is Unstable'); else disp('The System is Stable'); end axis equal; pzmap(p,z); title('The pole Map of system'); 运行结果：z =Empty matrix: 0-by-1 p =-0.0200 + 0.8998i -0.0200 - 0.8998i k = 0.0100 The System is Stable 所以系统是稳定的。系统的极点分布图如下： 系统的性能指标判断程序如下： num=1;den=[100 4 80];step(num,den);figure(1);hold on 5
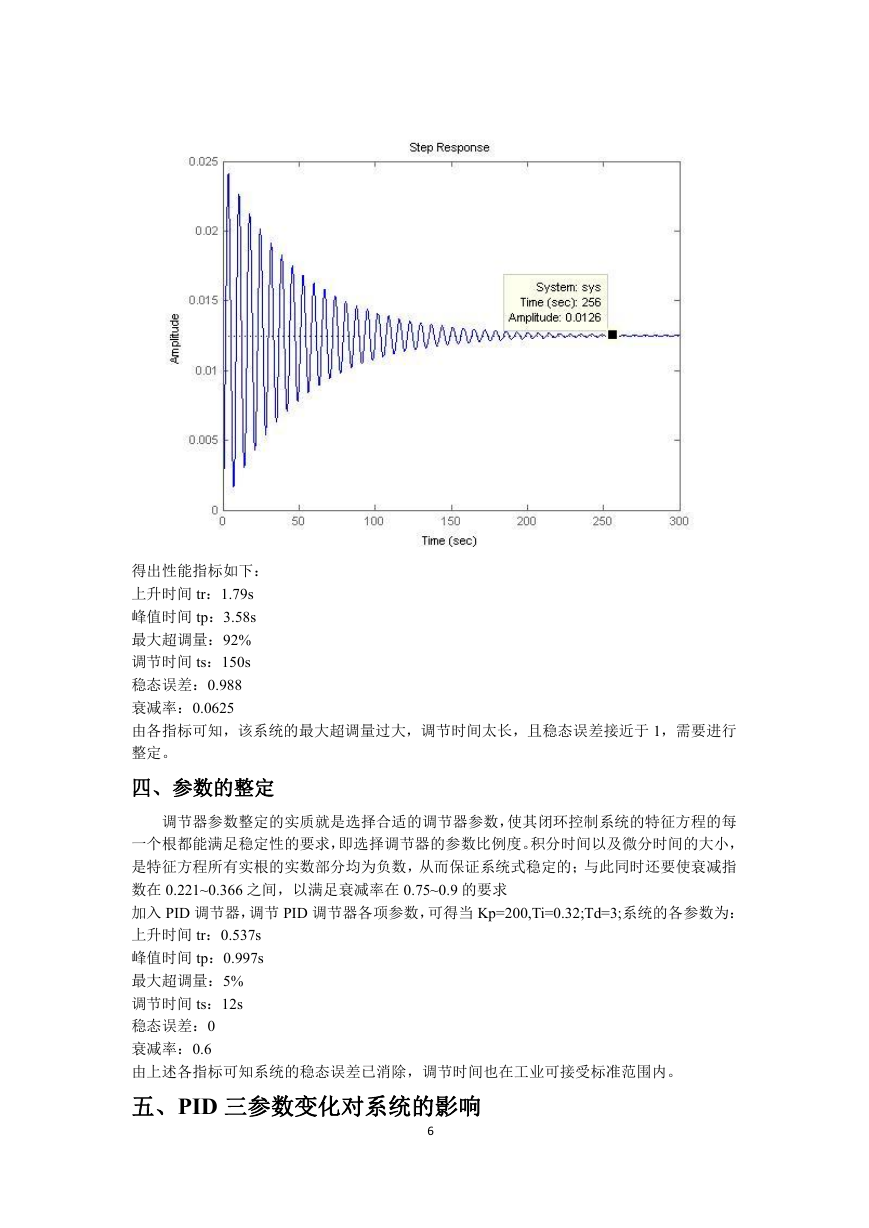
    得出性能指标如下： 上升时间 tr：1.79s 峰值时间 tp：3.58s 最大超调量：92% 调节时间 ts：150s 稳态误差：0.988 衰减率：0.0625 由各指标可知，该系统的最大超调量过大，调节时间太长，且稳态误差接近于 1，需要进行 整定。 四、参数的整定 调节器参数整定的实质就是选择合适的调节器参数，使其闭环控制系统的特征方程的每 一个根都能满足稳定性的要求，即选择调节器的参数比例度。积分时间以及微分时间的大小， 是特征方程所有实根的实数部分均为负数，从而保证系统式稳定的；与此同时还要使衰减指 数在 0.221~0.366 之间，以满足衰减率在 0.75~0.9 的要求 加入 PID 调节器，调节 PID 调节器各项参数，可得当 Kp=200,Ti=0.32;Td=3;系统的各参数为： 上升时间 tr：0.537s 峰值时间 tp：0.997s 最大超调量：5% 调节时间 ts：12s 稳态误差：0 衰减率：0.6 由上述各指标可知系统的稳态误差已消除，调节时间也在工业可接受标准范围内。 五、PID 三参数变化对系统的影响 6
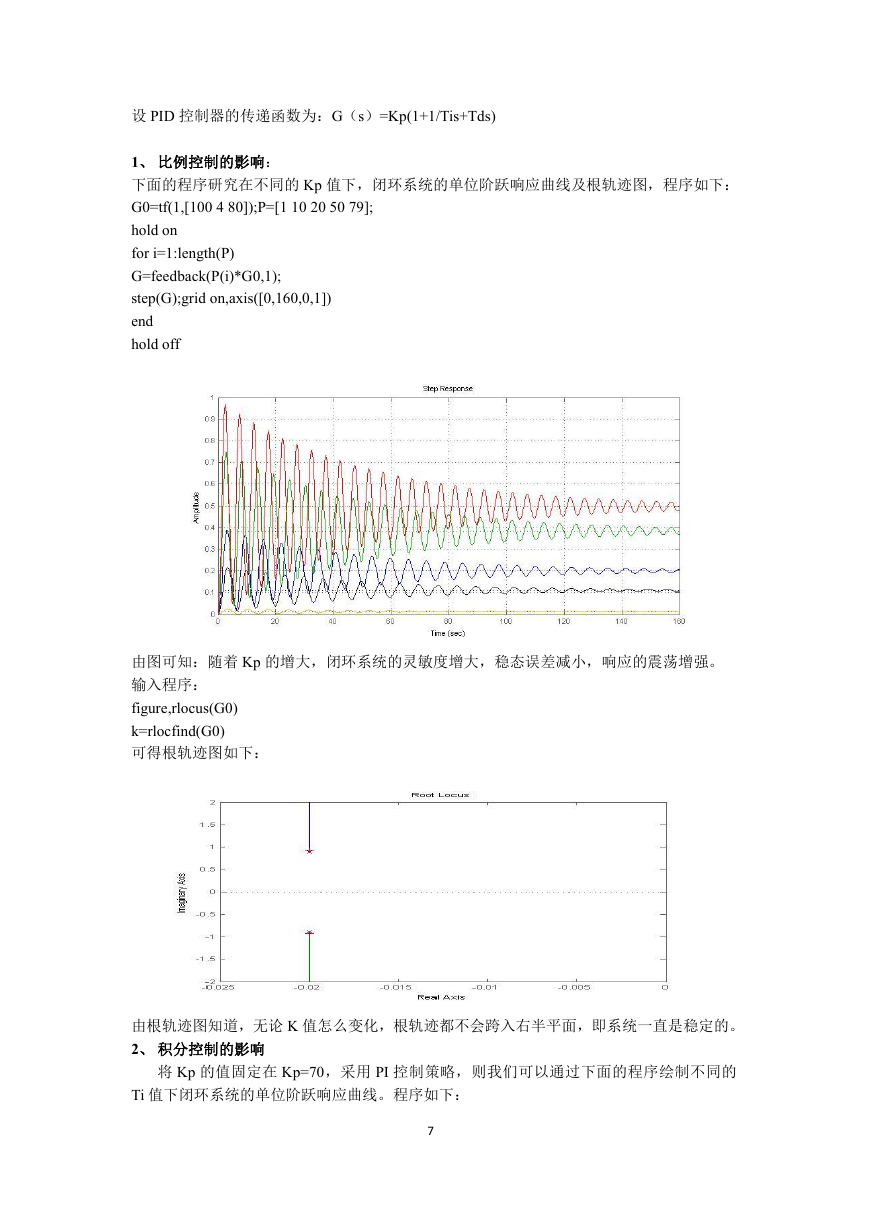
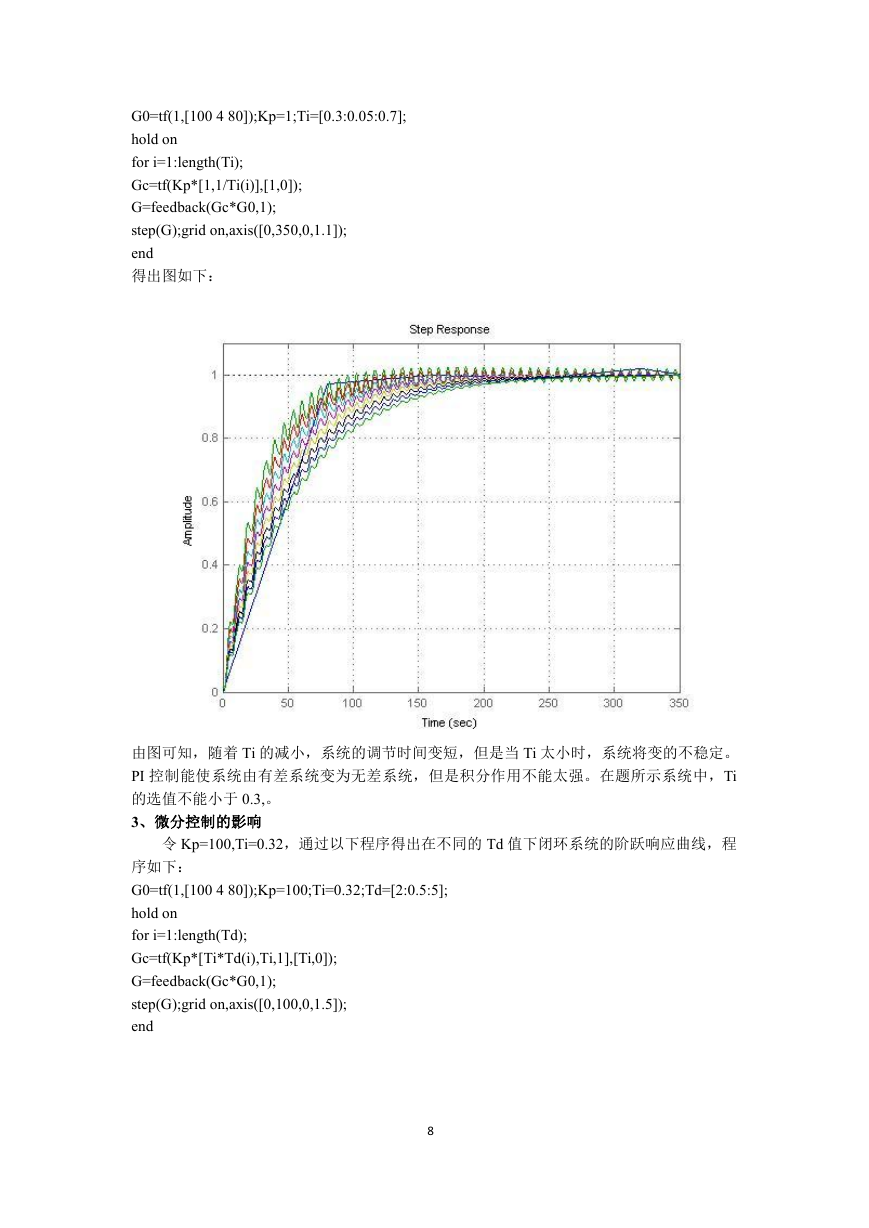
    设 PID 控制器的传递函数为：G（s）=Kp(1+1/Tis+Tds) 1、 比例控制的影响： 下面的程序研究在不同的 Kp 值下，闭环系统的单位阶跃响应曲线及根轨迹图，程序如下： G0=tf(1,[100 4 80]);P=[1 10 20 50 79]; hold on for i=1:length(P) G=feedback(P(i)*G0,1); step(G);grid on,axis([0,160,0,1]) end hold off 由图可知：随着 Kp 的增大，闭环系统的灵敏度增大，稳态误差减小，响应的震荡增强。 输入程序： figure,rlocus(G0) k=rlocfind(G0) 可得根轨迹图如下： 由根轨迹图知道，无论 K 值怎么变化，根轨迹都不会跨入右半平面，即系统一直是稳定的。 2、 积分控制的影响 将 Kp 的值固定在 Kp=70，采用 PI 控制策略，则我们可以通过下面的程序绘制不同的 Ti 值下闭环系统的单位阶跃响应曲线。程序如下： 7
    G0=tf(1,[100 4 80]);Kp=1;Ti=[0.3:0.05:0.7]; hold on for i=1:length(Ti); Gc=tf(Kp*[1,1/Ti(i)],[1,0]); G=feedback(Gc*G0,1); step(G);grid on,axis([0,350,0,1.1]); end 得出图如下： 由图可知，随着 Ti 的减小，系统的调节时间变短，但是当 Ti 太小时，系统将变的不稳定。 PI 控制能使系统由有差系统变为无差系统，但是积分作用不能太强。在题所示系统中，Ti 的选值不能小于 0.3,。 3、微分控制的影响 令 Kp=100,Ti=0.32，通过以下程序得出在不同的 Td 值下闭环系统的阶跃响应曲线，程 序如下： G0=tf(1,[100 4 80]);Kp=100;Ti=0.32;Td=[2:0.5:5]; hold on for i=1:length(Td); Gc=tf(Kp*[Ti*Td(i),Ti,1],[Ti,0]); G=feedback(Gc*G0,1); step(G);grid on,axis([0,100,0,1.5]); end 8
    分享到：
    赞 收藏

    相关推荐

    资料库

    开发技术

    共收录19306份资料，累计14个分类，关注成员有19位，主要包括：Actionscript,Javascript,PHP,VB,Perl,Delphi,Python,C#,C,Java,C++,Web开发,硬件开发,其它

    热门标签

    Actionscript Javascript PHP VB Perl Delphi Python C# C Java C++ Web开发 硬件开发 其它

    最新资料