模式识别中用近邻函数法进行聚类与分类.doc

发布时间：2022-05-31 发布人：admin 分类：说明书资料大小：0.12M 资料格式：doc 举报版权申诉

qq_33591755-10166728-4744302543363312310.doc.pdf-第1页.png

第1页 / 共5页

qq_33591755-10166728-4744302543363312310.doc.pdf-第2页.png

第2页 / 共5页

qq_33591755-10166728-4744302543363312310.doc.pdf-第3页.png

第3页 / 共5页

qq_33591755-10166728-4744302543363312310.doc.pdf-第4页.png

第4页 / 共5页

qq_33591755-10166728-4744302543363312310.doc.pdf-第5页.png

第5页 / 共5页

文本预览

模式识别考察卷应用题用近邻函数法进行聚类与分类一、原理及方法对于一个样本集中的任意两个样本 ix 和 jx ，如果 ix 是 jx 的第l 个近邻点，则定义 ix 对 . 定义 ix 和 jx 简的近邻函数值为 ),( id l j .样本间的近邻函数值越小，彼此越靠近，越相似。 jx 的近邻系数为 l ，记为 aij    ),( 2),( j id ijd 算法步骤如下： 1. 对于给定待分类的样本集合，计算距离矩阵 D ：  iD 其中 ),( , ( j i xxd , ( 为 ix 和 jx 的欧式距离。 i xxd ) ) j j 2. 用 D 计算近邻系数矩阵 M ，元素 ijM 为 ix 对 jx 的近邻系数。 3. 生成近邻函数矩阵 L ： 2  ),( iL 并置 L 对角线上元素为 N2 ，如果 ix 和 jx 有连接，则 ij MMj   ji ),( iL j 为连接损失。 4. 搜索矩阵 L ，将每个点与和它有最小近邻函数值的点连接起来，形成初始聚类。 5. 对已经分类的各类，计算各类的类内最大距离 dmin ,如果 ,则考虑合并类，反之聚类结果合理。当类数不变时，结束，反之， dmax ，类间最小距离 d min max  继续步骤 5。 d 二、数据原始数据为从不同生产线上收集的不同种类产品单个个体内的器件数，依据各种产品的器件数区间对其进行分类，数据如表 1 所示：表 1 各类产品质量数据序号生产线编号器件数序号生产线编号器件数 1 3 5 7 9 11 13 15 5 8 9 12 14 24 26 28 6 3 7 15 18 13 11 15 2 4 6 8 10 12 14 16 6 7 11 14 13 25 28 28 8 5 16 15 20 15 13 18 三、结果及分析

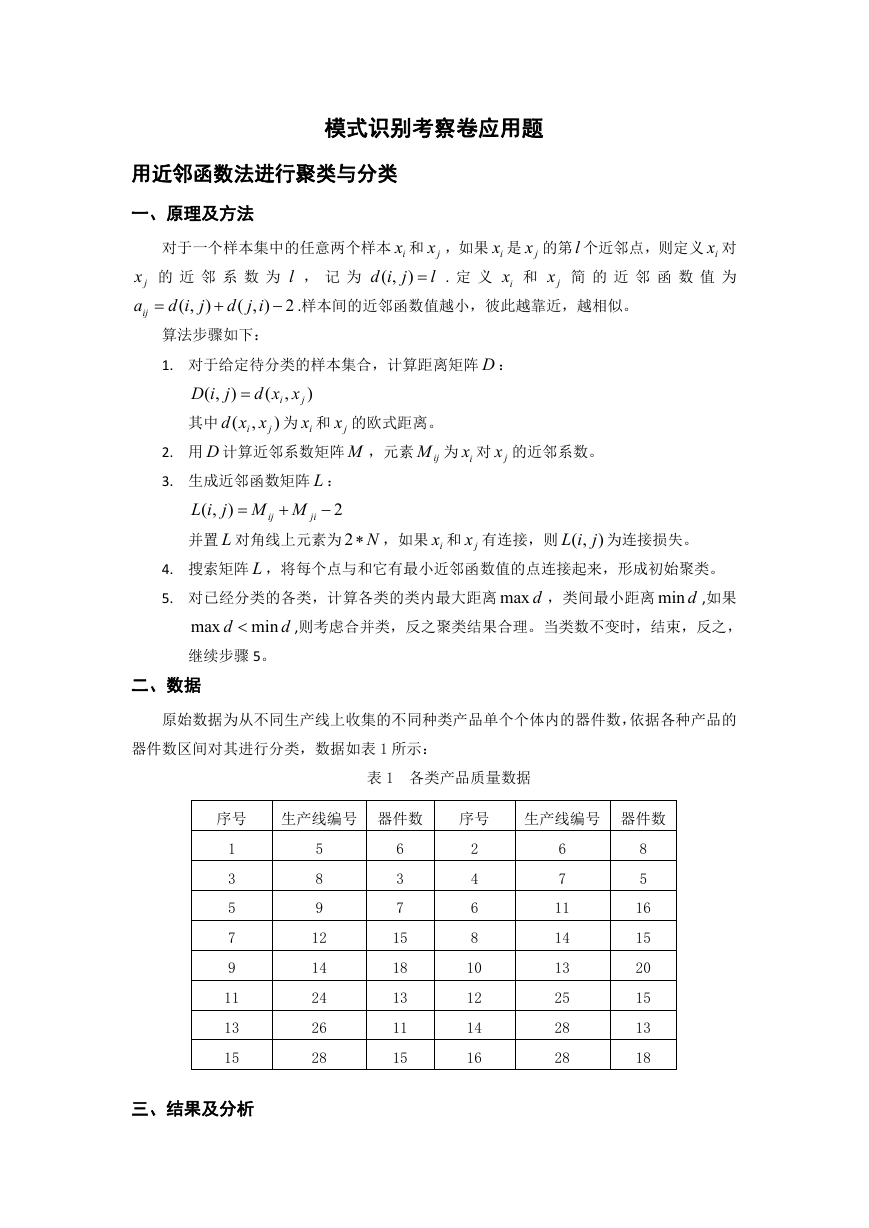
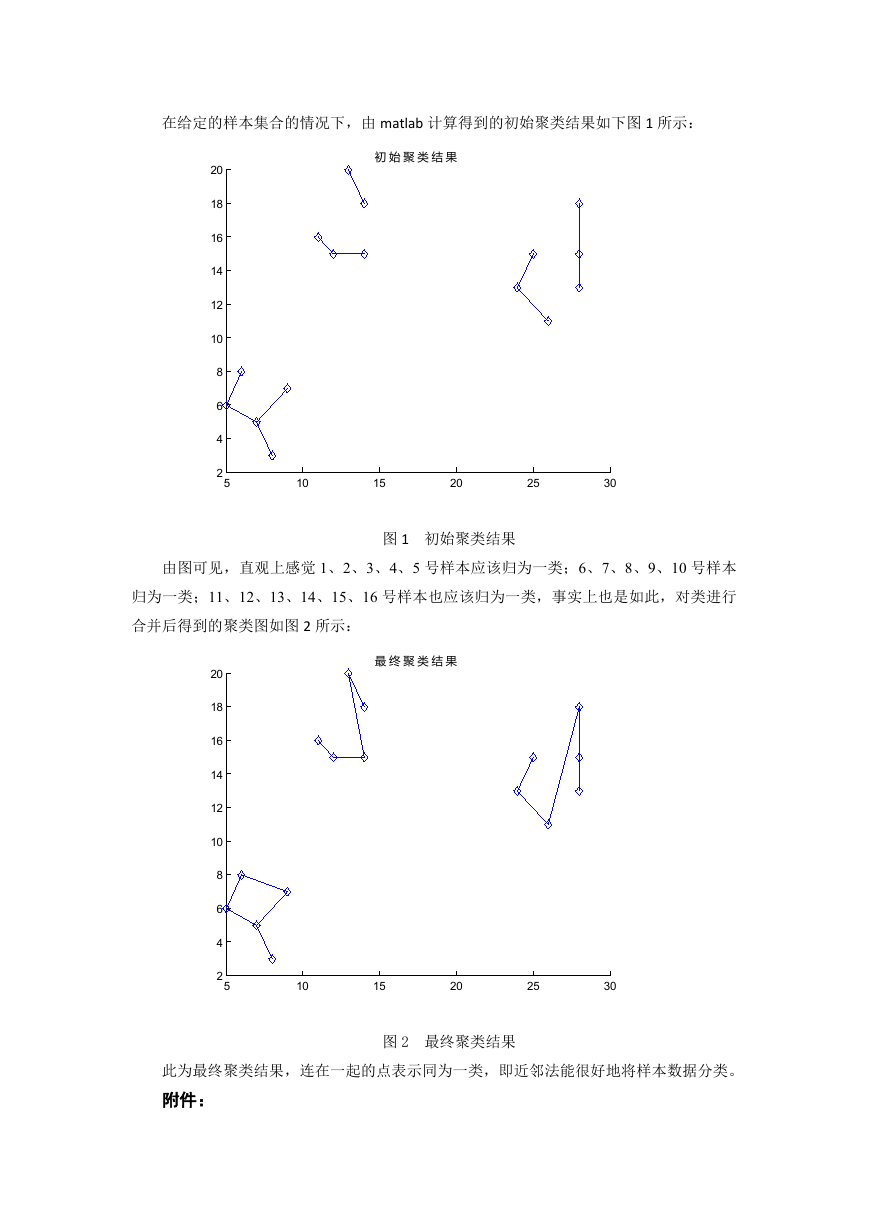
在给定的样本集合的情况下，由 matlab 计算得到的初始聚类结果如下图 1 所示： 20 18 16 14 12 10 8 6 4 2 5 初始聚类结果 10 15 20 25 30 图 1 初始聚类结果由图可见，直观上感觉 1、2、3、4、5 号样本应该归为一类；6、7、8、9、10 号样本归为一类；11、12、13、14、15、16 号样本也应该归为一类，事实上也是如此，对类进行合并后得到的聚类图如图 2 所示： 20 18 16 14 12 10 8 6 4 2 5 最终聚类结果 10 15 20 25 30 此为最终聚类结果，连在一起的点表示同为一类，即近邻法能很好地将样本数据分类。图 2 最终聚类结果附件：

clc,clear; sample=[5,6;6,8;8,3;7,5;9,7;11,16;12,15;14,15;14,18;13,20;24,13;25,15;26,11; 28,13;28,15;28,18]; m=size(sample,1); n=size(sample,2); D=zeros(m,m); L=zeros(m,m); %计算距离矩阵 D for i=1:m for j=1:m D(i,j)=sqrt((sample(i,:)-sample(j,:))*(sample(i,:)-sample(j,:))'); end end %计算近邻函数矩阵 M M=zeros(m,m); for i=1:m stmp=D(i,:); compare=D(i,:); for j=1:m for k=j:m if stmp(j)>stmp(k) swap=stmp(j); stmp(j)=stmp(k); stmp(k)=swap; end end jdex=find(compare==stmp(j)); if size(jdex,2)>1 jdex=jdex(1); end M(jdex,i)=j-1; compare(jdex)=-1; end end %计算矩阵 L for i=1:m for j=1:m if i==j L(i,j)=2*m; else L(i,j)=M(i,j)+M(j,i)-2; end end end

%扫描 L 矩阵，得到初始聚类 figure(1); title('初始聚类结果'); hold on; linkmark=zeros(m,m); cls=[];%用于保存聚类结果的数组,0 用来分隔不同类 for i=1:m index=find(L(i,:)==min(L(i,:))); if size(index,2)>1 index=index(1); end fi=any(cls==i); fin=any(cls==index); if(fi&(~fin)) cls=[cls,index]; end if((~fi)&fin) cls=[cls,i]; end if((~fi)&(~fin)) cls=[cls,0,i,index]; end plot([sample(i,1),sample(index,1)],[sample(i,2),sample(index,2)],'-d'); linkmark(i,index)=1;%表示 i,j 连接在一起 end cls=[cls,0];%作为标志便于提取各类元素 %合并类 clsn=size(find(cls==0),2)-1;%类别数 clsn %类成员 menber 和成员数 mn ind=zeros(1,clsn); flag=find(cls==0); md=max(diff(flag))-1; mn=diff(flag)-1; menber=zeros(clsn,md);%成员序号数组 for i=1:clsn menber(i,:)=[cls(flag(i)+1:flag(i+1)-1),zeros(1,md-mn(i))]; end %计算类内最大距离 ind for i=1:clsn ind(i)=0; if mn(i)>1 for j=1:mn(i)-1 for k=j+1:mn(i) if ind(i)

ind(i)=D(menber(i,j),menber(i,k)); end end end end end msgbox('回到 matlab 命令行模式下按任意键进行类合并'); pause; %比较类内最大距离和类间最小距离并合并类 title('最终聚类结果'); interd=zeros(clsn,clsn); for i=1:clsn-1 for j=i+1:clsn %求类间最小距离 interd interd(i,j)=D(menber(i,1),menber(j,1)); for p=1:mn(i) for q=1:mn(j) if interd(i,j)>D(menber(i,p),menber(j,q)) interd(i,j)=D(menber(i,p),menber(j,q)); end end end if (interd(i,j)

分享到：

赞收藏

资料库

模式识别中用近邻函数法进行聚类与分类.doc

相关推荐

人工智能

热门标签

最新资料