贝叶斯网络分析kaggle泰坦尼克号（Titanic）.pdf

发布时间：2022-05-31 发布人：admin 分类：说明书资料大小：0.39M 资料格式：pdf 举报版权申诉

qq_43497779-11967817-4744300845209725838.pdf-第1页.png

第1页 / 共6页

qq_43497779-11967817-4744300845209725838.pdf-第2页.png

第2页 / 共6页

qq_43497779-11967817-4744300845209725838.pdf-第3页.png

第3页 / 共6页

qq_43497779-11967817-4744300845209725838.pdf-第4页.png

第4页 / 共6页

qq_43497779-11967817-4744300845209725838.pdf-第5页.png

第5页 / 共6页

qq_43497779-11967817-4744300845209725838.pdf-第6页.png

第6页 / 共6页

贝叶斯网络分析kaggle泰坦尼克号（Titanic）

一、数据处理

1.原始数据分析

2.数据清洗

4.特征工程

二、贝叶斯网络搭建

1.设计贝叶斯网络

2.参数导入

3.推理

4.预测

三、问题

贝叶斯网络分析kaggle泰坦尼克号（Titanic）一、数据处理 1.原始数据分析主要是让参赛选手根据训练集中的乘客数据和存活情况进行建模，进而使用模型预测测试集中的乘客是否会存活。乘客特征总共有11个，以下列出。当然也可以根据情况自己生成新特征，这就是特征工程（feature engineering）要做的事情了。 PassengerId => 乘客ID Pclass => 客舱等级(1/2/3等舱位) Name => 乘客姓名 Sex => 性别 Age => 年龄 SibSp => 兄弟姐妹数/配偶数 Parch => 父母数/子女数 Ticket => 船票编号 Fare => 船票价格 Cabin => 客舱号 Embarked => 登船港口 2.数据清洗数据集合并 1 2 3 4 #合并训练集train和测试集test train=pd.read_csv('./train.csv') test=pd.read_csv('./test.csv') full=pd.concat([train,test],ignore_index=True)

查找缺失值 1 full.isnull().sum() 从缺失值来看，Embarked（登船港口）和Fare（船票价格）缺失值较少，Age与Cabin（客舱号）缺失较多，可能该特征对结果有较大的影响，将年龄与Cabin视作特征。 Age缺失值处理 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 full['Title']=full['Name'].apply(lambda x: x.split(',')[1].split('.') [0].strip()) full.Title.value_counts() def girl(aa): if (aa.Age!=999)&(aa.Title=='Miss')&(aa.Age<=14): return 'Girl' elif (aa.Age==999)&(aa.Title=='Miss')&(aa.Parch!=0): return 'Girl' else: return aa.Title full['Title']=full.apply(girl,axis=1) Tit=['Mr','Miss','Mrs','Master','Girl','Rareman','Rarewoman'] for i in Tit: full.loc[(full.Age==999)& (full.Title==i),'Age']=full.loc[full.Title==i,'Age'].median() 先根据‘Name’提取‘Title’，再用‘Title’的中位数对‘Age‘进行插补.先假设little girl都没结婚（一般情况下该假设都成立），所以little girl肯定都包含在Miss里面。little boy（Master）的年龄最大值为 14岁，所以相应的可以设定年龄小于等于14岁的Miss为little girl。至此数据缺失值处理完毕。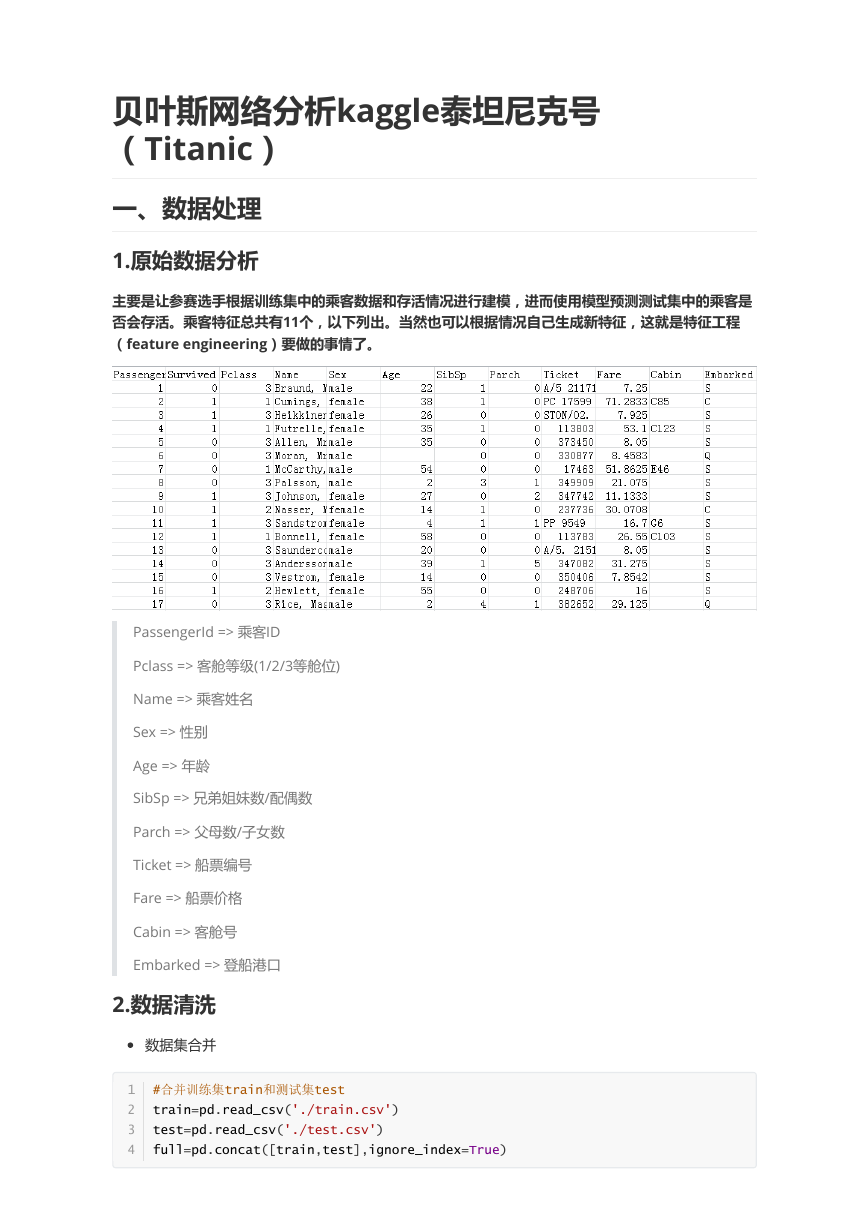 3.数据可视化性别对获救情况的影响 pd.crosstab(full.Sex,full.Survived).plot.bar(stacked=True,figsize= (8,5),color=['#4169E1','#FF00FF']) plt.xticks(rotation=0,size='large') plt.legend(bbox_to_anchor=(0.55,0.9)) 1 2 3

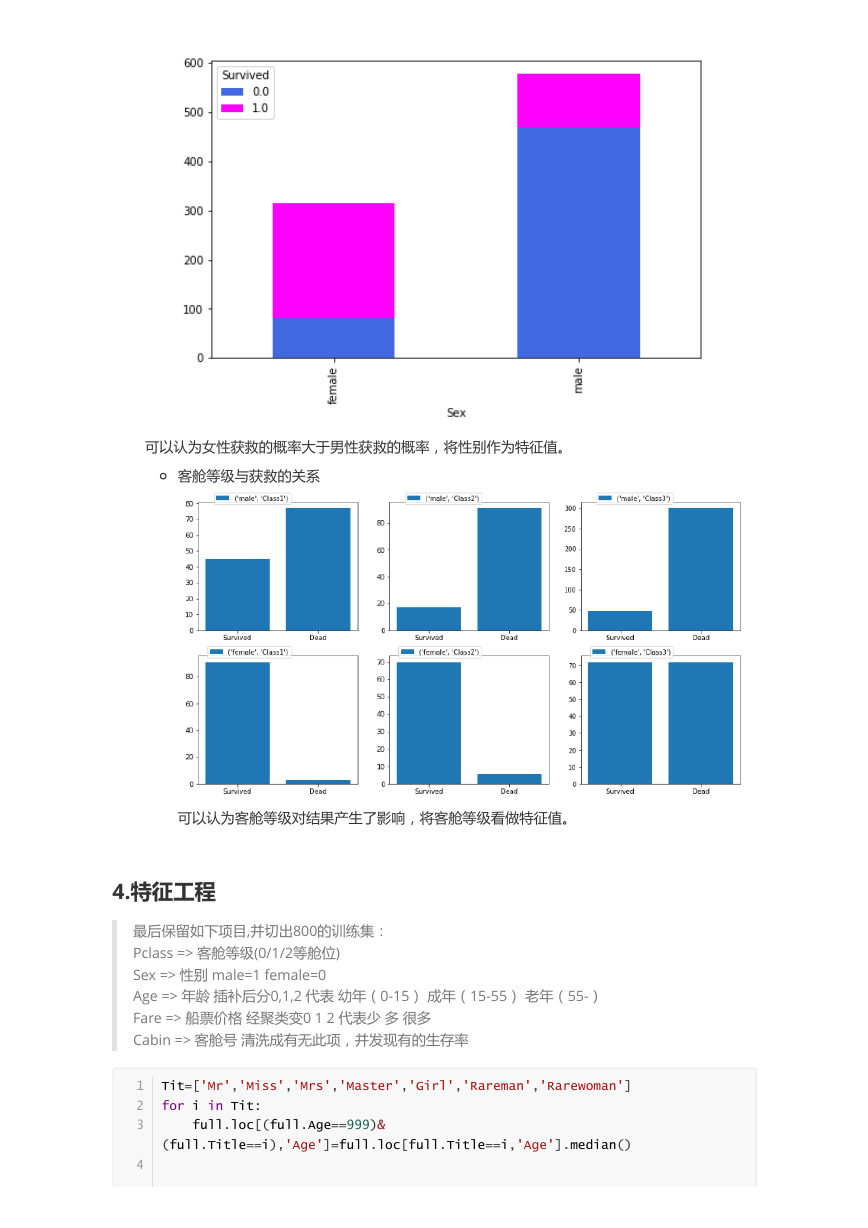
可以认为女性获救的概率大于男性获救的概率，将性别作为特征值。客舱等级与获救的关系可以认为客舱等级对结果产生了影响，将客舱等级看做特征值。 4.特征工程最后保留如下项目,并切出800的训练集： Pclass => 客舱等级(0/1/2等舱位) Sex => 性别 male=1 female=0 Age => 年龄插补后分0,1,2 代表幼年（0-15）成年（15-55）老年（55-） Fare => 船票价格经聚类变0 1 2 代表少多很多 Cabin => 客舱号清洗成有无此项，并发现有的生存率 1 2 3 4 Tit=['Mr','Miss','Mrs','Master','Girl','Rareman','Rarewoman'] for i in Tit: full.loc[(full.Age==999)& (full.Title==i),'Age']=full.loc[full.Title==i,'Age'].median()

5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 full.loc[full['Age']<=15,'Age']=0 full.loc[(full['Age']>15)&(full['Age']<55),'Age']=1 full.loc[full['Age']>=55,'Age']=2 full['Pclass']=full['Pclass']-1 from sklearn.cluster import KMeans Fare=full['Fare'].values Fare=Fare.reshape(-1,1) km = KMeans(n_clusters=3).fit(Fare) #将数据集分为2类 Fare = km.fit_predict(Fare) full['Fare']=Fare full['Fare']=full['Fare'].astype(int) full['Age']=full['Age'].astype(int) full['Cabin']=full['Cabin'].astype(int) full['Pclass']=full['Pclass'].astype(int) full['Sex']=full['Sex'].astype(int) #full['Survived']=full['Survived'].astype(int) dataset=full.drop(columns= ['Embarked','Name','Parch','PassengerId','SibSp','Ticket','Title']) dataset.dropna(inplace=True) dataset['Survived']=dataset['Survived'].astype(int) #dataset=pd.concat([dataset, pd.DataFrame(columns=['Pri'])]) train=dataset[:800] test=dataset[800:] 最后拿来的训练集train如下：二、贝叶斯网络搭建 1.设计贝叶斯网络

from pgmpy.models import BayesianModel from pgmpy.estimators import BayesianEstimator #model = BayesianModel([('Age', 'Pri'), ('Sex', 'Pri'),('Pri','Survived'), ('Fare','Pclass'),('Pclass','Survived'),('Cabin','Survived')]) model = BayesianModel([('Age', 'Survived'), ('Sex', 'Survived'), ('Fare','Pclass'),('Pclass','Survived'),('Cabin','Survived')]) 1 2 3 4 5 6 凭借对特征的理解，构建上图所示的有向图模型。 2.参数导入 1 model.fit(train, estimator=BayesianEstimator, prior_type="BDeu") 至此，模型构建完毕，开始进行推理。 3.推理 1 2 3 4 from pgmpy.inference import VariableElimination model_infer = VariableElimination(model) q = model_infer.query(variables=['Survived'], evidence={'Fare': 0}) print(q['Survived']) 得到一个Fare = 0时，P（Survived|Fare =0）的概率分布表。 4.预测 1 2 3 predict_data=test.drop(columns=['Survived'],axis=1) y_pred = model.predict(predict_data) print((y_pred['Survived']==test['Survived']).sum()/len(test))

得到预测的精度为：0.8131868131868132 三、问题概率图，贝叶斯网络的预测精度提升方法？当特征随机变量的值过多的时候，是否能通过概率图模型推理出精度较高的模型？

分享到：

赞收藏

资料库

贝叶斯网络分析kaggle泰坦尼克号（Titanic）.pdf

相关推荐

人工智能

热门标签

最新资料