62 2016，52（7） Computer Engineering and Applications 计算机工程与应用 实现苏拉卡尔塔棋网络博弈平台的吃子算法 张利群 ZHANG Liqun 辽宁石油化工大学 计算机与通信工程学院，辽宁 抚顺 113001 School of Computer and Communication Engineering, Liaoning Shihua University, Fushun, Liaoning 113001, China ZHANG Liqun. Realization of capture algorithm about Surakarta chess network battle platform in computer game. Computer Engineering and Applications, 2016, 52（7）：62-66. Abstract：Due to the demerit of needing manual intervention in the computer-computer game of Surakarta chess, the neces- sity of building a network battle platform in computer game is presented. The automatic game can be accomplished by the battle platform, and the capture algorithm is one of key technologies to build network game platform. Three key elements of Surakarta chess are introduced. A storage structure of realizing the battle platform in computer game of Surakarta chess is given out. Representation of board position is provided by using this storage structure. The capture circular queues are built, and the capture algorithm is implemented, thus the chess rule is realized. Experimental results show that the storage structure is efficient and reliable. The capture algorithm runs accurately. The capture algorithm can be applied to the build- ing of the Surakarta chess battle platform, and this storage structure and capture algorithm have referential value in design- ing the battle platform in computer game of other sorts of chesses. Key words：network battle; platform; storage structure; board position 摘 要：针对苏拉卡尔塔棋“机-机”博弈需要人工参与的弊端，提出了构建苏拉卡尔塔棋计算机网络博弈平台的必 要性，通过博弈平台实现自动对弈，而构建计算机博弈平台的核心技术之一就是吃子算法的实现。介绍了苏拉卡尔 塔棋的三个要素，给出了一种用于计算机博弈平台的苏拉卡尔塔棋的存储结构。使用这种结构，给出了棋局的表示 方法，建立了吃子循环队列，进而完成了适合于计算机博弈平台的吃子算法，实现了棋规。实验结果表明，这种存储 结构高效可靠，吃子算法运行正确。该吃子算法可以应用于苏拉卡尔塔棋博弈平台的构建，并且这种存储结构和吃 子算法对设计完成其他棋类的计算机博弈平台具有一定的参考价值。 关键词：网络博弈平台；存储结构；棋局 文献标志码：A 中图分类号：TP301.6 doi：10.3778/j.issn.1002-8331.1508-0122 1 引言 多年来，在全国大学生计算机博弈大赛暨全国计算 机博弈锦标赛中，参赛主体是代表队，各代表队主要来 自国内各高校、其他团体和个人。每个队由一名或多名 成 员 组 成 ，全 体 成 员 共 同 开 发 了 一 个 人 机 对 弈 程 序 。 2014 年全国大学生计算机博弈大赛暨全国计算机博弈 锦标赛比赛棋种共有 13 种，多数棋种也是国际计算机 奥林匹克大赛棋种[1-2]。 两个代表队之间的比赛是两个代表队的人机对弈 程序之间的博弈比赛，也就是两个机器之间的博弈，称 之为“机-机”博弈，“机-机”博弈是以操作者为中间媒介 实现的。如图 1 所示，假如程序甲先行棋，这时操作者 乙按程序甲的着法行棋，程序乙给出对应着法，这时操 程序甲 “机-机” 博弈 程序乙 操作者甲 操作者乙 图 1 “机-机”博弈 基金项目：辽宁省教育厅科学研究一般项目（No.L2013145）。 作者简介：张利群（1965—），男，教授，主要研究领域为机器博弈、计算机软件与理论，E-mail：zzllqun@163.com。 收稿日期：2015-08-13 修回日期：2015-11-03 文章编号：1002-8331（2016）07-0062-05 CNKI 网络优先出版：2015-11-09, http://www.cnki.net/kcms/detail/11.2127.TP.20151109.0905.012.html 

张利群：实现苏拉卡尔塔棋网络博弈平台的吃子算法 2016，52（7） 63 作者甲再按程序乙的着法行棋，如此反复进行下去，直 至博弈结束，通过人的参与实现了两个机器间的博弈。 （3）网络博弈平台不需要搜索引擎。 博弈平台模型如图 3 所示，其中图（a）是网络博弈 由于人的参与，出现了如下弊端[3]： （1）比赛双方需要人工查看对方行棋着法，费时且 容易出错； （2）比赛时，若采用双方软件中时钟，可能不准、对 方不信任以及作弊，若采用比赛时钟，由于需要人工查 看对方着法，时间上有误差； （3）每盘棋都需要裁判的监督，费时费力等。 如何解决这些弊端，途径只有一条，就是建立计算 机网络博弈平台，消除人工干预。 2 苏拉卡尔塔棋网络博弈平台简介 苏拉卡尔塔棋是国际计算机奥林匹克大赛和全国 大学生计算机博弈大赛棋种，它的棋盘也是全国大学生 计算机博弈大赛棋种中唯一的不规则棋盘。 2.1 苏拉卡尔塔棋简介 苏拉卡塔棋是一种两人玩的吃子类游戏，源自印尼 爪哇岛的苏拉卡尔塔（Surakarta）。棋盘由 6×6 正方形网 络与角落上的 8 个圆弧所组成，36 个交叉点为棋位。对 弈双方有两种不同颜色的棋子，各有 12 枚，常用的棋子 颜色为黑白两色。开始时，棋子在各方底线排成 2 排。 苏拉卡尔塔棋棋盘、棋子和开局状态如图 2 所示。 图 2 苏拉卡尔塔棋棋盘、棋子和开局状态 双方轮流走棋，每次走动一枚棋子，除了吃子之外， 每枚棋子只能沿着垂直或对角方向走动一格，只能走向 空位。吃掉对方棋子时必须经过至少一个完整的弧线， 并且在吃子的路径上没有棋子。吃掉所有对方棋子一 方获胜，或在限时比赛中，剩余棋子多的一方获胜。 2.2 网络博弈平台简介 计算机网络博弈平台实现的“机-机”博弈与人机对 弈软件有很大的不同，主要体现在以下几点： （1）网络博弈平台需要统一的博弈协议 [4-6]，一般的 人机对弈程序则不需要； （2）设计人机对弈程序时，移动的棋子、落子位置等 的获取需要用户单击或双击鼠标等动作获取，而网络博 弈平台只接收和发送相应的数据，全部是机器的处理， 没有用户的介入； 平台模型，图（b）是单机博弈平台模型。 博弈平台服务器 搜索引擎 1 搜索引擎 2 （a）网络模型 （b）单机模型 图 3 博弈平台模型 网络博弈平台模型是将来的发展方向，因为服务器 端和客户端可以在一个异构环境中正常工作。而单机 博弈平台模型限制了用户所使用的程序开发语言，不利 于推广。 在全国大学生计算机博弈大赛吃子类棋种中，苏拉 卡尔塔棋吃子算法最为特殊和复杂，其他 7 种棋类吃子 算法容易实现。通过查阅文献，尚未见到对苏拉卡尔塔 棋网络博弈平台吃子算法的研究。 3 苏拉卡尔塔棋在博弈平台上的存储结构 苏拉卡尔塔棋在网络博弈平台上的存储结构指的 是棋盘、棋子和棋局的存储结构。 3.1 棋盘的存储结构 虽然苏拉卡尔塔棋棋盘是个不规则棋盘，在棋盘的 每个角有 2 个弧线，4 个角共有 8 个弧线，但仍可以使用 1 个一维数组来存储棋盘[7-9]，其定义如下，下面所有表达 式和定义语句等均采用 C 语言来描述。 int a[36]； 也可以使用二维数组来存储棋盘[10]，其定如下： int b[6][6]； 实际的网络博弈平台程序中采用的是一维数组的 存储方法，这种存储结构存储了 36 个棋位。 8 个弧线可以用 8 个偶对来表示。 左上角 2 个弧线：（1，6），（2，12） 左下角 2 个弧线：（24，31），（18，32） 右上角 2 个弧线：（4，11），（3，17） 右下角 2 个弧线：（29，34），（23，33） 对于吃子，苏拉卡尔塔棋棋规有个规定，一方吃掉 另方棋子时必须经过至少一个弧线，基于上述存储结 构，网络博弈平台用两个循环队列表示棋盘中两个完整 轨道[11-13]。 利用这两个轨道，判定从起点位置到目标点位置是 否经历了 8 个偶对中的至少 1 个偶对，也就是是否经过 了弧线。 

64 2016，52（7） Computer Engineering and Applications 计算机工程与应用 两个循环队列定义如下： int cq1[24]； int cq2[24]； 在 cq1 中存放图 4 中蓝轨上的 24 个棋位，在 cq2 中 存放图 4 中绿轨上的 24 个棋位。因为是两个循环队列， 所以起始点可以是轨道上的任意棋位。 b[0][0]~b[0][5]：2，2，2，2，2，2 b[1][0]~b[1][5]：2，2，0，2，0，2 b[2][0]~b[2][5]：0，2，0，0，2，0 b[3][0]~b[3][5]：0，0，0，0，1，0 b[4][0]~b[4][5]：1，1，1，1，1，0 b[5][0]~b[5][5]：1，1，1，1，1，1 绿轨 蓝轨 4 吃子算法 吃子算法是实现苏拉卡尔塔棋网络博弈平台的 3 个 关键技术之一，除此之外，还有通信接口设计和博弈协 议的设计。 4.1 数组、变量的定义 算法中使用了如下数组和变量，其定义方法及作用 如表 1 所示。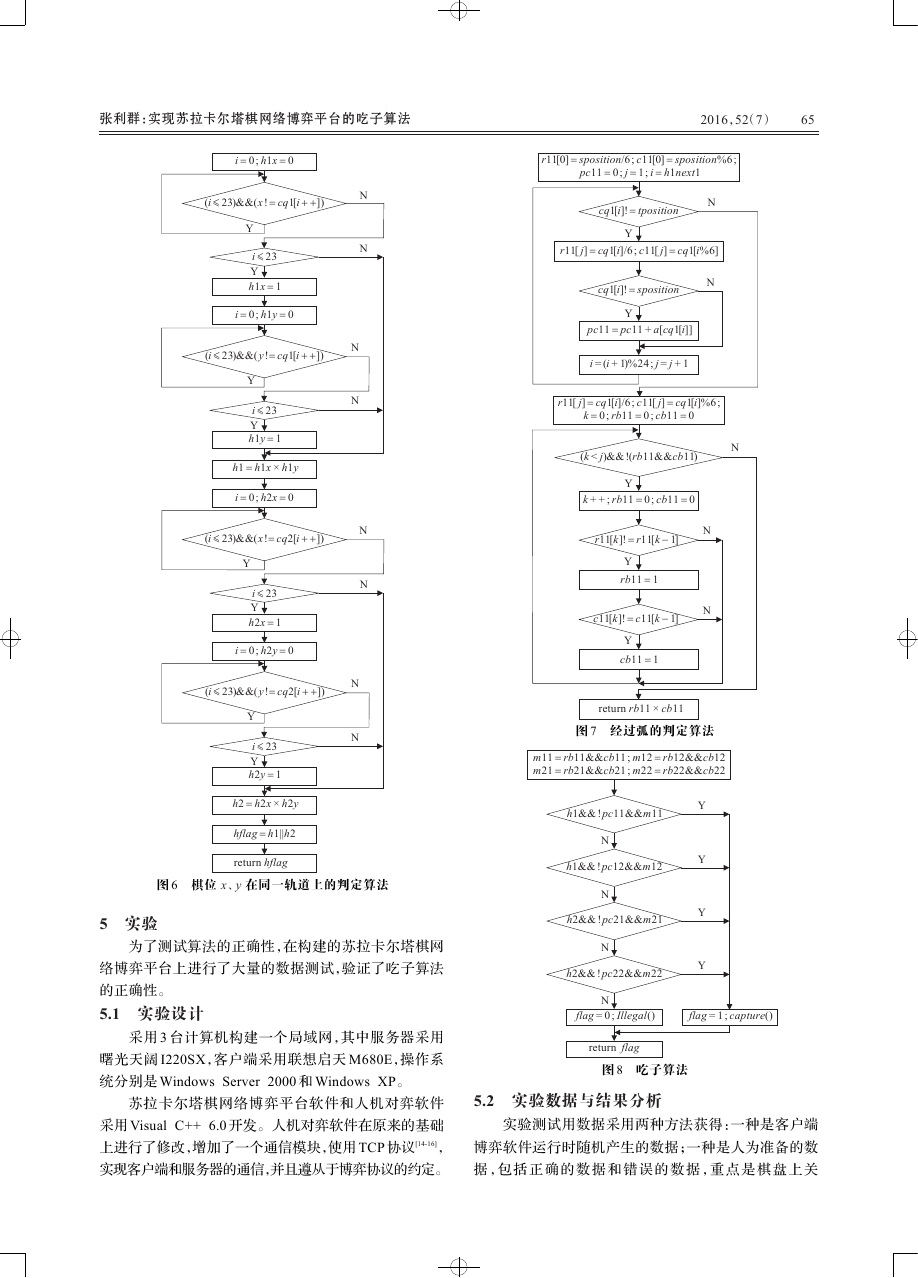 4.2 两个棋位在同一轨道上的判定算法 判 断 任 意 两 个 棋 位 x、y 在 同 一 轨 道 上 的 算 法 如 图 6 所示，若在同一轨道上，返回值为 1，否则为 0。 4.3 经过弧的判定算法 当判断出两个棋位在同一轨道上后，经过弧的判定 算法如图 7 所示。若经过弧线，返回值为 1，否则为 0。 限于篇幅，这里只给出了棋子在普通位置上 1 个方 向的经过弧的判定，相反方向的判定算法与此相似。在 两个轨道的交叉点位置，需要 4 个方向上的判断。 设 h1 = 1 若经过 cq1 循环队列所表示的轨道中的 任意一个弧，算法返回值为 1 的同时，也计算出了经过 轨道上的所有棋位棋子的表示值之和，并存放到变量 pc11 中。 4.4 吃子算法 利用前两个算法的结果，可以实现普通两点的吃子 算法，函数 capture( ) 表示吃子操作，函数 illegal( ) 表示 非法操作，吃子成功算法返回值为 1，算法主要部分如图 8 所示。 表 1 数组、变量的定义及其作用 作用 棋位 x、y 是否同时在蓝轨和绿轨上的逻辑值 蓝色轨道上普通棋位两个方向的下一个棋位的队列下标 蓝色轨道上特殊棋位另外两个方向的下一个棋位的队列下标 棋位 x、y 是否在蓝轨上的逻辑值 棋位 x、y 是否在绿轨上的逻辑值 普通变量 普通逻辑变量 吃子路径经过的棋位棋子值之和 存储轨道上棋位的行、列值 普通逻辑变量 普通逻辑变量 起点、落点的棋位值 任意两个棋位值 图 4 苏拉卡尔塔棋棋盘上的两个轨道 3.2 棋子的存储结构 棋子有两种颜色，不分兵种，每种 12 枚棋子。在存 储棋子时，一种颜色棋子可以用 1 表示，另一种颜色棋 子用 2 表示。在苏拉卡尔塔棋计算机网络博弈平台的 设计中，黑色棋子用 1 表示，白色棋子用 2 表示。 3.3 棋局的存储结构 假设有棋局如图 5 所示，使用一维数组 a 表示如下： a[0]到 a[35]的值依次为 2，2，2，2，2，2，2，2，0，2，0， 2，0，2，0，0，2，0，0，0，0，0，1，0，1，1，1，1，1，0，1，1，1，1， 1，1。 图 5 棋局状态图 使用二维数组 b 表示如下： 定义 int h1h2 int h1next1h1next2 int h1next3h1next4 int h1xh1y int h2xh2y int ijk int m11m12m21m22 int pc11pc12pc21pc22 int r11[24]c11[24] int rb11cb11rb12cb12hflag int rb21cb21rb22cb22flag int spositiontposition int xy 

张利群：实现苏拉卡尔塔棋网络博弈平台的吃子算法 2016，52（7） 65 N N N N N N N N i = 0; h1x = 0 (i  23)&&(x! = cq1[i + +]) Y i  23 Y h1x = 1 i = 0; h1y = 0 (i  23)&&(y!= cq1[i + +]) Y i  23 Y h1y = 1 h1 = h1x × h1y i = 0; h2x = 0 (i  23)&&(x!= cq2[i + +]) Y i  23 Y h2x = 1 i = 0; h2y = 0 (i  23)&&(y!= cq2[i + +]) Y i  23 Y h2y = 1 h2 = h2x × h2y hflag = h1||h2 return hflag 图 6 棋位 x、y 在同一轨道上的判定算法 5 实验 为了测试算法的正确性，在构建的苏拉卡尔塔棋网 络博弈平台上进行了大量的数据测试，验证了吃子算法 的正确性。 5.1 实验设计 采用 3 台计算机构建一个局域网，其中服务器采用 曙光天阔 I220SX，客户端采用联想启天 M680E，操作系 统分别是 Windows Server 2000 和 Windows XP。 苏拉卡尔塔棋网络博弈平台软件和人机对弈软件 采用 Visual C++ 6.0 开发。人机对弈软件在原来的基础 上进行了修改，增加了一个通信模块，使用 TCP 协议[14-16]， 实现客户端和服务器的通信，并且遵从于博弈协议的约定。 r11[0] = sposition/6; c11[0] = sposition%6; pc11 = 0; j = 1; i = h1next1 cq1[i]! = tposition N Y r11[ j] = cq1[i]/6; c11[ j] = cq1[i%6] cq1[i]! = sposition N Y pc11 = pc11 + a[cq1[i]] i = (i + 1)%24; j = j + 1 r11[ j] = cq1[i]/6; c11[ j] = cq1[i]%6; k = 0; rb11 = 0; cb11 = 0 N (k < j)&& !(rb11&&cb11) Y k + + ; rb11 = 0; cb11 = 0 N N r11[k]! = r11[k - 1] Y rb11 = 1 c11[k]! = c11[k - 1] Y cb11 = 1 return rb11 × cb11 图 7 经过弧的判定算法 m11 = rb11&&cb11; m12 = rb12&&cb12 m21 = rb21&&cb21; m22 = rb22&&cb22 h1&& !pc11&&m11 N h1&& !pc12&&m12 N h2&& !pc21&&m21 N h2&& !pc22&&m22 N Y Y Y Y flag = 0; Illegal() flag = 1; capture() return flag 图 8 吃子算法 5.2 实验数据与结果分析 实验测试用数据采用两种方法获得：一种是客户端 博弈软件运行时随机产生的数据；一种是人为准备的数 据 ，包 括 正 确 的 数 据 和 错 误 的 数 据 ，重 点 是 棋 盘 上 关 

66 2016，52（7） Computer Engineering and Applications 计算机工程与应用 键位置的数据，例如图 9 中所展示的关键位置数据的 测试。 T S （a）蓝轨上的吃子 T S （b）绿轨到蓝轨的吃子 S T S T （c）绿轨上的吃子 （d）仅经过弧的吃子 图 9 棋盘上关键点位置 实验结果表明，用 Visual C++ 6.0 实现的苏拉卡尔 塔棋网络博弈平台，对棋局的存储结构高效可靠，用循 环队列来表示弧线准确可行，实现的吃子算法运行正 确，博弈平台性能好，具有很好的容错特性。 6 结束语 苏拉卡尔塔棋棋盘是不规则棋盘，在实现苏拉卡尔 塔棋计算机网络博弈平台程序时，有多种存储结构可以 选择。本文研究了苏拉卡尔塔棋的逻辑结构，提出了存 储苏拉卡尔塔棋棋盘、棋子和棋局的具体方法。在这种 最普通的物理结构基础上，实现了网络博弈平台上的吃 子算法。 事实上，可以进一步修改循环队列所存储数据的数 据类型，使它包含更多的数据信息，这样就可以使相应 算法的实现进一步简化。 参考文献： [1] Gao Qiang，Xu Xinhe.The NSCGT-CCGC computer games tournament[J].International Computer Games Association Journal，2013，36（4）：252-254. [2] Tong Guofeng，Xu Xinhe.Progress of computer games in China[J].International Computer Games Association Journal，2011，34（3）：168-170. [3] Zhang Liqun，Ding Lili，Li Zhenlai.Research on the battle platform in computer game[C]//Proceedings of the 24th and Decision Conference.Piscataway， Chinese Control NJ：IEEE Press，2012：1513-1516. [4] Zhang Liqun，Ding Lili，Li Zhenla.The design of surakarta chess battle platform in computer game[C]//Proceedings of the 25th Chinese Control and Decision Conference. Piscataway，NJ：IEEE Press，2013：2332-2335. [5] 刘知青，李文峰.现代计算机围棋基础[M].北京：北京邮电 大学出版社，2011：181-184. [6] 徐心和，徐长明.计算机博弈原理与方法学概述[C]//中国 人工智能进展会议，2009：1-13. [7] Yen Shijim，Chou Chengwei，Chen Jrchang，et al.Design and implementation of Chinese Dark Chess programs[J]. IEEE Transactions on Computational Intelligence and AI in Games，2015，7（1）：66-74. [8] 徐心和，王骄.中国象棋计算机博弈关键技术分析[J].小型 微型计算机系统，2006，27（6）：961-969. [9] 周玮，王水涛，孙旸.中国象棋计算机博弈中的一种数据结 构方法[J].计算机工程与应用，2006，42（35）：219-221. [10] 张利群.五道棋计算机博弈程序的设计与实现[J].计算机 工程，2010，36（10）：221-222. [11] Silvela J，Portillo J.Breadth-first search and its applica- tion to image processing problems[J].IEEE Transac- tions on Image Processing，2001，10（8）：1194-1199. [12] 唐策善，黄刘生.数据结构[M].合肥：中国科学技术大学出 版社，1992：67-76. [13] Yang Yang，Cui Huimin，Feng Xiaobing，et al.A hybrid iterative stencil computa- and circular queue method for tions on GPUs[J].Journal of Computer Science Technology，2012，27（1）：57-74. [14] Nikitinskiy M A，Chalyy D J.Performance analysis of trickles and TCP transport protocols under high-load network conditions[J].Automatic Control and Computer Sciences，2013，47（7）：359-365. [15] Anurag K.Comparative performance analysis of ver- sions of TCP in a local network with a lossy link[J]. IEEE/ACM Transactions on Networking，1998，6（4）： 485-498. [16] Chandra K，Rich W.Using JavaNws to compare C and Java TCP-socket performance[J].Concurrency Computa- tion Practice and Experience，2001，13（8/9）：815-839.