第1页 / 共7页
第2页 / 共7页
第3页 / 共7页
第4页 / 共7页
第5页 / 共7页
第6页 / 共7页
第7页 / 共7页
数值分析插值法实验报告.doc
成都信息工程大学计算机学院
数值分析实验报告
插值法实验
姓
学
班
名：
号：
级：
完成日期：
任课教师：
张健
2015051122
计算机应用 152 班
2018 年 3 月 21 日
陈俊副教授
1
实验一 插值法实验
一、 实验目的
1.用 多 项 式 插 值 法 问 题 进 行 模 拟 和 预 测 ；
2 比 较 用 不 同 次 数 的 插 值 多 项 式 对 问 题 进 行 预 测 的 效 果 ；
3 根 据 (2)中 比 较 的 结 果 说 明 用 多 项 式 插 值 对 问 题 进 行 预 测 的 局 限 性 。
二、 实验题目
1.用表 1-1 中的世界人口统计数值估计 1980 年的人口
表 1-1
年
1960
1970
1990
2000
人口
3 039 585 530
3 707 475 887
5 281 653 820
6 079 603 571
要求:
(a) 采用经过 1970 和 1990 年估计值的直线；
(b) 经过 1960 年、1970 年以及 1990 年估计值的抛物线；
(c) 经过全部 4 个数据点的三次曲线。
并分别与 1980 年的人口估计值 4 452 584 592 进行比较。
2. 世界石油产量以每天百万桶计，如表 1-2 所示。估计 2010 年的石油产量。
(a) 采用线性插值；
(b) 采用经过全部数据点的 9 次多项式。
在这个例子里，哪个 2010 年石油产量的估计值是更合理。你以为插值多项式是数据的好
模型吗？请解释之.
年
1994
1995
1996
1997
1998
表 1-2
桶/天(×106)
67.052
68.008
69.803
72.024
73.400
年
1999
2000
2001
2002
2003
桶/天(×106)
72.063
74.669
74.487
74.065
76.777
三、 实验原理
1. 拉 格 朗 日 插 值
在 实 际应 用 中 ，一 般 采用 基 函 数 法 来构 造 插 值 函数 。将n次 拉 格朗 日 插 值 多 项式
2
用 ( )
nL x 来 记。设
( )
L x
n
( )
l x y
0
0
( )
l x y
1
1
( )
l x y
n
n
待 定 的n次 多 项式 。
，其 中 0
l x
( ) ,
( ) ,
l x
1
( )
l x
,
n
是
由 于 ( )
nL x 要 满 足插 值 条 件 (
L x
i
n
1
j
0
j
(
l x
i
)
j
)
y
i
(
i
0,1,
,
n
)
， 自 然地 求
i
i
(
i
,
j
0,1,
,
n
)
,
,
,
,
x
,
x
,
x
x
1
1
i
(
A x
x
显 然 ， 0
1
i
( )
l x
i
是 ( )
)
il x 的 零 点， 于 是
x
x
1
i
由 于 这一 多 项 式 已 经是n次 的 ，这 里 的 A 为 待 定常 数 。
利 用 条件 (
l x ， 可 得
i
) 1
(
n
)(
)(
x
i
x
0
x
x
x
1
i
)
(
x
x
n
)
1
A
(
x
i
x
0
)(
x
i
x
1
)
(
x
i
1
x
i
)(
x
i
x
i
1
)
(
x
i
x
n
)
1
于 是
( )
l x
i
(
x
i
)(
x
x
x
0
)(
x
x
0
i
)
(
x
x
1
)
(
x
x
1
i
(
x
i
x
i
1
1
)
)(
x
)(
x
i
x
1
i
x
i
1
(
)
x
(
x
i
)
x
n
x
n
)
(1)在 计 算机 上 构 造 拉 格朗 日 插 值 多 项式 ， 采 用 以 下式 子 进 行 编 程
( )
l x
i
n
x
x
i
j
j
0
i
x
j
x
j
(
i
0 ,1,
,
n
)
( )
L x
n
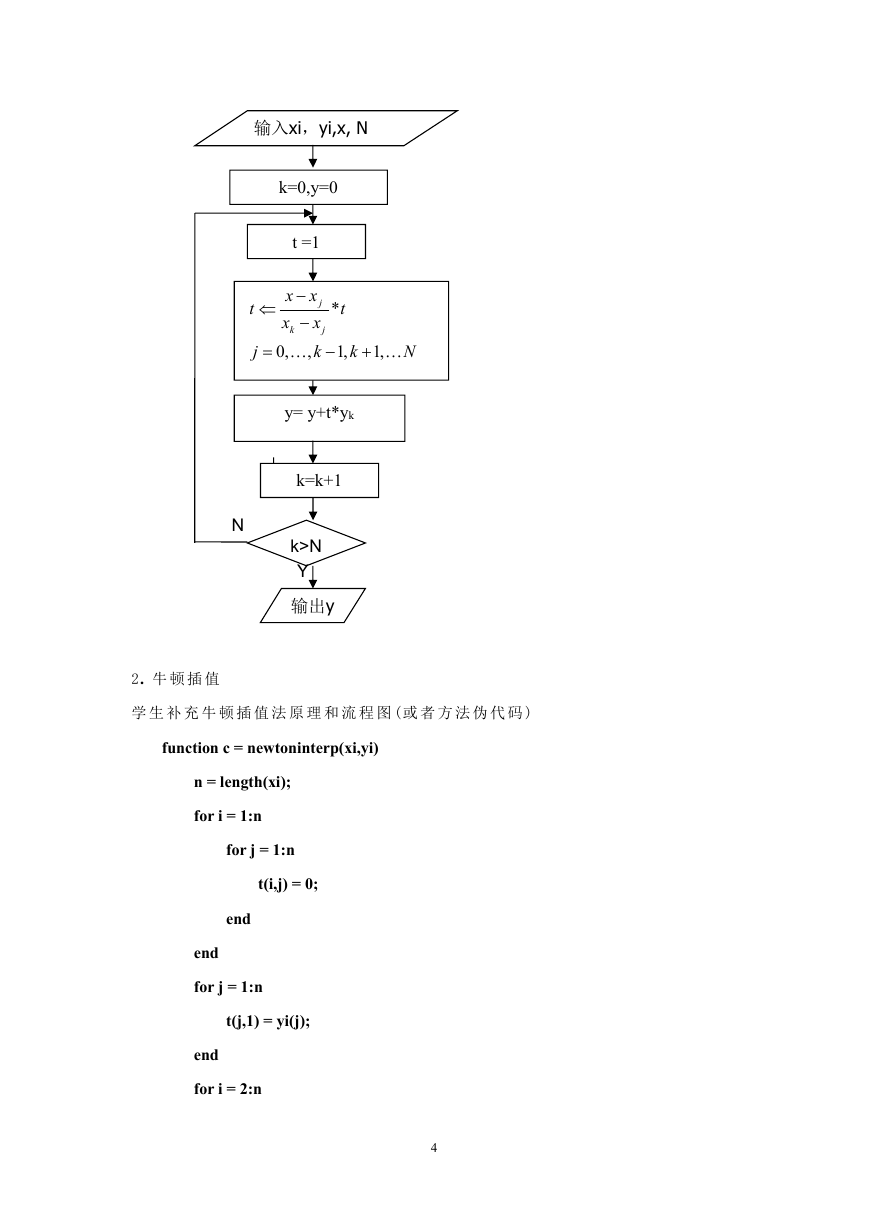
(2)Lagrange插 值 法 计 算 的程 序 框 图
n
i
0
( )
l x y
i
i
3
输入xi，yi,x, N
k=0,y=0
t =1
t
j
x
x
k
,
0,
Y
x
j
x
k
j
*
t
N
1,
k
1,
N
y= y+t*yk
k=k+1
k>N
Y
输出y
N
2. 牛 顿 插 值
学 生 补 充 牛 顿 插 值 法 原 理 和 流 程 图 (或 者 方 法 伪 代 码 )
function c = newtoninterp(xi,yi)
n = length(xi);
for i = 1:n
for j = 1:n
t(i,j) = 0;
end
end
for j = 1:n
t(j,1) = yi(j);
end
for i = 2:n
4
for j = i:n
t(j,i) = (t(j,i -1) - t(j - 1,i - 1))/(xi(j) - xi(j - i + 1));
end
end
for i = 1:n
c(i) = t(i,i);
end
end
四、 实验内容与结果
实验题目 1
(1) 程序代码：
function v = Lagrange(x,y,u)
n = length(x);
v = zeros(size(u));
for k = 1:n
w = ones(size(u));
for j = [1:k-1 k+1:n]
w = (u - x(j))./(x(k) - x(j)).*w;
end
v = v + w * y(k);
end
end
x=[1960,1970,1990,2000];
y=[3039585530,3707475887,5281653820,6079603571];
xi=1980
poly=LagrangePoly(x,y)
5
yi=subs(poly,'t',xi)
plot(x,y,'o',xi,yi,'*');
plot(x,y,'o',xi,yi,'*',x,y);
(2) 计算结果、图与分析
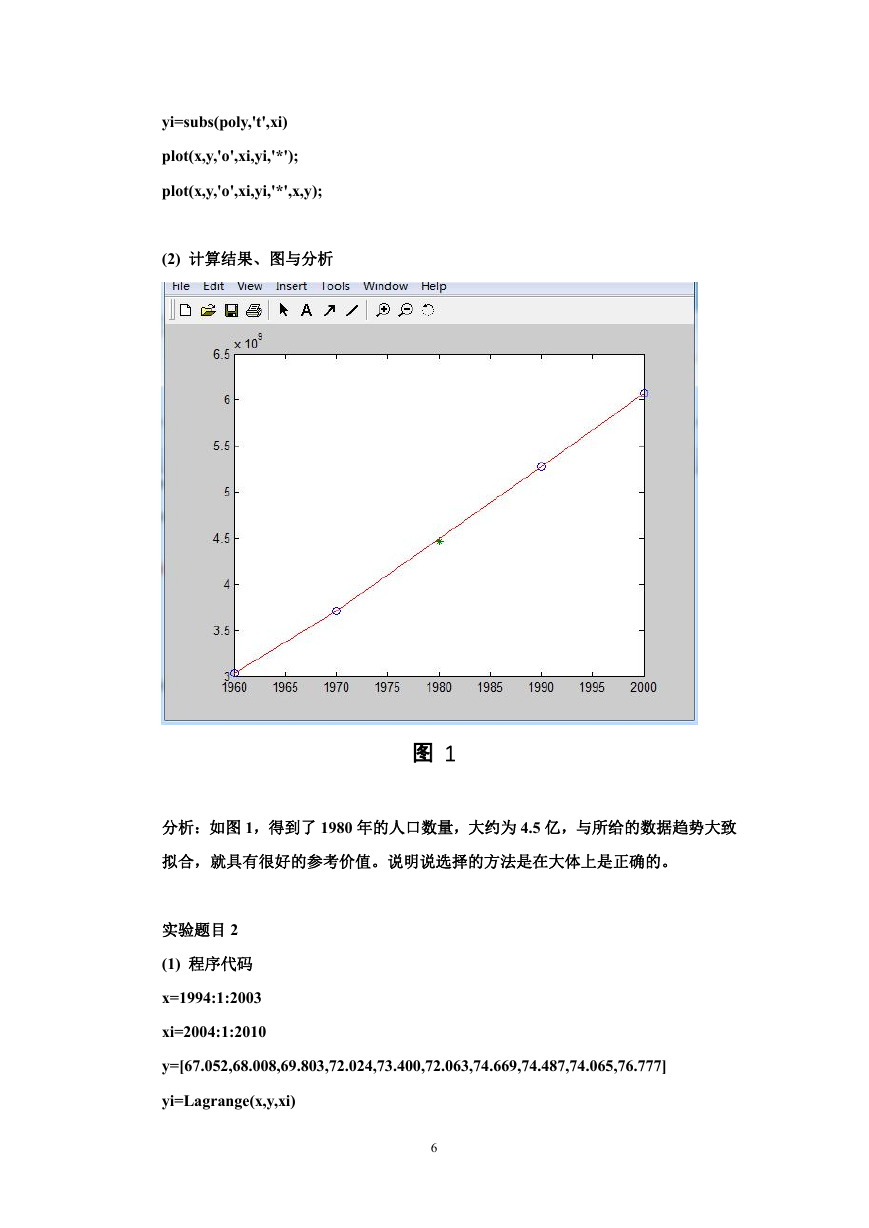
图 1
分析：如图 1，得到了 1980 年的人口数量，大约为 4.5 亿，与所给的数据趋势大致
拟合，就具有很好的参考价值。说明说选择的方法是在大体上是正确的。
实验题目 2
(1) 程序代码
x=1994:1:2003
xi=2004:1:2010
y=[67.052,68.008,69.803,72.024,73.400,72.063,74.669,74.487,74.065,76.777]
yi=Lagrange(x,y,xi)
6
plot(x,y,'o',xi,yi,'*');
(2) 计算结果、图与分析
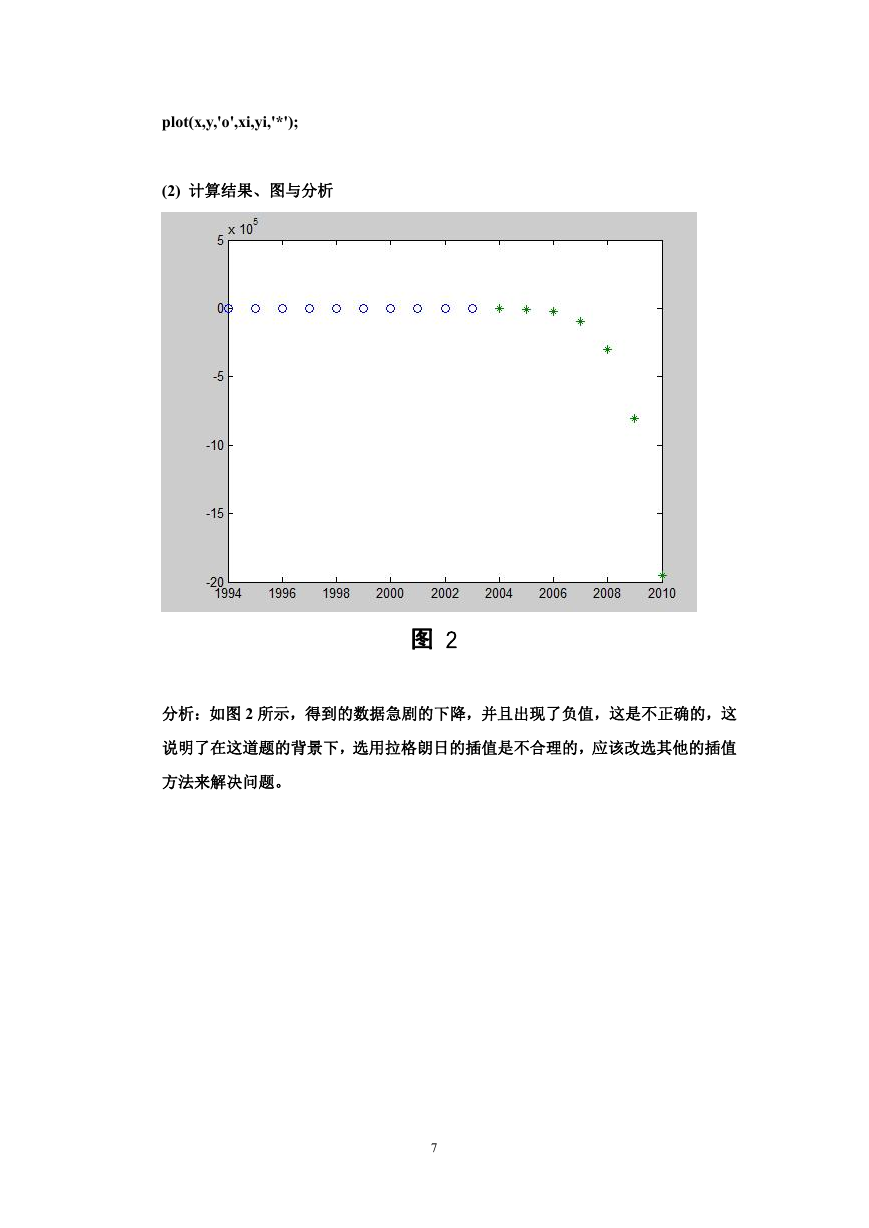
图 2
分析：如图 2 所示，得到的数据急剧的下降，并且出现了负值，这是不正确的，这
说明了在这道题的背景下，选用拉格朗日的插值是不合理的，应该改选其他的插值
方法来解决问题。
7
相关推荐
2023年江西萍乡中考道德与法治真题及答案.doc
2012年重庆南川中考生物真题及答案.doc
2013年江西师范大学地理学综合及文艺理论基础考研真题.doc
2020年四川甘孜小升初语文真题及答案I卷.doc
2020年注册岩土工程师专业基础考试真题及答案.doc
2023-2024学年福建省厦门市九年级上学期数学月考试题及答案.doc
2021-2022学年辽宁省沈阳市大东区九年级上学期语文期末试题及答案.doc
2022-2023学年北京东城区初三第一学期物理期末试卷及答案.doc
2018上半年江西教师资格初中地理学科知识与教学能力真题及答案.doc
2012年河北国家公务员申论考试真题及答案-省级.doc
2020-2021学年江苏省扬州市江都区邵樊片九年级上学期数学第一次质量检测试题及答案.doc
2022下半年黑龙江教师资格证中学综合素质真题及答案.doc
