logo资料库

SVM原理详解.docx

发布时间：2022-06-09 发布人：admin 分类：说明书 资料大小：0.32M 资料格式：docx 举报 版权申诉
第1页 / 共34页
第2页 / 共34页
第3页 / 共34页
第4页 / 共34页
第5页 / 共34页
第6页 / 共34页
第7页 / 共34页
第8页 / 共34页
资料共34页，剩余部分请下载后查看
    （一）SVM的八股简介
    SVM入门（二）线性分类器Part 1
    SVM入门（三）线性分类器Part 2
    （一）SVM 的八股简介 支持向量机(Support Vector Machine)是 Cortes 和 Vapnik 于 1995 年首先提出 的，它在解决小样本、非线性及高维模式识别中表现出许多特有的优势，并能够 推广应用到函数拟合等其他机器学习问题中[10]。 支持向量机方法是建立在统计学习理论的 VC 维理论和结构风险最小原理基础 上的，根据有限的样本信息在模型的复杂性（即对特定训练样本的学习精度， Accuracy）和学习能力（即无错误地识别任意 样本的能力）之间寻求最佳折衷， 以期获得最好的推广能力[14]（或称泛化能力）。 以上是经常被有关 SVM 的学术文献引用的介绍，有点八股，我来逐一分解并解 释一下。 Vapnik 是统计机器学习的大牛，这想必都不用说，他出版的《Statistical Learning Theory》是一本完整阐述统计机器学习思想的名著。在该书中详细的 论证了统计机器学习之所以区别于传统机器学习的本质，就在于统计机器学习能 够精确的 给出学习效果，能够解答需要的样本数等等一系列问题。与统计机器 学习的精密思维相比，传统的机器学习基本上属于摸着石头过河，用传统的机器 学习方法构造分 类系统完全成了一种技巧，一个人做的结果可能很好，另一个 人差不多的方法做出来却很差，缺乏指导和原则。 所谓 VC 维是对函数类的一种度量，可以简单的理解为问题的复杂程度，VC 维越 高，一个问题就越复杂。正是因为 SVM 关注的是 VC 维，后面我们可以看 到，SVM 解决问题的时候，和样本的维数是无关的（甚至样本是上万维的都可以，这使得 SVM 很适合用来解决文本分类的问题，当然，有这样的能力也因为引入 了核函 数）。 结构风险最小听上去文绉绉，其实说的也无非是下面这回事。 机器学习本质上就是一种对问题真实模型的逼近（我们选择一个我们认为比较好 的近似模型，这个近似模型就叫做一个假设），但毫无疑问，真实模型一定是 不 知道的（如果知道了，我们干吗还要机器学习？直接用真实模型解决问题不就可 以了？对吧，哈哈）既然真实模型不知道，那么我们选择的假设与问题真实解之 间 究竟有多大差距，我们就没法得知。比如说我们认为宇宙诞生于 150 亿年前 的一场大爆炸，这个假设能够描述很多我们观察到的现象，但它与真实的宇宙模 型之间 还相差多少？谁也说不清，因为我们压根就不知道真实的宇宙模型到底 是什么。 这个与问题真实解之间的误差，就叫做风险（更严格的说，误差的累积叫做风险）。 我们选择了一个假设之后（更直观点说，我们得到了一个分类器以后）， 真实 误差无从得知，但我们可以用某些可以掌握的量来逼近它。最直观的想法就是使 用分类器在样本数据上的分类的结果与真实结果（因为样本是已经标注过的数 据，是准确的数据）之间的差值来表示。这个差值叫做经验风险 Remp(w)。以前的 机器学习方法都把经验风险最小化作为努力的目 标，但后来发现很多分类函数 能够在样本集上轻易达到 100%的正确率，在真实分类时却一塌糊涂（即所谓的
    推广能力差，或泛化能力差）。此时的情况便是选择 了一个足够复杂的分类函 数（它的 VC 维很高），能够精确的记住每一个样本，但对样本之外的数据一律 分类错误。回头看看经验风险最小化原则我们就会发现，此 原则适用的大前提 是经验风险要确实能够逼近真实风险才行（行话叫一致），但实际上能逼近么？ 答案是不能，因为样本数相对于现实世界要分类的文本数来说简直 九牛一毛， 经验风险最小化原则只在这占很小比例的样本上做到没有误差，当然不能保证在 更大比例的真实文本上也没有误差。 统计学习因此而引入了泛化误差界的概念，就是指真实风险应该由两部分内容刻 画，一是经验风险，代表了分类器在给定样本上的误差；二是置信风险，代表 了 我们在多大程度上可以信任分类器在未知文本上分类的结果。很显然，第二部分 是没有办法精确计算的，因此只能给出一个估计的区间，也使得整个误差只能计 算 上界，而无法计算准确的值（所以叫做泛化误差界，而不叫泛化误差）。 置信风险与两个量有关，一是样本数量，显然给定的样本数量越大，我们的学习 结果越有可能正确，此时置信风险越小；二是分类函数的 VC 维，显然 VC 维越大， 推广能力越差，置信风险会变大。 泛化误差界的公式为： R(w)≤Remp(w)+Ф(n/h) 公式中 R(w)就是真实风险，Remp(w)就是经验风险，Ф(n/h)就是置信风险。统计 学习的目标从经验风险最小化变为了寻求经验风险与置信风险的和最小，即结构 风险最小。 SVM 正是这样一种努力最小化结构风险的算法。 SVM 其他的特点就比较容易理解了。 小样本，并不是说样本的绝对数量少（实际上，对任何算法来说，更多的样本几 乎总是能带来更好的效果），而是说与问题的复杂度比起来，SVM 算法要求的样 本数是相对比较少的。 非线性，是指 SVM 擅长应付样本数据线性不可分的情况，主要通过松弛变量（也 有人叫惩罚变量）和核函数技术来实现，这一部分是 SVM 的精髓，以后会 详细 讨论。多说一句，关于文本分类这个问题究竟是不是线性可分的，尚没有定论， 因此不能简单的认为它是线性可分的而作简化处理，在水落石出之前，只好先当 它是线性不可分的（反正线性可分也不过是线性不可分的一种特例而已，我们向 来不怕方法过于通用）。 高维模式识别是指样本维数很高，例如文本的向量表示，如果没有经过另一系列 文章（《文本分类入门》）中提到过的降维处理，出现几万维的情况很正常， 其 他算法基本就没有能力应付了，SVM 却可以，主要是因为 SVM 产生的分类器很简 洁，用到的样本信息很少（仅仅用到那些称之为“支持向量”的样本，此为后话），
    使得即使样本维数很高，也不会给存储和计算带来大麻烦（相 对照而言，kNN 算法在分类时就要用到所有样本，样本数巨大，每个样本维数再一高，这日子就 没法过了……）。 下一节开始正式讨论 SVM。别嫌我说得太详细哦。 SVM 入门（二）线性分类器 Part 1 线性分类器(一定意义上,也可以叫做感知机) 是最简单也很有效的分类器形式. 在一个线性分类器中,可以看到 SVM 形成的思路,并接触很多 SVM 的核心概念. 用一个二维空间里仅有两类样本的分类问题来举个小例子。如图所示 C1 和 C2 是要区分的两个类别，在二维平面中它们的样本如上图所示。中间的直线 就是一个分类函数，它可以将两类样本完全分开。一般的，如果一个线性函数能 够将样本完全正确的分开，就称这些数据是线性可分的，否则称为非线性可分的。 什么叫线性函数呢？在一维空间里就是一个点，在二维空间里就是一条直线，三 维空间里就是一个平面，可以如此想象下去，如果不关注空间的维数，这种线性 函数还有一个统一的名称——超平面（Hyper Plane）！ 实际上，一个线性函数是一个实值函数（即函数的值是连续的实数），而我们的 分类问题（例如这里的二元分类问题——回答一个样本属于还是不属于一个类别 的问题）需要离散的输出值，例如用 1 表示某个样本属于类别 C1，而用 0 表示不 属于（不属于 C1 也就意味着属于 C2），这时候只需要简单的在实值函数的基础 上附加一个阈值即可，通过分类函数执行时得到的值大于还是小于这个阈值来确 定类别归属。 例如我们有一个线性函数 g(x)=wx+b 我们可以取阈值为 0，这样当有一个样本 xi 需要判别的时候，我们就看 g(xi)的 值。若 g(xi)>0，就判别为类别 C1，若 g(xi)<0，则判别为类别 C2（等于的时候我
    们就拒绝判断，呵呵）。此时也等价于给函数 g(x)附加一个符号函数 sgn()，即 f(x)=sgn [g(x)]是我们真正的判别函数。 关于 g(x)=wx+b 这个表达式要注意三点：一，式中的 x 不是二维坐标系中的横轴， 而是样本的向量表示，例如一个样本点的坐标是(3,8)，则 xT=(3,8) ，而不是 x=3（一般说向量都是说列向量，因此以行向量形式来表示时，就加上转置）。 二，这个形式并不局限于二维的情况，在 n 维空间中仍然可以使用这个表 达式， 只是式中的 w 成为了 n 维向量（在二维的这个例子中，w 是二维向量，为了表示 起来方便简洁，以下均不区别列向量和它的转置，聪明的读者一看便知）； 三， g(x)不是中间那条直线的表达式，中间那条直线的表达式是 g(x)=0，即 wx+b=0， 我们也把这个函数叫做分类面。 实际上很容易看出来，中间那条分界线并不是唯一的，我们把它稍微旋转一下， 只要不把两类数据分错，仍然可以达到上面说的效果，稍微平移一下，也可 以。 此时就牵涉到一个问题，对同一个问题存在多个分类函数的时候，哪一个函数更 好呢？显然必须要先找一个指标来量化“好”的程度，通常使用的都是叫做“分 类间隔”的指标。下一节我们就仔细说说分类间隔，也补一补相关的数学知识。 SVM 入门（三）线性分类器 Part 2 上回说到对于文本分类这样的不适定问题（有一个以上解的问题称为不适定问 题），需要有一个指标来衡量解决方案（即我们通过训练建立的分类模型）的好 坏，而分类间隔是一个比较好的指标。 在进行文本分类的时候，我们可以让计算机这样来看待我们提供给它的训练样本， 每一个样本由一个向量（就是那些文本特征所组成的向量）和一个标记（标示出 这个样本属于哪个类别）组成。如下： Di=(xi,yi) xi 就是文本向量（维数很高），yi 就是分类标记。 在二元的线性分类中，这个表示分类的标记只有两个值，1 和-1（用来表示属于 还是不属于这个类）。有了这种表示法，我们就可以定义一个样本点到某个超平 面的间隔： δi=yi(wxi+b) 这个公式乍一看没什么神秘的，也说不出什么道理，只是个定义而已，但我们做 做变换，就能看出一些有意思的东西。 首先注意到如果某个样本属于该类别的话，那么 wxi+b>0（记得么？这是因为我 们所选的 g(x)=wx+b 就通过大于 0 还是小于 0 来判断分类），而 yi 也大于 0；若 不属于该类别的话，那么 wxi+b<0，而 yi 也小于 0，这意味着 yi(wxi+b)总是大于 0 的，而且它的值就等于|wxi+b|！（也就是|g(xi)|）
    现在把 w 和 b 进行一下归一化，即用 w/||w||和 b/||w||分别代替原来的 w 和 b， 那么间隔就可以写成 这个公式是不是看上去有点眼熟？没错，这不就是解析几何中点 xi到直线 g(x)=0 的距离公式嘛！（推广一下，是到超平面 g(x)=0 的距离， g(x)=0 就是上节中 提到的分类超平面） 小 Tips：||w||是什么符号？||w||叫做向量 w 的范数，范数是对向量长度的一 种度量。我们常说的向量长度其实指的是它的 2-范数，范数最一般的表示形式 为 p-范数，可以写成如下表达式 向量 w=(w1, w2, w3,…… wn) 它的 p-范数为 看看把 p 换成 2 的时候，不就是传统的向量长度么？当我们不指明 p 的时候，就 像||w||这样使用时，就意味着我们不关心 p 的值，用几范数都可以；或者上文 已经提到了 p 的值，为了叙述方便不再重复指明。 当用归一化的 w 和 b 代替原值之后的间隔有一个专门的名称，叫做几何间隔，几 何间隔所表示的正是点到超平面的欧氏距离，我们下面就简称几何间隔为“距 离”。以上是单个点到某个超平面的距离（就是间隔，后面不再区别这两个词） 定义，同样可以定义一个点的集合（就是一组样本）到某个超平面的距离为此集 合中 离超平面最近的点的距离。下面这张图更加直观的展示出了几何间隔的现 实含义：
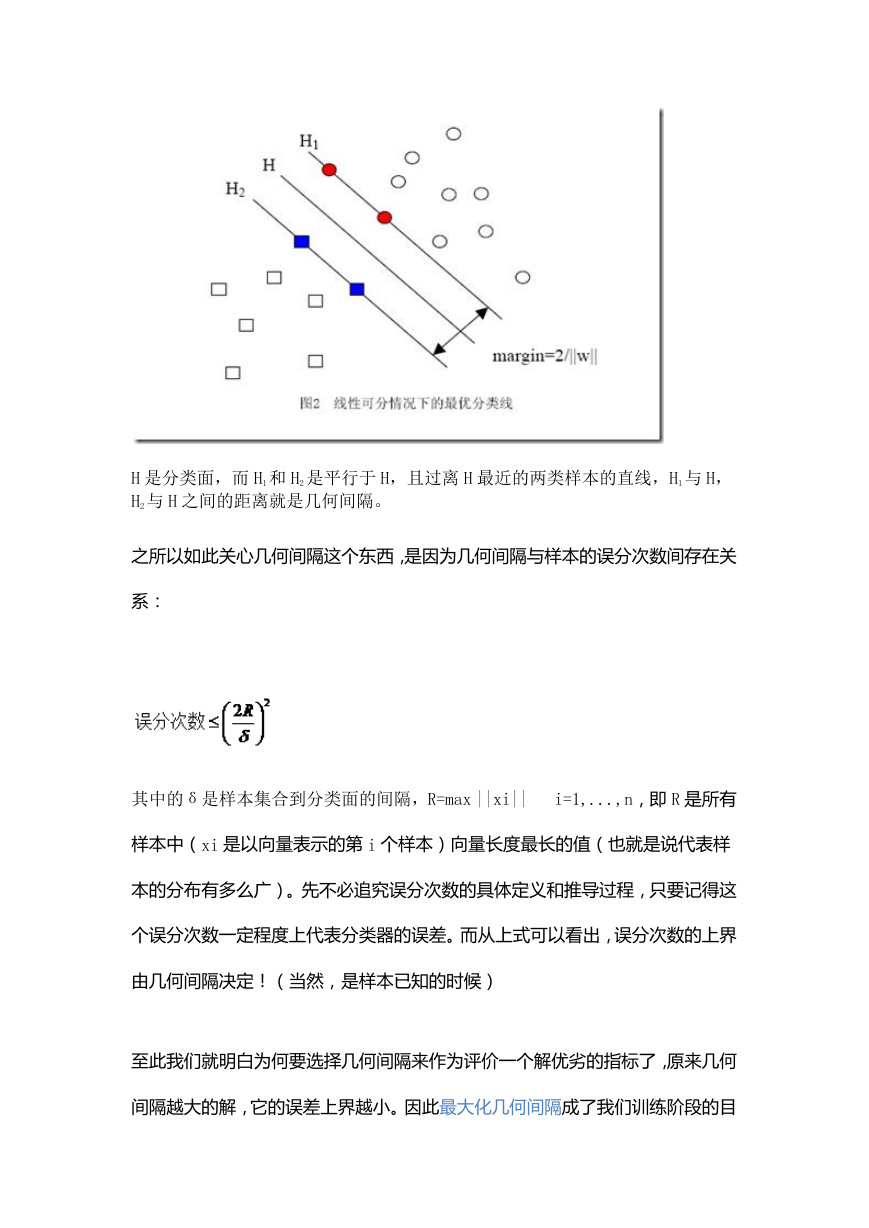
    H 是分类面，而 H1 和 H2 是平行于 H，且过离 H 最近的两类样本的直线，H1 与 H， H2 与 H 之间的距离就是几何间隔。 之所以如此关心几何间隔这个东西，是因为几何间隔与样本的误分次数间存在关 系： 其中的δ是样本集合到分类面的间隔，R=max ||xi|| i=1,...,n，即 R 是所有 样本中（xi 是以向量表示的第 i 个样本）向量长度最长的值（也就是说代表样 本的分布有多么广）。先不必追究误分次数的具体定义和推导过程，只要记得这 个误分次数一定程度上代表分类器的误差。而从上式可以看出，误分次数的上界 由几何间隔决定！（当然，是样本已知的时候） 至此我们就明白为何要选择几何间隔来作为评价一个解优劣的指标了，原来几何 间隔越大的解，它的误差上界越小。因此最大化几何间隔成了我们训练阶段的目
    标，而且，与二把刀作者所写的不同，最大化分类间隔并不是 SVM 的专利，而是 早在线性分类时期就已有的思想。 SVM 入门（四）线性分类器的求解——问题 的描述 Part1 上节说到我们有了一个线性分类函数，也有了判断解优劣的标准——即有了优化 的目标，这个目标就是最大化几何间隔，但是看过一些关于 SVM 的论文的人一定 记得什么优化的目标是要最小化||w||这样的说法，这是怎么回事呢？回头再看 看我们对间隔和几何间隔的定义： 间隔：δ=y(wx+b)=|g(x)| 几何间隔： 可以看出δ=||w||δ几何。注意到几何间隔与||w||是成反比的，因此最大化几何 间隔与最小化||w||完全是一回事。而我们常用的方法并不是固定||w||的大小而 寻求最大几何间隔，而是固定间隔（例如固定为 1），寻找最小的||w||。 而凡是求一个函数的最小值（或最大值）的问题都可以称为寻优问题（也叫作一 个规划问题），又由于找最大值的问题总可以通过加一个负号变为找最小值的问 题，因此我们下面讨论的时候都针对找最小值的过程来进行。一个寻优问题最重 要的部分是目标函数，顾名思义，就是指寻优的目标。例如我们想寻找最小的 ||w||这件事，就可以用下面的式子表示： 但实际上对于这个目标，我们常常使用另一个完全等价的目标函数来代替，那就 是： (式 1)
    不难看出当||w||2 达到最小时，||w||也达到最小，反之亦然（前提当然是||w|| 描述的是向量的长度，因而是非负 的）。之所以采用这种形式，是因为后面的 求解过程会对目标函数作一系列变换，而式（1）的形式会使变换后的形式更为 简洁（正如聪明的读者所料，添加的系数 二分之一和平方，皆是为求导数所需）。 接下来我们自然会问的就是，这个式子是否就描述了我们的问题呢？（回想一下， 我们的问题是有一堆点，可以被分成两类，我们要找出最好的分类面） 如果直接来解这个求最小值问题，很容易看出当||w||=0 的时候就得到了目标函 数的最小值。但是你也会发现，无论你给什么样的数据，都是这个解！ 反映在 图中，就是 H1 与 H2 两条直线间的距离无限大，这个时候，所有的样本点（无论 正样本还是负样本）都跑到了 H1 和 H2 中间，而我们原本的意图是，H1 右侧的 被分为正类，H2 左侧的被分为负类，位于两类中间的样本则拒绝分类（拒绝分 类的另一种理解是分给哪一类都有道理，因而分给哪一类也都没有道理）。这下 可好，所有样本点都进 入了无法分类的灰色地带。 造成这种结果的原因是在描述问题的时候只考虑了目标，而没有加入约束条件， 约束条件就是在求解过程中必须满足的条件，体现在我们的问题中就是样本点必 须在 H1 或 H2 的某一侧（或者至少在 H1 和 H2 上），而不能跑到两者中间。我们 前文提到过把间隔固定为 1，这是指把所有样本点中间隔最小的那一点的间隔定 为 1（这也是集合的间隔的定义，有点绕嘴），也就意味着集合中的其他点间隔 都不 会小于 1，按照间隔的定义，满足这些条件就相当于让下面的式子总是成 立： yi[(w·xi)+b]≥1 (i=1,2,…,l) （l 是总的样本数） 但我们常常习惯让式子的值和 0 比较，因而经常用变换过的形式：
    分享到：
    赞 收藏

    相关推荐

    资料库

    课程资源

    共收录17145份资料，累计13个分类，关注成员有19位，主要包括：PHP,网络管理,网页制作,Java,.Net,数据库,3G/移动开发,C/C++,游戏开发,嵌入式,讲义,软件测试,专业指导

    热门标签

    PHP 网络管理 网页制作 Java .Net 数据库 3G/移动开发 C/C++ 游戏开发 嵌入式 讲义 软件测试 专业指导

    最新资料