小波分析在信号特征提取中的应用.pdf-资料库

shipinchuang1-3169231-16359647375806723801.pdf-第1页.png

第1页 / 共34页

shipinchuang1-3169231-16359647375806723801.pdf-第2页.png

第2页 / 共34页

shipinchuang1-3169231-16359647375806723801.pdf-第3页.png

第3页 / 共34页

shipinchuang1-3169231-16359647375806723801.pdf-第4页.png

第4页 / 共34页

shipinchuang1-3169231-16359647375806723801.pdf-第5页.png

第5页 / 共34页

shipinchuang1-3169231-16359647375806723801.pdf-第6页.png

第6页 / 共34页

shipinchuang1-3169231-16359647375806723801.pdf-第7页.png

第7页 / 共34页

shipinchuang1-3169231-16359647375806723801.pdf-第8页.png

第8页 / 共34页

小波分析在信号特征提取中的应用内容摘要：小波分析是目前国际上公认的最新时间—频率分析工具，由于其“自适应性”和“数学显微镜性质”而成为许多学科的共同关注的焦点，对于信号处理、信息处理起着至关重要的作用。本文简要介绍了小波变换的基本理论，并结合数字调制信号和小波函数的有关理论知识，列举了小波分析在信号特征提取领域的方法和应用实例，进一步说明了小波变换在这些领域的理论意义和应用价值。索引关键词小波变换小波分析信号处理信号特征提取 I

Abstract Wavelet analysis is internationally recognized up to the minute tools for analyzing time-frequency. It is chiefly due to the “adaptive feature” and “mathematical microtelescope feature”,wavelet analysis is becoming a focus point of many sciences. It palys an important role in the signal & information processing. This paper briefly introduced the basic theory of wavelet transform, the parallel connection gathers the Digital modulate signal and the Wavelet function related theory knowledge, has enumerated the wavelet analysis in the extracted of signal feature domain methods and application examples, further explained the wavelet transform in these domains theory significances and the application value. Key Words: Wavelet transform Wavelet Analysis signal processing extracted of signal feature II

目录第一章绪论 ................................................................................... - 1 - 1.1 课题背景和意义 ........................................................................ - 1 - 1.2 论文的内容及安排 .................................................................... - 2 - 第二章小波变换的基本理论 ....................................................... - 3 - 2.1 连续小波变换 ............................................................................ - 3 - 2.2 离散小波变换 ............................................................................ - 5 - 2.3 小波包分析 ................................................................................... - 9 - 2.4 几种常用小波函数 .................................................................. - 11 - 第三章信号特征提取理论 ............................................................. - 13 - 3.1 信号特征提取的处理方法 ....................................................... - 13 - 3.2 小波变换用于表征信号的突变特征 ...................................... - 16 - 3.3 信号调制参数的提取 .............................................................. - 18 - 3.4 信号特征提取实例 .................................................................. - 22 - 第四章结语 ................................................................................... - 30 - 后记 ...................................................................... 错误!未定义书签。参考文献 ........................................................................................... - 31 - III

第一章绪论 1.1 课题背景和意义小波变换是 80 年代后期发展起来的应用数学分支，最早是由法国地球物理学家 Morlet 于 20 世纪 80 年代初在分析地球物理信号时作为一种信号分析的数学工具提出来的。而在将小波理论引入工程应用，特别是信号处理领域，法国学者 I. Daubechies 和 S. Mallet 起了极为重要的作用。在信号截获分析中，信号特征的提取十分重要，它是信号调制识别的基础，信号特征提取的好坏关系识别的效果，因此，信号特征提取对信号的分析具有重要意义。但是传统的平稳分析方法不能完全满足要求，因而一般使用非平稳信号分析的方法完成。传统的信号分析是建立在傅立叶（Fourier）变换的基础上的，由于傅立叶分析使用的是一种全局变换，要么完全在时域，要么完全在频域，因此无法表述信号的时频局域性质，而这种性质恰恰是非平稳信号最根本和最关键的性质。为了处理和分析非平稳信号，人们提出并发展了一系列新的信号分析理论：短时傅立叶变换、 Gabor 变换、时频分析、小波变换、Randon -Wigner 变换、分数阶傅立叶变换理论等。小波变换是时频分析的另一种方法，是近年来发展起来的一个崭新数学工具，它是一种时间—尺度分析法，尺度与频率相对应，因此它是一种时频分析法。小波分析在时域和频域都有表征信号局部特征的能力，在低频部分具有较高的频域分辨率和较低的时间分辨率，而在高频部分具有较高的时间分辨率和较低的频率分辨率，信号分析中的这种多分辨的观点是小波变换的基本点。在小波理论的发展过程中，发现它与工程技术上一些已经发展起来的问题密切相关。它们都可以用小波作为理论基础，看成是不同角度应用小波所得的特例。例如Gabor在 1946 年提出的Gabor变换，Burt在 1982 年提出的金字塔式图像压缩编码概念，通信及语音处理中的子带编码（subband coding），计算机视觉中的多分辨分析 - 1 -

等。这些工程应用领域大大丰富了小波变换的实际意义，也促进了小波分析理论的进一步发展。小波理论已由一维发展到多维。二维的情况下它除了“显微”能力以外还具有“极化”能力（即方向选择性）。M. V. Wickerhauser等人提出的“小波包”（wavelet packet）更进一步发展了小波理论。目前小波变换在语音、图像、通信、雷达、水声、地震、生物医学等领域都有应用，是信号处理的前沿课题，并且成为多学科关注的热点。 1.2 论文的内容及安排本文对小波变换的基本理论和信号特征提取理论进行了介绍，小波变换方法应用于信号分析，主要进行了信号的多分辨率分析，信号特征提取的方法和应用，具体安排如下: 1、第一章是绪论，介绍了研究的背景及意义。 2、第二章对小波变换基本理进行了阐述。从连续小波变换和离散小波变换分析入手，反映出小波变换具有多分辨率的特性。其中重点阐述了离散小波变换的快速算法—Mallat算法。最后简要介绍了小波包分析和几种常用的小波函数。 3、第三章简单介绍了信号特征提取理论，作为数字调制信号的瞬时特征提取的理论来源。说明小波变换可以用于表征信号的突变特征，并且可以提取信号特征。阐述了信号特征提取的处理方法，并对数字调制信号瞬时特征和调制参数的提取进行了介绍。最后举例对信号特征提取进行了进一步的说明，并进行了仿真和分析。 - 2 -

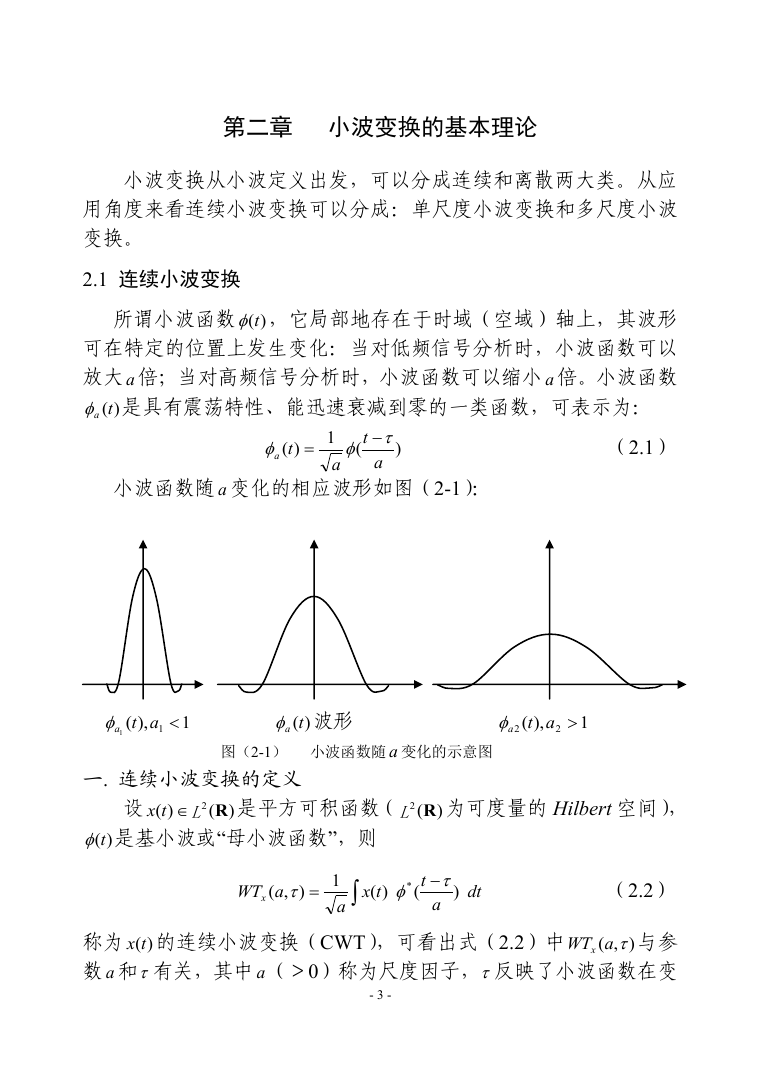
第二章小波变换的基本理论小波变换从小波定义出发，可以分成连续和离散两大类。从应用角度来看连续小波变换可以分成：单尺度小波变换和多尺度小波变换。 2.1 连续小波变换所谓小波函数，它局部地存在于时域（空域）轴上，其波形可在特定的位臵上发生变化：当对低频信号分析时，小波函数可以放大倍；当对高频信号分析时，小波函数可以缩小倍。小波函数是具有震荡特性、能迅速衰减到零的一类函数，可表示为：（2.1）小波函数随变化的相应波形如图（2-1）：波形图（2-1）小波函数随变化的示意图一. 连续小波变换的定义设是基小波或“母小波函数”，则是平方可积函数（为可度量的 Hilbert 空间），（2.2）称为的连续小波变换（CWT），可看出式（2.2）中与参数和有关，其中（＞0）称为尺度因子，反映了小波函数在变 - 3 - )(taa)(ta)(1)(atataa1),(11ata)(ta1),(22ataa)(tx)(2RL)(2RL)(tdtattxaaWTx)()(1),(*)(tx),(aWTxaa

换中的位移，且的容许条件下，小波变换的逆变换为：（即是带通滤波器）。在式（2.4）（2.3）其中 < （2.4）式（2.4）中，为的 Fourier 变换。若的 Fourier 变换为，则由 Fourier 变换的性质，可得：（2.5）变换也可表示为内积形式：（2.6）二. 连续小波变换的性质（1）小波变换是一个满足能量守恒方程的线形运算，它把一个信号分解成对空间和尺度（即时间和频率）的独立贡献，同时又不失原信号所包含的信息；（2）小波变换相当于一个具有放大、缩小和平移等功能的数学显微镜，通过检查不同放大倍数下信号的变化来研究其动态特性；（3）小波变换不一定要求是正交的，小波基不惟一。小波函数系的时宽-带宽积很小，且在时间和频率轴上都很集中，即展开系数的能量很集中；（4）小波变换巧妙地利用了非均匀的分辨率，较好地解决了时间和频率分辨率的矛盾；在低频段用高的频率分辨率和低的时间分辨率（宽的分析窗口），而在高频段则用低的频率分辨率和高的时间分辨率（窄的分析窗口），这与时变信号的特征一致；（5）小波变换将信号分解为在对数坐标中具有相同大小频带的集合，这种以非线形的对数方式而不是以线形方式处理频率的方法对时变信号具有明显的优越性；（6）小波变换是稳定的，是一个信号的冗余表示。由于 a、b 是连续变化的，相邻分析窗的绝大部分是相互重叠的，相关性很强；（7）小波变换同傅立叶变换一样，具有统一性和相似性，其正 - 4 - ()0tdt)(tdataaWTadactxx)(1),(1)(02dtc20)()()()(t)(tx)(XdeaXaaWTjx)()(2),(*)(),(),(ttxaWTax

反变换具有完美的对称性。小波变换具有基于卷积和 QMF 的塔形快速算法。 2.2 离散小波变换一. 离散小波变换的定义定义 2.1：设的标准正交基，则称函数为正交小波，，，若称为为正交小波基，称为小波子空间。间中的任意函数展开成级数形式。所以在小波分析中，当由内积空间理论可知，通过空间中的基函数的线性组合可把空为都可以用小波基展开成的规范正交基时，对于任意的小波级数：其中小波系数可通过和的内积来计算：（2.7）（2.8）从连续小波变换的讨论中我们可以看出，对一维信号作小波变换的结果为二维的，其信息是有冗余的。从节约计算和数据压缩的角度，一般采用离散尺度和位移来计算小波变换。通常小波变换中变换尺度是按照幂级数作离散化的：若令依次取 1,2,22,23,……，则对应的小波基函数为故而离散小波变换可表示为：。（2.9）逆变换为：（2.10）实际应用中，信号通常是离散的或者由采样得到，也就是说时间通常也是以离散的形式出现的。以幂级数对尺度和偏移进行离散是一种高效的离散化方法，因为指数的小的变化就会引起尺度的很大的变化。目前通行的方法是取，对尺度和偏移进行二进制离散，即 - 5 - )()(2RLt/2()()jjjktaatkZkjkj,,)(2RLZkjkj,,ZkjkjjtspanW,,)(Zkjkj,,)(2RL)(2RLxZkjkjkjdx,,,kjd,xkj,dkxxdkjRkjkj*,,,,)(tx),(aWTxa)2(2)(2/ktxjjjkdtttxkjWTjkx)()(),(*ZkjkjkZjtctx)()()(tftabja1,200baZkjkbajj,,2,2

资料库

小波分析在信号特征提取中的应用.pdf

相关推荐

课程资源

热门标签

最新资料