Λ Λ Λ 仪器与仪表 谭勋琼: 基于遗传算法的自适应神经模糊控制器 基于遗传算法的自适应神经模糊控制器 谭勋琼 (长沙理工大学 物理与电子科学系　湖南 长沙　410076) 摘　要: 分析了自适应神经模糊系统的特性, 以此设计一个智能控制器, 控制器的输入为误差和误差变化率, 输出为 控制量。 遗传算法是一种有效的全局最优搜索算法, 对于复杂、非线性的空间也能够快速地搜索最优解, 因而本文利用遗 传算法来优化自适应神经模糊控制器的参数。 仿真实验表明, 该方法优化得到的控制器具有优良的控制效果。 关键词: 自适应; 模糊神经系统; 遗传算法; 智能控制 中图分类号: T P312　　　　　文献标识码: B 　　　　　文章编号: 1004 373X (2005) 08 072 03 Self adaptive Neura l Fuzzy System Con troller Ba sed on Genetic A lgor ithm (D ep artm en t of Physics & E lectron ic Science, Changsha U n iversity of T echno logy, Changsha, 410076, Ch ina) TAN Xunqiong A bs tra c t: T he paper analyzes the characteristic of self the ou tpu t inpu t of con tro ller are erro r and rate of erro r, search ing algo rithm even fo r com p lex, non linear system s resu lts show the good perfo rm ance of th is con tro ller adap tive neu ral fuzzy system , and design s an in telligen t con tro ller is con tro l values Genetic A lgo rithm (GA ) T he is a k ind of u sefu l global Sim u lation In th is paper, w e app ly GA fo r the op tim ization of param eters Ke yw o rds: self adap tive; neu ral fuzzy system ; genetic algo rithm ; in telligen t con tro l 　　在现代工业生产工程实际中, 许多具体控制对象都是 非线性的, 其模型参数一般也不确定, 采用传统的控制方 法, 往往不能有效地控制各种工况、参数的实际对象。随着 模糊控制、专家控制、神经控制等智能控制理论方法的发展 和应用, 智能控制相对于传统控制在很多方面都具有优势, 因而得到了广泛的应用。自适应神经模糊系统, 充分结合了 模糊控制和神经网络的优点, 模糊逻辑不依赖于控制对象 的模型, 神经网络又具有极好的学习能力, 所设计的智能控 制器具有很好的控制效果。 一般而言, 神经网络的训练多采用BP 算法, 很容易陷 入局部最优解。遗传算法是一种优良的全局最优搜索方法, 对于复杂、非线性问题仍然具有很好的优化效果, 因此, 本 文在分析自适应神经模糊系统的基础上, 采用遗传算法来 优化网络系统参数。仿真实验表明了这种方法得到的控制 器具有优良的控制效果。 1　自适应神经模糊推理系统 (ANF IS) 结构 为简单起见, 假定所考虑的模糊推理系统有 2 个输入, 分别对应于控制中的误差 E 和误差变化率 EC。模糊逻辑控 制器是执行 T akagi Sugeno 推理的控制器。考虑控制器为 多输入单输出结构。控制规则有如下形式: 规则 1: 如果 E 是A 1 and EC 是B 1, 那么 f 1 = p 1E + q1EC + r1; 收稿日期: 2004 12 06 27 规则 2: 如果 E 是 A 2 and EC 是 B 2, 那么 f 2 = p 2E + q2EC + r2。 图 1　控制器网络结构 第 1 层: 每个节点 i 是一个有结点函数的自适应结点: O 1, i = A i (E ) 　　　　i = 1, 2 B i- 2i (EC ) 　　　　i = 3, 4 或者: 　 O 1, i = (1) 其中: E 和 EC 是结点 i 的输入; A 和B 是与该结点有关的语 言标识 (如“小”、“中”、“大”)。所以 O 1, i 是模糊集 A 的隶属 度。这里选取A 的隶属函数为: A (x ) = 1 + 1 x - a i 2b ci (2) 

1 《现代电子技术》2005 年第 8 期总第 199 期 　 电子元器件 　　第 2 层: 每个结点是一个标以 是所有输入信号的积: 的固定结点, 他的输出 遗传算法的流程如图 3 所示。 A i (E ) O 2, i = B i (EC ) 　　　　i = 1, 2 (3) 　　第 3 层: 每个结点是一个标以N 的固定结点。第 i 个结 点计算第 i 条规则的激励强度与所有规则的激励强度之和 的比值。为方便起见, 本层的输出称为归一化激励强度: O 3, i = = i 1 + 2 　　　　i = 1, 2 (4) 　　第 4 层: 每个结点 i 是一个有结点函数的自适应结点: (5) i 是从第 3 层传来的归一化激励强度; {p i, qi, r i} 是该 i (p iE + qiEC + ri) O 4, i = if i = 这里 结点的参数集。 第 5 层: 单结点是一个标以∑ 的固定结点, 计算所有 传来信号之和作为总输出: U = O 5, 1 = ∑ if i = ∑i ∑i if i i (6) 　　对于 25 条规则的AN F IS 结构, 每个输入对应于 5 个 相关的隶属函数。图 2 表示AN F IS 把二维输入空间划分为 25 个模糊区域。每一条 IF TH EN 规则对应于一个模糊区 域, 即每条规则的前提部分定义了一个模糊区域, 而结论部 分确定了该区域内的输出。 2 2　遗传算法优化的AN F IS 控制器 控制器结构如图 4 所示。 图 3 中性能指标为每次采样误差, 在线优化AN F IS 中 的 p i, qi, ri 参数。 图 3　遗传算法流程图 图 4　基于 GA 优化的AN F IS 控制器 GA 求解问题的步骤如下: 参数的编码　这里采用十进制编码方式, 种群中每一 个十进制的基因就代表AN F IS 网络中需要训练的参数, 即 p i, qi, r i 。 种群数目 N 的确定　种群数目应该取一个比较合适 的值, 一般在 30～ 150 之间, 种群数目太大, 每一代种群的 运算时间就长些; 种群数目太小, 迭代的次数会明显增加。 适应值计算　在 AN F IS 的优化中, 每一个个体的适 应度应该以其训练误差为参考, 取所有训练样本的整体误 差作为其适应度, 误差越大适应度越小, 误差越小适应度 越大。即用误差函数 E 来衡量适应度: fitness (P i) = E m ax - E P i 图 2　模糊区域分割图 式中: E m ax表示误差函数的最大值。 2　GA 的原理及基于遗传算法的 ANF IS 优化 GA 与传统的优化方法相比有许多优点, 他的基本思想 是基于D arw in 的生物进化论与M endel 的遗传学机理基础 上的随机、迭代、进化, 具有广泛实用性的搜索方法。GA 搜索结合了D arw in 适者生存和随机交换理论, 前者消除了 解中的不适应因素, 后者利用原有解中的已有知识, 从而有 力地加速了搜索过程。该算法在寻优过程中只使用评价函 数, 不要求目标函数的可微性, 其寻优过程是从解空间的随 机点集出发, 而不是从一点开始, 所以 GA 具有全局性、并 行性、快速性和鲁棒性。 2 1　遗传算法流程 GA 是一种随机搜索算法, 能在概率意义上收敛到全局 最优解, 其收敛过程带有突变式特点, 因此在收敛到一定程 度时, 通过交叉、变异算子产生更高适应性个体的概率显著 降低, 从而收敛速度受到制约。 选择　利用轮盘赌算法从种群中产生下一代, 适应值 高的个体遗传的机会大, 适应值低的个体遗传的机会较 小, 根据算法可以产生种群数目不变的下一代。 交叉、变异操作　交叉和变异是产生适应度值更高个 85, 变异概率 2。合适的交叉概率和变异概率既能产 体的关键步骤, 交叉概率一般取值 0 一般取值 0 生适应值更好的下一代, 又能提高搜索的速度。 01～ 0 3～ 0 终止条件　选用的终止条件为 N 代内最佳适应没有 明显提高。N 太大则收敛时间太长, N 太小则得到的结果 与最优值误差太大。 也可以选用确定的叠代次数作为终 止条件。 3　仿真研究 如图 5 所示, 实线为给定的正弦信号 5sin (t) , 星号 为控制器的实际跟踪轨迹, 可以看出, 基于遗传自适应神 经模糊控制器的正弦跟踪效果良好。 37 

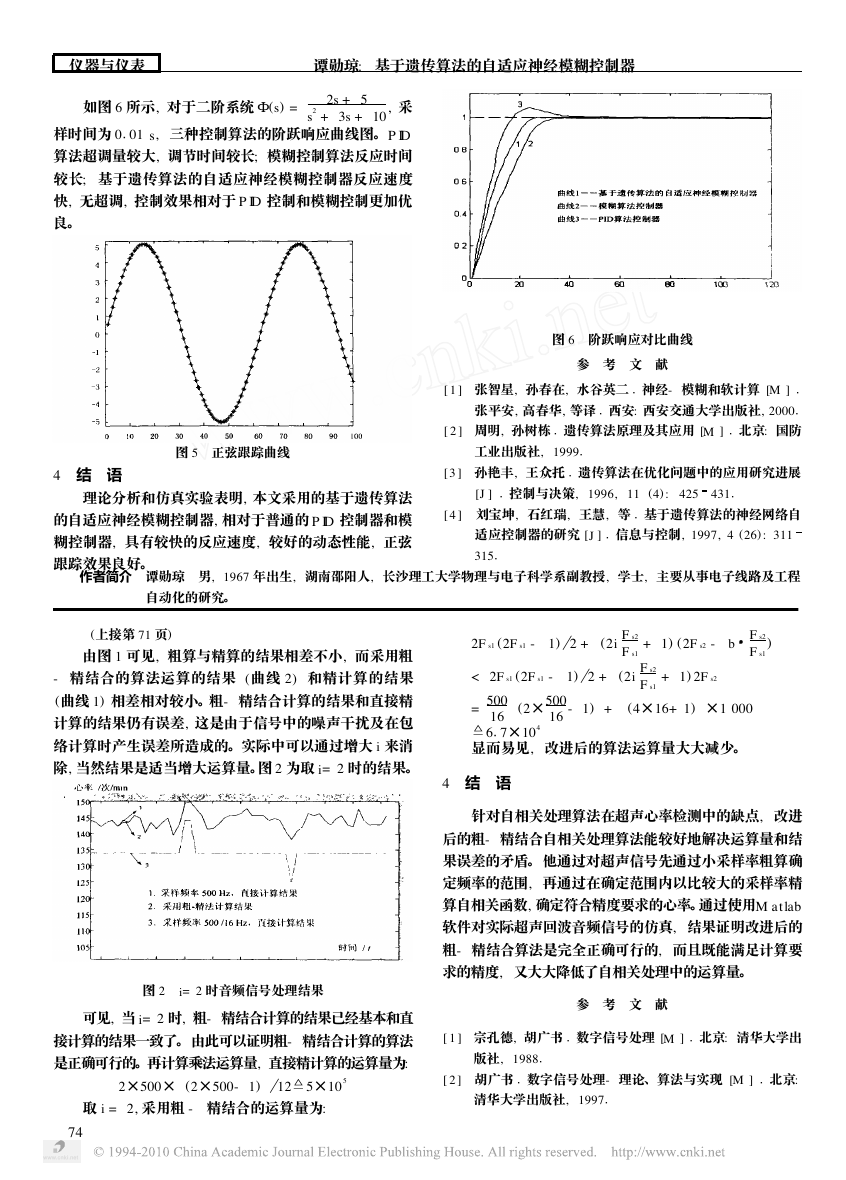
1 1 1 1 1 1 Ù ƒ 谭勋琼: 基于遗传算法的自适应神经模糊控制器 仪器与仪表 如图 6 所示, 对于二阶系统 (s) = 2s + 5 s2 + 3s + 10 , 采 01 s, 三种控制算法的阶跃响应曲线图。P ID 样时间为 0 算法超调量较大, 调节时间较长; 模糊控制算法反应时间 较长; 基于遗传算法的自适应神经模糊控制器反应速度 快, 无超调, 控制效果相对于 P ID 控制和模糊控制更加优 良。 图 6　阶跃响应对比曲线 参　考　文　献 [ 1 ] 张智星, 孙春在, 水谷英二 张平安, 高春华, 等译 神经- 模糊和软计算 [M ] 西安: 西安交通大学出版社, 2000 北京: 国防 遗传算法原理及其应用 [M ] [ 2 ] 周明, 孙树栋 图 5　正弦跟踪曲线 工业出版社, 1999 4　结　语 [3 ] 孙艳丰, 王众托 遗传算法在优化问题中的应用研究进展 理论分析和仿真实验表明, 本文采用的基于遗传算法 的自适应神经模糊控制器, 相对于普通的 P ID 控制器和模 糊控制器, 具有较快的反应速度, 较好的动态性能, 正弦 跟踪效果良好。 　　作者简介　谭勋琼　男, 1967 年出生, 湖南邵阳人, 长沙理工大学物理与电子科学系副教授, 学士, 主要从事电子线路及工程 适应控制器的研究 [J ] 315 [ 4 ] 刘宝坤, 石红瑞, 王慧, 等 信息与控制, 1997, 4 (26) : 311 基于遗传算法的神经网络自 [J ] 控制与决策, 1996, 11 (4) : 425 431 自动化的研究。 　　 (上接第 71 页) 由图 1 可见, 粗算与精算的结果相差不小, 而采用粗 - 精结合的算法运算的结果 (曲线 2) 和精计算的结果 (曲线 1) 相差相对较小。粗- 精结合计算的结果和直接精 计算的结果仍有误差, 这是由于信号中的噪声干扰及在包 络计算时产生误差所造成的。实际中可以通过增大 i 来消 除, 当然结果是适当增大运算量。图 2 为取 i= 2 时的结果。 图 2　i= 2 时音频信号处理结果 可见, 当 i= 2 时, 粗- 精结合计算的结果已经基本和直 接计算的结果一致了。由此可以证明粗- 精结合计算的算法 是正确可行的。再计算乘法运算量, 直接精计算的运算量为: 2×500× (2×500- 1) 12 5×10 5 取 i = 2, 采用粗 - 精结合的运算量为: 47 2F s1 (2F s1 - 1) 2 + (2i F s2 F s1 + 1) (2F s2 - b F s2 F s1 ) < 2F s1 (2F s1 - 1) (2×500 16 = 500 16 6 7×104 2 + (2i F s2 F s1 + 1) 2F s2 - 1) + (4×16+ 1) ×1 000 显而易见, 改进后的算法运算量大大减少。 4　结　语 针对自相关处理算法在超声心率检测中的缺点, 改进 后的粗- 精结合自相关处理算法能较好地解决运算量和结 果误差的矛盾。 他通过对超声信号先通过小采样率粗算确 定频率的范围, 再通过在确定范围内以比较大的采样率精 算自相关函数, 确定符合精度要求的心率。通过使用M atlab 软件对实际超声回波音频信号的仿真, 结果证明改进后的 粗- 精结合算法是完全正确可行的, 而且既能满足计算要 求的精度, 又大大降低了自相关处理中的运算量。 参　考　文　献 [ 1 ] 宗孔德, 胡广书 数字信号处理 [M ] 北京: 清华大学出 版社, 1988 [ 2 ] 胡广书 数字信号处理- 理论、算法与实现 [M ] 北京: 清华大学出版社, 1997