论文研究-求解TSP问题的自适应离散型布谷鸟算法.pdf

发布时间：2022-05-30 发布人：admin 分类：说明书资料大小：0.75M 资料格式：pdf 举报版权申诉

weixin_38744270-11697881-16359647282979020576.pdf-第1页.png

第1页 / 共7页

weixin_38744270-11697881-16359647282979020576.pdf-第2页.png

第2页 / 共7页

weixin_38744270-11697881-16359647282979020576.pdf-第3页.png

第3页 / 共7页

weixin_38744270-11697881-16359647282979020576.pdf-第4页.png

第4页 / 共7页

weixin_38744270-11697881-16359647282979020576.pdf-第5页.png

第5页 / 共7页

weixin_38744270-11697881-16359647282979020576.pdf-第6页.png

第6页 / 共7页

weixin_38744270-11697881-16359647282979020576.pdf-第7页.png

第7页 / 共7页

文本预览

48 2017，53（10） Computer Engineering and Applications 计算机工程与应用求解 TSP 问题的自适应离散型布谷鸟算法张子成，韩伟 ZHANG Zicheng, HAN Wei 南京财经大学信息工程学院，南京 210046 College of Information ＆ Engineering, Nanjing University of Finance and Economics, Nanjing 210046, China ZHANG Zicheng, HAN Wei. Adaptive discrete cuckoo algorithm for solving TSP problem. Computer Engineering and Applications, 2017, 53（10）：48-54. Abstract：For solving the TSP problem, this paper proposes an adaptive discrete cuckoo algorithm. Constructing path solution strategy of TSP problem based on the principle of cuckoo search algorithm. For the two defects of the discrete algorithm, one is overall adjustment can easily destroy the optimum path which is already formed, the other is the decline of diversity of population with the increase of the iteration number of the algorithm, this paper designs an adaptive partial adjustment operator and a global random perturbation strategy for path. In order to speed up the convergence rate of the algorithm, a simple 2-opt optimization operator is used as a local optimization operator. In the end, multiple sets of different sizes of standard TSPLIB data are compared with other optimization algorithms, the experimental result shows that the ADCS algorithm has advantages in solving precision and stability. Key words：TSP problem; cuckoo search algorithm; 2-opt optimization; partial adjustment; global random disturbance 摘要：对于求解的 TSP 问题，提出了一种自适应离散型布谷鸟算法（Adaptive Discrete Cuckoo Search，ADCS）。在基于布谷鸟搜索算法（Cuckoo Search，CS）的搜索原理下构造 TSP 问题的路径求解策略。针对离散型算法整体调整容易破坏已形成的较优路径和随着算法迭代数目增加导致种群多样性下降这两个缺陷，设计了一种针对路径的自适应型局部调整算子和全局随机扰动策略，采用了简单的 2-opt 优化算子作为局部优化算子以加快算法的收敛速度。最后采用多组不同规模的标准 TSPLIB 数据与其他的优化算法进行对比实验，结果表明 ADCS 算法在求解精度和稳定性方面具有优势。关键词：TSP 问题；布谷鸟搜索算法；2-opt 优化；局部调整；全局随机扰动文献标志码：A 中图分类号：TP18 doi：10.3778/j.issn.1002-8331.1512-0115 1 引言旅行商问题（Traveling Salesman Problem，TSP）[1]是经典的 NP 问题，其易于描述但是难以求解。旅行商问题可以描述为：一个旅行商要去若干个城市推销商品，该旅行商从一个初始城市出发经过所有城市后回到出发地，该旅行商应该如何选择环游路径使得环游距离最短。 TSP 问题具有重要的实际意义，其最初是用于优化交通运输路线，如物流配送、车辆路径等。随着学科的交叉性不断增强，TSP 问题也广泛运用于电子学科领域，如印制电路钻孔、路由分布等。印制电路板钻孔是 TSP 问题在电子学科的典型应用之一，在一块电路板上需要钻成千上百个孔，钻头在孔之间的移动就相当于环游所有的孔。可将印制电路板钻孔建模为 TSP 问题，下孔位置为城市位置，孔与孔之间的移动时间为城市间距离，钻孔耗时优化可以转化为 TSP 问题的优化。求解 TSP 问题的确定性算法，如分枝界定法（Branch and Bound Method， LC）[2]和动态规划算法（Dynamic Programming，DM）[3]，其复杂度呈指数增长，它们虽可以准确地找出 TSP 问题的最优解，但是随着 TSP 问题的城市规模变大，这些算法完全失效。近几十年来，国内外的专家学者受仿真学基金项目：国家电子商务信息处理国际联合研究中心项目（No.2013B01035）。作者简介：张子成（1991—），男，硕士研究生，研究领域为智能搜索、人工智能，E-mail：269627853@qq.com；韩伟（1975—），男，博士，副教授，研究领域为人工智能，电子商务，运筹学。收稿日期：2015-12-08 修回日期：2016-01-29 文章编号：1002-8331（2017）10-0048-07 CNKI 网络优先出版：2016-03-02, http://www.cnki.net/kcms/detail/11.2127.TP.20160302.1657.042.html

张子成，韩伟：求解 TSP 问题的自适应离散型布谷鸟算法 2017，53（10） 49 机理的启示，提出了一系列智能优化算法，如遗传算法（Genetic Algorithm，GA）[4]、模拟退火算法（Simulated Annealing，SA）[5]、蚁群算法（Ant Colony Optimization， ACO）[6]等。随着智能优化算法的不断发展，近年来许多新型的群体智能优化算法涌现而出，如布谷鸟搜索算法（Cuckoo Search，CS）[7]、萤火虫优化算法（Glowworm Swarm Optimization，GSO）[8]、粒子群优化算法[9]等。这些群智能优化算法已被广泛运用于求解 TSP 问题：杜鹏桢[10]等应用蚁群算法求解 TSP 问题，其先用 k-means 算法将城市分类，并针对不同类型的城市设计面向城市类型的蚂蚁，提高了蚁群的搜索能力。蚁群算法虽很适合求解 TSP 问题，但算法需要经过大次数的迭代后才能确定最优路径[11]；Yong Wang[12]提出了一种求解 TSP 问题的混合型遗传算法，即用遗传算法作为全局寻优策略，将所得路径用两种不同的局部优化算子进行局部优化。由于引入了局部优化算子，在城市规模较小时，该算法采用交叉的方式产生新的路径会很大程度上继承较优的父母路径，但在城市规模较大时，应用交叉算子产生的新路径很可能与较优的父母路径大不相同，这将导致算法对小规模算例精度较高，对于大规模城市精度下降较快；周永权[13]等将萤火虫算法运用于求解 TSP 问题，其基于萤火虫算法原理设计可行的交叉算子，修复不可行解，再运用 2-opt 优化算子进行局部优化，其对小规模的 TSP 问题求解精度较高，但其交叉算子随机性较大，易破坏已形成的较优路径，导致收敛速度下降，并且萤火虫算法参数较多，如若参数设置稍有不当，便会对搜索精度产生影响。布谷鸟搜索算法具有参数少易于调控、收敛速度快、全局寻优能力强等优点，其在连续函数优化的问题上展现出良好的性能[7]。近年来，布谷鸟搜索算法也成功应用于各类组合优化问题。Aziz Ouaarab[14]等应用布谷鸟算法求解 TSP 问题，其基于布谷鸟算法搜索原理，设计离散型问题的步长移动公式，但其使用的 2-opt 算子和 double-bridge 均为局部优化算子，在中小规模的问题上求解精度很高，但是问题规模变大后容易陷入局部最优。由于 2-opt 优化算子是一种收敛速度较快的优化算子，若用 2-opt 优化算子优化一条所得路径后再用变异、交叉等算子产生新路径的话会很有可能使得已形成的较优路径遭受破坏，所以设计了一种适合与 2-opt 优化算子相结合的自适应型局部调整算子。为了保持种群的多样性，使算法避免陷入局部最优，在路径上加入全局的随机扰动策略。 2 布谷鸟搜索算法和 2-opt 优化算子 2.1 布谷鸟搜索算法布谷鸟搜索算法（CS）是 Yang[7]于 2009 年提出的一种新型的智能优化算法。CS 模拟大杜鹃寄生育雏的习性，可有效求解最优化问题。CS 结构简单，参数较少，有着较强的跳出局部最优的能力。在布谷鸟算法中使用三个理想化的规则：（1）每个布谷鸟每次只产一个卵，并随机选择一个寄生窝用来孵化它。（2）在随机产生的寄生窝中，最好的寄生窝将会被保留到下一代。（3）可用的寄生窝的数量是一定的，寄生窝的主人发现外来鸟蛋的概率为 Pa 。在这三个理想化规则的基础下布谷鸟寻窝的路径和位置更新如下： X (t + 1) = X (t) i i + T⊕Levy( )λ （1）其中 T > 0 ，为步长大小，⊕ 表示为点对点乘法，Levy( )λ 为搜索路径，服从莱维分布[15-16]。算法伪代码[7]如下： Begin Objective function f (x) ，X =(x1,x2,⋯,xd) ，d 是问题的维数初始化 n 个鸟窝 Xi(i = 1,2,⋯,n) while (t < MaxGeneration) or (stop criterion) 采用莱维飞行随机生成新的解 f (xi) 在 n(say,j) 中随机选取一个鸟窝 if f (xi)> f (xj) 用新解替换鸟窝 j end 按发现概率 pa 丢弃差的解用偏好随机游动产生新的解替代丢弃的解保留最好的解，完成一次迭代 endwhile 最后处理结果与可视化显示 2.2 end 2-opt 优化算子 2-opt 优化算法[17]是一种用于 TSP 问题的简单可行的路径局部优化算法，它从城市的一个随机排列（称为路径 T ）开始并试图去改善它。 T 的邻域定义为交换 T 中不相邻的两条边得到的所有路径的集合。2-opt 的算法可以很容易地推广到 k-最优算法，但是随着 k 的增长算法搜索效率会大幅下降。所以 k>3 的 k-opt 算法的使用频率很低。从图 1 中可以看出如果 2-交换足够充分的话，则可以使路径中无交叉边。如图 1 所示。图 1 应用 2-opt 优化前后的路径图

50 2017，53（10） Computer Engineering and Applications 计算机工程与应用 3 求解 TSP 问题的自适应离散型布谷鸟算法在第 2 章中介绍的布谷鸟搜索算法是解决连续函数问题。TSP 为组合优化问题，所以要将连续型布谷鸟优化算法转化为离散型布谷鸟优化算法。首先将 TSP 问题的解进行编码，将每个解看成是一个鸟窝并初始化 N 个鸟窝，用自适应型局部调整算子+2-opt 优化代替莱维飞行成为鸟窝移动的策略，若新鸟窝适应度较大则保留，否则沿用旧鸟窝。当寄主发现鸟窝时，对该鸟窝实施全局随机扰动策略+2-opt 优化，若新鸟窝适应度较大则保留，否则沿用旧鸟窝。 3.1 表示方式 TSP 问题的向量表示方式分为三种：近邻表示、次序表示和路径表示。本文选取可与本文所采用的优化算子相结合的近邻表示，例如周游城市的顺序 C1 - C5 - C4 - C2 - C3 ，则算法的一个可行解记为 ( 3.2 路径初始化 1,5,4,2,3 。 ) 为加快算法的收敛速度，本文的路径初始化采用轮盘赌法，首先确定出发城市并建立禁忌表，按概率选择下一城市，与前一城市的距离越短则选择的概率越大，并将以已经访问过的城市加入禁忌表，下次不再访问，如此循环进行，直至禁忌表内包含所有城市。 3.3 评估函数在 TSP 问题中，路径长度越短则表示解的质量越高，即路径长度与解的适应度成反比，所以评价函数定义为路径长度的倒数，路径长度越大，评价函数的值越小，解的适应度就越低，路径长度越小，评价函数的值越大，解的适应度就越高。 3.4 自适应型局部调整算子针对离散型算法在求解 TSP 问题时对路径进行整体调整容易破坏已形成的较优路径，设计一种自适应型局部调整算子来对一条路径进行局部调整。设 C = {C1,C2,⋯,Cn} 为 n 个城市的 TSP 问题的一条路径，s 是一个输入参数，表示按每段 s 个城市个将路径 C 分为 ûn/s 段并还剩余 k = n%s 个城市称为剩余段，在 ë ûn/s 段 ë 中任意取两个城市，若 k ≥ 2 ，则也在剩余段中任意取两个城市。对于每一段所取出的城市，按 w,w ∈ ( 0,1 抉择是否进行交换，生成一个属于 ( 0,1 的随机数 r ，若 w > r 则交换取出的城市，否则不交换。通过大量实验证明参数 s 的选取会对算法的搜索精度有影响，事实上，在算法前期种群中的每个解与最优解是有一定距离的，需要以较大幅度的局部调整并结合 2-opt 优化使得种群中的每个解与最优解之间的距离缩小，所以 w 在算法前期取值较小，然而到了算法后期，优质的解都被保留了下来，种群中的解很可能只需微调就能达到最优解，所以 w 在算法后期取值较大。综上所述，w 的取值随算法迭代次数的变大而变大，是一个需要自适应的参 ) ) 数，w 的定义式如下： iter max _iter × ( amax - amin w = amin + （2）其中 amax 和 amin 是经验参数，经大量实验验证 amax = 0.9 ， amin = 0.5 时算法运行结果最佳，iter 表示当前迭代次数，max_iter 为最大迭代次数。 ) 自适应型局部调整算子伪代码如下： Begin for i = 1 to ë ûn/s 创建数组 cs[0..s - 1] for j =(i - 1) × s to i × s - 1 cs[ j] = C[ j] end for csp 和 csq 是 cs 中 2 个随机的城市 r 是一个 0 到 1 的随机数 If r > w Swap csp and csq end if end for if k ≥ 2 csp 和 csq 是 cs 中 2 个随机的城市 r 是一个 0 到 1 的随机数 If r > w Swap csp and csq end if end if end 3.5 全局随机扰动策略在布谷鸟搜索算法优化连续函数的过程中，当寄主发现新来鸟蛋时，采用随机偏好游走策略来保持种群的多样性。在 3.4 节提出的自适应型局部调整算子，只对路径的局部经行调整会导致在算法后期种群多样性的下降，使算法易于陷入早熟。在本文算法中，当寄主发现新来鸟蛋时以全局随机扰策略调整路径。全局随机扰策略为：按 3.4 节提出的方法将 C = {C1,C2,⋯,Cn} 进行分段，每段取两个城市，取一个随机偶整数 m ，若 k ≥ 2 ，则 m ∈ ( ûn/s ，然后从分好的城市段中随机取 m 段，将这 m 个城市段两两配对，分别与组内另一个城市段的选中城市进行对应交换。全局随机扰动策略伪代码如下： ûn/s + 1 ，否则 m ∈ ( 2,ë 2,ë ) ) Begin If k ≥ 2 创建规模为 ( else ûn/s + 1 × 2 的矩阵 re ë ) 创建规模为 ë ûn/s × 2 的矩阵 re end if for i = 1 to ë ûn/s 创建数组 cs[0..s - 1]

张子成，韩伟：求解 TSP 问题的自适应离散型布谷鸟算法 2017，53（10） 51 for j =(i - 1) × s to i × s - 1 cs[ j] = C[ j] end for csp 和 csq 是 cs 中 2 个随机的城市将 csp 和 csq 插入 re 的第 i 行 end for If k ≥ 2 创建一个随机数 m ∈ ( 创建数组 se[0..m - 1] 向 se 插入 m 个不同的从 2 到 ë 2,ë ûn/s + 1 ) ûn/s + 1 的正整数 else 创建一个随机数 m ∈ ( 创建数组 se[0..m - 1] 向 se 插入 m 个不同的从 2 到 ë ûn/s 2,ë ) ûn/s 的正整数 end if num = 0 while num < m swap C[re[se[num]][0]] and C[re[se[num + 1]][0]] swap C[re[se[num]][1]] and C[re[se[num + 1]][1]] num = num + 2 ； end while end 3.6 算法描述步骤 1（设置算法参数）发现概率 Pa ，最大迭代次数 max_iter ，经验参数 amax 和 amin ，鸟窝数 N ，每段的城市数 s 。用 3.2 节方法生成初始路径，并以 3.1 节所提表示方法对解进行编码，并计算出每个解的适应度。步骤 2 对每个鸟窝内的解用 3.4 节的自适应型局部调整算子经行局部调整后再用 2-opt 优化调整后的路径，计算机新路径的适应度，若比原路径适应度大则用新路径替换原路径，若比原路径适应度小则丢弃，若当前路径适应度比全局最优解大，以当前路径为全局最优解。步骤 3 计算每个鸟窝的发现概率，若鸟窝被发现，则用 3.5 节的全局随机扰动策略对该鸟窝内的路径进行全局的扰动并用 2-opt 优化扰动后的路径，若比原路径适应度大则用扰动后路径替换原路径，若比原路径适应度小则丢弃。若当前路径适应度比全局最优解大，以当前路径为全局最优解。步骤 4 检查算法是否到达最大迭代次数，若到达，停止算法，输出全局最优解，若未到达重复步骤 2、步骤 3。 4 算法的性能测试及仿真实验 4.1 算法参数设置平衡算法全局寻优能与局部寻优能力的关键在于输入参数 S 。若 S 较大，城市序列分段较稀疏，扰动效果不明显；若 S 较小，城市序列分段较密集，降低了算法的局部收敛性。经大量实验表明对于不同规模的算例 S 取 10 时算法运行效果均最优。表 1 参数取值列表 Pa 0.2 amax 0.9 amin 0.4 N 20 max _iter 500 s 10 4.2 对比分析表中所用数据名称说明，已知最优为该 TSP 算例目前已知的最优解，最优解表示用算法所解出的 TSP 最优值，平均值为每次运行的最优值之和除以次数，“—”表示算例的已知最优不存在或者算法所解出的最优解优于已知最优解。最优解偏差率计算公式如下：最优解偏差率 = 最优解 - 已知最优已知最优 × 100% 表 2 为本文 ADCS 与 DCS[14]的求解质量对比表，表中 11个算例是从文献[14]中挑选的不同规模的 TSP问题， ADCS 算法连续运行 30 次。由于文献[14]采用的是整型最优解，其值会略微大于浮点型最优解，而从表 2 中可以发现 ADCS 对于 11 个不同规模的 TSP 算例的最优解在算例 Pr76 KroB100 Pr107 Pr136 KroB200 Lin318 Pr439 Rat575 Rat783 Pr1002 Nrw1379 已知最优 108 159.0 22 141.0 44 303.0 96 772.0 29 437.0 42 029.0 107 217.0 6 773.0 8 806.0 259 045.0 56 638.0 表 2 ADCS 与 DCS 求解质量对比表最优解平均值 DCS 108 159.0 22 141.0 44 303.0 96 790.0 29 448.0 42 125.0 107 447.0 6 896.0 9 043.0 266 508.0 5 8951.0 ADCS 108 159.4 22 139.1 44 301.7 96 780.5 29 441.0 42 042.5 107 251.6 6 891.0 9 015.9 263 757.3 58 404.4 DCS 108 159.0 22 141.5 44 307.0 97 009.2 29 542.5 42 434.7 107 960.5 6 956.7 9 109.3 268 630.0 59 349.5 ADCS 108 159.4 22 139.1 44 301.7 96 869.8 29 456.4 42 167.8 107 801.4 6 923.3 9 043.0 264 793.8 58 604.7 最优解偏差率/% DCS ADCS — — — — — — 0.019 0.037 0.228 0.215 1.816 2.691 2.881 4.084 0.009 0.014 0.031 0.032 1.742 2.373 1.819 3.118

52 2017，53（10） Computer Engineering and Applications 计算机工程与应用数值上均小于 DCS，即 ADCS 对于求解不同规模的 TSP 问题的求解精度更高。随着 TSP 问题的规模不断增加， ADCS 求解精度的优势愈发明显。对于算例 Pr1002， ADCS 所求最优解比 DCS 所求最优解少 2 750.7；对于算例 Nrw1379，ADCS 所求最优解比 DCS 所求最优解少 546.6。在表 2 中，ADCS 所求的平均值与最优解更为贴近，所以相比于 DCS，ADCS 具有更强的稳定性。表 3 为本文 ADCS 与 HGA[12]的求解质量对比，由于对于小规模 TSP 问题 ADCS 与 HGA 均可以很快地收敛到已知最优解，故选取 11 个中小型规模的 TSP 问题进行对比。从表 3 中可以看出，对于规模小于 200 的 TSP 问题，ADCS 与 HGA 均有着很好的表现，能收敛到已知最优解（由于本文与文献[12]均采取浮点型最优解，所以结果会略大于已知最优解），但是随着 TSP 问题规模的增加，ADCS 在求解精度方面的优势较为明显。对于算例 Ts255，HGA 的偏差率达 1.184% ，而 ADCS 则为 0.002%，几乎可以忽略不计；对于算例 Pr299，HGA 的偏差率达 2.637%，而 ADCS则为 0.077%，仅为 HGA的 1/34；对于算例 Rd400，HGA 的偏差率达 5.029%，而 ADCS 则为 0.321%，仅为 HGA 的 1/16。此外，ADCS 所求的平均值与最优解更为接近，所以相比于 HGA，ADCS 具有更强的稳定性。表 4 为本文 ADCS 与 OMACO [10]的求解质量对比，从文献[10]中选取规模不同的 19 个算例与本文算法进行对比发现对于不同规模的 TSP 问题，ADCS 较 OMACO 在求解精度上均有较大的提升。特别地，对于算例 Eil101、Ch150、Tsp225 和 Ali535，本文算法发现了比已知最优解更为优质的解。算例已知最优 Berlin52 Rat99 Ch130 D198 Ts225 Pr226 A280 Pr299 Linhp318 Rd400 Pcb442 7 542.0 1 211.0 6 110.0 15 780.0 126 643.0 80 369.0 2 579.0 48 191.0 41 345.0 15 281.0 50 778.0 表 3 ADCS 与 HGA 求解质量对比表最优解平均值 HGA 7 544.4 1 219.2 6 110.7 15 897.0 128 141.9 80 436.0 2 659.8 49 462.4 43 050.7 16 049.6 52 874.3 ADCS 7 544.4 1 219.2 6 110.7 15 809.4 126 645.9 80 370.3 2 586.8 48 228.0 42 082.4 15 330.1 51 075.9 HGA 7 544.4 1 228.9 6 130.3 15 963.3 128 295.7 80 534.4 2 676.1 49 757.7 43 247.1 16 144.0 53 016.2 ADCS 7 544.4 1 219.2 6 116.3 15 816.3 126 649.4 80 370.3 2 590.0 48 321.0 42 236.2 15 423.2 51 283.2 表 4 ADCS 与 OMACO 求解质量对比表最优解偏差率/% HGA ADCS 0.032 0.032 0.677 0.677 0.011 0.011 0.741 0.186 0.002 1.184 0.002 0.083 0.302 3.133 2.637 0.077 1.784 4.124 0.321 5.029 4.128 0.585 算例 St70 KroA100 KroD100 KroE100 Eil101 Bier127 Ch150 KroA200 Gr202 Tsp225 Fl417 D493 Ali535 U574 P654 D657 Gr666 U724 Vm1084 已知最优 675.0 21 282.0 21 294.0 22 068.0 642.3 118 282.0 6 532.3 29 368.0 — 3 916.0 11 861.0 35 002.0 2 023.4 36 905.0 34 643.0 48 912.0 2 943.6 41 910.0 239 297.0 最优解最优解偏差率/% OMACO 678.6 21 321.0 21 415.9 22 107.5 642.0 118 767.5 6 546.9 29 457.7 489.0 3 894.5 11 991.2 36 146.5 2 093.3 38 603.4 37 118.8 53 096.0 3 240.3 44 408.3 250 172.2 ADCS 677.1 21 285.4 21 294.3 22 068.8 640.2 118 293.5 6 530.9 29 369.4 486.5 3 867.6 11 927.5 35 243.5 2 016.0 37 311.7 34 697.4 49 371.5 3 113.1 42 416.5 241 318.5 OMACO 0.533 0.183 0.572 0.179 — 0.411 0.224 0.305 — — 1.098 3.269 3.455 4.602 7.147 8.554 10.08 5.961 4.545 ADCS 0.311 0.016 0.001 0.004 — 0.009 — 0.005 — — 0.561 0.690 — 1.102 0.157 0.939 5.758 1.209 0.845

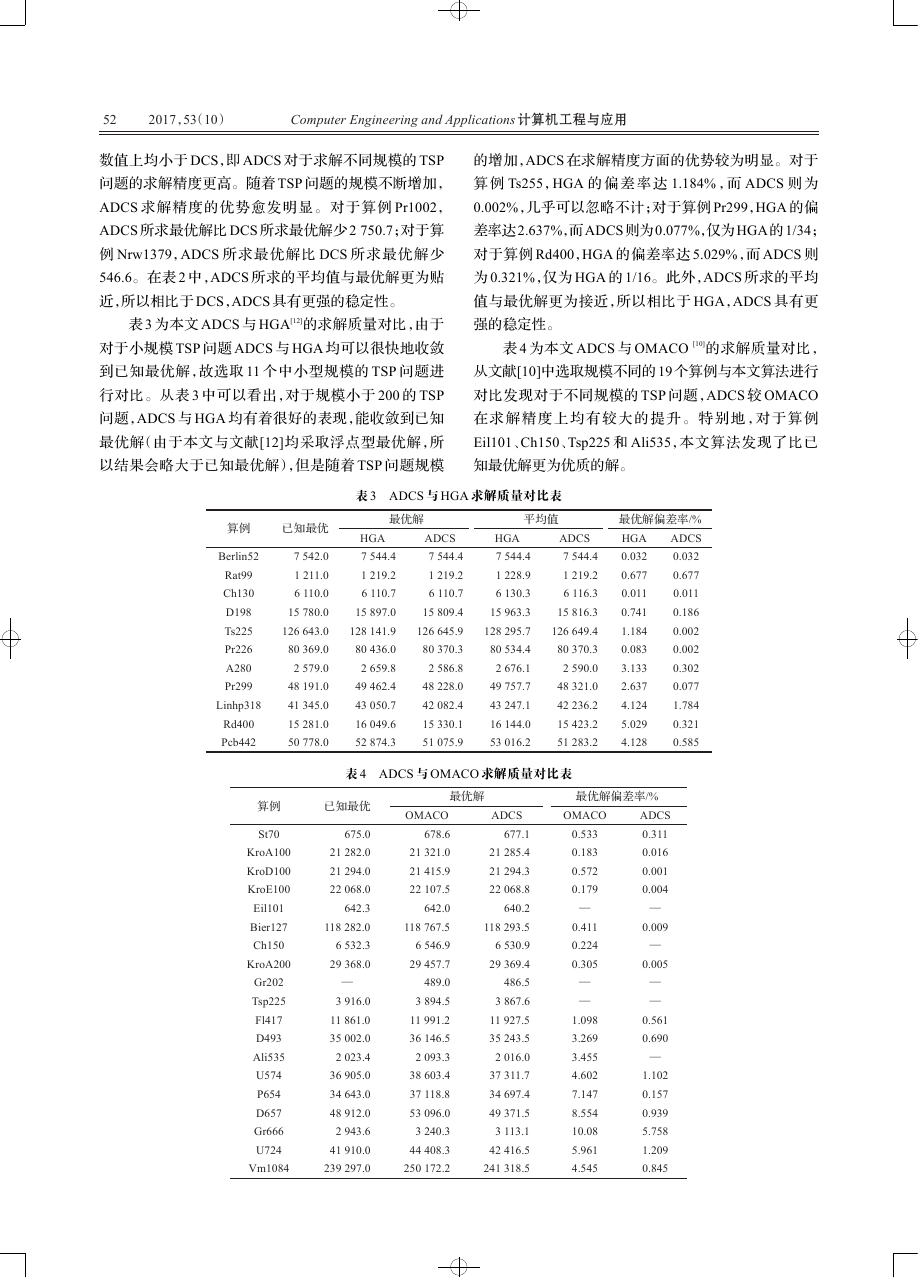
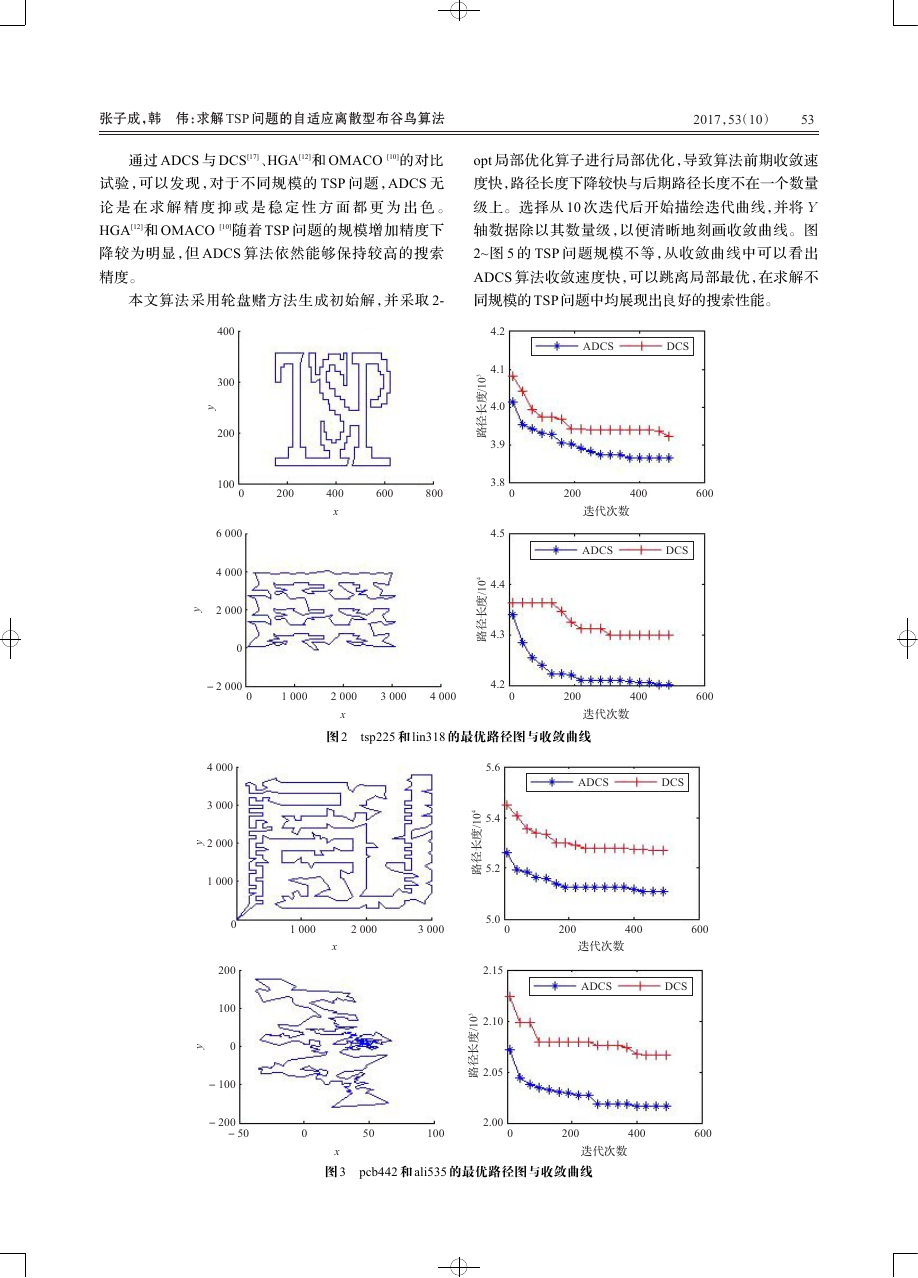
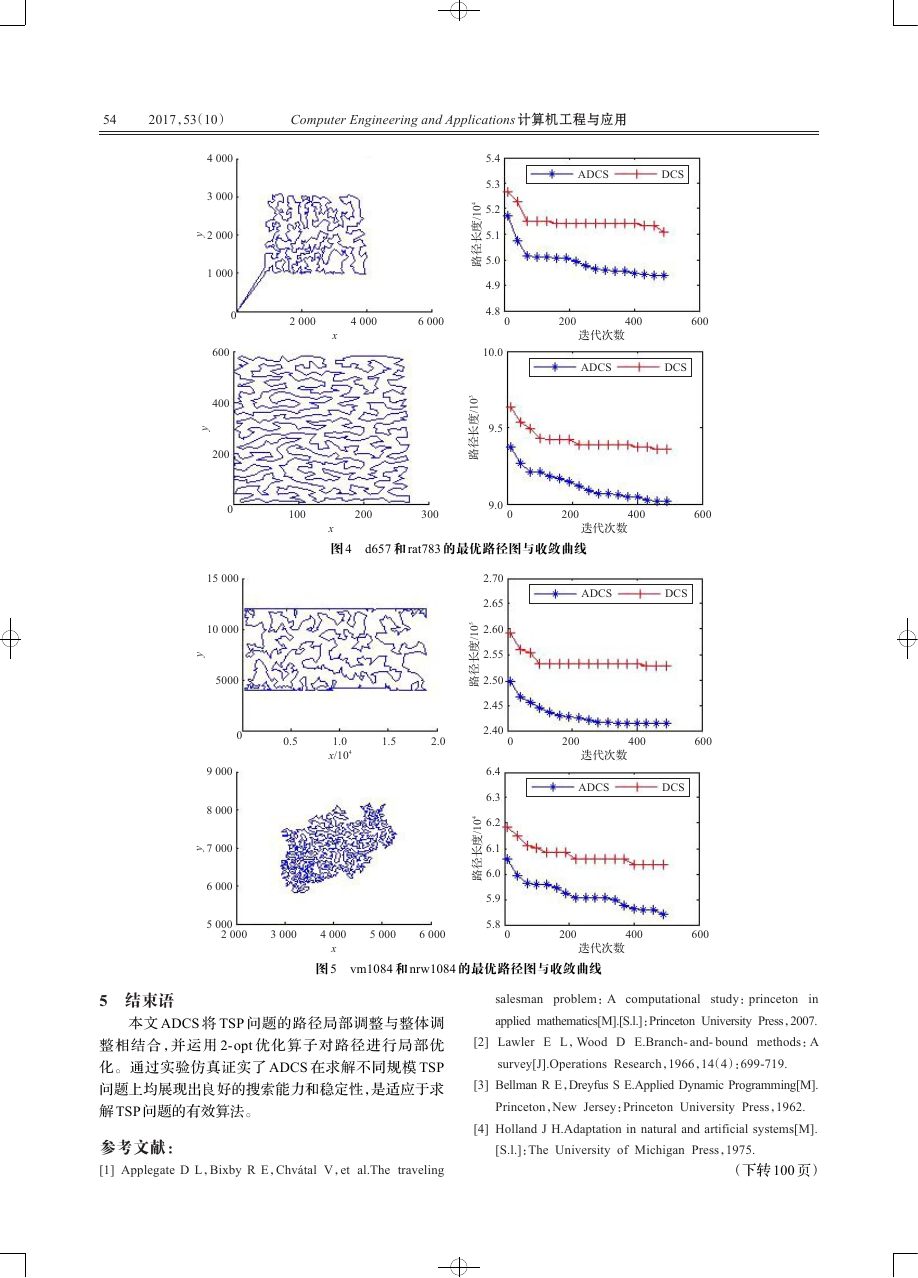
张子成，韩伟：求解 TSP 问题的自适应离散型布谷鸟算法 2017，53（10） 53 通过 ADCS 与 DCS[17]、HGA[12]和 OMACO [10]的对比试验，可以发现，对于不同规模的 TSP 问题，ADCS 无论是在求解精度抑或是稳定性方面都更为出色。 HGA[12]和 OMACO [10]随着 TSP 问题的规模增加精度下降较为明显，但 ADCS 算法依然能够保持较高的搜索精度。本文算法采用轮盘赌方法生成初始解，并采取 2- opt 局部优化算子进行局部优化，导致算法前期收敛速度快，路径长度下降较快与后期路径长度不在一个数量级上。选择从 10 次迭代后开始描绘迭代曲线，并将 Y 轴数据除以其数量级，以便清晰地刻画收敛曲线。图 2~图 5 的 TSP 问题规模不等，从收敛曲线中可以看出 ADCS 算法收敛速度快，可以跳离局部最优，在求解不同规模的 TSP 问题中均展现出良好的搜索性能。 400 300 200 y ADCS DCS 4.2 4.1 4.0 3.9 3 0 1 / 度长径路 100 0 200 400 x 600 800 3.8 0 200 400 600 迭代次数 6 000 4 000 y 2 000 0 －2 000 0 1 000 2 000 3 000 4 000 x 4.5 4.4 4.3 4 0 1 / 度长径路 4.2 0 ADCS DCS 200 400 600 迭代次数图 2 tsp225 和 lin318 的最优路径图与收敛曲线 4 000 3 000 2 000 y 1 000 0 200 100 y 0 －100 －200 －50 1 000 2 000 3 000 x 0 50 100 5.6 5.4 5.2 4 0 1 / 度长径路 5.0 0 2.15 2.10 2.05 2.00 0 3 0 1 / 度长径路 ADCS DCS 200 400 600 迭代次数 ADCS DCS 200 400 600 迭代次数 x 图 3 pcb442 和 ali535 的最优路径图与收敛曲线

54 2017，53（10） Computer Engineering and Applications 计算机工程与应用 2 000 4 000 6 000 x ADCS DCS 0 200 400 迭代次数 600 ADCS DCS 5.4 5.3 5.2 5.1 5.0 4.9 4.8 10.0 9.5 4 0 1 / 度长径路 3 0 1 / 度长径路 100 200 300 9.0 0 x 图 4 d657 和 rat783 的最优路径图与收敛曲线 200 400 迭代次数 600 4 000 3 000 2 000 y 1 000 0 600 400 200 0 y 15 000 10 000 y 5000 2.70 2.65 2.60 2.55 2.50 2.45 2.40 6.4 6.3 6.2 6.1 6.0 5.9 5.8 5 0 1 / 度长径路 4 0 1 / 度长径路 ADCS DCS 0 200 400 迭代次数 600 ADCS DCS 0 200 400 迭代次数 600 0 0.5 1.0 x/104 1.5 2.0 9 000 8 000 7 000 y 6 000 5 000 2 000 3 000 4 000 5 000 6 000 x 图 5 vm1084 和 nrw1084 的最优路径图与收敛曲线 5 结束语本文 ADCS 将 TSP 问题的路径局部调整与整体调整相结合，并运用 2-opt 优化算子对路径进行局部优化。通过实验仿真证实了 ADCS 在求解不同规模 TSP 问题上均展现出良好的搜索能力和稳定性，是适应于求解 TSP 问题的有效算法。参考文献： [1] Applegate D L，Bixby R E，Chvátal V，et al.The traveling salesman problem：A computational study：princeton in applied mathematics[M].[S.l.]：Princeton University Press，2007. [2] Lawler E L，Wood D E.Branch- and- bound methods：A survey[J].Operations Research，1966，14（4）：699-719. [3] Bellman R E，Dreyfus S E.Applied Dynamic Programming[M]. Princeton，New Jersey：Princeton University Press，1962. [4] Holland J H.Adaptation in natural and artificial systems[M]. [S.l.]：The University of Michigan Press，1975. （下转 100 页）

分享到：

赞收藏

资料库

论文研究-求解TSP问题的自适应离散型布谷鸟算法.pdf

相关推荐

开发技术

热门标签

最新资料