logo资料库

斯坦福UFLDL深度学习课程翻译版合集.pdf

发布时间：2022-06-12 发布人：admin 分类：说明书 资料大小：5.18M 资料格式：pdf 举报 版权申诉
第1页 / 共166页
第2页 / 共166页
第3页 / 共166页
第4页 / 共166页
第5页 / 共166页
第6页 / 共166页
第7页 / 共166页
第8页 / 共166页
资料共166页，剩余部分请下载后查看
    1/166UFLDL教程http://deeplearning.stanford.edu/wiki/index.php/UFLDL%E6%95%99%E7%A8%8B说明：本教程将阐述无监督特征学习和深度学习的主要观点。通过学习，你也将实现多个功能学习/深度学习算法，能看到它们为你工作，并学习如何应用/适应这些想法到新问题上。本教程假定机器学习的基本知识（特别是熟悉的监督学习，逻辑回归，梯度下降的想法），如果你不熟悉这些想法，我们建议你去这里机器学习课程，并先完成第II，III，IV章（到逻辑回归）。1稀疏自编码器1.1神经网络1.2反向传导算法1.3梯度检验与高级优化1.4自编码算法与稀疏性1.5可视化自编码器训练结果1.6稀疏自编码器符号一览表1.7Exercise:SparseAutoencoder2矢量化编程实现2.1矢量化编程2.2逻辑回归的向量化实现样例2.3神经网络向量化2.4Exercise:Vectorization3预处理：主成分分析与白化3.1主成分分析3.2白化3.3实现主成分分析和白化3.4Exercise:PCAin2D3.5Exercise:PCAandWhitening4Softmax回归4.1Softmax回归4.2Exercise:SoftmaxRegression5自我学习与无监督特征学习5.1自我学习5.2Exercise:Self-TaughtLearning
    2/1666建立分类用深度网络6.1从自我学习到深层网络6.2深度网络概览6.3栈式自编码算法6.4微调多层自编码算法6.5Exercise:Implementdeepnetworksfordigitclassification7自编码线性解码器7.1线性解码器7.2Exercise:LearningcolorfeatureswithSparseAutoencoders8处理大型图像8.1卷积特征提取8.2池化8.3Exercise:ConvolutionandPooling注意:这条线以上的章节是稳定的。下面的章节仍在建设中，如有变更，恕不另行通知。请随意浏览周围并欢迎提交反馈/建议。9混杂的9.1MATLABModules9.2StyleGuide9.3UsefulLinks10混杂的主题10.1数据预处理10.2用反向传导思想求导进阶主题:11稀疏编码11.1稀疏编码11.2稀疏编码自编码表达11.3Exercise:SparseCoding12独立成分分析样式建模12.1独立成分分析12.2Exercise:IndependentComponentAnalysis13其它13.1Convolutionaltraining13.2RestrictedBoltzmannMachines
    3/16613.3DeepBeliefNetworks13.4DenoisingAutoencoders13.5K-means13.6Spatialpyramids/Multiscale13.7SlowFeatureAnalysis13.8TiledConvolutionNetworks英文原文作者:AndrewNg,JiquanNgiam,ChuanYuFoo,YifanMai,CarolineSuen神经网络Contents1概述2神经网络模型3中英文对照4中文译者概述以监督学习为例，假设我们有训练样本集，那么神经网络算法能够提供一种复杂且非线性的假设模型，它具有参数，可以以此参数来拟合我们的数据。为了描述神经网络，我们先从最简单的神经网络讲起，这个神经网络仅由一个“神经元”构成，以下即是这个“神经元”的图示：
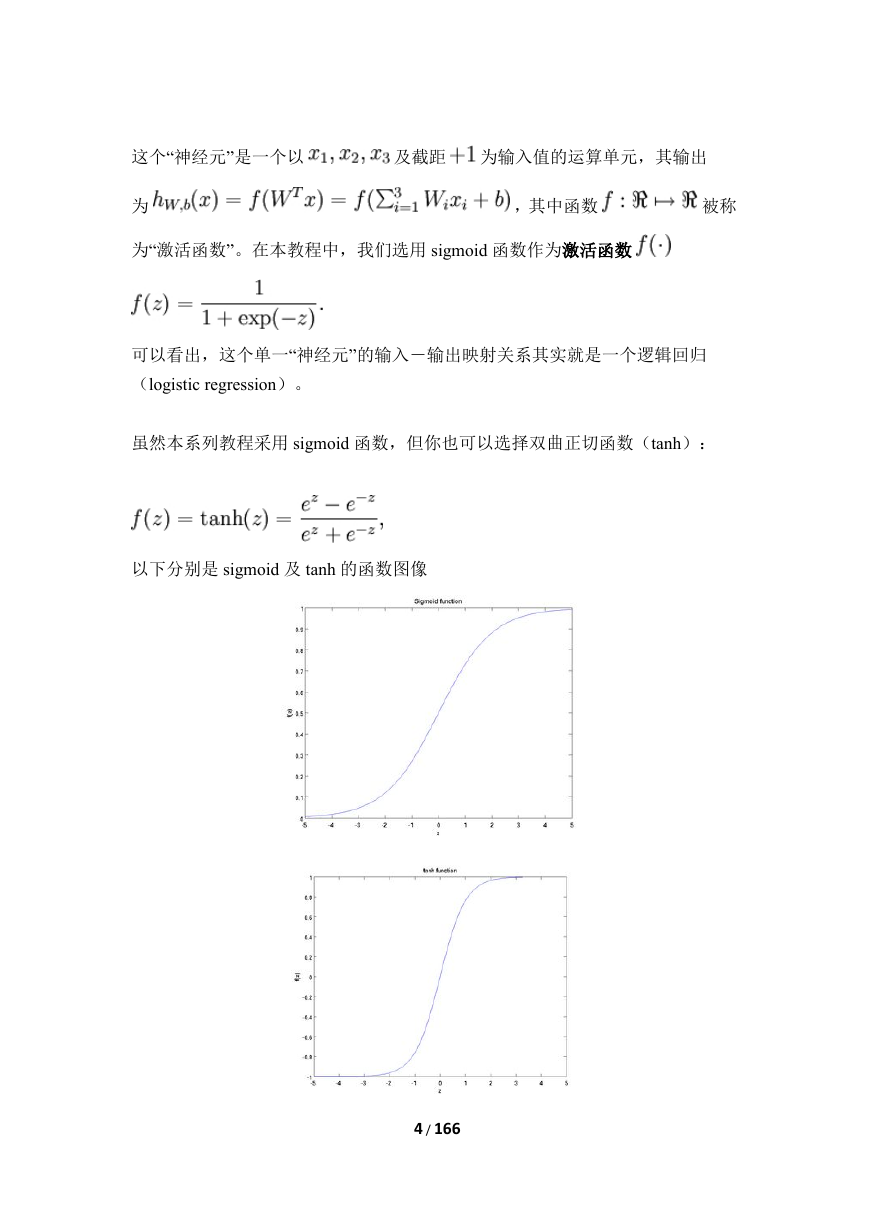
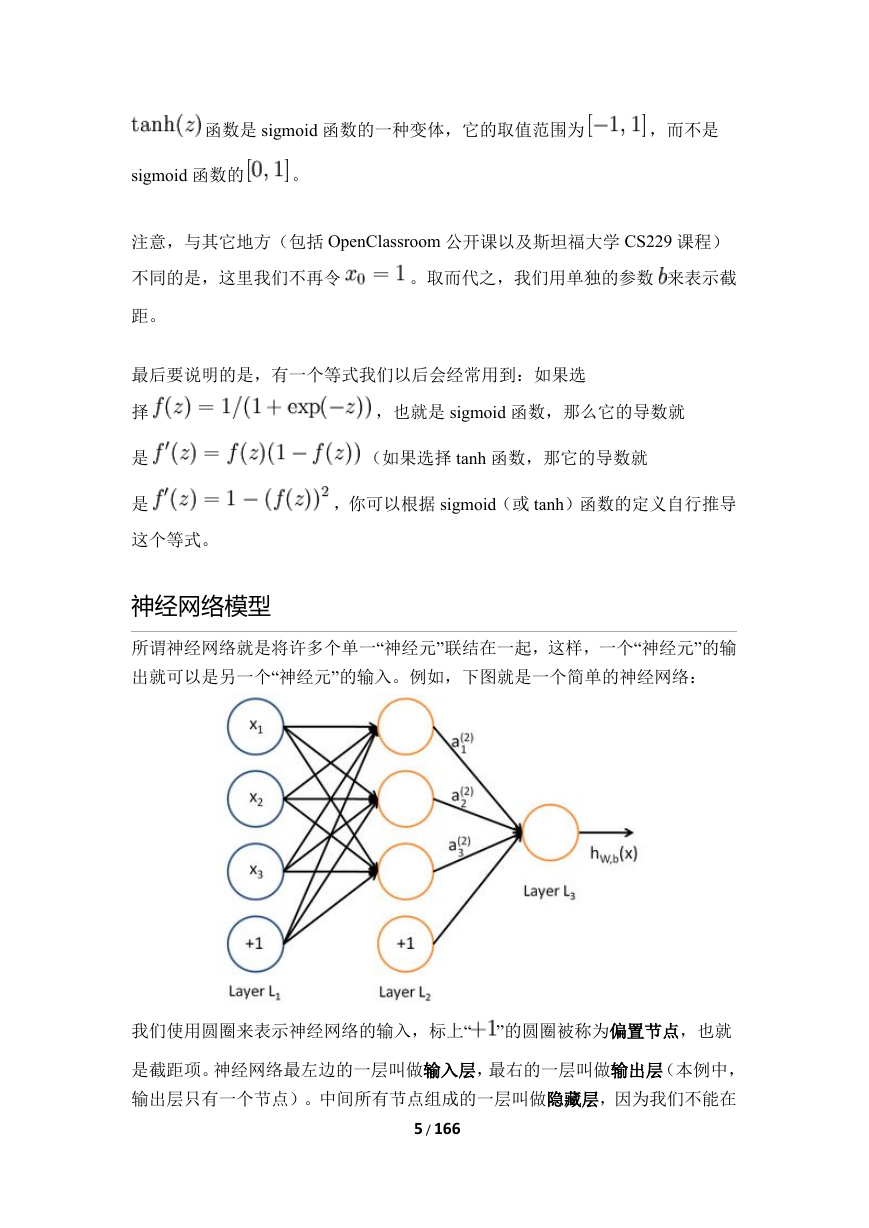
    4/166这个“神经元”是一个以及截距为输入值的运算单元，其输出为，其中函数被称为“激活函数”。在本教程中，我们选用sigmoid函数作为激活函数可以看出，这个单一“神经元”的输入－输出映射关系其实就是一个逻辑回归（logisticregression）。虽然本系列教程采用sigmoid函数，但你也可以选择双曲正切函数（tanh）：以下分别是sigmoid及tanh的函数图像
    5/166函数是sigmoid函数的一种变体，它的取值范围为，而不是sigmoid函数的。注意，与其它地方（包括OpenClassroom公开课以及斯坦福大学CS229课程）不同的是，这里我们不再令。取而代之，我们用单独的参数来表示截距。最后要说明的是，有一个等式我们以后会经常用到：如果选择，也就是sigmoid函数，那么它的导数就是（如果选择tanh函数，那它的导数就是，你可以根据sigmoid（或tanh）函数的定义自行推导这个等式。神经网络模型所谓神经网络就是将许多个单一“神经元”联结在一起，这样，一个“神经元”的输出就可以是另一个“神经元”的输入。例如，下图就是一个简单的神经网络：我们使用圆圈来表示神经网络的输入，标上“”的圆圈被称为偏置节点，也就是截距项。神经网络最左边的一层叫做输入层，最右的一层叫做输出层（本例中，输出层只有一个节点）。中间所有节点组成的一层叫做隐藏层，因为我们不能在
    6/166训练样本集中观测到它们的值。同时可以看到，以上神经网络的例子中有3个输入单元（偏置单元不计在内），3个隐藏单元及一个输出单元。我们用来表示网络的层数，本例中，我们将第层记为，于是是输入层，输出层是。本例神经网络有参数，其中（下面的式子中用到）是第层第单元与第层第单元之间的联接参数（其实就是连接线上的权重，注意标号顺序），是第层第单元的偏置项。因此在本例中，，。注意，没有其他单元连向偏置单元(即偏置单元没有输入)，因为它们总是输出。同时，我们用表示第层的节点数（偏置单元不计在内）。我们用表示第层第单元的激活值（输出值）。当时，，也就是第个输入值（输入值的第个特征）。对于给定参数集合，我们的神经网络就可以按照函数来计算输出结果。本例神经网络的计算步骤如下：我们用表示第层第单元输入加权和（包括偏置单元），比如，，则。这样我们就可以得到一种更简洁的表示法。这里我们将激活函数扩展为用
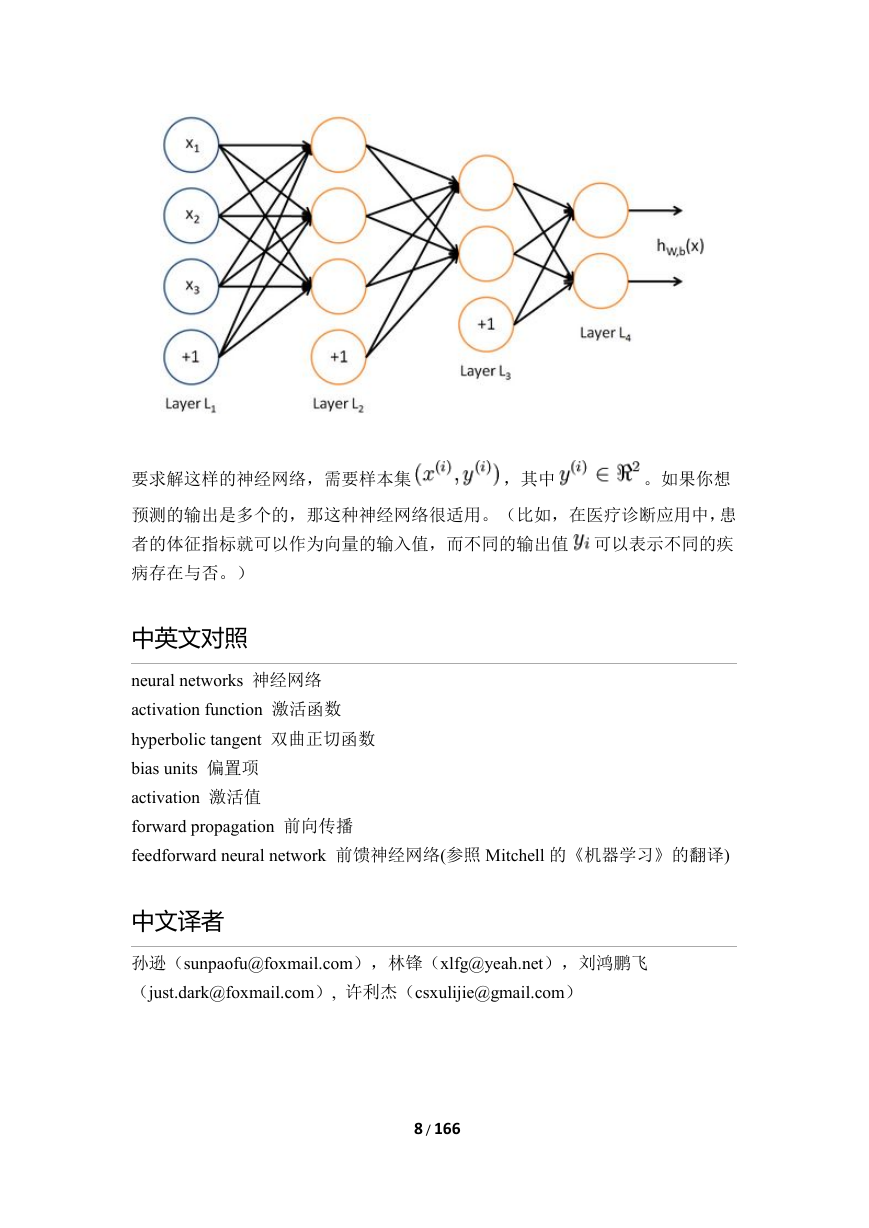
    7/166向量（分量的形式）来表示，即，那么，上面的等式可以更简洁地表示为：我们将上面的计算步骤叫作前向传播。回想一下，之前我们用表示输入层的激活值，那么给定第层的激活值后，第层的激活值就可以按照下面步骤计算得到：将参数矩阵化，使用矩阵－向量运算方式，我们就可以利用线性代数的优势对神经网络进行快速求解。目前为止，我们讨论了一种神经网络，我们也可以构建另一种结构的神经网络（这里结构指的是神经元之间的联接模式），也就是包含多个隐藏层的神经网络。最常见的一个例子是层的神经网络，第层是输入层，第层是输出层，中间的每个层与层紧密相联。这种模式下，要计算神经网络的输出结果，我们可以按照之前描述的等式，按部就班，进行前向传播，逐一计算第层的所有激活值，然后是第层的激活值，以此类推，直到第层。这是一个前馈神经网络的例子，因为这种联接图没有闭环或回路。神经网络也可以有多个输出单元。比如，下面的神经网络有两层隐藏层：及，输出层有两个输出单元。
    8/166要求解这样的神经网络，需要样本集，其中。如果你想预测的输出是多个的，那这种神经网络很适用。（比如，在医疗诊断应用中，患者的体征指标就可以作为向量的输入值，而不同的输出值可以表示不同的疾病存在与否。）中英文对照neuralnetworks神经网络activationfunction激活函数hyperbolictangent双曲正切函数biasunits偏置项activation激活值forwardpropagation前向传播feedforwardneuralnetwork前馈神经网络(参照Mitchell的《机器学习》的翻译)中文译者孙逊（sunpaofu@foxmail.com），林锋（xlfg@yeah.net），刘鸿鹏飞（just.dark@foxmail.com）,许利杰（csxulijie@gmail.com）
    分享到：
    赞 收藏

    相关推荐

    资料库

    课程资源

    共收录17145份资料，累计13个分类，关注成员有19位，主要包括：PHP,网络管理,网页制作,Java,.Net,数据库,3G/移动开发,C/C++,游戏开发,嵌入式,讲义,软件测试,专业指导

    热门标签

    PHP 网络管理 网页制作 Java .Net 数据库 3G/移动开发 C/C++ 游戏开发 嵌入式 讲义 软件测试 专业指导

    最新资料