第1页 / 共24页
第2页 / 共24页
第3页 / 共24页
第4页 / 共24页
第5页 / 共24页
第6页 / 共24页
第7页 / 共24页
第8页 / 共24页
中国矿业大学常俊林版《自动控制原理》1-6章课后习题解答.doc
第一章
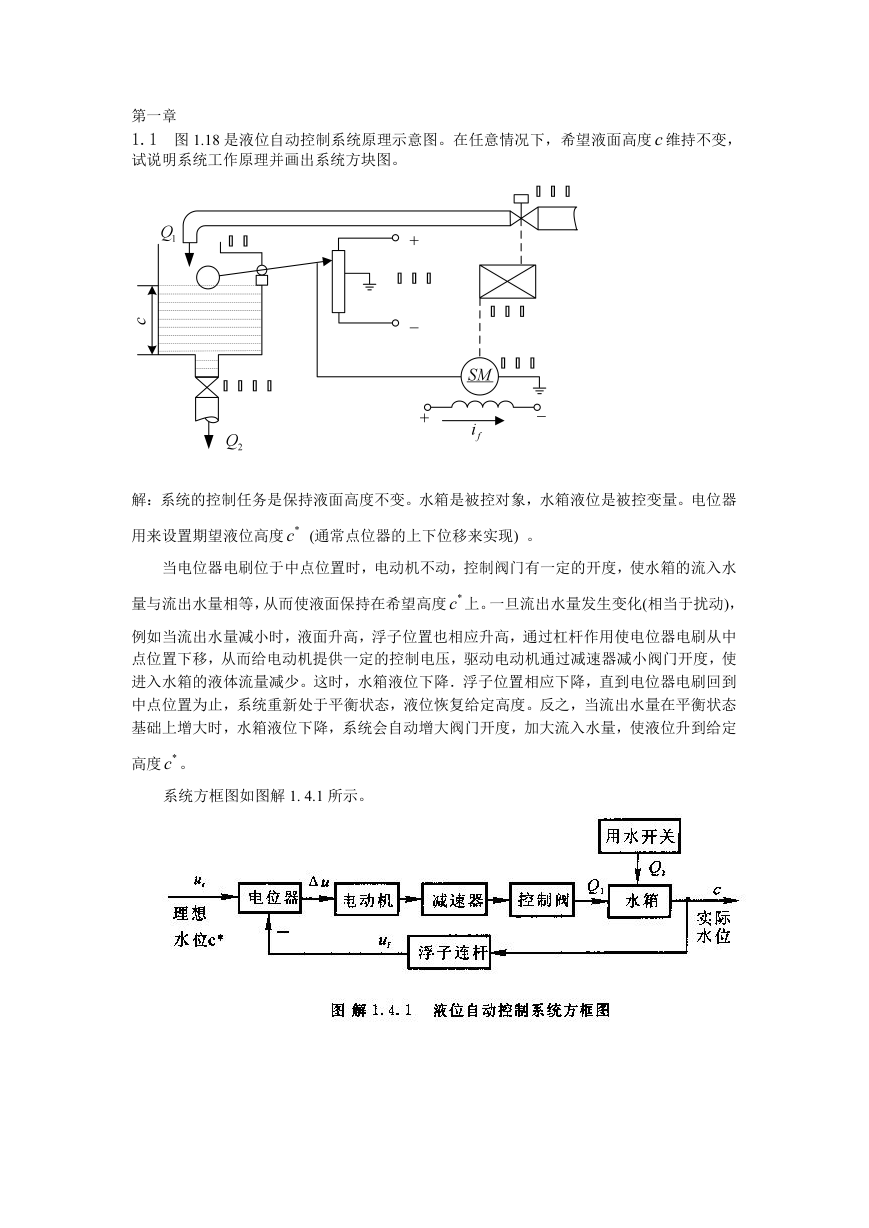
1.1 图 1.18 是液位自动控制系统原理示意图。在任意情况下，希望液面高度 c 维持不变，
试说明系统工作原理并画出系统方块图。
解：系统的控制任务是保持液面高度不变。水箱是被控对象，水箱液位是被控变量。电位器
用来设置期望液位高度 *c (通常点位器的上下位移来实现) 。
当电位器电刷位于中点位置时，电动机不动，控制阀门有一定的开度，使水箱的流入水
量与流出水量相等，从而使液面保持在希望高度 *c 上。一旦流出水量发生变化(相当于扰动)，
例如当流出水量减小时，液面升高，浮子位置也相应升高，通过杠杆作用使电位器电刷从中
点位置下移，从而给电动机提供一定的控制电压，驱动电动机通过减速器减小阀门开度，使
进入水箱的液体流量减少。这时，水箱液位下降．浮子位置相应下降，直到电位器电刷回到
中点位置为止，系统重新处于平衡状态，液位恢复给定高度。反之，当流出水量在平衡状态
基础上增大时，水箱液位下降，系统会自动增大阀门开度，加大流入水量，使液位升到给定
高度 *c 。
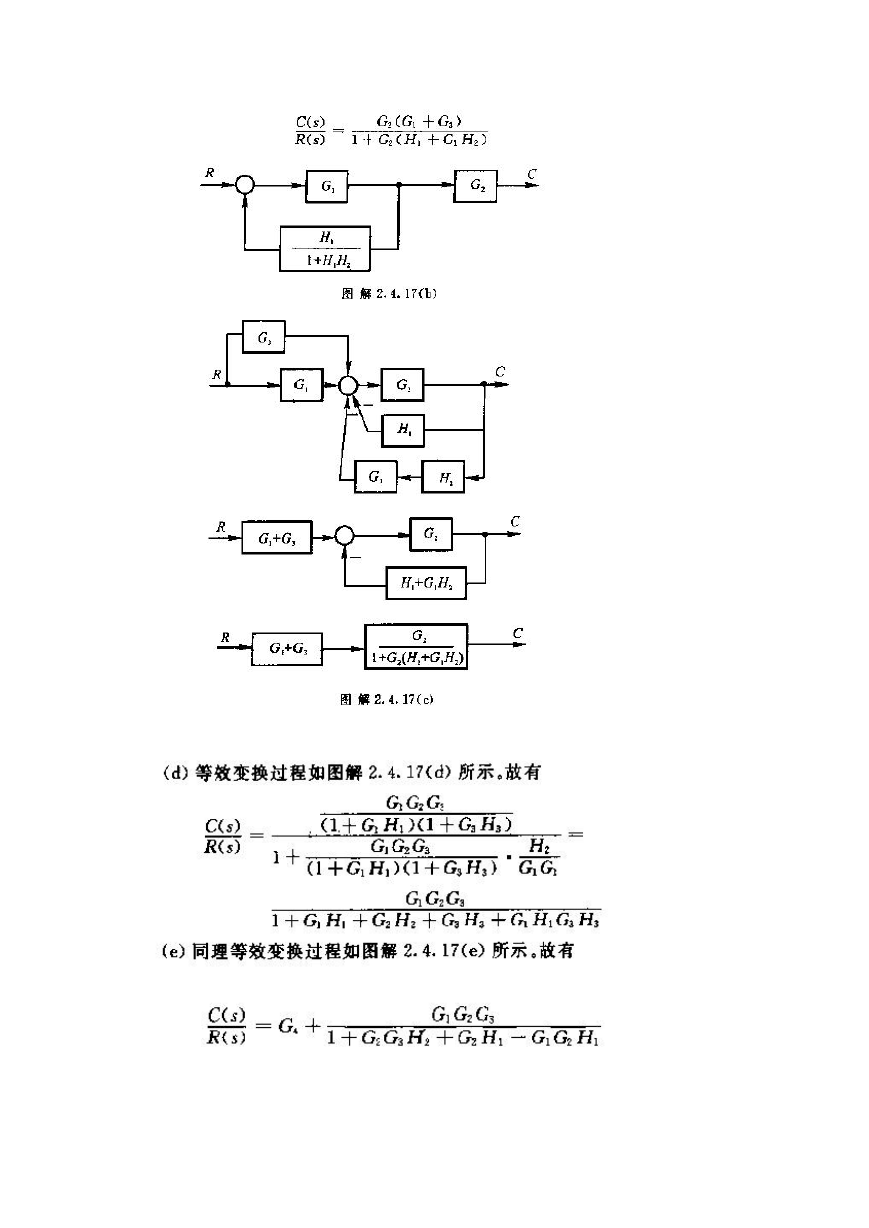
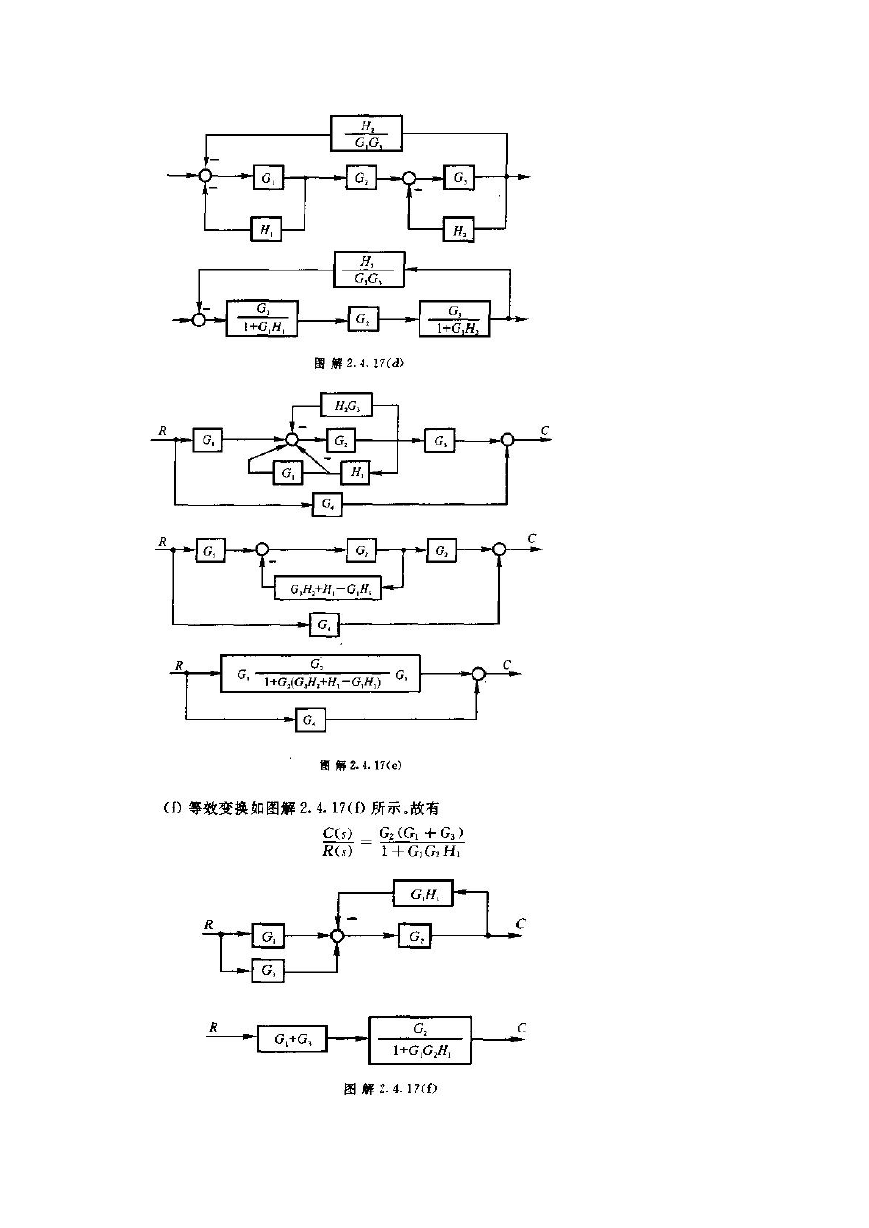
系统方框图如图解 1. 4.1 所示。
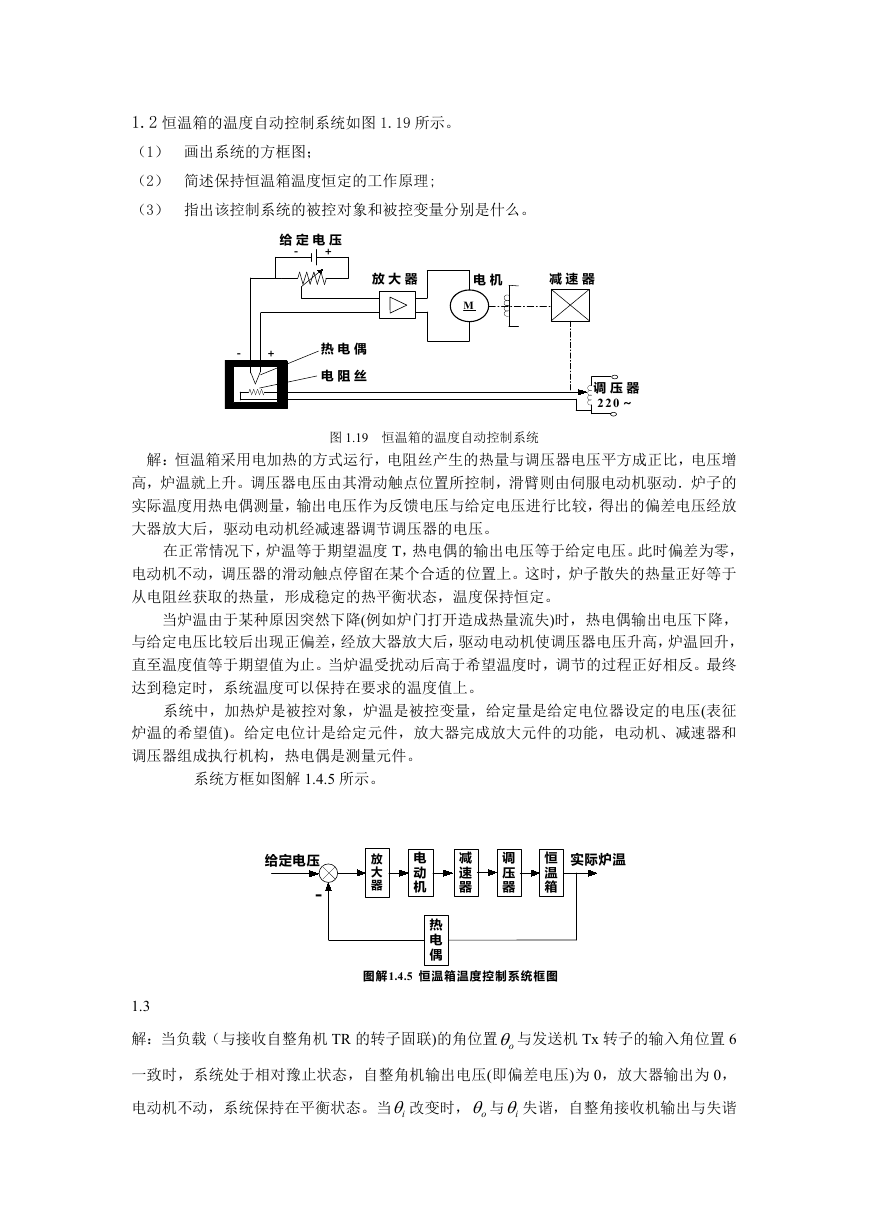
1.2 恒温箱的温度自动控制系统如图 1.19 所示。
（1） 画出系统的方框图；
（2） 简述保持恒温箱温度恒定的工作原理;
（3） 指出该控制系统的被控对象和被控变量分别是什么。
给 定 电 压
－ ＋
－ ＋
热 电 偶
电 阻 丝
放 大 器
电 机
减 速 器
M
调 压 器
220～
图 1.19 恒温箱的温度自动控制系统
解：恒温箱采用电加热的方式运行，电阻丝产生的热量与调压器电压平方成正比，电压增
高，炉温就上升。调压器电压由其滑动触点位置所控制，滑臂则由伺服电动机驱动．炉子的
实际温度用热电偶测量，输出电压作为反馈电压与给定电压进行比较，得出的偏差电压经放
大器放大后，驱动电动机经减速器调节调压器的电压。
在正常情况下，炉温等于期望温度 T，热电偶的输出电压等于给定电压。此时偏差为零，
电动机不动，调压器的滑动触点停留在某个合适的位置上。这时，炉子散失的热量正好等于
从电阻丝获取的热量，形成稳定的热平衡状态，温度保持恒定。
当炉温由于某种原因突然下降(例如炉门打开造成热量流失)时，热电偶输出电压下降，
与给定电压比较后出现正偏差，经放大器放大后，驱动电动机使调压器电压升高，炉温回升，
直至温度值等于期望值为止。当炉温受扰动后高于希望温度时，调节的过程正好相反。最终
达到稳定时，系统温度可以保持在要求的温度值上。
系统中，加热炉是被控对象，炉温是被控变量，给定量是给定电位器设定的电压(表征
炉温的希望值)。给定电位计是给定元件，放大器完成放大元件的功能，电动机、减速器和
调压器组成执行机构，热电偶是测量元件。
系统方框如图解 1.4.5 所示。
给定电压
-
放
大
器
电
动
机
减
速
器
调
压
器
恒
温
箱
实际炉温
热
电
偶
图解1.4.5 恒温箱温度控制系统框图
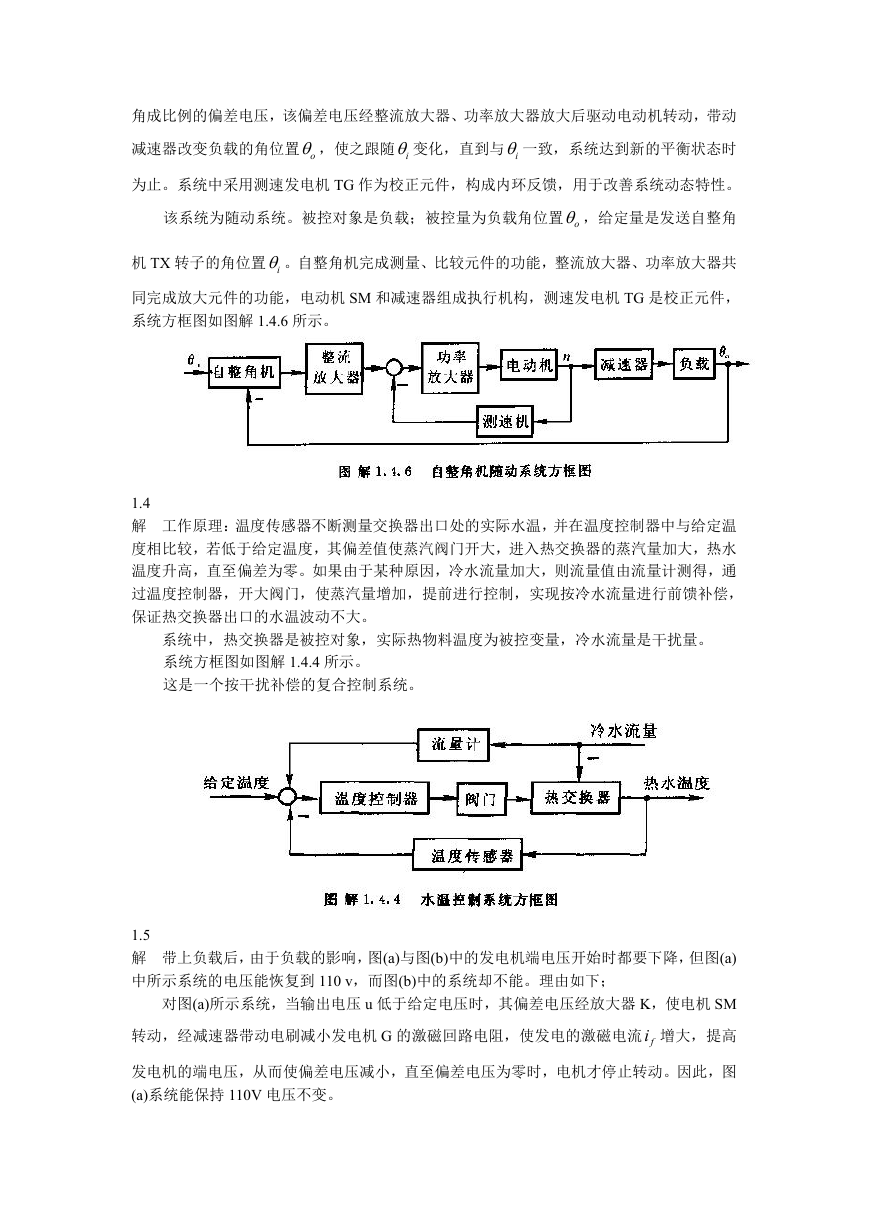
1.3
解：当负载（与接收自整角机 TR 的转子固联)的角位置 o 与发送机 Tx 转子的输入角位置 6
一致时，系统处于相对豫止状态，自整角机输出电压(即偏差电压)为 0，放大器输出为 0，
电动机不动，系统保持在平衡状态。当 i 改变时， o 与 i 失谐，自整角接收机输出与失谐
角成比例的偏差电压，该偏差电压经整流放大器、功率放大器放大后驱动电动机转动，带动
减速器改变负载的角位置 o ，使之跟随 i 变化，直到与 i 一致，系统达到新的平衡状态时
为止。系统中采用测速发电机 TG 作为校正元件，构成内环反馈，用于改善系统动态特性。
该系统为随动系统。被控对象是负载；被控量为负载角位置 o ，给定量是发送自整角
机 TX 转子的角位置 i 。自整角机完成测量、比较元件的功能，整流放大器、功率放大器共
同完成放大元件的功能，电动机 SM 和减速器组成执行机构，测速发电机 TG 是校正元件，
系统方框图如图解 1.4.6 所示。
1.4
解 工作原理：温度传感器不断测量交换器出口处的实际水温，并在温度控制器中与给定温
度相比较，若低于给定温度，其偏差值使蒸汽阀门开大，进入热交换器的蒸汽量加大，热水
温度升高，直至偏差为零。如果由于某种原因，冷水流量加大，则流量值由流量计测得，通
过温度控制器，开大阀门，使蒸汽量增加，提前进行控制，实现按冷水流量进行前馈补偿，
保证热交换器出口的水温波动不大。
系统中，热交换器是被控对象，实际热物料温度为被控变量，冷水流量是干扰量。
系统方框图如图解 1.4.4 所示。
这是一个按干扰补偿的复合控制系统。
1.5
解 带上负载后，由于负载的影响，图(a)与图(b)中的发电机端电压开始时都要下降，但图(a)
中所示系统的电压能恢复到 110 v，而图(b)中的系统却不能。理由如下；
对图(a)所示系统，当输出电压 u 低于给定电压时，其偏差电压经放大器 K，使电机 SM
转动，经减速器带动电刷减小发电机 G 的激磁回路电阻，使发电的激磁电流 fi 增大，提高
发电机的端电压，从而使偏差电压减小，直至偏差电压为零时，电机才停止转动。因此，图
(a)系统能保持 110V 电压不变。
对图(b)所示系统，当输出电压u 低于给定电压时，其偏差电压经放大器 K，直接使发
电机激磁电流 fi 增大，提高发电机的端电压，使发电机 G 的端电压回升，偏差电压减小，
但是偏差电压始终不可能等于零，因为当偏差电压为零时，
fi ，发电机就不能工作。偏
差电压的存在是图(b)系统正常工作的前提条件。即图(b)中系统的输出电压会低于 110V。
0
第二章
2.1
(a)
m
2
d x
o
2
dt
(
f
1
f
2
)
dx
o
dt
f
1
dx
i
dt
(不考虑物块的重力)
)
2
(
f K K
1
dx
o
dt
(
f
dx
o
dt
)
K K x
1
f
o
2
K K x
2
1
K f
1
dx
i
dt
K x
1
i
o
dx
i
dt
(b)
(c)
2.2
(a)
o
( )
U s
( )
U s
i
R
2
R
2
1
C s
2
R
1
1
C s R
2
1
1
C s
1
1
C s
1
2
R R C C s
2
1
(
1
R R C C s
1
2
1
)
R C R C R C s
1
(
)
R C R C s
1
2
2
1
2
2
2
1
1
2
2
1
2
1
)
(
K x
2
i
x
)
o
f
1
(
dx
o
dt
dx
)
dt
（1）
K x
1
（2）
f
(b) A 点： 2
dx
(
i
dt
odx
dt
dx
o
dt
dx
)
f
B 点： 1
dt
由（1）和（2）得
f
(
(
)
dx
o
dt
dx
i
dt
i
o
2
2
)
x
(
K x
K x
1
由（3）解出 x ，并代入（2）得：
2
dx
d x
f
f f
2
1 2
o
o
2
K dt
K K dt
1
f
1
K
1
f
1
K
(
)
2
2
2
（3）
x
o
2
d x
f f
1 2
i
2
K K dt
1
2
(
f
1
K
1
dx
f
2
i
K dt
)
2
x
i
经比较可以看出，电网络（a）和机械系统(b)两者参数的相似关系为
K
1
~
1
C
1
,
K
1
~
1
C
1
,
f
1
~
R
1
,
f
2
~
R
2
2.3
Q
K
P
0
2
P
2.4
( )
G s
2
2
s
s
4
s
3
s
2
2
( )
g t
L
1
[1
1
1
s
2
s
2
]
( )
t
e
t
2
e
2
t
2.5
h
1
h
2
R
1
d h
1
dt
C
1
h
2
R
2
q
1
(1)
q
1
q
i
(2)
q
2
(3)
C
2
d h
2
dt
q
q
1
2
(4)
( )
G s
( )
H s
2
( )
Q s
i
2.6
R C R C s
1
2
1
2
2
(
R
2
)
R C R C R C s
1
1
2
2
1
2
1
( )
G s
( )
C s
( )
E s
10
3
s
5
( )
H s
2
s
4
1
10 ( )
G s
( )
( )
G s H s
1
1)
100(4
s
23
25
s
s
2
12
10
( )
( )
G s H s
2
10(12
s
2
12
s
23
s
23
s
5)
25
1
( )
C s
( )
R s
( )
E s
( )
R s
2.7
o
( )
U s
( )
U s
i
R
1
1
C s
1
1
C s
0
1
C s
0
R
0
R
0
R C R C s
0
1
0
1
2
)
(
R C R C s
0
1
R C s
1
0
1
0
1
K
2.8 （1） 0
E
m
30
180
330
180
11
V rad
/
K
1
3,
K
2
2
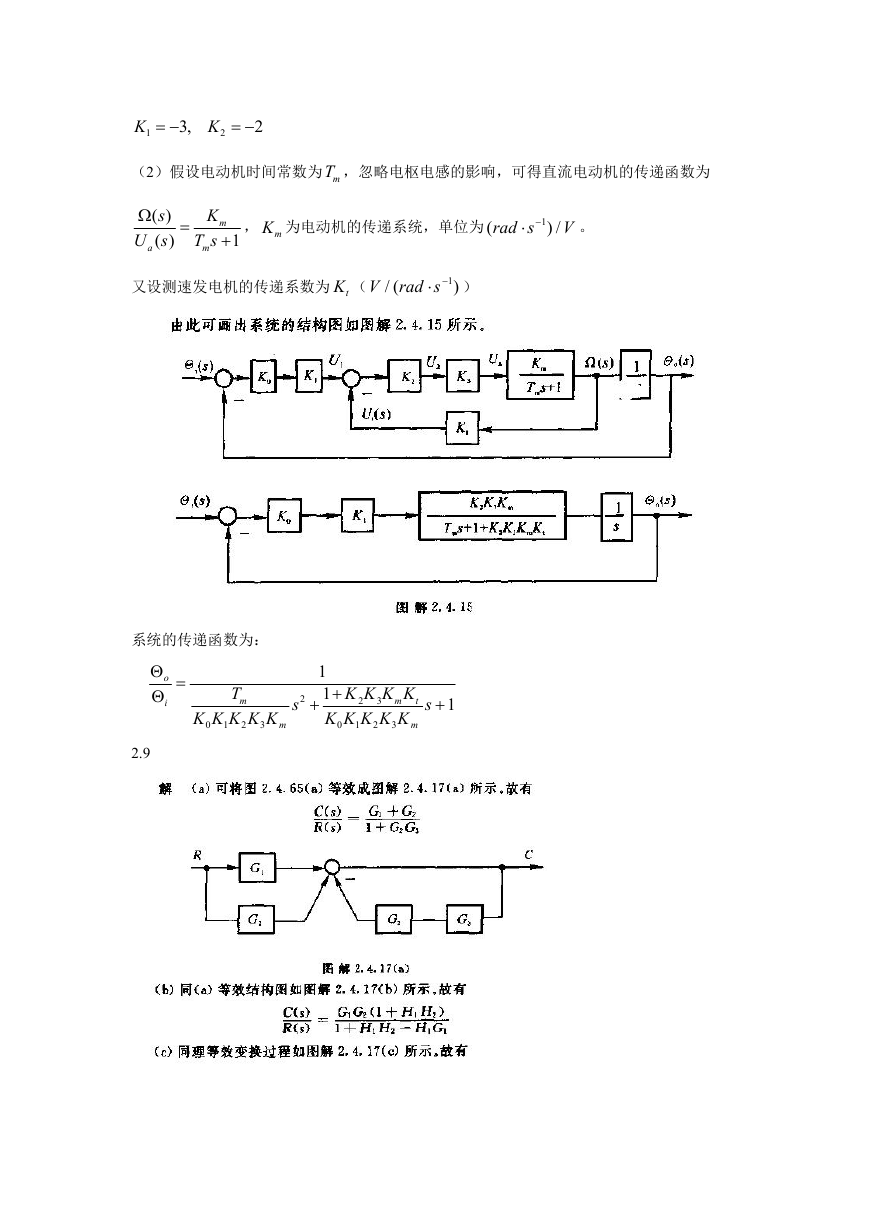
（2）假设电动机时间常数为 mT ，忽略电枢电感的影响，可得直流电动机的传递函数为
( )
s
( )
U s
a
K
T s
m
m
1
， mK 为电动机的传递系统，单位为
(
rad s
1
) /
V
。
V rad s ）
/ (
)
1
又设测速发电机的传递系数为 tK （
系统的传递函数为：
o
i
2.9
T
m
K K K K K
0
1
2
3
2
s
m
1
1
K K K K
m t
K K K K K
2
3
m
0
1
2
3
s
1
相关推荐
2023年江西萍乡中考道德与法治真题及答案.doc
2012年重庆南川中考生物真题及答案.doc
2013年江西师范大学地理学综合及文艺理论基础考研真题.doc
2020年四川甘孜小升初语文真题及答案I卷.doc
2020年注册岩土工程师专业基础考试真题及答案.doc
2023-2024学年福建省厦门市九年级上学期数学月考试题及答案.doc
2021-2022学年辽宁省沈阳市大东区九年级上学期语文期末试题及答案.doc
2022-2023学年北京东城区初三第一学期物理期末试卷及答案.doc
2018上半年江西教师资格初中地理学科知识与教学能力真题及答案.doc
2012年河北国家公务员申论考试真题及答案-省级.doc
2020-2021学年江苏省扬州市江都区邵樊片九年级上学期数学第一次质量检测试题及答案.doc
2022下半年黑龙江教师资格证中学综合素质真题及答案.doc
