第1页 / 共223页
第2页 / 共223页
第3页 / 共223页
第4页 / 共223页
第5页 / 共223页
第6页 / 共223页
第7页 / 共223页
第8页 / 共223页
信号与系统(第二版)余成波主编清华大学出版社课后习题答案.pdf
http://www.benxiao.com
第一章 信号与系统的基本概念
1．1 学习重点
1、 信号与系统的基本概念，信号的分类，会画信号的波形。
2、 常用基本信号（连续时间信号和离散时间信号）的时域描述方法、 特点以及性质，
并会灵活运用性质。
3、 信号的时域分解、 变换与时域运算，及其综合运用。
4、 深刻理解线性时不变系统的定义与性质，并会应用这些性质。
5、 利用MATLAB 表示信号、 实现信号的基本运算。
1．2 教材习题同步解析
1.1 下列信号中哪些是周期信号，哪些是脉冲信号？哪些是能量信号，它们的能量各为多少？哪些
是功率信号，它们的平均功率各为多少？
（2） ( )
（1） ( )te
t
( )t
1
e+1
t
(
)qw +0
3 je
（4）
（6）
（3）
（5）
e at
e
(
t
e
(
w +t0
)1-
)q
( )t
cos
ew 0
t
cos3
（7） ( )t
te3
（8）
cos
t
w +
0
4
sin
t
w
0
5
【 知识点窍】 本题考察周期信号、 脉冲信号、 能量信号、 功率信号的概念
【 逻辑推理】 时间间隔无穷大时，周期信号都是功率信号，只存在有限时间内的信号是能量信
号。信号总能量为有限值而信号平均功率为零的是能量信号；信号平均功率为有限值而信号总能量
为无限大的是功率信号。
解：（1） ( )te 是功率信号，其平均功率：
1
-
-
=
P
lim
T
1
T
2
T
T
[
e
]
( )
t
2
=
dt
1
2
¥=E
（2） ( )
t
e
(
t
)1-
e
E
0=P
是脉冲信号，其为能量信号，能量为：
( )
t
]
)
1
( )
t
[
e
[
e
(
t
dt
=
=
e
2
lim
T
T
T
1
0
(
t
e
]
)
1
2
dt
=
1
（3）
( )t
1
e+1
t
是能量信号，其能量为：
=
E
lim
T
T
T
1
+
t
1
( )
t
e
2
=
dt
1
+
t
1
0
2
( )
t
e
dt
=
1
=
P
lim
T
1
2
T
T
T
1
+
t
1
2
( )
t
e
=
dt
0
（4）
cos3
(
w +t0
)q
是功率信号，其平均功率为：
=
P
lim
T
1
2
T
T
T
[
cos3
(
w
0
t
]
)
2
+
q
=
dt
lim
T
=
E
lim
T
T
T
[
(
w
cos3
+
q
t
0
1
2
T
]
)
2
dt
（5）
3 je
(
)qw +0
为功率信号，其平均功率为：
+
q
)
+
1
cos
(
w
t
2
0
2
=
dt
lim
T
1
2
T
9
2
=
2
T
9
2
[
cos3
(
w
+
q
t
0
]
)
2
¥=
dt
T
T
9
=
29 je
(
)qw +
0
P
(
+
qw
0
j
[
3
e
T
T
=
E
lim
T
=
]
)
2
=
dt
lim
T
9
e
(
+
qw
0
)
2
j
¥=
T
2
（6）
e at
cos
ew 0
t
( )t
为能量信号，其能量为：
=
E
lim
T
[
e
T
T
at
cos
=
lim
T
T
0
e
2
at
0
]
( )
ew
t
t
w
2cos
t
2
0
2
dt
+
1
=
dt
lim
T
=
1
4
a
T
0
e
2
at
2
cos
w
0
dtt
+
14
a
1
2
0
2
w
a
0=P
（7） ( )t
te3
既非能量信号又非功率信号，因其：
[
t
3
P
=
T
lim
T
1
T
2
T
]
( )
t
2
e
¥=
dt
2
-
¥
fi
-
-
-
-
-
-
¥
fi
¥
-
¥
fi
œ
ß
ø
Œ
º
Ø
œ
ß
ø
Œ
º
Ø
œ
ß
ø
Œ
º
Ø
-
¥
fi
¥
fi
-
¥
fi
-
¥
fi
¥
¥
-
-
¥
fi
¥
fi
-
¥
fi
-
ł
Ł
-
-
¥
fi
-
¥
fi
-
-
¥
fi
-
¥
fi
=
E
lim
T
T
T
[
e
t
3
]
( )
t
2
=
dt
0
[
3
t
e
]
( )
t
2
¥=
dt
（8）
cos
t
w +
0
4
sin
t
w
0
5
为功率信号，其平均功率为
=
P
lim
T
1
2
T
T
T
cos
t
w
0
4
+
sin
t
w
0
5
2
dt
1
2
T
1
2
T
T
T
T
T
2
cos
t
w
0
4
+
2
cos
t
w
0
4
sin
t
w
0
5
+
2
sin
t
w
0
5
dt
+
1
t
+
sin
cos
w
0
2
t
w
9
0
20
sin
+
w
t
0
20
1
cos
2
t
0
w
2
5
dt
1
2
T
1
2
+
2
T
1
2
T
1
2
2
T
=
lim
T
=
lim
T
=
=
lim
T
1
¥=E
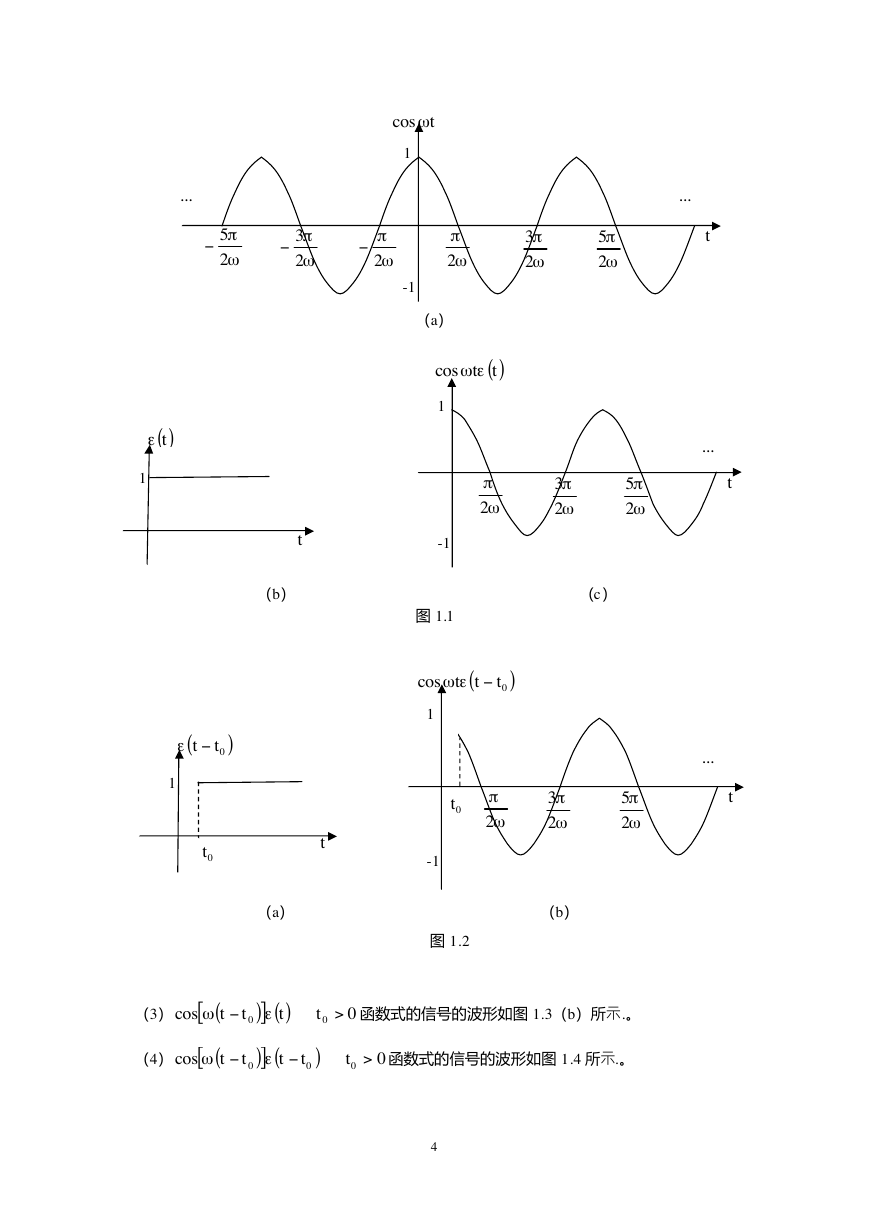
1.2 试画出下列各函数式表示的信号的波形。
( )t
（1）
tewcos
(
t
)
[
w
cos
（3）
（5） (
te
（7） (
e
t
2
t
[ ]nn e-2
（9）
t
0
0
0
t
0
t
0
>
（2）
] ( )
)
e
t
tew
cos
[
(
w
cos
t
（4）
（6） (
te
（8） [
e sin
t
0
(
e
>
0
t
0
)
2
t
>
0
)
t
0
（10）
(
t
0
)
t
] (
)
e
t
t
0
>
0
t
0
)
t
0
>
0
t
0
)
2
t
]tp
) [
e
n
2
0
(
n
2
>
0
t
0
]2
（11）
[
nne
]2+
（12）
sin
1
5
np
【知识点窍】本题考察基本信号的绘制及自变量变换导致信号变换的概念
【逻辑推理】本题用到了基本信号的性质及信号的时域运算与变换。
解：
（1）
tewcos
（2）
cos
tew
( )t
(
t
函数式的信号的波形如图 1.1（c）所示.。
)
t
0
>
0
t
0
函数式的信号的波形如图 1.2（b）所示.。
3
¥
-
¥
fi
œ
ß
ø
Œ
º
Ø
œ
œ
œ
œ
ß
ø
Œ
Œ
Œ
Œ
º
Ø
-
-
œ
ß
ø
Œ
º
Ø
œ
ß
ø
Œ
º
Ø
¥
fi
-
¥
fi
-
¥
fi
-
¥
fi
-
-
-
-
-
-
-
-
-
-
-
-
-
-
ł
Ł
-
…
p
5-
w
2
p
3-
w
2
( )te
1
t
twcos
1
p
w
2
p
3
w
2
p
5
w
2
p
w
2
-1
（a）
tewcos
( )t
1
-1
p
w
2
p
3
w
2
p
5
w
2
…
t
…
t
（b） （c）
图 1.1
cos
ew
t
(
t
)
t
0
(
t -
e
)
0t
1
0t
t
1
-1
0t
p
w
2
p
3
w
2
p
5
w
2
…
t
（a） （b）
图 1.2
[
w
cos
[
w
cos
(
t
(
t
（3）
（4）
] ( )
)
e
t
] (
)
e
t
t
0
t
0
t
)
t
0
>
0
0
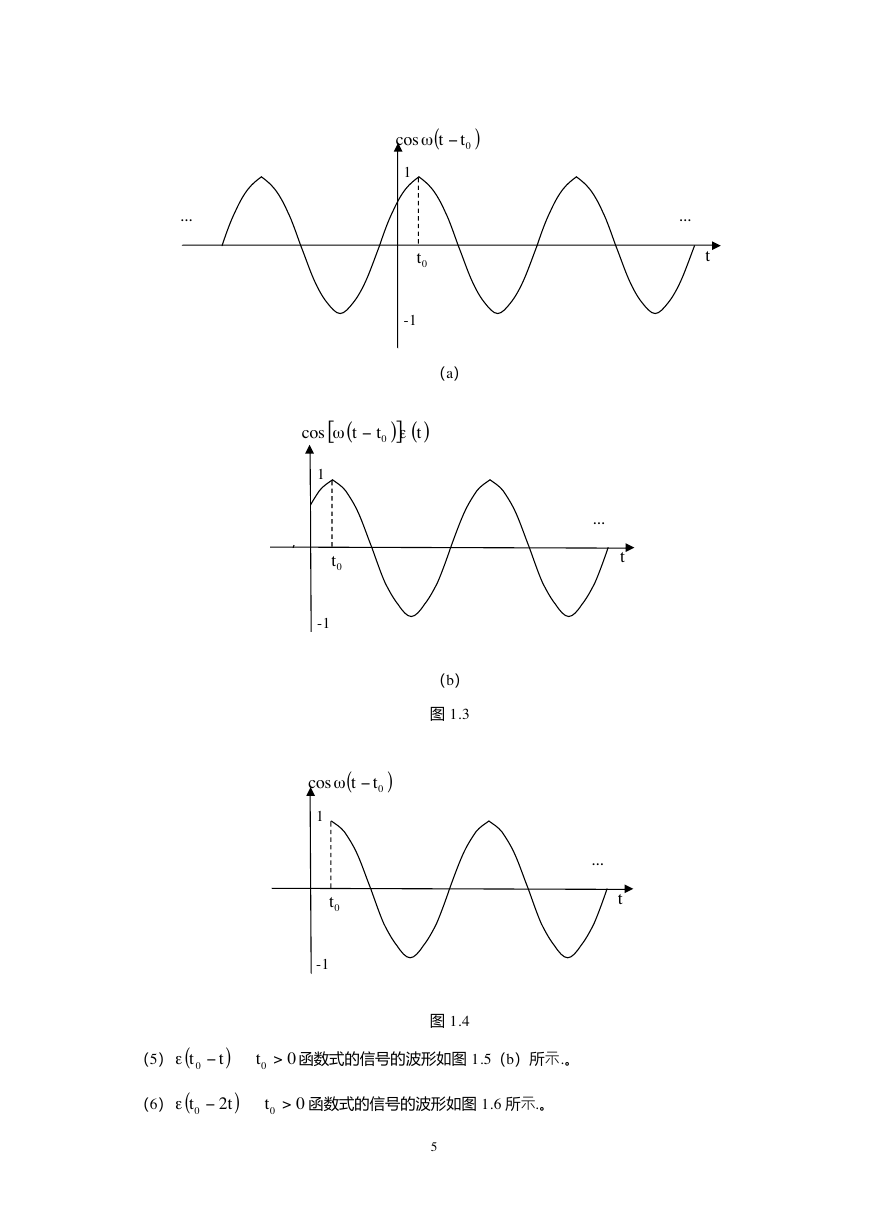
函数式的信号的波形如图 1.3（b）所示.。
>
0
t
0
函数式的信号的波形如图 1.4 所示.。
4
-
-
-
-
-
…
(
t -w
cos
)
t
0
1
0t
-1
（a）
[
w
(
t
cos
] ( )t
)
e
t
0
（b）
图 1.3
1
0t
-1
(
t -w
cos
)
t
0
1
0t
-1
…
t
…
t
…
t
图 1.4
（5） (
te
（6） (
te
0
0
)
t
)
2
t
>
0
t
0
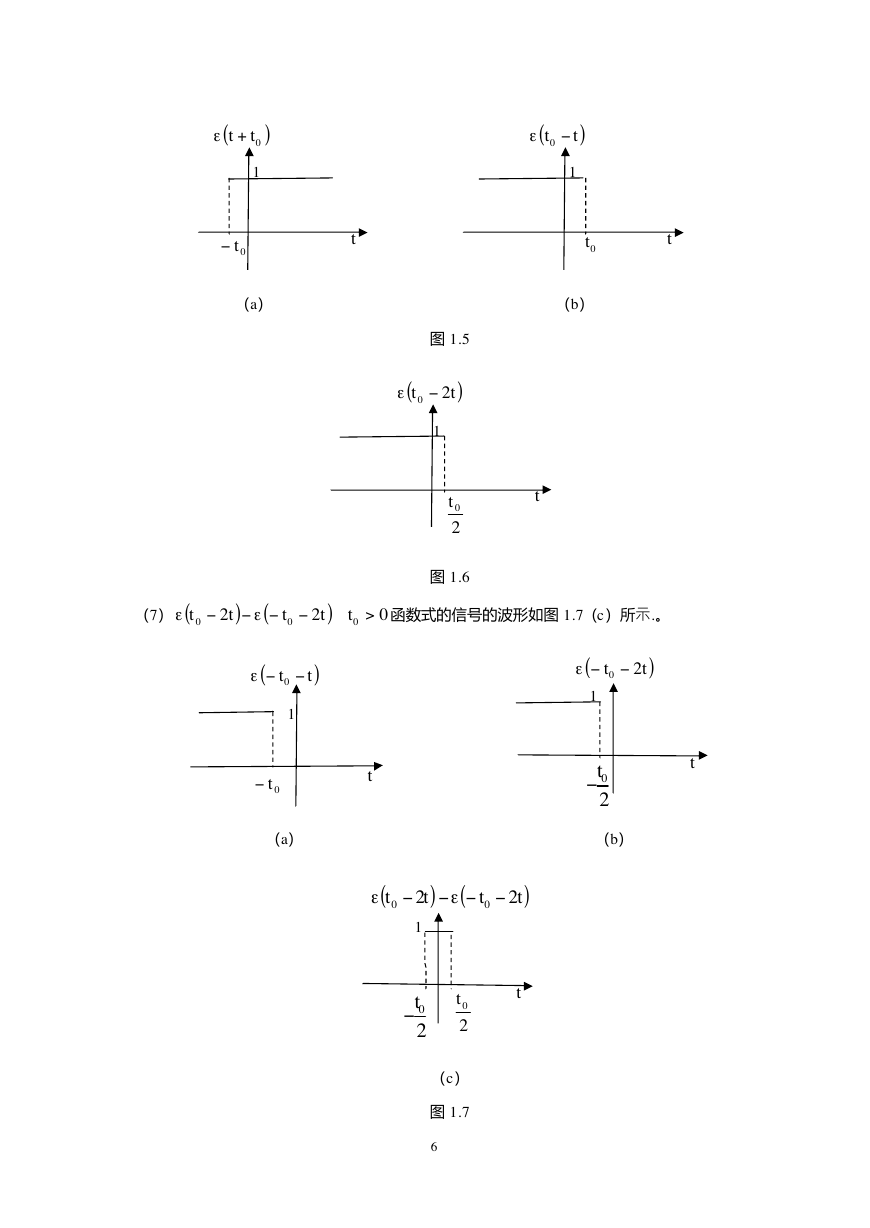
函数式的信号的波形如图 1.5（b）所示.。
>
0
t
0
函数式的信号的波形如图 1.6 所示.。
5
-
-
-
(
t +e
)
0t
1
(
0e
t
)t
1
0t
t
0t
t
（a） （b）
图 1.5
(
t
e
0
)t
2
1
0t
2
图 1.6
t
（7） (
e
t
0
)
2
t
(
e
t
0
)
2
t
>
0
t
0
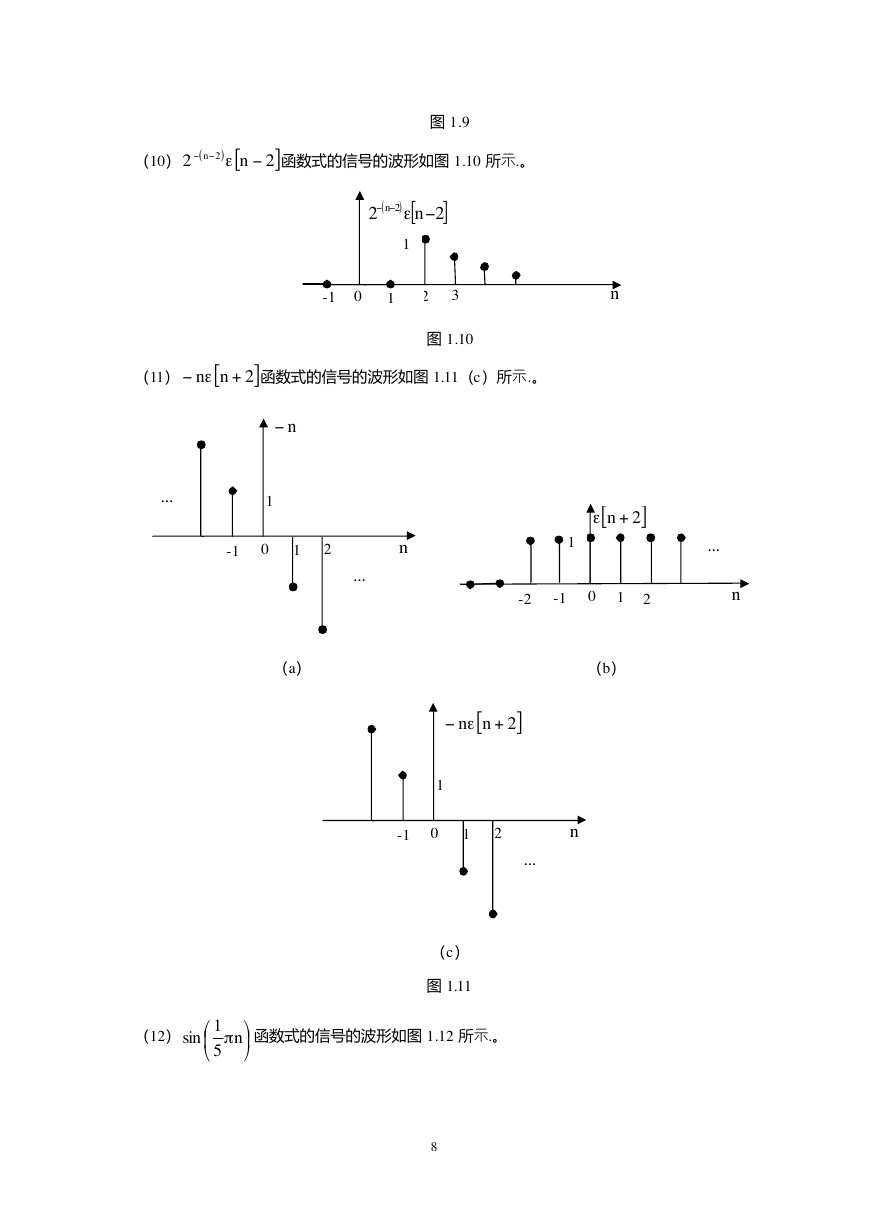
函数式的信号的波形如图 1.7（c）所示.。
(
e
t
0
)t
1
0t
)t
2
t
0
(
-e
1
t
0t-
2
t
（a） （b）
(
t
e
0
)
t
2
1
(
e
t
0
)t
2
t
0t-
2
0t
2
（c）
图 1.7
6
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
（8） [
]tp
e sin 函数式的信号的波形如图 1.8（b）所示.。
tpsin
1
-2
-1
1
2
3
-1
（a）
[
e sin
]tp
1
…
…
-2
-1
1
2
3
[ ]nn e-2
（9）
函数式的信号的波形如图 1.9（c）所示.。
（b）
图 1.8
…
t
…
t
[ ]ne
1
-1
0
1
2
n-2
…
1
n
-1
0
1
2
…
n
（a） （b）
[ ]nn e-2
1
-1
0
1
2
（c）
7
…
n
（10）
2
(
n
) [
e
n
2
]2
函数式的信号的波形如图 1.10 所示.。
图 1.9
]2
(
) [
n e
2 2
n
1
-1
0
1
2
3
图 1.10
…
n
（11）
[
nne
]2+
函数式的信号的波形如图 1.11（c）所示.。
n-
…
1
-1
0
1
2
n
…
[
]2+ne
1
-2
-1
0
1
2
（a） （b）
…
n
[
nne
]2+
1
-1
0
1
2
n
…
（c）
图 1.11
（12）
sin
1
5
np
函数式的信号的波形如图 1.12 所示.。
8
-
-
-
-
ł
Ł
-
-
-
-
相关推荐
2023年江西萍乡中考道德与法治真题及答案.doc
2012年重庆南川中考生物真题及答案.doc
2013年江西师范大学地理学综合及文艺理论基础考研真题.doc
2020年四川甘孜小升初语文真题及答案I卷.doc
2020年注册岩土工程师专业基础考试真题及答案.doc
2023-2024学年福建省厦门市九年级上学期数学月考试题及答案.doc
2021-2022学年辽宁省沈阳市大东区九年级上学期语文期末试题及答案.doc
2022-2023学年北京东城区初三第一学期物理期末试卷及答案.doc
2018上半年江西教师资格初中地理学科知识与教学能力真题及答案.doc
2012年河北国家公务员申论考试真题及答案-省级.doc
2020-2021学年江苏省扬州市江都区邵樊片九年级上学期数学第一次质量检测试题及答案.doc
2022下半年黑龙江教师资格证中学综合素质真题及答案.doc
