一种三自由度并联机构的构型与运动学分析.pdf-资料库

一种三自由度并联机构的构型与运动学分析 http://www.paper.edu.cn 郑建勇 1 ，李为民 2，史金飞 1 1.东南大学机械工程学院，南京（211189） 2.河北工业大学机械学院，天津（300130） E-mail：zjy_207@163.com 摘要：文中从运动副分析入手，对一种运动解耦的三自由度并联机构进行了构型研究，该机构由三个正交分布的支链组成，且机构的运动副均为转动副，构成了机构动平台 X、 Y、Z 三个方向的平动解耦；在机构构型研究的基础上，对其进行了运动学分析，推导出了该并联机构的运动学正反解，分析了机构输入/输出的速度和加速度等，验证了该机构运动解耦的特性。这对该机构的动力学分析、控制策略、机构设计和轨迹规划等方面的研究，具有一定的理论意义。关键词：三自由度并联机构，构型，运动学，解耦中图分类号：TP242.2 1 引言目前，具有六自由度的并联机器人得到了广泛的研究，然而许多场合需要期望输出运动为常量的少自由度的并联机器人，其中三自由度并联机器人是并联机构中一种很有实用前景的机器人，它也是随着机器人技术的发展而发展起来的[1]。Lee 和 Shah 研究了空间三自由度并联机器人的设计[2]；金琼和杨廷力等[3-4]分析了一类新型三平移解耦并联机构；李惠良等[5] 基于机构结构组成理论，综合出了一类完全解耦的一平移两转动的 3 自由度并联机构；杭鲁滨等[6]基于解耦判定准则，构造了一种新型的三平移一转动解耦并联机构，该机构既具有拓扑解耦特性，又具有尺度解耦特性；Weimin Li[7-8]提出了一种完全解耦的三自由度移动并联机构。运动解耦的并联机构容易控制，而且可以达到很高的精度[9]。文中对这种三自由度并联机构进行了构型分析，建立该机构的运动学模型，验证了该机构具有运动解耦的特性，为该并联机构的动力学分析、有效控制和推广应用等方面提供了一定的理论基础。 2 构型形式及特点平动并联机构的解耦构型研究的基本思想是：一个直线运动输入与垂直于该输入的平面上的运动无关。其物理意义如图 1 所示。图中，移动副 P 作为输入确定平面副在 z 坐标轴方向的位置，而平面副 F 沿 x、y 方向的运动与移动副 P 的输入无关。因此，用图 1（a）所示运动简图作为支链（PF），可以组成输入输出一一对应运动解耦平动并联机构。通过对移动副 P 和平面副 F 的进行构型综合研究，可以设计出运动解耦三自由度平动并联机构的各种类型。平面副可以有各种构型，图 1（b）给出了 3 种典型的构型形式：RRR、 PPR 和 RPR（其中 R 表示转动副，P 表示移动副）。图 1（c）给出了移动副 P 的一种替代形式，由 4 个转动副组成。将平面副 F 和移动副 P 进行不同的组合，可以组成并联机构不同的支链形式，如图 2 所示。 - 1 -

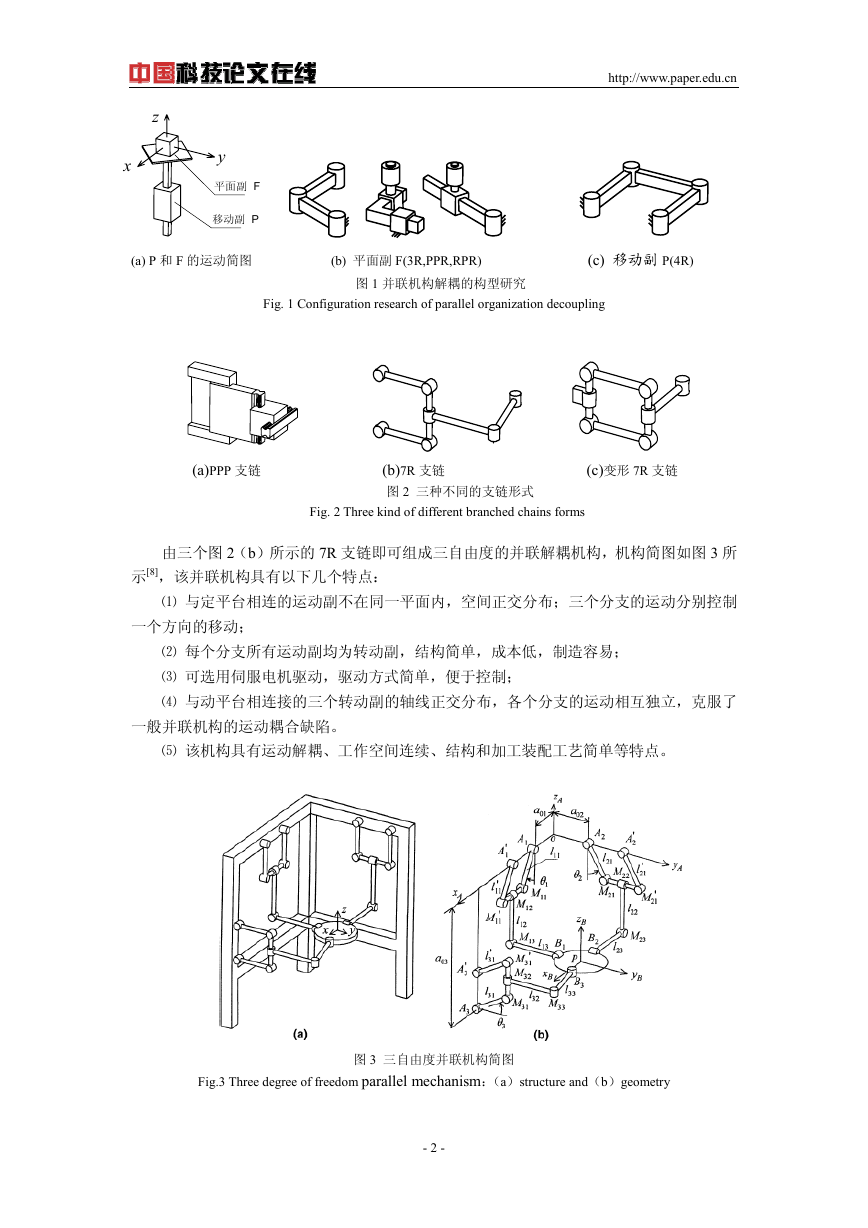
http://www.paper.edu.cn z x y 平面副 F 移动副 P (a) P 和 F 的运动简图 (b) 平面副 F(3R,PPR,RPR) (c) 移动副 P(4R) 图 1 并联机构解耦的构型研究 Fig. 1 Configuration research of parallel organization decoupling (a)PPP 支链 (b)7R 支链图 2 三种不同的支链形式 (c)变形 7R 支链 Fig. 2 Three kind of different branched chains forms 由三个图 2（b）所示的 7R 支链即可组成三自由度的并联解耦机构，机构简图如图 3 所示[8]，该并联机构具有以下几个特点： ⑴ 与定平台相连的运动副不在同一平面内，空间正交分布；三个分支的运动分别控制一个方向的移动； ⑵ 每个分支所有运动副均为转动副，结构简单，成本低，制造容易； ⑶ 可选用伺服电机驱动，驱动方式简单，便于控制； ⑷ 与动平台相连接的三个转动副的轴线正交分布，各个分支的运动相互独立，克服了一般并联机构的运动耦合缺陷。 ⑸ 该机构具有运动解耦、工作空间连续、结构和加工装配工艺简单等特点。 Fig.3 Three degree of freedom parallel mechanism：（a）structure and（b）geometry 图 3 三自由度并联机构简图 - 2 -

3 坐标系的建立如图 3 所示，将固定坐标系 o-xAyAzA 设定在机架的左上方，动坐标系 P-xByBzB 设置在 http://www.paper.edu.cn 动平台的几何中心上。其中， =im i (0 )3,2,1 代表设定参见图 3 所示。 =iMM i (' 1 i 1 )3,2,1 的杆长，其余各参数的该并联机构动平台上的三个转动副的坐标如下： ⎤ ⎥ ⎥ ⎥ ⎦ a + 01 l sin β + 1 13 l cos β + 12 1 l 12 cos θ 1 B1： + ) ) ' 1 m l + 11 01 cos( ' ββ + 1 1 l sin( ββ + 13 1 cos( ' ββ 2 + θ 2 + + 2 m 02 sin( l 23 sin β 2 23 ) l ' ββ 2 + 2 ) l 22 sin a 02 l + + β 2 l + 21 cos 22 cos θ 2 l a [ − 04 cos θ 3 − sin l β 3 cos 32 l + 31 03 l + β 3 sin cos( 33 l + θ 3 33 + )] ' + ββ 3 3 sin( ' + ββ 3 m 03 3 ) 32 + a 31 ⎡ ⎢ ⎢ l ⎢ ⎣ 11 ⎡ ⎢ ⎢ ⎢ l ⎣ ⎡ ⎢ l ⎢ ⎢ ⎣ 21 B2： B3： = ⎡ ⎢ Y ⎢ ⎢ ⎣ P − r X P Z P X ⎤ ⎥ ⎥ ⎥ ⎦ − （1） r ⎤ ⎥ ⎥ ⎥ ⎦ （2） P Y Z P P + r P P P Y Z ⎤ ⎥ ⎥ ⎥ ⎦ （3） ⎤ ⎥ ⎥ ⎥ ⎦ ⎤ ⎥ ⎥ ⎥ ⎦ = = ⎡ ⎢ ⎢ ⎢ ⎣ X ⎡ ⎢ ⎢ ⎢ ⎣ 4 运动学分析 4.1 并联机构运动学的逆解分析运动学逆解即运动学的逆问题，是当并联机器人的结构参数和动平台参考点 P 的位置（XP、YP、ZP）已知时，求各个分支输入运动副摆角 ( =iiθ )3,2,1 的大小。 ( =iiθ )3,2,1 1. 求解输入变量 m a X arcsin(( − − m a Y arcsin(( − − 02 02 m a Z arcsin(( − + = = = θ 1 θ 2 θ 3 03 01 P P P /) 01 /) /) 03 （4） l 11 l 21 l 31 ) ) ) 2. 求解中间变量 =β 1 arctan [ （、、、、、 1 UV − ' ββββββ 3 3 UD )( ' 1 VU 2 ' 2 V ( − − ± 2 2 2 2 2 − 2 D U /(]) 2 − 2 D ) ）（5） ' β 1 （6） = arctan(( Z − l 11 cos θ 1 − l 12 cos β 1 Y /() P −− r l 12 sin P ββ 1 − )) 1 =β 2 arctan [ （ VU ' − ' ± 2' VU 2' − V ( 2' 2' UD )( − 2' 2' − D U /(]) 2' 2' − D ) ）（7） ' β 2 （8） = arctan(( Z − l 21 cos θ 2 − l 22 cos β 2 /() X P P −− r l 22 sin ββ 2 − )) 2 =β 3 arctan [ （ VU '' − '' ± 2'' VU 2'' − V ( 2'' 2'' UD )( − 2'' 2'' − D U /(]) 2'' 2'' − D ) ）（9） - 3 -

' β 3 = Y arctan(( − l 31 cos θ 3 − l 32 cos β 3 /() a 04 − X P P −− r l 32 sin http://www.paper.edu.cn 3 )) − ββ 3 （1 0） ' 2 2 21 − + Z P + − l 2 32 − P l − Y ( + l ) 2 l 2 12 2 − 22 l + l 11 cos l − ) ( + Z ( + r ) 2 cos ) θ 1 ) 2 θ 2 cos l l 2/] 2 13 12 l 2/) 2 ， 23 22 l l 2/) 2 − 33 YU r = P − ，， r X U =' P − Y r [( − 其中：D= P r X D (( ) 2 = − a D X (( '' = X a r = 04 − V Z cosθ ； P − = 3 综上分析，当动平台参考点 P 的位置（ PX 、 PY 、 PZ ）已知， 1 θθθ 、、 2 3 ′ 、、 ′ βββ 3 1 P − P 04 P − ， l 11 cosθ 1 βββ 、、 3 均有 2 个解，的解分别与 cosθ 2 均有唯一 P − P − θ 3 ， ,， V V ，， Z Y = = 21 31 32 31 ′ 2 1 2 l l P '' ' 解，即运动学的逆解唯一。而中间变量 '' U βββ 、、 3 2 1 有关。 4.2 并联机构运动学的正解分析位置正解是当机器人的结构参数和输入运动副的角位移( )3 θθθ 、、 1 2 已知时，求并联机器人动平台参考点 P 点在固定坐标系中的位置（XP、YP、ZP）。 1. 求解输出参数（XP、YP、ZP） P 01 X Y Z a = a = 02 a −= m l sin + + θ 1 11 m l sin + θ + 2 02 m sin + θ + 3 2. 求解中间变量 21 l 31 03 P P 01 03 （11）参照求逆解的方法可分别求出运动学正解的中间变量 ' ββββββ 3 ' 2 ' 1 , , , , , 3 2 1 ，但求解过程要比求逆解中间变量的过程复杂，这与串联机器人正解容易、逆解困难的特点相反。 4.3 并联机构的速度和加速度分析由于上平台为刚体，所以上平台上各点的线速度都相等，各点的线加速度也都相等。将 XP、YP、ZP 对时间求一阶导数，得到动平台的速度，即该并联机构的速度正/反解如下： ( Z Y X &= & & p p V p )T p • 1θ − = J ， • X P ⎡ ⎢⎣ • Y P • Z P T ⎤ ⎥⎦ （12）其中： • • • θθθθ 3 2 1 • ⎡= ⎢⎣ T ⎤ ⎥⎦ ，[ ] J 1 =− l 11 1 cos 0 θ 1 0 0 1 cos 0 θ 2 l 21 ⎡ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎣ （13） ⎤ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎦ 0 0 1 cos }P l 31 Z && θ 3 如果已知动平台参考点 P 的加速度 Pa 的分量{ X && ，， P Y && P 、机构尺寸参数、各个驱动副的角度以及角速度，就可得到角加速度 •• θ的各个分量： - 4 -

= ⎞ ⎟ ⎟ ⎟ ⎟⎟ ⎠ ⎞ ⎟ ⎟ ⎟ ⎠ − ⎡ ⎢ ⎢ ⎢ ⎣ ⎛ ⎜ ⎜ ⎜ ⎜ ⎜⎜ ⎝ ⎛ ⎜ ⎜ ⎜ ⎝ 1 − [ ] J P X && Y && P Z && P ⎛ •• θ ⎜ 1 ⎜ •• θ 2 ⎜ •• ⎜⎜ θ 3 ⎝ l 0 0 sin − θ 11 1 l sin 0 0 − θ 2 l sin 0 − ⎛ • 2 ⎜ θ 1 ⎜ • 2 θ ⎜ 2 ⎜ • 2 θ ⎜ 3 ⎝ 根据方程（1）～（14）的推导，可得出以下的结论： 1）该三自由度并联机构的运动雅克比矩阵为对角阵，只跟其每个分支的驱动杆的长度（14） ⎞ ⎟ ⎟ ⎟ ⎟ ⎟ ⎠ ⎞ ⎟ ⎟ ⎟ ⎟ ⎟⎟ ⎠ 31 θ 3 21 0 http://www.paper.edu.cn ⎤ ⎥ ⎥ ⎥ ⎦ 以及各个分支的输入角 iθ有关，与其它参数无关； 2）机构每个分支的运动只引起动平台参考点一个坐标量的变化，对其他两个坐标分量没有影响； 3）运动雅克比矩阵动平台参考点的坐标只跟三个分支驱动杆的长度、三个分支的安装位置尺寸以及输入角有关系，与其它参数无关； 4）动平台参考点的速度只跟三个分支驱动杆的长度、驱动角速度以及输入角有关，而与其它参数无关。故而，该机构具有运动解耦的特性。 5. 结论文中从运动副分析入手，对一种具有 X、Y、Z 三个方向平动解耦的并联机构进行了构型分析，并根据机构的特点对其进行了运动学研究，分析了机构的正反解、速度和加速度等，建立了运动学模型。结果验证了该并联机构具有运动解耦的特性，这对并联机构的动力学研究、机构设计、轨迹规划和提高加工质量等都有重要的理论意义。参考文献 [1] 晁艳霞. 解耦结构三平移力反馈控制器研究[D].天津，河北工业大学，2004. [2] Gosselin C M. On the development of reactionless spatial 3 – DOF parallelpiped mechanisms [J] . Proc. of DECT’02 ASME 2002 Design Engineering Technical Conferences. September 29-October 2. Montreal , Canada ,2002. [3] 金琼，杨廷力. 一类新型三平移并联机器人机构的位置分析[J].东南大学学报(自然科学版)，2001，31 (5)： 33-38. [4] Jin Qiong, Yang Tingli. Synthesis and analysis of a group of 3-degree-of-freedom partially decoupled parallel manipulators [J]. Journal of Mechanical Design , 2004 , 126 : 301-306. [5] 李惠良，金琼，杨廷力.一类一平移两转动解耦并联机构及其位移分析[J].机械制造与研究，2002(1)： 9-14. [6] 杭鲁滨，王彦，杨廷力.一种新型三平移一转动解耦并联机构分析[J].中国机械工程，2004，15(12)： 1035-1037，1041. [7] Li Weimin, Gao Feng, Zhang Jianjun. A three-DOF translational manipulator with decoupled geometry [J]. Robotica , 2005 ,23 :805-808. [8] Li Weimin , Gao Feng , Zhang J ianjun. R-CUBE , a decoupled parallel manipulator only with revolute joints[J]. Mechanism and Machine Theory, 2005 , 40 :467-473. [9] 曲云霞，李为民，范顺成等. 并联机构构型研究概述[J]. 新技术新工艺，2007，第 2 期：48-51. - 5 -

The Configuration and Kinematics Analysis of a Three Degree of Freedom Parallel Mechanism http://www.paper.edu.cn Zheng Jianyong 1，Li Weimin 2，Shi Jinfei 1 1. Department of Mechanical and Engineering，Southeast University，Nanjing （211189） 2. Department of Mechanical，Hebei University of Technology，Tianjin (300130) Abstract One kind of three degree of freedom translational parallel mechanism’s configuration analysis was proposed in the article, which had been obtained from the movement pair-analysis. The mechanism has three orthogonal distributional branch-chains, and all movement pairs are rotational joints, which moving platform has X, Y, Z three translational direction of decoupling. It also had carried on the kinematics research according to the parallel mechanism characteristics. The direct kinematics and inverse kinematics were solved and the input/output speed, the acceleration analysis had been carried on in the paper, which confirmed its decoupling characteristics of the movement. This was the certain significant theory for the following study of its dynamics analysis, controlling strategy, mechanism design, path planning etc. Keywords：Three Degree Parallel Mechanism，Configuration，Kinematics，Decoupling 作者简介：郑建勇：1978年生，男，东南大学机械工程学院，在读博士研究生，机械电子工程专业，研究方向为机器人技术与应用，发表论文一篇，参与申请专利一项(200610013060.2)；史金飞：1964年生，男，东南大学机械工程学院长，教授，博士生导师；李为民：1964年生，男，河北工业大学机械学院，教授，博士生导师。 - 6 -

资料库

一种三自由度并联机构的构型与运动学分析.pdf

相关推荐

开发技术

热门标签

最新资料