《图卷积神经网络》中文综述论文.pdf

发布时间：2022-06-19 发布人：admin 分类：说明书资料大小：3.00M 资料格式：pdf 举报版权申诉

339df59e-46f8-432a-a8fd-37c1dede767f.pdf-第1页.png

第1页 / 共26页

339df59e-46f8-432a-a8fd-37c1dede767f.pdf-第2页.png

第2页 / 共26页

339df59e-46f8-432a-a8fd-37c1dede767f.pdf-第3页.png

第3页 / 共26页

339df59e-46f8-432a-a8fd-37c1dede767f.pdf-第4页.png

第4页 / 共26页

339df59e-46f8-432a-a8fd-37c1dede767f.pdf-第5页.png

第5页 / 共26页

339df59e-46f8-432a-a8fd-37c1dede767f.pdf-第6页.png

第6页 / 共26页

339df59e-46f8-432a-a8fd-37c1dede767f.pdf-第7页.png

第7页 / 共26页

339df59e-46f8-432a-a8fd-37c1dede767f.pdf-第8页.png

第8页 / 共26页

文本预览

第４３卷　第５期２０２０年５月计　　算　　机　　学　　报ＣＨＩＮＥＳＥＪＯＵＲＮＡＬＯＦＣＯＭＰＵＴＥＲＳＶｏｌ．４３Ｎｏ．５Ｍａｙ２０２０　图卷积神经网络综述徐冰冰１），２），３）　岑科廷１），２），３）　黄俊杰１），２），３）　沈华伟１），２）　程学旗１），２）１）（中国科学院网络数据科学与技术重点实验室　北京　１００１９０）２）（中国科学院计算技术研究所　北京　１００１９０）３）（中国科学院大学　北京　１０００４９）摘　要　过去几年，卷积神经网络因其强大的建模能力引起广泛关注，在自然语言处理、图像识别等领域成功应用．然而，传统的卷积神经网络只能处理欧氏空间数据，而现实生活中的许多场景，如交通网络、社交网络、引用网络等，都是以图数据的形式存在．将卷积神经网络迁移到图数据分析处理中的核心在于图卷积算子的构建和图池化算子的构建．本文对图卷积神经网络进行综述，首先介绍了图卷积神经网络的背景并梳理了两类经典方法——— 谱方法和空间方法．针对图数据上平移不变性的缺失给图卷积算子的定义带来的困难，谱方法借助卷积定理在谱域定义图卷积，而空间方法通过在节点域定义节点相关性来实现图卷积．进而，本文介绍了图卷积神经网络的最新进展，这其中包括如何利用图卷积神经网络建模图上的复杂信息，如异质连接、高阶连接等，以及如何在大规模图上实现图卷积神经网络；此外，本文介绍了图卷积神经网络的相关应用，包括推荐系统领域、交通预测领域等；最后本文对图卷积神经网络的发展趋势进行了总结和展望．关键词　图卷积神经网络；卷积；池化；非欧空间中图法分类号ＴＰ１８　　　犇犗犐号１０．１１８９７／ＳＰ．Ｊ．１０１６．２０２０．００７５５犃犛狌狉狏犲狔狅狀犌狉犪狆犺犆狅狀狏狅犾狌狋犻狅狀犪犾犖犲狌狉犪犾犖犲狋狑狅狉犽ＸＵＢｉｎｇＢｉｎｇ１），２），３）ＣＥＮＫｅＴｉｎｇ１），２），３）ＨＵＡＮＧＪｕｎＪｉｅ１），２），３）ＳＨＥＮＨｕａＷｅｉ１），２）ＣＨＥＮＧＸｕｅＱｉ１），２）１）（犓犲狔犔犪犫狅狉犪狋狅狉狔狅犳犖犲狋狑狅狉犽犇犪狋犪犛犮犻犲狀犮犲犪狀犱犜犲犮犺狀狅犾狅犵狔，犆犺犻狀犲狊犲犃犮犪犱犲犿狔狅犳犛犮犻犲狀犮犲狊，犅犲犻犼犻狀犵　１００１９０）２）（犐狀狊狋犻狋狌狋犲狅犳犆狅犿狆狌狋犻狀犵犜犲犮犺狀狅犾狅犵狔，犆犺犻狀犲狊犲犃犮犪犱犲犿狔狅犳犛犮犻犲狀犮犲狊，犅犲犻犼犻狀犵　１００１９０）３）（犝狀犻狏犲狉狊犻狋狔狅犳犆犺犻狀犲狊犲犃犮犪犱犲犿狔狅犳犛犮犻犲狀犮犲狊，犅犲犻犼犻狀犵　１０００４９）犃犫狊狋狉犪犮狋　Ｉｎｔｈｅｐａｓｔｆｅｗｙｅａｒｓ，ｃｏｎｖｏｌｕｔｉｏｎａｌｎｅｕｒａｌｎｅｔｗｏｒｋｈａｓａｔｔｒａｃｔｅｄｗｉｄｅｓｐｒｅａｄａｔｔｅｎｔｉｏｎｄｕｅｔｏｉｔｓｐｏｗｅｒｆｕｌｍｏｄｅｌｉｎｇｃａｐａｂｉｌｉｔｉｅｓ，ａｎｄｈａｓａｃｈｉｅｖｅｄｇｒｅａｔｉｍｐｒｏｖｅｍｅｎｔｉｎａｒｅａｓｓｕｃｈａｓｎａｔｕｒａｌｌａｎｇｕａｇｅｐｒｏｃｅｓｓｉｎｇａｎｄｃｏｍｐｕｔｅｒｖｉｓｉｏｎ．ＴｒａｄｉｔｉｏｎａｌｃｏｎｖｏｌｕｔｉｏｎａｌｎｅｕｒａｌｎｅｔｗｏｒｋｃａｎｏｎｌｙｐｒｏｃｅｓｓＥｕｃｌｉｄｅａｎｄａｔａ．Ｈｏｗｅｖｅｒ，ｍａｎｙｒｅａｌｌｉｆｅｓｃｅｎａｒｉｏｓ，ｓｕｃｈａｓｔｒａｎｓｐｏｒｔａｔｉｏｎｎｅｔｗｏｒｋｓ，ｓｏｃｉａｌｎｅｔｗｏｒｋｓａｎｄｃｉｔａｔｉｏｎｎｅｔｗｏｒｋｓ，ａｒｅｌｏｃａｔｅｄｉｎｔｈｅｆｏｒｍｏｆｇｒａｐｈｄａｔａ．Ｔｈｅｍｅｔｈｏｄｕｓｅｄｔｏｐｒｏｃｅｓｓｇｒａｐｈｄａｔａｐｒｅｖｉｏｕｓｌｙｉｓｎｅｔｗｏｒｋｅｍｂｅｄｄｉｎｇ．Ｓｐｅｃｉｆｉｃａｌｌｙ，ｔｈｅｒｅｓｅａｒｃｈｅｒｓｍｏｄｅｌｔｈｅｇｒａｐｈｂａｓｅｄｍｉｓｓｉｏｎｉｎｔｏａｔｗｏｓｔａｇｅｍｏｄｅｌ．Ｉｎｔｈｅｆｉｒｓｔｓｔａｇｅ，ａｆｉｘｅｄｌｅｎｇｔｈｒｅｐｒｅｓｅｎｔａｔｉｏｎｉｓｌｅａｒｎｅｄｆｏｒｅａｃｈｎｏｄｅｖｉａｃａｐｔｕｒｉｎｇｔｈｅｐｒｏｘｉｍｉｔｙｏｖｅｒｎｏｄｅｓ，ｔｈｉｓｒｅｐｒｅｓｅｎｔａｔｉｏｎｉｓｆｅｄｉｎｔｏｔｈｅｓｅｃｏｎｄｓｔａｇｅｔｏｓｏｌｖｅｄｏｗｎｓｔｒｅａｍｔａｓｋｓ，ｅ．ｇ．，ｌｉｎｋｐｒｅｄｉｃｔｉｏｎ，ｎｏｄｅｃｌａｓｓｉｆｉｃａｔｉｏｎａｎｄｇｒａｐｈｃｌａｓｓｉｆｉｃａｔｉｏｎ．Ｉｎｒｅｃｅｎｔｙｅａｒｓ，ｔｈｅｐｏｗｅｒｆｕｌｍｏｄｅｌｉｎｇｃａｐａｂｉｌｉｔｉｅｓｏｆｃｏｎｖｏｌｕｔｉｏｎａｌｎｅｕｒａｌｎｅｔｗｏｒｋ收稿日期：２０１９０５０６；在线出版日期：２０１９１１０４．本课题得到国家自然科学基金项目（６１４２５０１６，９１７４６３０１）、北京智源人工智能研究院和王宽诚教育基金会资助．徐冰冰，博士研究生，中国计算机学会（ＣＣＦ）学生会员，主要研究方向为图神经网络、图上半监督学习．Ｅ ｍａｉｌ：ｘｕｂｉｎｇｂｉｎｇ＠ｉｃｔ．ａｃ．ｃｎ．岑科廷（共同第一作者），博士研究生，中国计算机学会（ＣＣＦ）学生会员，主要研究方向为网络表示学习、图神经网络．Ｅｍａｉｌ：ｃｅｎｋｅｔｉｎｇ＠ｉｃｔ．ａｃ．ｃｎ．黄俊杰（共同第一作者），硕士研究生，主要研究方向为社会媒体计算、图神经网络．Ｅｍａｉｌ：ｈｕａｎｇｊｕｎｊｉｅ１７ｓ＠ｉｃｔ．ａｃ．ｃｎ．沈华伟（通信作者），博士，研究员，中国计算机学会（ＣＣＦ）高级会员，主要研究领域为社交网络分析和社会媒体计算．Ｅｍａｉｌ：ｓｈｅｎｈｕａｗｅｉ＠ｉｃｔ．ａｃ．ｃｎ．程学旗，博士，研究员，中国计算机学会（ＣＣＦ）会士，主要研究领域为大数据分析与挖掘、网络科学、网络信息安全以及互联网搜索与数据挖掘．《计算机学报》

６５７计　　算　　机　　学　　报２０２０年ａｎｄｔｈｅｕｂｉｑｕｉｔｙｏｆｇｒａｐｈｄａｔａｈａｖｅｉｎｓｐｉｒｅｄｒｅｓｅａｒｃｈｅｒｓｔｏｔｒａｎｓｆｅｒｃｏｎｖｏｌｕｔｉｏｎａｌｎｅｕｒａｌｎｅｔｗｏｒｋｔｏｇｒａｐｈｓ，ｗｈｉｃｈｃａｎｓｏｌｖｅｔｈｅｇｒａｐｈｂａｓｅｄｔａｓｋｖｉａａｎｅｎｄｔｏｅｎｄｍａｎｎｅｒ．Ｔｈｅｃｏｒｅｏｆｇｒａｐｈｃｏｎｖｏｌｕｔｉｏｎａｌｎｅｕｒａｌｎｅｔｗｏｒｋｉｓｔｈｅｃｏｎｓｔｒｕｃｔｉｏｎｏｆｇｒａｐｈｃｏｎｖｏｌｕｔｉｏｎｏｐｅｒａｔｏｒａｎｄｐｏｏｌｉｎｇｏｐｅｒａｔｏｒ．Ｉｎｔｈｉｓｐａｐｅｒ，ｗｅｒｅｖｉｅｗｔｈｅｇｒａｐｈｃｏｎｖｏｌｕｔｉｏｎａｌｎｅｕｒａｌｎｅｔｗｏｒｋ．Ｆｉｒｓｔｌｙ，ｔｈｅｂａｃｋｇｒｏｕｎｄｏｆｇｒａｐｈｃｏｎｖｏｌｕｔｉｏｎａｌｎｅｕｒａｌｎｅｔｗｏｒｋａｎｄｉｔｓｃｌａｓｓｉｃａｌｍｅｔｈｏｄｓａｒｅｉｎｔｒｏｄｕｃｅｄ，ｉｎｃｌｕｄｉｎｇｓｐｅｃｔｒａｌｍｅｔｈｏｄｓａｎｄｓｐａｔｉａｌｍｅｔｈｏｄｓ．Ｔｈｅｌａｃｋｏｆｔｒａｎｓｌａｔｉｏｎｉｎｖａｒｉａｎｃｅｏｎｔｈｅｇｒａｐｈｄａｔａｍａｋｅｓｉｔｄｉｆｆｉｃｕｌｔｔｏｄｅｆｉｎｅｔｈｅｇｒａｐｈｃｏｎｖｏｌｕｔｉｏｎｏｐｅｒａｔｏｒ．Ｔｈｅｓｐｅｃｔｒａｌｍｅｔｈｏｄｓｄｅｆｉｎｅｔｈｅｃｏｎｖｏｌｕｔｉｏｎｉｎｔｈｅｓｐｅｃｔｒａｌｄｏｍａｉｎｖｉａｔｈｅｃｏｎｖｏｌｕｔｉｏｎｔｈｅｏｒｅｍ，ｗｈｉｌｅｔｈｅｓｐａｔｉａｌｍｅｔｈｏｄｓｉｍｐｌｅｍｅｎｔｔｈｅｇｒａｐｈｃｏｎｖｏｌｕｔｉｏｎｂｙｄｅｆｉｎｉｎｇｔｈｅｎｏｄｅｃｏｒｒｅｌａｔｉｏｎｉｎｔｈｅｎｏｄｅｄｏｍａｉｎ．Ｔｈｅｎ，ｔｈｅｌａｔｅｓｔｄｅｖｅｌｏｐｍｅｎｔｓａｒｅｉｎｔｒｏｄｕｃｅｄ．Ｒｅｃｅｎｔｒｅｓｅａｒｃｈｅｒｓｆｏｃｕｓｏｎｈｏｗｔｏｍｏｄｅｌｔｈｅｃｏｍｐｌｉｃａｔｅｄｉｎｆｏｒｍａｔｉｏｎｏｎｇｒａｐｈｖｉａｇｒａｐｈｃｏｎｖｏｌｕｔｉｏｎｎｅｕｒａｌｎｅｔｗｏｒｋ，ｅ．ｇ．，ｈｅｔｅｒｏｇｅｎｅｏｕｓｃｏｎｎｅｃｔｉｏｎａｎｄｈｉｇｈｏｒｄｅｒｃｏｎｎｅｃｔｉｏｎ．Ｉｎａｄｄｉｔｉｏｎ，ｈｏｗｔｏｃｏｎｓｔｒｕｃｔｇｒａｐｈｃｏｎｖｏｌｕｔｉｏｎｎｅｕｒａｌｎｅｔｗｏｒｋｏｎｌａｒｇｅｓｃａｌｅｎｅｔｗｏｒｋａｌｓｏａｔｔｒａｃｔｓｍｕｃｈａｔｔｅｎｔｉｏｎ．Ｍｏｒｅｏｖｅｒ，ｗｅｃｏｎｃｌｕｄｅｔｈｅｇｒａｐｈｃｏｎｖｏｌｕｔｉｏｎｎｅｕｒａｌｎｅｔｗｏｒｋｉｎｍａｎｙａｐｐｌｉｃａｔｉｏｎｓ，ｉｎｃｌｕｄｉｎｇｔｒａｆｆｉｃｐｒｅｄｉｃｔｉｏｎａｎｄｒｅｃｏｍｍｅｎｄｅｒｓｙｓｔｅｍ．Ｆｉｎａｌｌｙ，ｔｈｅｄｅｖｅｌｏｐｉｎｇｔｒｅｎｄｏｆｇｒａｐｈｃｏｎｖｏｌｕｔｉｏｎａｌｎｅｕｒａｌｎｅｔｗｏｒｋｉｓｓｕｍｍａｒｉｚｅｄａｎｄｆｏｒｅｃａｓｔｅｄ．犓犲狔狑狅狉犱狊　ｇｒａｐｈｃｏｎｖｏｌｕｔｉｏｎａｌｎｅｕｒａｌｎｅｔｗｏｒｋ；ｃｏｎｖｏｌｕｔｉｏｎ；ｐｏｏｌｉｎｇ；ｎｏｎＥｕｃｌｉｄｅａｎｓｐａｃｅ１　引　言过去几年，卷积神经网络［１２］快速发展，并借由其强大的建模能力引起广泛关注．相比传统方法，卷积神经网络的引入给图像处理［３］和自然语言处理等领域带来了很大的提升，如机器翻译［４］、图像识别［５］和语音识别［６］等．但是，传统的卷积神经网络只能处理欧氏空间数据（如图像、文本和语音），这些领域的数据具有平移不变性．平移不变性使得我们可以在输入数据空间定义全局共享的卷积核，从而定义卷积神经网络．以图像数据为例，一张图片可以表示为欧氏空间中一组规则散布的像素点，平移不变性则表示以任意像素点为中心，可以获取相同尺寸的局部结构．基于此，卷积神经网络通过学习在每个像素点共享的卷积核来建模局部连接，进而为图片学习到意义丰富的隐层表示．尽管传统的卷积神经网络在文本和图像领域带来提升，但是它仅能处理欧氏空间数据．而同时，一种非欧空间数据：图数据，因其普遍存在性逐渐受到关注．图数据可以自然的表达实际生活中的数据结构，如交通网络、万维网和社交网络等．不同于图像和文本数据，图数据中每个节点的局部结构各异，这使得平移不变性不再满足［７］．平移不变性的缺失给在图数据上定义卷积神经网络提出了挑战．近年来，由于图数据的普遍存在性，研究人员开始关注如何在图上构造深度学习模型．借助于卷积神经网络对局部结构的建模能力及图上普遍存在的节点依赖关系，图卷积神经网络成为其中最活跃最重要的一支．近期陆续涌现出一些文章探索图上深度学习并对其进行综述［８９］，但是针对其中最重要的分支，图卷积神经网络，其建模方法和应用方面的深入探讨和总结仍为空白．对此，我们在本篇文章中深入整理总结了图卷积神经网络的发展历程及其未来趋势．图卷积神经网络的构建所面临的挑战主要来源于以下几个方面：（１）图数据是非欧空间数据图数据作为非欧空间数据，不满足平移不变性，即每个节点具有各异的局部结构．而传统卷积神经网络中的基本算子：卷积和池化，依赖于数据的平移不变性．此时如何在图数据上定义卷积和池化算子成为一个有挑战的工作．（２）图数据具有多样的特性实际生活中的多种应用都可以用图数据自然的表示，这使得图数据具有多样的特性，如社交网络中用户的有向连接，引文网络中作者和引文的异质连接，政治关系网络中的正负倾向带符号连接等．多样的图特性给图卷积神经网络的构建带来更多信息，但是多种特性的建模也要求图卷积神经网络的设计更加复杂精细，给图卷积神经网络带来新的挑战．（３）图数据的规模很大《计算机学报》

５期徐冰冰等：图卷积神经网络综述７５７在大数据时代，实际应用中的图可能规模极大，含有百万甚至千万级别的节点，如推荐系统中的用户商品网络，社交网络中的用户网络．如何在时间和空间可接受范围内在大规模图上构建图卷积神经网络也是非常大的挑战．１１　现有方法及分类图数据建模的历史由来已久．起初，研究人员关注统计分析的方法，这个时期没有机器学习模型的参与，如网页排序的常用算法ＰａｇｅＲａｎｋ［１０］、ＨＩＴＳ［１１］等．此外，研究人员也借用图谱理论的知识，如用拉普拉斯矩阵的特征值和特征向量做社区分析或者人群聚类［１２］等．随着深度学习的崛起，研究人员开始考虑把深度学习的模型引入到图数据中，代表性的研究工作是网络嵌入（ＮｅｔｗｏｒｋＥｍｂｅｄｄｉｎｇ）［１３］，即通过约束节点的邻近性为每个节点学习固定长度的表达，如ＤｅｅｐＷａｌｋ［１４］、ＬＩＮＥ［１５］、ｎｏｄｅ２ｖｅｃ［１６］等．这一时期，在解决具体的应用问题时，研究人员通常将其建模为两阶段问题，以节点分类为例，第一阶段为每个节点学习统一长度的表达，第二阶段将节点表达作为输入，训练分类模型．近年来，研究人员对图数据建模的关注逐渐转移到如何将深度学习的模型迁移到图数据上，进行端到端的建模，而图卷积神经网络则是其中最活跃的一支．在建模图卷积神经网络时，研究人员关注如何在图上构建卷积算子．Ｂｒｕｎａ等人［１７］在２０１３年提出第一个图卷积神经网络，他们基于图谱理论从卷积定理出发，在谱空间定义图卷积．这一支后来发展为图卷积领域的谱方法．最初的谱方法具有时空复杂度较高的弊端，ＣｈｅｂＮｅｔ［１８］和ＧＣＮ［１９］对谱方法中的卷积核进行参数化，大大降低了时空复杂度．这两个方法虽然被归为谱方法，但已经开始从空间角度定义节点的权重矩阵．在这两个方法的启发下，空间方法应用而生，开始考虑在节点域用注意力机制、序列化模型等建模节点间的权重．这一时期的图卷积神经网络在构建卷积算子过程中没有过多的考虑图特性，随着卷积算子的逐渐完善，人们开始考虑多样的图特性，如开始关注如何建模图上的高阶信息，并分别针对边上带特征的图、异质图等进行精细设计．此外，如何训练更高效的图卷积神经网络也受到广泛关注．研究人员开始试图训练更深层的图卷积神经网络，以增强模型的泛化能力．同时，模型到大规模图的可扩展性以及训练的速度也是图卷积神经网络中非常重点的研究方向．表１展示了图卷积神经网络的主要方法．表１　图卷积神经网络的主要方法相关论文方法基于卷积定理的图卷积神经网络ＳｐｅｃｔｒａｌＣＮＮ［１７］，ＣｈｅｂｙＮｅｔ［１８］，ＧＣＮ［１９］，Ｈｅｎａｆｆ等人［２０］，ＧＷＮＮ［２１］，ＧｒａｐｈＨｅａｔ［２２］，基于聚合函数的图卷积神经网络ＭｏＮｅｔ［２５］，ＭＰＮＮｓ［２６］，ＧＮＮｓ［２７］，ＧＡＴ［２８］，ＧｒａｐｈＳＡＧＥ［２９］，ＤＣＮＮ［３０］，ＣｏｎｆＧＣＮ［３１］，建模边上信息的图卷积神经网络ＲＧＣＮｓ［３３］，ＲＧＡＴ［３４］，ＳＧＣＮ［３５］，ＤＰＧＣＮＮ［３６］，ＥＧＡＴ［３７］，ＥＣＣ［３８］建模高阶信息的图卷积神经网络ＨＡＧＣＮ［３９］，ＭｏｔｉｆＣＮＮ［４０］，ＨＡＮ［４１］，ＭＣＮ［４２］，ＭｏｔｉｆＮｅｔ［４３］深层图卷积神经网络大规模图卷积神经网络ＧｒａｐｈＳＡＧＥ［２９］，ＰｉｎＳａｇｅ［４６］，ＣｏｎｔｒｏｌＶａｒｉａｔｅＢａｓｅｄＡｌｇｏｒｉｔｈｍ（ＣＶ）［４７］，ＦａｓｔＧＣＮ［４８］，Ａｄａｐｔ［４９］ＪｕｍｐｉｎｇＫｎｏｗｌｅｄｇｅＮｅｔｗｏｒｋ［４４］，ＣｏＴｒａｉｎ［４５］ＰＰＮＰ［２３］，ＳＰＣ［２４］ＨＧＮＮ［３２］关注领域关注卷积算子构建关注图上复杂信息建模关注训练过程优化　　池化算子作为卷积神经网络的主要组成部分，作用是扩大感受野，降低参数．近期，也有研究开始关注图上池化算子的构建．图上池化算子主要用于图分类问题，目的是学习到图的层级结构．１２　任务图数据建模所针对的应用场景非常广泛，这也使得图数据建模所处理的任务多样．我们将下游任务分为节点级别的任务和图级别的任务，节点级别的任务包括节点分类，链接预测等，如引文网络中的文章分类，推荐系统中用户对商品的偏好推断．图级别的任务包括图生成，图分类等，如药物网络生成，蛋白质网络中的蛋白质分类．１３　章节组织本文第２节给定全文的符号定义；第３节回顾初期图卷积网络中卷积算子和池化算子的定义，其中卷积算子定义部分又包括了空间方法和谱方法；第４节主要关注图卷积神经网络的一些新进展，包括图特性建模和训练优化两个部分；第５节我们详细介绍了图卷积神经网络在现有各种典型应用下图的构造及卷积的定义；在第６节和第７节中，我们给出图卷积神经网络的未来发展展望，并总结全文．２　符号定义在这一节中，我们给出文中常见符号的定义．《计算机学报》

计　　算　　机　　学　　报２０２０年方法．现有的图卷积神经网络分为谱方法和空间方法两类，谱方法利用图上卷积定理从谱域定义图卷积，而空间方法从节点域出发，通过定义聚合函数来聚合每个中心节点和其邻近节点．３．１．１　图卷积神经网络谱方法图上平移不变性的缺失，给在节点域定义卷积神经网络带来困难．谱方法利用卷积定理从谱域定义图卷积．我们首先给出卷积定理的背景知识．８５７表２展示了每种符号的代表含义．表示含义表２　符号定义图节点集合连边集合节点个数单位阵邻接矩阵度矩阵（对角阵）拉普拉斯矩阵特征向量矩阵特征值矩阵（对角阵）第犻个特征向量节点特征矩阵第犻个节点的特征信号符号犌犞犈狀犐狀∈犚狀×狀犃∈犚狀×狀犇∈犚狀×狀犔∈犚狀×狀犝∈犚狀×狀 Λ∈犚狀×狀狌犻∈犚狀犡∈犚狀×犇犡犻∈犚犇犳∈犚狀我们用犌＝｛犞，犈，犃｝表示无向图，其中犞表示节点集合，｜犞｜＝狀表示图上共有狀个节点，犈表示边集合，犃表示邻接矩阵，定义节点之间的相互连接，且在无向图中犃犻，犼＝犃犼，犻．犔＝犇－犃表示图上的拉普拉斯矩阵，其中犇是一个对角阵，犇犻，犻表示第犻个节点的度且犇犻，犻＝∑犼犃犻，犼．归一化后的拉普拉斯矩２，其中犐狀∈犚狀×狀是单位阵定义为犔＝犐狀－犇－１２犃犇－１阵．因为犔是一个实对称矩阵，对犔做特征分解得到犔＝犝Λ犝Ｔ．其中犝＝｛狌犻｝狀犻＝１表示狀个相互正交的特征向量．Λ＝ｄｉａｇ（｛λ犻｝狀犻＝１）是一个对角阵，λ犻表示狌犻对应的特征值．我们用犡表示图犌上的节点特征，其中犡∈ 犚狀×犇，犡犻∈犚犇是第犻节点的特征，犡犻犼表示矩阵犡的第犻行第犼列，即第犻节点的第犼个特征．犳，狓，狔∈ 犚狀表示图上的信号，其中犳犻表示节点犻在信号犳上的取值．３　图卷积神经网络图卷积神经网络主要包括卷积算子和池化算子的构建，其中卷积算子的目的是刻画节点的局部结构，而池化算子的目的是学到网络的层级化表示，降低参数．在解决节点级别的任务时，研究人员更关注如何给每个节点学到更好的表达，此时池化算子并不必要，因此前期大量的工作仅关注图上卷积算子的构建，而池化算子通常用在图级别的任务上．在这一章节中，我们将详细介绍图上卷积算子和池化算子的构建．３１　图卷积算子的构建本节介绍关注卷积算子构建的图卷积神经网络（１）图信号处理卷积定理：信号卷积的傅立叶变换等价于信号傅立叶变换的乘积［７］：犉（犳×犵）＝犉（犳）·犉（犵）（１）其中，犳，犵表示两个原始信号，犉（犳）表示犳的傅立叶变换，·表示乘积算子，表示卷积算子．对式（１）两端做傅立叶逆变换，可以得到犳犵＝犉－１（犉（犳）·犉（犵））（２）其中，犉－１（犳）表示信号犳的傅立叶逆变换．利用卷积定理，我们可以对谱空间的信号做乘法，再利用傅里叶逆变换将信号转换到原空间来实现图卷积，从而避免了因图数据不满足平移不变性而造成的卷积定义困难问题．图上傅立叶变换依赖于图上的拉普拉斯矩阵，在下文中，我们将给出图上傅立叶变换的定义．图上傅立叶变换的定义依赖于拉普拉斯矩阵的特征向量．以特征向量作为谱空间下的一组基底，图上信号狓的傅立叶变换为（３）其中，狓指信号在节点域的原始表示．狓＾指信号狓变换到谱域后的表示，犝Ｔ表示特征向量矩阵的转置，用于做傅立叶变换．信号狓的傅立叶逆变换为（４）利用图上傅立叶变换和逆变换，我们可以基于卷积定理实现图卷积算子狓犌狔＝犝（（犝Ｔ狓）⊙（犝Ｔ狔））（５）其中，犌表示图卷积算子，狓，狔表示图上节点域的信号，⊙指哈达玛乘法，表示两个向量的对应元素相乘．我们用一个对角阵犵θ代替向量犝Ｔ狔，那么哈达玛乘法可以转化成矩阵乘法．将卷积核犵θ作用在信号上，图卷积可以表示成如下形式（６）犝犵θ犝Ｔ狓　　卷积定理提供了通过傅立叶变换在图上定义卷积的方式．基于此卷积算子的定义，国内外陆续涌现出一些图卷积神经网络．狓＾＝犝Ｔ狓狓＝犝狓＾（２）基于卷积定理的图卷积神经网络谱卷积神经网络（ＳｐｅｃｔｒａｌＣＮＮ）［１７］是最早提《计算机学报》

徐冰冰等：图卷积神经网络综述９５７效；（４）热核函数中的超参数狊用以表示热量扩散的范围，通过调节超参数狊可以灵活的适应于不同任务场景．图１指在不同狊下黄色节点对应的小波变换基底．图１（ａ）表示在狊较小时，以黄色节点为中心进行的热量扩散，图１（ｂ）表示当狊增大时，热量扩散范围也变大；此外，图１（ａ）也反应了小波基底的局部性和稀疏性．犻＝１（犼＝犺犝∑狆犉犿犡犿＋１犻，犼犝⊥犡犿５期出在图上构建卷积神经网络的方法，该方法利用卷积定理在每一层定义图卷积算子，在损失函数指导下通过梯度反向回传学习卷积核，并堆叠多层组成神经网络．谱卷积神经网络第犿层的结构如下）犻，犼＝１，…，狇（７）其中，狆，狇分别是输入特征和输出特征的维度，犡犿犻∈ 犚狀表示图上节点在第犿层的第犻个输入特征，犉犿犻，犼表示谱空间下卷积核，犺表示非线性激活函数．在谱卷积神经网络中，这样一层结构将特征从狆维转化到狇维，且基于卷积定理通过学习卷积核实现了图卷积．谱卷积神经网络将卷积核作用在谱空间的输入信号上，并利用卷积定理实现图卷积，以完成节点之间的信息聚合，然后将非线性激活函数作用在聚合结果上，并堆叠多层形成神经网络．该模型不满足局部性，使得谱卷积神经网络的局部性没有保证，即产生信息聚合的节点并不一定是邻近节点．建模图卷积神经网络的初衷是为了利用图结构刻画邻近节点的信息聚合，而上文介绍的谱卷积神经网络并不满足局部性，Ｈｅｎａｆｆ等人［２０］提出用带有平滑性约束的插值卷积核，这种方法降低参数个数且实现了图卷积神经网络的局部化．最近，小波神经网络（ＧＷＮＮ）［２１］提出用小波变换代替傅立叶变换实现卷积定理．小波神经网络指出，与傅立叶变换相似，小波变换也定义了一种将信号从节点域变换到谱域的方法［５０］．这里用Ψ狊＝｛ψ狊１，ψ狊２，…，ψ狊狀｝表示小波变换的基底，其中ψ狊犻表示从第犻个节点出发的能量扩散，刻画了第犻个节点的局部结构．小波基底的定义依赖于拉普拉斯矩阵的特征向量，即Ψ狊＝犝犌狊犝Ｔ，其中犌狊＝ｄｉａｇ（｛犵狊（λ犻）｝狀犻＝１），对角线元素由犵函数作用到特征值上得到．不同的犵函数赋予小波基底不同的性质，在小波神经网络中，作者使用热核函数，即犵狊（λ犻）＝犲狊λ犻．以Ψ狊为谱空间的基底，图上小波逆变换的变换矩阵为Ψ－１狊＝犝犌－狊犝Ｔ，其中犌－狊表示将上述犵函数替换为犵－狊（λ犻）＝犲－狊λ犻．和傅立叶变换相比，小波变换的基底具有几个很好的性质：（１）小波变换的基底可以通过切比雪夫多项式近似得到，避免拉普拉斯矩阵特征分解的高昂代价；（２）小波变换的基底具有局部性；（３）小波基底的局部性使得小波变换矩阵非常稀疏，这大狊狓的计算复杂度，使计算过程更加高大降低了Ψ－１网络的第犿层结构定义如下：狊犡犿图１　不同狊下的小波变换基底［２１］（（ａ）当狊较小时，以黄色节点为中心的热量扩散范围较小；（ｂ）当狊增大时，热量扩散范围增大）利用图上小波变换代替傅立叶变换，小波神经）犻，犼＝１，…，狇（８）　　与谱卷积神经网络相比，小波神经网络用小波变换代替傅立叶变换，即用Ψ和Ψ－１狊替代了犝和犝⊥．在这样一组小波基底下，图卷积神经网络满足了局部性，且由于小波基底的可加速计算以及稀疏性，图卷积神经网络的计算复杂度也大大降低．犼＝犺Ψ狊∑狆犉犿犡犿＋１犻，犼Ψ－１（犻＝１除小波神经网络外，还有一些工作致力于实现图卷积神经网络的局部性和加速计算，但不同于小波神经网络更换基底的方式，这些工作通过参数化卷积核实现局部性，同时降低参数复杂度和计算复杂度．下文我们将给出这类工作的具体介绍．在式（６）中，犵θ是需要学的卷积核，在谱卷积神经网络中，犵θ是对角阵的形式，且有狀个需要学的参数．切比雪夫网络（ＣｈｅｂｙＮｅｔ）［１８］对卷积核犵θ进行参数化犻＝０犵θ＝∑犓－１ θ犽犜犽（＾Λ）其中，θ犽是需要学的系数，＾Λ＝２Λ 项式是通过递归得到，递归表达式为（９） λｍａｘ－犐狀．切比雪夫多犜犽（狓）＝２狓犜犽－１（狓）－犜犽－２（狓）（１０）其中，犜０（狓）＝１，犜１（狓）＝狓．令＾犔＝２犔 λｍａｘ－犐狀，切比雪夫网络第犿层的结构定义如下：《计算机学报》

犽＝０犽＝０犻＝１ θ犽犜犽（＾Λ（ θ犽犜犽（＾犔）犡犿０６７（犻＝１∑犓－１犼＝犺犝∑狆犡犿＋１（犻＝１∑犓－１＝犺∑狆）犻　　　　））犝⊥犡犿）犻，犼＝１，…，狇（１１）切比雪夫网络利用特征值矩阵的多项式参数化卷积核，实现谱卷积神经网络，且巧妙的利用犔＝犝Λ犝Ｔ引入拉普拉斯矩阵，从而避免了拉普拉斯矩阵的特征分解，同时参数复杂度从犗（狀×狆×狇）下降到犗（犓× 狆×狇）．此外，在拉普拉斯矩阵中，当且仅当节点犻，犼满足犓跳可达时，犔犓犻，犼≠０，这一性质使得当犓较小时，切比雪夫网络具有局部性．（θ０－θ１（犔－犐狀））犡犿为了使图卷积神经网络在图上半监督学习领域发挥作用，Ｋｉｐｆ等人［１９］对切比雪夫网络简化并提出一阶图卷积神经网络，Ｋｉｐｆ等人［１９］令犓＝２且λｍａｘ＝２，则式（１１）可以写成）犻，犼＝１，…，狇犼＝犺∑狆犡犿＋１（１２）　　在图上半监督学习场景下，带标签的数据非常少，为了避免模型过拟合，Ｋｉｐｆ等人约束θ＝θ０＝－θ１来降低模型参数，并对权重矩阵做归一化处理，最终得到如下的一阶图卷积神经网络）犻，犼＝１，…，狇（１３）犼＝犺∑狆 θ＾犇－１２＾犃＾犇－１２犡犿犡犿＋１其中，＾犃＝犃＋犐狀，且＾犇犻犻＝∑犼＾犃犻，犼．图热核网络（ＧｒａｐｈＨｅａｔ）［２２］从滤波器的角度对以上谱方法进行分析，指出谱卷积神经网络是非参滤波器，而切比雪夫网络和一阶图卷积神经网络都是高通滤波器，但这与图半监督学习的任务中的平滑性先验不一致，基于此，图热核网络利用热核函数参数化卷积核，进而实现低通滤波器．图热核网络的思想如图２所示．（（犻＝１图２　图热核网络与原有谱方法对比［２２］基于个性化ＰａｇｅＲａｎｋ的图卷积神经网络（ＰＰＮＰ）［２３］和简明一阶图卷积神经网络（ＳＧＣ）［２４］则是对一阶图卷积神经网络方法进行分析，并提出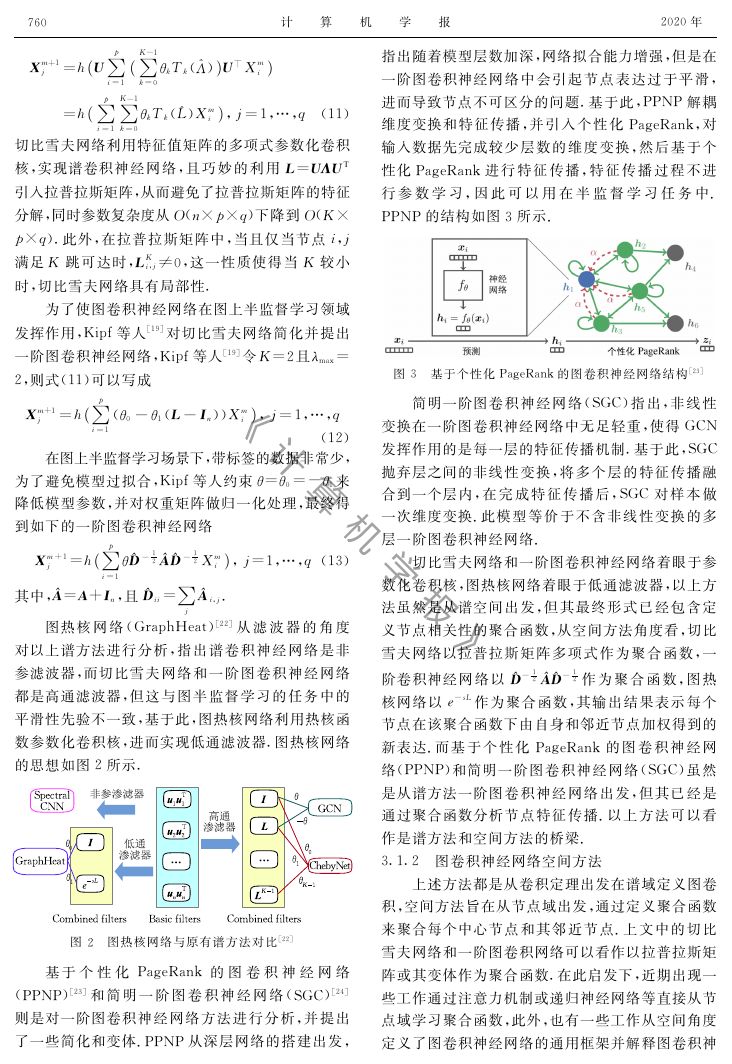了一些简化和变体．ＰＰＮＰ从深层网络的搭建出发，计　　算　　机　　学　　报２０２０年指出随着模型层数加深，网络拟合能力增强，但是在一阶图卷积神经网络中会引起节点表达过于平滑，进而导致节点不可区分的问题．基于此，ＰＰＮＰ解耦维度变换和特征传播，并引入个性化ＰａｇｅＲａｎｋ，对输入数据先完成较少层数的维度变换，然后基于个性化ＰａｇｅＲａｎｋ进行特征传播，特征传播过程不进行参数学习，因此可以用在半监督学习任务中．ＰＰＮＰ的结构如图３所示．图３　基于个性化ＰａｇｅＲａｎｋ的图卷积神经网络结构［２３］２＾犃＾犇－１简明一阶图卷积神经网络（ＳＧＣ）指出，非线性变换在一阶图卷积神经网络中无足轻重，使得ＧＣＮ发挥作用的是每一层的特征传播机制．基于此，ＳＧＣ抛弃层之间的非线性变换，将多个层的特征传播融合到一个层内，在完成特征传播后，ＳＧＣ对样本做一次维度变换．此模型等价于不含非线性变换的多层一阶图卷积神经网络．切比雪夫网络和一阶图卷积神经网络着眼于参数化卷积核，图热核网络着眼于低通滤波器，以上方法虽然是从谱空间出发，但其最终形式已经包含定义节点相关性的聚合函数，从空间方法角度看，切比雪夫网络以拉普拉斯矩阵多项式作为聚合函数，一阶卷积神经网络以＾犇－１２作为聚合函数，图热核网络以犲－狊犔作为聚合函数，其输出结果表示每个节点在该聚合函数下由自身和邻近节点加权得到的新表达．而基于个性化ＰａｇｅＲａｎｋ的图卷积神经网络（ＰＰＮＰ）和简明一阶图卷积神经网络（ＳＧＣ）虽然是从谱方法一阶图卷积神经网络出发，但其已经是通过聚合函数分析节点特征传播．以上方法可以看作是谱方法和空间方法的桥梁．３．１．２　图卷积神经网络空间方法上述方法都是从卷积定理出发在谱域定义图卷积，空间方法旨在从节点域出发，通过定义聚合函数来聚合每个中心节点和其邻近节点．上文中的切比雪夫网络和一阶图卷积网络可以看作以拉普拉斯矩阵或其变体作为聚合函数．在此启发下，近期出现一些工作通过注意力机制或递归神经网络等直接从节点域学习聚合函数，此外，也有一些工作从空间角度定义了图卷积神经网络的通用框架并解释图卷积神《计算机学报》

５期经网络的内部机制．徐冰冰等：图卷积神经网络综述（１）通用框架通用框架的定义指出图卷积网络的核心问题，同时给已有工作提供一个对比分析的平台．近期出现两篇文章旨在定义图卷积网络的通用框架，其中混合卷积网络（ＭｏＮｅｔ）［２５］着眼于图上平移不变性的缺失，通过定义映射函数将每个节点的局部结构映射为相同尺寸的向量，进而在映射后的结果上学习共享的卷积核；而消息传播网络（ＭＰＮＮｓ）［２６］立足于节点之间的信息传播聚合，通过定义聚合函数的通用形式提出框架．平移不变性的缺失给图卷积神经网络的定义带来困难．混合卷积网络在图上定义坐标系，并将节点之间的关系表示为新坐标系下的一个低维向量．同时，混合卷积网络定义一簇权重函数，权重函数作用在以一个节点为中心的所有邻近节点上，其输入为节点间的关系表示（一个低维向量），输出为一个标量值．通过这簇权重函数，混合卷积网络为每个节点获得相同尺寸的向量表示：犇犼（狓）犳＝∑狔∈犖（狓）狑犼（狌（狓，狔））犳（狔），犼＝１，…，犑（１４）其中，犖（狓）表示狓的邻近节点集合，犳（狔）表示节点狔在信号犳上的取值，狌（狓，狔）指坐标系狌下节点，关系的低维向量表示，狑犼表示第犼个权重函数，犑表示权重函数的个数．这步操作使得每个节点都得到一个犑维的表示，且这个表示融合了节点的局部结构信息．而混合卷积模型正是在这个犑维表示上定义共享卷积核，犵（犼）犇犼（狓）犳（１５）（犳犌犵）（狓）＝∑犑犼＝１犼＝１指卷积核．其中，｛犵（犼）｝犑不同于混合卷积网络，消息传播网络指出图卷积的核心在于定义节点之间的聚合函数，基于聚合函数，每个节点可以表示为周围节点和自身的信息叠加．因此，该模型通过定义通用的聚合函数提出图卷积网络的通用框架．消息传播网络分为两个步骤，首先将聚合函数作用在每个节点及其邻近节点上，得到节点的局部结构表达；然后，将更新函数作用在自身和局部结构表达上，得到当前节点的新表达，犿狋＋１狓＝∑狔∈犖（狓）犕狋（犺狋狓，犺狋狔，犲狓，狔），犺狋＋１狓＝犝狋（犺狋狓，犿狋＋１狓）（１６）其中，犺狋狓表示第狋步节点狓的隐层表示，犲狓，狔表示节点狓，狔的连边特征，犕狋表示第狋步的聚合函数，犿狋＋１狓表示节点狓通过聚合函数后得到的局部结构１６７表达，犝狋表示第狋步的更新函数．通过将神经网络的每一层设计成上述的聚合函数和更新函数，每个节点可以不断以自身和邻近节点为源信息更新自身，进而得到依赖于节点局部结构的新表达．在以上空间框架下，一些方法不再依赖于拉普拉斯矩阵，而是设计神经网络来学习聚合函数．这些方法学到的聚合函数可以自适应于任务和具体的图结构，有更大的灵活性．下文我们将给出这类方法的具体分析．（２）基于聚合函数的图卷积神经网络图神经网络（ＧＮＮｓ）［２７］是最早提出在图上搭建神经网络的模型．在图神经网络中，聚合函数被定义成循环递归函数的形式，每个节点以周围节点和连边作为来源信息更新自身的表达，狅狓＝犵狑（犺狓，犾狓）犺狓＝犳狑（犾狓，犾犮０［狓］，犾狀犲［狓］，犺狀犲［狓］）（１７）其中，犾狓，犾犮０［狓］，犾狀犲［狓］，犺狀犲［狓］分别表示节点狓的标签，与节点狓相连的边的标签，狓的邻居节点的标签，以及狓的邻居节点上一个时间步的表达，犳狑是聚合函数，其在文章中被定义成递归函数，根据犳狑迭代更新节点狓的表达直到收敛．此外，图神经网络定义全局输出函数并作用在收敛后每个节点的表达上得到最终输出结果，我们用犵狑表示全局输出函数，最终结果为（１８）　　近期，注意力机制引起广泛关注，图注意力网络（ＧＡＴ）［２８］正是通过注意力机制定义聚合函数，但是和以往关心边上信息的模型不同，在图注意力网络中，邻接矩阵仅被用来定义相关节点，而关联权重的计算则是依赖节点的特征表达．图注意力网络每一层的结构如图４所示，图４（ａ）以节点犻，犼的特征表达作为输入，计算犻，犼之间的注意力权重并归一化，图４（ｂ）利用注意力权重将周围节点的表达以加权和的形式聚合到自身，对于多种注意力机制下的计算结果，图注意力网络提供了拼接和均值两种计算方式．注意力权重和表达更新的计算公式分别如下 α犻，犼＝ｅｘｐ（ＬｅａｋｌｙＲｅＬＵ（犪［犠犺犻‖犠犺犼］））， ∑犽∈犖（犻）ｅｘｐ（ＬｅａｋｌｙＲｅＬＵ（犪［犠犺犻‖犠犺犽］））犺犻＝σ∑犼∈犖（犻）α犻，犼犠犺（）犼（１９）其中，参数犠用于完成每个节点的特征维度变换，参数犪用于计算节点间的注意力权重，‖表示向量拼接，α犻，犼表示在犪下计算得到的犻，犼节点间的权重， σ表示非线性激活函数．《计算机学报》

２６７计　　算　　机　　学　　报２０２０年此外，ＤＣＮＮ［３０］利用随机行走后得到的犓跳转移概率定义节点间的权重，第犿层的结构如下：犎犿＋１＝犺（犘犓犎犿犠）（２０）其中，犘犓表示两个节点在随机行走下犓跳可达概率，犠是需要学习的参数．此类模型刻画了节点之间的高阶信息，但是由于犘犓的计算复杂度为犗（狀２犓），难以扩展到大图上．不同于以往认为节点只属于唯一标签的方法，基于置信度的图卷积网络（ＣｏｎｆＧＣＮ）［３１］认为节点是以一定的置信度为一个标签，因此ＣｏｎｆＧＣＮ给每个节点学习置信度函数，并将其作用在节点相关性上，修正聚合函数．图６给出了ＣｏｎｆＧＣＮ在应用到节点二分类问题上的结构，在置信度作用后的聚合函数上，异配连接更容易被识别出来，进而降低相关系数．超图卷积网络（ＨＧＮＮ）［３２］则认为节点间的相关性不应该是节点两两之间产生，而是一组节点相互影响进而构建组内节点相关性．基于此想法，ＨＧＮＮ将边拓展到连接多个节点的超边，在超边上定义聚合函数进行节点特征传播．图４　图注意力网络结构［２８］（（ａ）利用注意力机制计算两个节点之间的权重；（ｂ）根据计算的权重更新目标节点）从图注意力网络开始，节点之间的权重计算开始从依赖于网络的结构信息转移到依赖于节点的特征表达，但是以上模型在处理时需要加载整个网络的节点特征，这阻碍了模型在大规模网络上的应用．基于此，Ｈａｍｉｌｔｏｎ等人［２９］提出图采样聚合网络（ＧｒａｐｈＳＡＧＥ），不同于以往模型考虑所有邻近节点，图采样聚合网络对邻近节点做随机采样，使得每个节点的邻近节点都小于给定的采样个数．图采样聚合网络的结构如图５所示．图５　图采样聚合网络结构［２９］（（ａ）以每个节点为中心，对其邻近节点采样；（ｂ）利用采样节点更新目标节点的表达；（ｃ）利用更新后的节点表达预测节点的Ｌａｂｅｌ）以红色节点为目标节点，图采样聚合网络首先对其一阶邻居和二阶邻居做随机采样，并仅把采样到的节点作为相关节点，然后，模型将聚合函数作用在相关节点的特征表达上，并用聚合结果更新红色节点的特征表达来完成对应任务．此外，图采样聚合网络给出多种聚合函数的形式，分别是基于最大值的聚合，基于均值的聚合和长短时记忆力网络（ＬＳＴＭ）．最大值聚合和均值聚合分别指取相关节点的最大值和均值作为聚合结果；长短时记忆网络指将相关节点输入ＬＳＴＭ，并把输出作为聚合结果．图采样聚合网络也提出用分批量（Ｍｉｎｉｂａｔｃｈ）处理数据的方法训练模型，在每个批量输入数据下只需要加载对应节点的局部结构，避免了整张网络的加载，这使得在大规模数据集上搭建图卷积神经网络成为可能．图６　基于置信度的图卷积网络［３１］以上基于聚合函数的空间方法着眼于空间方法中的根本问题，即聚合函数的构造．随着图卷积神经网络的发展，研究人员开始考虑更复杂的场景，并涌现出一类建模信息更为丰富的空间方法，包括如何在具备连边信息的网络上搭建图卷积神经网络，如何建模高阶信息等，我们在第４节对这类空间方法做详细介绍．（３）深度理解图卷积网络上文已经介绍了图卷积神经网络的通用框架和建模方法，在这一节中，我们将分析图卷积模型的内部机制及不同模型的建模能力．Ｌｉ等人［４５］在图卷积神经网络的协同训练（Ｃｏ ＴｒａｉｎＧＣＮ）一文中对一阶图卷积神经网络（ＧＣＮ）展开详细分析，并指出ＧＣＮ的本质是拉普拉斯平滑．Ｌｉ等人指出单层的ＧＣＮ也显著优于全连接网络（ＦＣＮ），而ＦＣＮ和ＧＣＮ的区别仅在于式（１３）中《计算机学报》

分享到：

赞收藏

资料库

《图卷积神经网络》中文综述论文.pdf

相关推荐

人工智能

热门标签

最新资料