IEEE ANTENNAS AND WIRELESS PROPAGATION LETTERS, VOL. 6, 2007 553 Joint SVD of Two Cross-Correlation Matrices to Achieve Automatic Pairing in 2-D Angle Estimation Problems Jian-Feng Gu and Ping Wei, Member, IEEE Abstract—Recently, Kikuchi et al. proposed a pair-matching method for two-dimensional (2-D) angle estimation using a cross-correlation matrix. Unlike some classical pair matching methods which require a complex process, Kikuchi’s Method uti- lizes the corresponding combinations of the elevation and azimuth angles emerging in the cross-correlation matrix of two uniform linear arrays (ULAs) to achieve automatic pairing. However, Kikuchi’s method has some drawbacks such as the pair matching and failure problems when the difference of the corresponding combinations of the 2-D angles cos =1 is small and the signal-to-noise ratio (SNR) is low. Furthermore, this method does not make good use of the cross correlation, where the effect of additive noise is eliminated, to improve the estimation performance. We propose a novel automatic pairing scheme for es- timating 2-D angle by simultaneous singular value decomposition (SVD) of two cross-correlation matrices. Computer simulation results are presented to show that the proposed technique can overcome these problems and offer better estimation performance. Index Terms—Automatic pairing, cross-correlation matrix, joint cos SVD, two-dimensional (2-D) angle. I. INTRODUCTION THE two-dimensional (2-D) direction-of-arrival (DOA) estimation using a 2-D array of sensors has received considerable attention in the recent array signal processing literature. Much research has been done based on the uniform rectangular array (URA) [1]–[3] because the URA can be re- garded as the 2-D extension of the uniform linear array (ULA). However, these methods need a number of sensors to achieve high resolution and give accurate estimates. It has been proven in [4] that the L-shaped array has better estimation performance than many other simple structured arrays. More recently, there has been growing interest in developing 2-D angles estimators by exploiting the L-shaped arrays [5]–[7]. Tayem and Kwon [6] presented a computationally simple 2-D DOA estimation with propagator method using one or two L-shaped arrays. However, this method may cause the pair matching and failure problems [7]. Consequently, Kikuchi et al. [7] proposed a pair-matching method to remove the aforesaid problems using a cross-correlation matrix. The Kikuchi’s method still has several drawbacks: 1) it will cause the pair matching problems when the difference of the corresponding Manuscript received December 5, 2006; revised August 21, 2007. The authors are with the Department of Electronic Engineering, University of Electronic Science and Technology of China, Chengdu, Sichuan 610054, China (e-mail: Gujianfeng@uestc.edu.cn; Pwei@uestc.edu.cn). 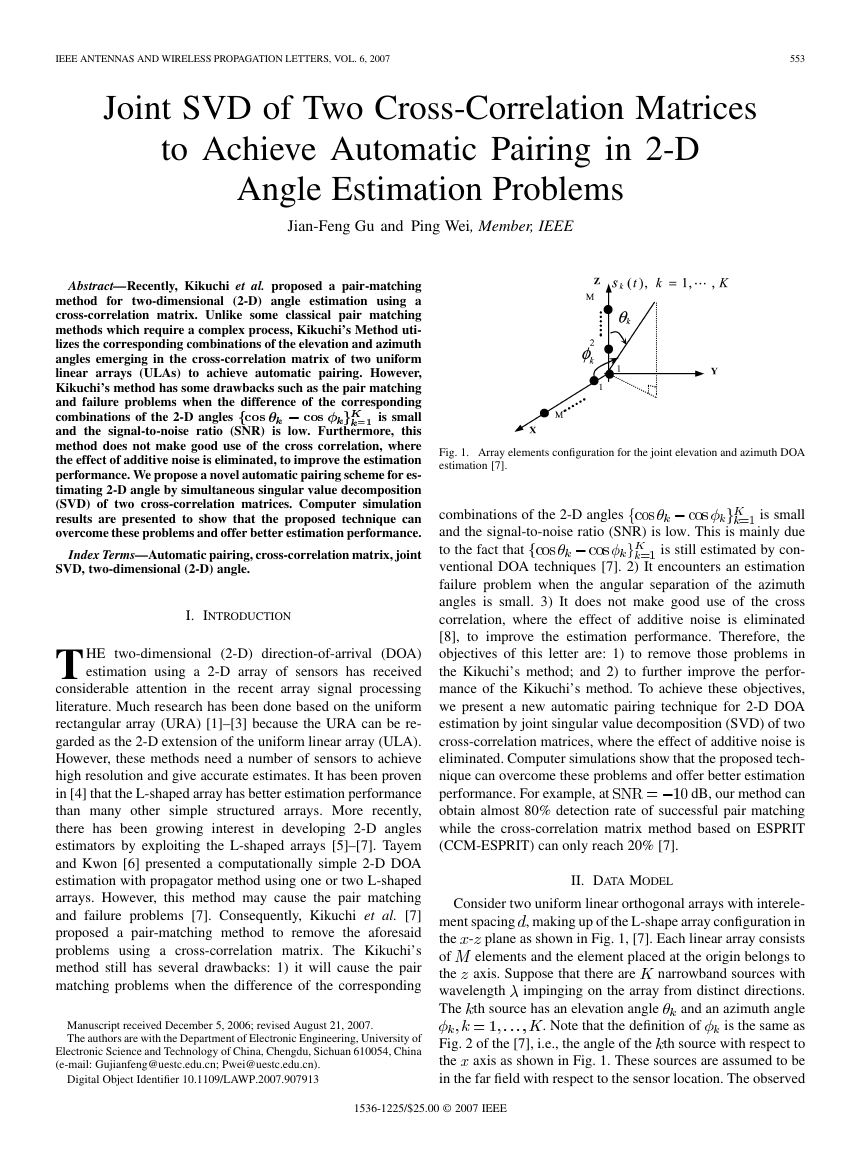Digital Object Identifier 10.1109/LAWP.2007.907913 Fig. 1. Array elements configuration for the joint elevation and azimuth DOA estimation [7]. combinations of the 2-D angles is small and the signal-to-noise ratio (SNR) is low. This is mainly due is still estimated by con- to the fact that ventional DOA techniques [7]. 2) It encounters an estimation failure problem when the angular separation of the azimuth angles is small. 3) It does not make good use of the cross correlation, where the effect of additive noise is eliminated [8], to improve the estimation performance. Therefore, the objectives of this letter are: 1) to remove those problems in the Kikuchi’s method; and 2) to further improve the perfor- mance of the Kikuchi’s method. To achieve these objectives, we present a new automatic pairing technique for 2-D DOA estimation by joint singular value decomposition (SVD) of two cross-correlation matrices, where the effect of additive noise is eliminated. Computer simulations show that the proposed tech- nique can overcome these problems and offer better estimation dB, our method can performance. For example, at obtain almost 80% detection rate of successful pair matching while the cross-correlation matrix method based on ESPRIT (CCM-ESPRIT) can only reach 20% [7]. II. DATA MODEL Consider two uniform linear orthogonal arrays with interele- ment spacing , making up of the L-shape array configuration in the - plane as shown in Fig. 1, [7]. Each linear array consists elements and the element placed at the origin belongs to of axis. Suppose that there are narrowband sources with the wavelength impinging on the array from distinct directions. and an azimuth angle The th source has an elevation angle is the same as Fig. 2 of the [7], i.e., the angle of the th source with respect to the axis as shown in Fig. 1. These sources are assumed to be in the far field with respect to the sensor location. The observed . Note that the definition of 1536-1225/$25.00 © 2007 IEEE 

554 IEEE ANTENNAS AND WIRELESS PROPAGATION LETTERS, VOL. 6, 2007 signals at the subarray along the the axis are given by axis and the subarray along denotes a matrix consisting of the th to the th columns of matrix . We obtain the relationship The matrices and vectors in (1) and (2) have the following forms: where into (6) yields (1) (2) (7) and . Substituting (7) Then we can verify that (8) can be rewritten as Define a new and in the form matrix by concatenating (3) The singular value decomposition (SVD) of yields where and where the superscripts denote the axis subarray and noises in the tively. In addition, vector of source signals, denote the transpose, axis subarray, respectively, axis subarray and and and th element of the received data in the is the and are additive axis subarray, respec- denote the array response matrices (vectors) in the axis axis subarray, respectively. It is also assumed are uncorrelated each other and the additive are independent of the signal samples are white Guassian random subarray and that the sources noises [7]. The elements of processes with zero-mean and variance . It can be verified that III. PROPOSED METHOD We obtain a cross-correlation matrix between the signal vectors and as follows Since leads to the relationship is of full rank, (12) implies (8) (9) (10) (11) (12) . This (13) (4) Hence, there exists a nonsingular matrix such that where th source. The superscript and is the power of the denotes the conjugate transpose. is From (4), we can see that the cross-correlation matrix not affected by the additive noise. Next, let us partition the cross-correlation matrix into two matrices of the size such that (5) (6) where of the array response matrix and denote the first and last rows axis. The notation in the And we can decompose into two matrices such that (14) and (15) Equation (15) establishes the one-to-one relationship be- tween the signal subspace of the azimuth angles and the rotationally invariant counterpart of the elevation angles. Unlike the traditional ESPRIT, this rotational invariance is obtained without requiring translational invariance of the array. 

GU AND WEI: JOINT SVD OF TWO CROSS-CORRELATION MATRICES 555 Hence, the array geometry of to a ULA. axis is not necessarily restricted Having obtained this invariance, we can follow the same pro- . From (15), cedure of the standard ESPRIT [9] to estimate we have and This implies that relationship (16) (17) and gives rise to the (18) where tion of diagonal elements of the matrix finding the denotes the Moore-Penrose pseudo-inverse. Estima- can be obtained by . Thus, the elevation angle eigenvalues of for each source can be found as (19) Moreover, since eigenvectors of , we can obtain an estimation of the array response makes up of the matrix as We then use the “beamforming-like” method to obtain an esti- mate of the azimuth angle (21) where denote the th column of . IV. SIMULATION RESULTS In this section, we present some numerical examples to evaluate the estimation performance of the proposed method and the cross-correlation matrix method based on ESPRIT (CCM-ESPRIT) [7]. In all examples, we consider an L-shaped apart for array as shown in Fig. 1 with elements space each ULA. The number of sensors is and the number . Additionally, results shown below of snapshots is are obtained from Monte Carlo simulation based on 1000 independent realizations of the received data. 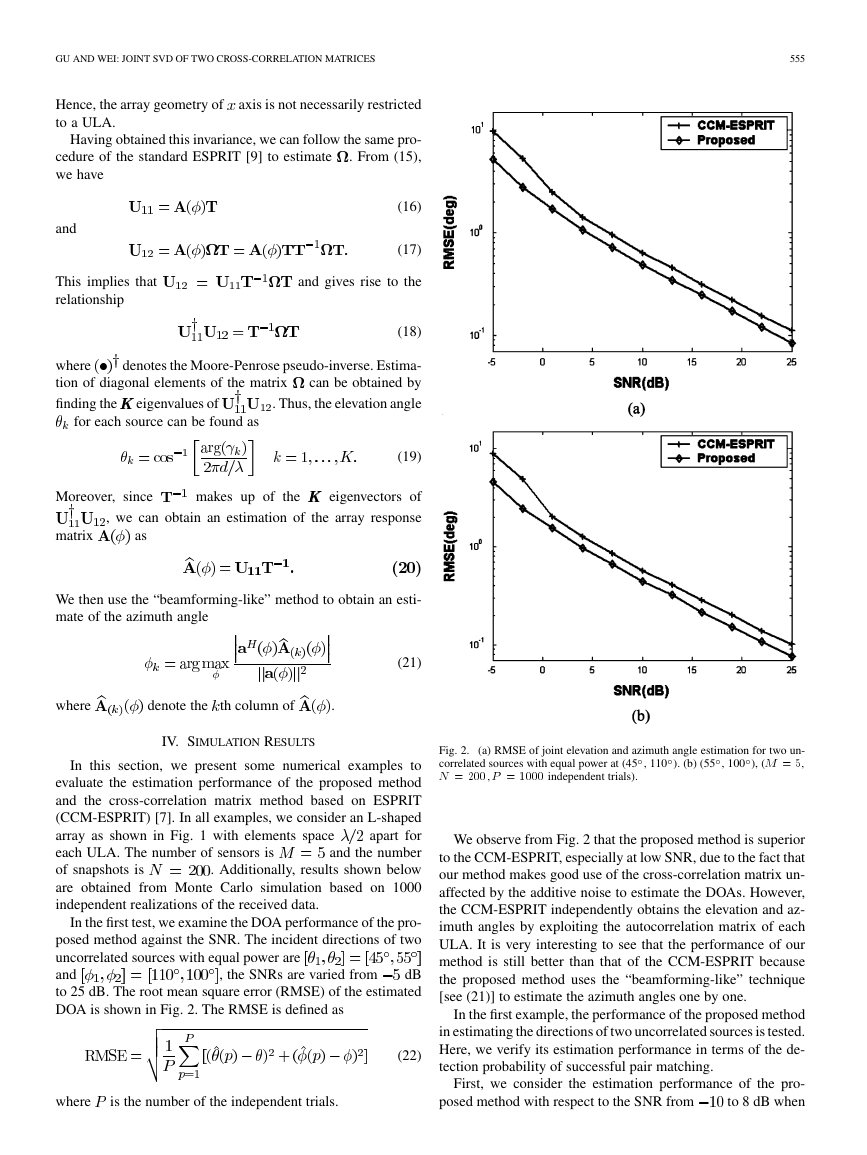In the first test, we examine the DOA performance of the pro- posed method against the SNR. The incident directions of two uncorrelated sources with equal power are and dB to 25 dB. The root mean square error (RMSE) of the estimated DOA is shown in Fig. 2. The RMSE is defined as , the SNRs are varied from (22) where is the number of the independent trials. Fig. 2. (a) RMSE of joint elevation and azimuth angle estimation for two un- correlated sources with equal power at (45 , 110 ). (b) (55 , 100 ), (M = 5; N = 200; P = 1000 independent trials). We observe from Fig. 2 that the proposed method is superior to the CCM-ESPRIT, especially at low SNR, due to the fact that our method makes good use of the cross-correlation matrix un- affected by the additive noise to estimate the DOAs. However, the CCM-ESPRIT independently obtains the elevation and az- imuth angles by exploiting the autocorrelation matrix of each ULA. It is very interesting to see that the performance of our method is still better than that of the CCM-ESPRIT because the proposed method uses the “beamforming-like” technique [see (21)] to estimate the azimuth angles one by one. In the first example, the performance of the proposed method in estimating the directions of two uncorrelated sources is tested. Here, we verify its estimation performance in terms of the de- tection probability of successful pair matching. First, we consider the estimation performance of the pro- to 8 dB when posed method with respect to the SNR from 

556 IEEE ANTENNAS AND WIRELESS PROPAGATION LETTERS, VOL. 6, 2007 of the azimuth angles is small. Therefore, the separation detection probability of CCM-ESPRIT is low at small angular separation. However, our method will remove the failure prob- lems when estimating the azimuth angles due to the fact that each azimuth angle is obtained by the “beamforming-like” scheme independently while CCM-ESPRIT exploits the tra- ditional ESPRIT [9] to estimate the DOAs. Furthermore, the detection probability of CCM-ESPRIT is very low due to the fact that the Toeplitz matrix in [7] is a singular matrix when while the detection probability of our method will be unaffected in such cases. V. CONCLUSION In this letter, we have presented a new automatic pairing method for estimating 2-D directions of wave arrival using an L-shaped array. The proposed method exploits the property of the L-shaped array to obtain two cross-correlation matrices, where the effect of additive noise is eliminated. Then we use the joint SVD technique to achieve automatic pairing and offer good estimation performance. Simulation results show that the proposed scheme not only provides better estimates than CCM-ESPRIT does, especially at low SNR, but also works well at low SNR or small angular separation situations. For example, the RMSE of CCM-ESPRIT is about 30% (even 50% at SNR less than 0 dB) higher than that of the proposed method (Fig. 2). And our method can still obtain almost 100% detection rate while the detection probability of the CCM-ESPRIT is dB (Fig. 3). Moreover, the detection under 50% at probability of the CCM-ESPRIT is almost 0% when the angular to 12 , whereas the proposed difference method is still 100% detection rate (Fig. 4). In addition, the proposed method can use the arbitrary array geometries in the x-y plane although the ULA in the axis is adopted throughout the letter. lies between REFERENCES [1] A. Swindlehurst and T. Kailath, “Azimuth/elevation direction finding using regular array geometries,” IEEE Trans. Aerosp. Electron. Syst., vol. 29, no. 1, pp. 145–156, 1993. [2] M. D. Zoltowski, M. Haardt, and C. P. Mathews, “Closed-form 2-D angle estimation with rectangular arrays in element space or beamspace via unitary ESPRIT,” IEEE Trans. Signal Process., vol. 44, no. 2, pp. 316–328, 1996. [3] P. Strobach, “Two-dimensional equirotational stack subspace fitting with an application to uniform rectangular arrays and ESPRIT,” IEEE Trans. Signal Process., vol. 48, no. 7, pp. 1902–1914, 2000. [4] Y. Hua, T. K. Sarkar, and D. D. Weiner, “An l-shaped array for esti- mating 2-D directions of wave arrival,” IEEE Trans. Antennas Propag., vol. 39, no. 2, pp. 143–146, 1991. [5] J. E. Fernandez del Rio and M. F. Catedra Perez, “The matrix pencil method for two-dimensional direction of arrival estimation employing an L-shaped array,” IEEE Trans. Antennas Propag., vol. 45, no. 11, pp. 1693–1694, 1997. [6] N. Tayem and H. M. Kwon, “L-shape 2-dimensional arrival angle esti- mation with propagator method,” IEEE Trans. Antennas Propag., vol. 53, no. 5, pp. 1622–1630, 2005. [7] S. Kikuchi, H. Tsuji, and A. Sano, “Pair-matching method for esti- mating 2-D angle of arrival with a cross-correlation matrix,” IEEE An- tennas Wireless Propag. Lett., vol. 5, pp. 35–40, 2006. [8] J. Xin and A. Sano, “Computationally efficient subspace-based method for direction-of-arrival estimation without eigendecomposition,” IEEE Trans. Signal Process., vol. 52, no. 8, pp. 876–893, 2004. [9] R. Roy and T. Kailath, “ESPRIT-estimation of signal parameters via rotational invariance techniques,” IEEE Trans. Acoust., Speech, Signal Process., vol. 37, no. 7, pp. 984–995, 1989. Fig. 3. Detection probability verses SNR for two uncorrelated sources with equal power at (45 , 110 ) and (55 , 100 ) (M = 5; N = 200; 1000 inde- pendent trials). Fig. 4. Detection probability verses angular difference separation for two un- correlated sources with equal power with SNR = 5 dB (M = 5; N = 200; 1000 independent trials). two equal power uncorrelated sources arrive from and . The detection prob- ability of successful pair matching obtained by the proposed method and the CCM-ESPRIT are depicted in Fig. 3. The re- sults indicate that, for low SNR, the success rate of the proposed method is higher than that of the CCM-ESPRIT. In particular, at dB, our method can obtain almost 80% detection rate while the CCM-ESPRIT can only reach 20%. Furthermore, the performance of the proposed method is studied in terms of the angular difference between the az- imuth angles of two equal power uncorrelated sources. In this example, two sources impinge on the L-shaped array along , where . Fig. 4 shows the detection probability of successful pair matching of the proposed method and the CCM-ESPRIT against the angular , where the SNR is set at 5 dB. Because the difference CCM-ESPRIT estimates the 2-D DOAs by the auto-correlation will fail when the angular matrix, the DOA estimation of is varied from and to