第35卷第3期 2006年 6月 信 息 与 控 制 Information and Control Vol. 35， June, No. 3 2006 文章编号 :1002-0411(2006) 03-0294-05 基于支持向量机的代价敏感挖掘 (1.中国计量学院机电工程学院，浙江 杭州 310018; 2.浙江大学工业控制技术研究所，浙江 杭州 310027) 郑恩辉‘,2，李 平，，宋执环“ 摘 要:针对一些数据挖掘应用中反例样本和正例样本具有不同误分类代价的情况，提出一种代价敏感 支持向量机算法CS-SVM. CS-SVM包括3个步骤:首先，引入Sigmoid函数，根据样本到分类超平面的距离估 计其后验概率;然后，根据误分类代价最小原则重构训练样本的类标号;最后，在重构后的训练集上使用标准 SVM进行学习即得到嵌人误分类代价的最优分类超平面.基于 CS-SVM的思路，提出一个通用的嵌人误分类 代价的代价敏感分类算法 G-CSC.试验结果表明:相比于 SVM, CS-SVM大大降低测试集上的平均误分类代 价. 关键词 :分类 ;支持向量机 ;代价 中图分类号:TP181 文献标识码:A SVM-based Cost Sensitive Mining ZHENG En-hui''2，LI Ping2，SONG Zhi-huan2 (1. College of Mechatronics Engineering, China Jiliang University, Hangzhou 310018，China; 2. Institute of Industrial Control Technology，Zhejiang University, Hangzhou 310027，China) Abstract:A cost-sensitive support vector machine(CS-SVM) algorithm is proposed for the error cost of positive class samples being generally unequal to that of negative class sample in some applications of data mining. The con- struction of CS-SVM algorithm consists of three steps. Firstly, the post probability of each sample in training set is es- timated based on sigmoid function and the distance of each sample to the optimal separate hyper-plane. Secondly, the label of each sample in training set is reconstructed to minimize misclassification cost of each sample. Finally, we can learn the misclassification cost-sensitive hyper-plane using SVM algorithm and the reconstructed training set. On the basis of CS-SVM, a general cost-sensitive classification(G-CSC) algorithm wrapping different misclassification costs of each class sample is proposed. Experimental results show that CS-SVM greatly reduces the average misclassification cost. Keywords:classification; support vector machine(SVM );cost 1 引言(Introduction) 为摆脱“数据丰富”和“知识贫乏”的境地，数据 挖掘(data mining, DM)正得到越来越多的研究{‘〕. 分类是DM的重要内容，现有分类算法(如判定树和 神经网络等)大多假定每个样本的误分类具有同样 的代价而致力于提高分类器的泛化精度〔‘〕。但对很 多现实的DM问题，不同样本的误分类代价通常不 相等，仅凭全局精度评价分类器的性能优劣是不够 的[2-41.在极端情况下，不考虑样本的不同误分类代 价而建立的模型没有任何意义.以医疗诊断为例，把 “病人”误诊为“健康人”的代价和把“健康人”误诊 为“病人”的代价是不同的.前者使“病人”失去治疗 的机会，以病情恶化或生命为代价，后者以再次诊断 或药物的副作用为代价，显然前者误分类代价要大 于后者.若样本集包含 2个“病人”和98个“健康 人”，分类器通过把所有样本划分为“健康人”即可 得到98%的分类精度，但这样的诊断不能识别出 “病人”，没有实际意义.对此类问题，须引人代价敏 感挖掘(cost sensitive mining, CSM)进行建模和预 测.CSM是普适机器学习所面临的挑战，在中国鲜 有报道[，:. CSM的研究集中在以下两类方法:其一，重构 收稿 日期 基金项 目 2006一01一27 国家 863计划资助项 目(2002AA412010-12 ) 

3期 郑恩辉等 :基于支持 向量机的代价敏感挖掘 训练集，然后使用现有的算法实现 CSM;其二，重新 设计分类器，使分类器本身具有代价敏感性.对第一 类方法，最初重构训练集的方法是:根据样本的不同 误分类代价，复制样本集的正例样本或删除反例样 本，其缺点是丢失部分有用样本的信息或增加计算 和存储开销，且复制正例样本易引起过学习.文[4] 给出了增加样本集中正例、重构训练集的方法，研究 了基率改变对贝叶斯学习及决策树生长和剪枝的影 响.第二类方法直接设计代价敏感分类器.文【3〕依 据代价，把代表重要性的权值集成进AdaBoost，在第 一次迭代中按此权值进行采样.文「5〕通过把一个 误分类函数引人到权值的重构 中对文 「3]进行扩 展，允许每个样本有不同的误分类代价. 本文的研究属于第一类方法，根据标准 SVM的 训练结果，引人概率估计和代价最小化过程，赋予每 个样本一个新的类标号，然后重新使用标准SVM实 现 CSM.该方法使用训练集的全部样本，重构后的 样本集的类标号蕴含了样本的误分类代价信息.以 上方法i1il练的分类器为代价敏感SVM (cost sensitive SVM , CS-SVM ).文[6」基于结构风险最小化原则提 出代价敏感支持向量机的设计，但考虑的代价类型 为拒识代价;文「7」中的代价敏感支持向量机考虑 的是误分类代价，但是通过给不同类别的经验风险 赋予不同的权值直接改进标准 SVM. 2 支持向量机(Support vector machines) SVM是一种强大的机器学习和数据挖掘算 法〔6].和传统算法基于经验风险最小化准则(empiri- cal risk minimization, ERM)不同，SVM使用结构风 险最小化(structural risk minimization, SRM)准则构 造决策超平面，平衡模型复杂度和经验风险，提高学 习算法的泛化能力. 对两类问题，假定己知观测样本集 (XI 'Yi)，…，(xi 'Yi)，…，(xn " Yn) xi E R'，，:E{+1，一1}，i=1，…，。 (1) 能被超平面(w·x)一b =0分类 ，其中 l为样本(预 测属性)的维数，n为样本的数量，Y‘为样本x、的类 别(目标属性).学习问题为最小化 目标函数 R(w，若)=音}}w 112+C(艺ei) (2a) s. t. Yt ( xc· ei)0， w+b) > 1一61 (2b) 其中，Ilwll，代表模型的复杂度，6、为松弛变量， = 1，… ,n (艺若、)为经验风险，C为松弛因子. 通过构造拉格朗日方程，并转化为对偶形式，优 化问题(2)的解为最优决策超平面(optimal decision hyper-plane，ODH)为f(x) =艺yj+i (x·x;)+b=0， sv 可重写为: f(x)=wo·x+b=0 (3) 其中。;}-> 0，为拉格朗日系数，a, > 0所对应的样本 称为支持向量(support vector, SV ) , SVM的ODH只 依赖于SV，即SVM的解具有稀疏性.以上为线性情 况.对非线性情况，依据Cover定理[8]，使用核函数 K(x;,xi)代替(x='xi)即可得到非线性情况下的 ODH，b依KKT条件确定[“]. 3 基于 SVM 的代价敏感挖掘 (SVM-based CSM) 基于贝叶斯决策论的启发，本部分给出 CSM的 一个实现框架，提出CS-SVM算法，进而提出一个通 用的代价敏感分类算法G-CSC. 3.1 贝叶斯决策论及其启发 设任一样本x属于类1的概率为P (.i I x )，贝叶 斯决策论把该样本分类为 i需最小化条件风险 R(ilx)=艺P(jlx)C(i，J) (4) 最小化后的条件风险称为贝叶斯风险.其中i, j E }。，，。:，…，。。},m表示类别数;C(i,，’)表示把一个J 类样本分类为 i的风险，i=j表示正确的分类，i=Aj 表示错误的分类.对基于精度的“0-1”损失分类器，i =j时，C(i, j)二0,ioj时，C(i, j)二1，分类的任务 是寻找x的极大后验概率. 然而，对于 CSM问题，ioj时，C(i, j) OC(j, i).此时不能只依靠x的极大后验概率确定其类别. 不难发现，若给定把一类样本误分为另一类的代价， 可重新构造代价矩阵 C，基于框架(4)式实现 CSM 任务，使全局误分类代价最小.其中，代价 C(i, j)可 以是财产的损失、时间的损耗等，也可用收益替代代 价. 实际上，若把样本空间分为多个区域，每个区域 对应一个类别，则分类任务转化为寻找类和类之间 的边界.以两类分类问题(正例类 p和反例类 n, P(川x)二1一P(nIx))为例说明 CSM的本质和实 现方法.基于精度最优的标准分类任务假定每类样 本的误分类代价相等，即C(p,n) =C(n,p)，我们只 关注P(川x)就足够了，依 P(川x) =0.5确定分类 边界，若 P(川 x) =0.3，则 xen.但对 CSM问题， C(p,n) 0C(n,p)，不妨设置代价矩阵为 C (p, n) = 

信 息 与 控 制 35卷 1,C(n,p)二4,C(p,p)=C(n,n)=0，此时若P(p}x) =0.3(对应 P(n} x) =0.7)，那么依式 (4)得 R(p}x) =0.7,R(n}x)=1.2，根据 CSM最小误分类 代价最小的要求，xep.此时应依P(川x) =0.2确 定分类边界，即分类边界靠近误分类代价较小的类 n样本，进人类 n样本的内部.因此，CSM的本质是 寻找样本的真实类标号(使误分类代价最小)，而不 是它更可能属于哪一类(属于某类的概率较大). 3.2 CS-SVM 给定代价矩阵 C, (4)式为实现 CSM的一个框 架.以下基于标准 SVM，通过引人概率估计和代价 最小化过程重构训练集，提出 CS-SVM算法，并在此 基础上提出 G-CSC算法. 3.2. 1 CSM问题描述 给定代价矩阵C(i, J)和样本集x (xi,Yi)，… x; , Yi)，…，('xn ,Yn) xi e RZ，Yi {Cl ,C2 ，…,Cm} (5) 其中，n为样本数，m为样本的类别数，l为样本预测 属性的维数.CSM的任务是设计一个分类器，使其 对给定的 x和 C，实现误分类代价最小.以上为 CSM问题的描述，和基于精度的算法在样本集 x上 进行学习不同，CSM在样本集 x和代价矩阵 C上进 行学习，以误分类代价最小为 目标.显然，基于精度 的算法是 CSM算法的特例. 3.2.2 概率估计 假设已知代价矩阵 C，依框架(4)进行 CSM需 要估计后验概率P(JI X).贝叶斯分类器可以直接给 出该概率，但它关于类条件独立的假定缺乏准确性， 而且缺乏可用的概率数据，这都影响了实际应用效 果;神经网络尽管可以实现含噪的高度非线性映射， 但网络结构的确定没有严格的理论基础，且存在过 学习问题[’〕.本文采用有严格理论基础的SVM估计 后验概率.对样本集(1)的两类分类问题，采用样本 x到超平面(3)的距离信息d(x) (d(x) E R)并引人 Sigmoid函数计算后验概率P(JI X).计算方法如下: P(1 Ix) 1 1+exp(一a·d(x)) (6) 其中，。为 Sigmoid函数的参数，P(j 一lax)二 1一P(j=11x). 3.2.3 代价最小化 对训练集中的每个样本 x，先估计后验概率 的 P(j I x)，然后根据(4)式计算其属于任意一类 代价 ，根据 - ， ‘ 夕=arg min{R(iIx)} 2 吸 、 、 ， 尹 7 重构训练样本集的类标号为夕，该类标号集成了样 本的误分类代价信息，称为样本的“真实”类标号. 对样本集(1)给定的两类问题，只要比较 R(-1 I x) 和R(lix)的大小即可. 3.2.4 代价敏感支持向量机 根据 CSM的本质，样本集(5)依代价矩阵 C被 重构为X (x,，夕，)，…，(x;，夕‘)，…，(x,，又) xi。Rn，又 二}c, , c2，…,cm}，i=1,2，…,l (8) 样本集X集成了样本的误分类代价信息，使用基于 精度的算法在样本集(8)上进行学习，得到的分类 器称为代价敏感分类器(cost-sensitive classifier, CSC).对两类问题，使用标准 SVM分类算法得最优 分类超平面 六x)=wo·x+瓦=0 (9) 相应的决策函数为: 大(x)=sign( w.·x+Eo) (10) 我们定义式(9)为代价敏感 ODH ( cost-sensitive ODH, CS-ODH )，定义式(10)为代价敏感 ODF ( cost- sensitive ODF, CS-ODF).其中，w。和凡分别表示 CSM问题中的最优权值和最优偏置. 以上，提出了样本误分类代价不相等时支持向 量机的设计过程，它集成了样本的误分类代价信息， 称之为代价敏感支持向量机(cost sensitive SVM, CS- SVM). CS-SVM和 SVM的不同之处是:(1)由于引 人了代价矩阵 C, SVM 中具有同样拉格朗 日系数的 样本x‘在 CS-SVM中可能表示不同类型的SV;(2) CS-ODH比ODH靠近误分类代价小的反例样本，降 低误分类代价小的反例样本的分类精度，保证误分 类代价高的正例样本获得较高的分类精度;(3)尽 管全局泛化精度降低，即误差率有所提高，但平均测 试集误分类代价大大降低. 表 1 G-CSC算法 Tab. 1 G-CSC algorithm 算法:通用代价敏感分类(G-CSC)算法 输人:分类算法CA1和CA2;如(5)式的训练样本集X;代价矩阵C 输出:代价敏感分类器(CSC) 方法 : 1)for i 二1,2, ‘二 ,n 2) 3) 4) for j = 112,---,m P(cj Ixi)Gg(CA1,X); //由X和CA1计算第i个样本属于类CJ的概率 5 ) fork=1 ,2，…，n 

3期 郑恩辉等:基于支持向量机的代价敏感挖掘 车 军 羁 除 月 料 坦 燕 侧 国 奋 叩 5 切 显 国 补 5 猛 划 拟 卞 月 戳 坦 民 担 层 补 甲 5 卿 显 芝 补 5 毅 划 拟 众 月 辫 催 晨 担 芝 淤 叩 5 晶 芝 争 的 0.95 ” 0.85 0.8 0.75 0.7 0.65 0.6 0.55 0.5 0.45 ， 且 Q 夕 0 丹 ， . ‘ 、 户 … … n U 0 0 介 U O 介 U ‘ q 6) 7) 8) 9) 1 0 1 . 1 1 工 、 I J J 、 ， . J for i, j二1,2,…，m R(iIx)二艺P(jIX)C(i>j); 久 二argminIR(iIxk)}; //得到重构后的样本集A CSCGg(CA2，夕); //由分和给定的CA2，得到CSC 以上推导的 CS-SVM适用于两类问题，对多类 问题可通过逐一鉴别法(one-against-the-rest me- thod)和一一区分法(one-against-all method)转换为 多个两类问题进行求解.需要指出的是:(1)分类算 法 CA 1可以用任意的分类算法替换，只要其输出为 后验概率p(JI x)的形式或可以转化成后验概率的 形式;(2) CAI和CA2可以是不同类型的分类算法. 我们不妨称推广后的算法为通用代价敏感分类 (general cost sensitive classification, G-CSC)算法，表 1给出了G-CSC算法的伪代码. 4 数值试验结果(Results of numerical test) 试验使用两个包含代价矩阵的Benchmark数据 集 German Credit和Heart Disease，两个数据集的符 号属性被转换为整型，样本数较少的“欺诈”和“病 人”类别为正例类 1，相应的另一类别为反例类 一1. German Credit数据集[9]包括300个正例和700个反 例，每个样本有 24个预测属性和 1个 目标属性. Heart Diseas。数据集[9]包括120个正例和150个反 例，每个样本有 13个预测属性和 1个 目标属性.两 个数据集的代价矩阵同为:C(l,1)二C(一1，一1) =0,C(1，一1)=1,C(一1,1) =5.在每个数据集 上，取20次试验的均值，每次随机选择一定数目的 样本组成训练集，其余的样本为测试集.图 1和图2 为部分试验结果. 1.1一 车 军 软 除 叫 戮 牲 展 彬 居 淤 叩 S Q 显 国 补 5 ‘. 9 8 7 ‘ U n U 0 0 0 0 5 0 4 ..a...AV 一C 一-+- CS -AV-C 口 包 百 口 口 。 a 100 训练(子)样本集大小 Heart 口 口 . 一 山 ， - 0 J 旧 l es es es es 泊 es es es es J O 口 ， a . 曰 曦 口 钱 口 . 0 50 厂 比 1一n'只 。 口 AV 一C 一，一CS-AV 一C ‘、石o’ a.v。卜口1 3- 口牙以口 口 0.8- 0.7一从 _ 0. 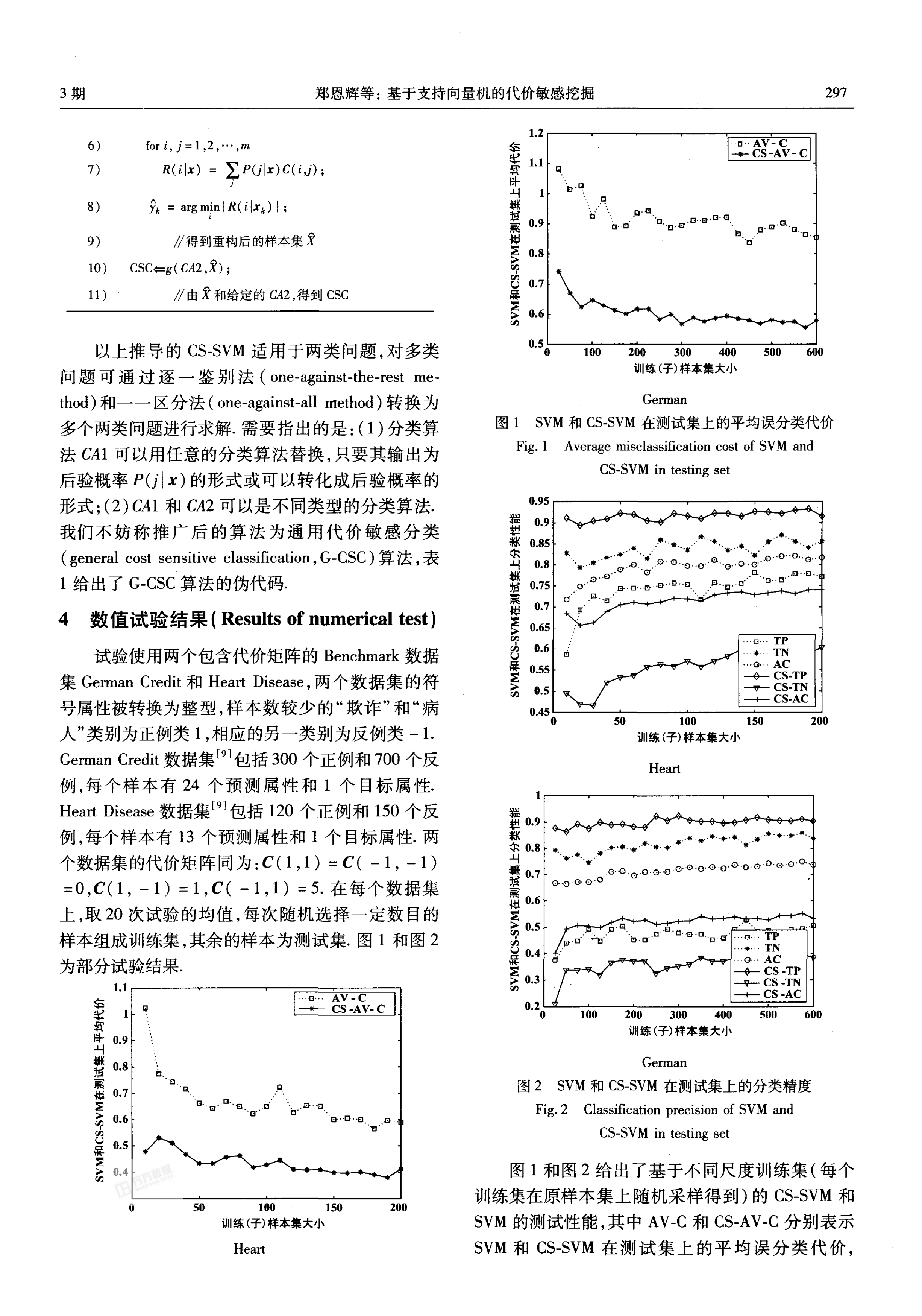一 ~洲产 \ -A - __ _ .、丫滩， 神 200 300 400 训练 (子)样本集大小 500 German 图1 SVM和CS-SVM在测试集上的平均误分类代价 Fig. 1 Average misclassification cost of SVM and CS-SVM in testing set 未 牢 谭 丫常 .O'。 .0 ..0 口 口 0 ..产嗽t.矿今浪'..*..‘声 。0l。a。 任勺Q帝 O 口 。 0. .队 o o. }o O n.z 口 50 100 训练 (子)样本集大小 Heart 到 一 气粉气vi 0 0 0 0 套帝本常‘ 令命.令.护气ff肠 尸 0..0-0-1.0 G I-0 0。。o.o.o.o.o.o.Q.o王 。一 尹，钾，、了 U. J}了一 0.2 ’ W 之 ;..a“之 a 丫才 ’ 卜呻- 匡 200 300 400 训练 (子)样本集大小 TP TN AC CS -TP CS -TN CS -AC German 图2 SVM和 CS-SVM在测试集上的分类精度 Fig. 2 Classification precision of SVM and CS-SVM in testing set 图 1和图2给出了基于不同尺度训练集(每个 训练集在原样本集上随机采样得到)的 CS-SVM和 SVM的测试性能，其中AV-C和 CS-AV-C分别表示 SVM和 CS-SVM在测试集上的平均误分类代价， 

298 信 息 与 控 制 35卷 TP,TN和AC分别表示基于 SVM的正例、反例分类 精度和全局精度，CS-TP, CS-TN和 CS-AC分别表示 基于CS-SVM的正例、反例分类精度和全局精度.由 图 1可见，CS-AV-C大大低于 AV-C.由图 2可见， CS-AC低于 AC，即 CS-SVM的泛化精度低于 SVM , 误差率有所提高.和SVM相比，CS-SVM在误分类代 价较高的正例样本上获得较高的分类精度，在误分 类代价较低的反例样本上获得较低的分类精度，前 者对平均误分类代价的作用大于后者，因而减小了 平均测试误分类代价. 5 结论及进一步工作(Conclusions and fur- ther works) 当样本的误分类代价不相等时，标准的基于分 类精度的算法不能直接实现数据挖掘中最小代价的 要求.通过引人概率估计和代价最小化过程，提出基 于 SVM的 CSM算法 CS-SVM.在此基础上，提出一 个通用的代价敏感分类算法 G-CSC，只要通过学习 器的输出能够估计样本属于某类的后验概率，就可 以应用 G-CSC实现 CSM. Benchmark数据试验验证了 CS-SVM的良好性 能.当每类样本的误分类代价不相等时，和 SVM相 比，尽管基于 CS-SVM的分类超平面降低了泛化精 度，有较高的误差率，但平均误分类代价大大降低. 本文也回答了上述结果产生的原因:和 SVM相比， 基于CS-SVM的分类超平面偏向于误分类代价较小 的样本簇，即偏向于反例样本，尽管误分类代价较高 的正例样本分类精度的提高牺牲了误分类代价较小 的反例样本的分类精度，但前者对平均代价的影响 大于后者，因而使平均误分类代价大大减小. 对于 CS-SVM和 G-CSC，概率估计的准确性直 接影响挖掘结果的有效性.采用有效的后验概率估 计方法，如模型集成等，是进一步的主要工作. r . . L 1 1 ， 一 一 J L es . L ， J F . es J L I . L 伟 、 ， . . J 参 考 文 献 (References Han J, Kamber M. Data Mining; Concepts and Techniques [M]，San Francisco, CA: Morgan Kaufmann, 2001. 周志华 普适机器学习〔EB/OL]. http,//www. intsci. ac. cn/research/zhouzh04.ppt, 2003. Fan W, Stolfo S, Zhang J, et al. AdaCost; misclassification cost-sensitive boosting [A]. Proceedings of the 16th Internation- al Conference on Machine Learning[C].San Francisco, CA, USA; Morgan Kaufmann, 1999. 97一105. Zadrozny B, Langford J, Abe N. Cost-sensitive learning by cost- proportionate example weighting [ A ].Proceedings of the Third IEEE International Conference on Data Mining[C].Mel- bourne, Florida Balaji Padmanabhan. University of Pennsylva- nia, 2003. 435一442. Giorgio F, Fabio R. Cost-Sensitive Learning in Support Vector Machines[EB/OL].http://www. diee. unica. it/informatica/ en/publications/papers-prag/Rel-Conference-06. pdf, 2002. Barges C. A tutorial on support vector machines from pattern recognition仁J].Data Mining and Knowledge Discovery, 1998, 2(2):121一167. Paola C, Elena C, Giorgio V. Support vector machines for can- didate modules classification[J].Neurocomputing, 2005，68 (1一4):281一288. Cover T M. Geometrical and statistical properties of systems and linear inequalities with applications in pattern recognition [j]. IEEE Transactions on Electronic Computers, 1965，14(3):326 -334. Michie D, Spiegelhalter 7, Taylor C C. Machine Learning, Neu- ral and Statistical Classification[EB/OL].http://www. nce. up. pt/liacc/ML/statlog/data. html, 1994. 作者简介 郑恩辉《1975一)，男，博士生.研究领域为人工智能，数 据挖掘，机器学习和统计学习的理论与应用. 李 平(1954-)，男，教授，博士生导师。研究领域为工 业过程模型化，智能控制，流程工业 CIMS. 宋执环(1962二 )，男，教授，博士生导师.研究领域为小 波在辫识和控制理论中的应用，预侧控制理论及应用，流程 工 业 CIMS.