54 旋转式倒立摆系统的算法研究及仿真 旋转式倒立摆系统的算法研究及仿真 江 晨 王富东 （苏州大学机电工程学院，江苏 苏州 215021） 摘 要 倒立摆主要有直线式倒立摆、旋转式倒立摆、平面倒立摆等。 选取旋转式倒立摆作为研究对象，介绍了系统的机械结构 部分，通过分析力学中的拉格朗日法建立了系统的数学模型 ，研究了两种现代控制算法在旋转式倒立摆系统中的应用 ：极 点配置法及 LQR 法，并运用 MATLAB 和 SIMULINk 工具在两种方法下进行了仿真实验，仿真结果表明：这两种算法在旋转 式倒立摆系统的控制中都是可行的，而且效果令人满意。 关键词：旋转式倒立摆，拉格朗日法，数学模型，极点配法，LQR Abstract 法，MATLAB 仿真 The inverted pendulum system mainly includes linear one,rotational one,planar one and etc．In this paper the rotational one as study object,present its mechanical structure,establish its mathematic model using the Lagrange theory in analysis dynamics,study on the application of two kinds of modern control arithmetic in rotational inverted pendulum system:Pole Configuration Method ＆ LQR Method．Finally,by using MATLAB and SIMULINK,emulational experiments are put up aimed at the two methods,the result of which indicate that:the control of the two methods in inverted pendulum system are doable and their effects turn up trumps． Keywords:rotational inverted pendulum,LAGRANGE method,mathematical model,pole configuration method,LQR method, MATLAB simulation 性 法 、 本文以一级旋转式倒立摆为例 能控性及能观性 探讨了倒立摆系统的稳定 采用极点配置法和线性二次型最优控制算 以 及 本文还对现代控 对 倒 立 摆 系 统 进 行 控 制 研 究 分别对两种方法下进行了仿真分析 MATLAB 并 通 过 ， ， ， （LQR） Simulink 制算法在倒立摆控制中存在的局限性问题进行了说明 1 一级旋转式倒立摆系统结构及其模型 1．1 。 。 所示 主 要 包 括 旋 臂 1 ， 摆 、 ， 。 等驱动 杆 、 部 分 构 系统机械结构 旋转式倒立摆的机械结构如图 直流电机以及角位移传感器 其 中 直 流 电 机 为 执 行 机 可由专门的电机驱动芯片如 由两 L298、LMD18200 个 角 位 移 传 感 器 测 量 得 到 旋 臂 作为系统 和摆杆的角位移信号 的输入量送入到控制器中 根据 一 定 的 算 法 计 算 得 到 控 制 律 并 转 化 为 电 压 信 号 提 供 给 驱 动 芯 片 从 而 来 驱 动 直 流 电 机 转 动 最终 带动旋臂在水平面内旋转 实现控制摆杆运动的效果 ， ， ， 。 ， ， 。 。 1．2 目前 系统数学模型 建立准确的数学模型是控 制系统设计的基础 人们 对倒立摆系统建模一般采用两 牛顿力学分析方法和 种方法 欧拉 本 文 中 为了简化建模过程将采用第二 种方法 ： 拉 格 朗 日 方 法 即分析力学中的 － 。 ， La- ， 方程来推导系统模型 grange 首 先 建 立 如 图 。 所 示 坐 2 标系 。 1） 对于距 计算系统总动能 点 处 、 l2 B 长为 ： dl 对 于 摆 杆 的一小段 旋 臂 和 摆 杆 的 连 接 点 为 其坐标为 ， ， ： x＝L1 *cosθ1 ＋l2 *sinθ2 *sinθ1 ** y＝L1 *sinθ1 －l2 *sinθ2 *cosθ1 ** * z＝l2 *cosθ2 这一小段的动能为 2 2 2 *dl*（x觶 ＋y觶 ＋z觶 ） B。 （1） （2） 故摆杆的总动能为 ：T2 ＝ L2 0乙 1 2 2 2 2 dl（x觶 ＋y觶 ＋z觶 ） × m2 L2 ＝ m2 2L2 L2 2 0乙 （L1 2 θ觶 1 ＋l 2 2 θ觶 2 2 ＋l 2 2 2 sin 2 θ2 θ觶 1 －2L1 l2 cosθ2 θ觶 1 θ觶 2 ）dl 2 2 2 L 1 ＋ 1 6 ＝（ 1 2 同 理 可 以 推 导 出 旋 臂 的 动 能 θ2 ）m2 θ觶 1 － 1 2 2 sin L m2 L1 L2 cosθ2 θ觶 1 θ觶 2 （3） 以 及 旋 臂 和 摆 杆 连 接 处 电 m2 L 2 ＋ 1 6 2 2 2 θ觶 2 T1 于是系统的总动能为 位器的动能 T3。 2） 势能面 计算系统总势能 则系统的总势能为 ： 以摆杆自然下垂时 质 心 所 在 平 面 为 零 ：T＝T1＋T2＋T3。 ：dT＝ 1 2 * m2 L2 0乙 dT＝ L2 ： ， m2 （1＋cosθ2 ）gL2 ＋ 1 V＝ 1 2 2 由拉格朗日方程推导系统模型 m1 gL2 ＋ 1 2 ： 3） 由以上分析 拉格朗日算子 ， H＝T－V＝ 1 6 2 m1 L1 2 1 θ觶 m3 gL2 （4） 图 1 系统结构图 2 L1 ＋ 1 6 ＋（ 1 2 － 1 m1 gL2 － 1 2 2 2 2 L 2 sin 2 θ2 )m2 θ觶 1 － 1 2 m2 L1 L2 cosθ2 θ觶 1 θ觶 2 ＋ 1 6 m2 L 2 2 θ觶 2 2 ＋ 1 2 2 m3 L1 2 1 θ觶 则由拉格朗日方程 d dt m2 （1＋cosθ2 ）gL2 － 1 2 （ 鄣H 鄣q觶 1 － 1 2 2 （m1 ＋m2 ＋m3 ）L i m3 gL2 ）－ 鄣H 鄣qi m2 L1 L2 m2 L1 L2 m2 L 2 2 1 3 ＝fi ，q＝｛θ1 ，θ2 ｝ （i＝1，2） （5） 有 ： 1 22＋ 2 0 2 θ¨ 2 2 θ¨ 2 2 Km Kc ＋c1 0 2 C2 （ 1 2 3 2 2 － 1 2 2 图 2 参考坐标系 

工业控制计算机 《 》2010 年第 卷第 期 5 23 55 Km 0 U m2 gL2 2 1 θ觶 θ觶 0 0 0 － 1 2 ＋ ＋C 记为 ：G θ¨ 1 θ¨ 2 θ2 θ1 ＝ ＋M θ2 θ觶 1 θ觶 2 θ1 ＝KU 令 x1 ＝θ1 ，x2 ＝θ2 ，x3 ＝θ觶 1 ，x4 ＝θ觶 2 则 x觶 1 ＝θ觶 1 ＝x3 ，x觶 2 ＝θ觶 2 ＝x4 ， （6） （7） 3 x觶 ＝ θ¨ 1 θ¨ 2 x觶 4 ＝－G －1 C 1 θ觶 －G θ觶 2 －1 M θ1 ＋G θ2 －1 KU 得出一阶旋转式倒立摆系统空间状态表达式为 ： 2．1 I2 －1 －1 M －G C x＋ O2 －1 K G U （8） －G ， ： 其 基 本 思 想 是 ) 从而使被控信息转换到合格范围内 年提出的 即以控制输出信息的合格度 1991 问题 ， 的依据 成果还不是很多 控制的研究还处于初始阶段 可拓控制的基本理论和方法 随着研究的不断深入 ， 们解决复杂控制系统中的难题提供一种有效的方法 从 信 息 转 换 的 角 度 去 处 理 控 制 作为确定输入矫正量 目前国内外对可拓 不过已经建立了 它将会为人 关联度 。 ， ， ， ， ( 其它智能控制算法 另外 4） 遗传控制算法等 法 几种控制算法相结合的控制方式 法的优越性 、 。 ， ， 如模糊控制算法 。 在倒立摆系统实际控制中 神 经 网 络 控 制 算 也常采用 这样可以充分利用各控制算 、 ， 来实现一种组合式的控制方法 。 。 本文中主要研究倒立摆系统的现代控制算法 系统能控性与能观性 根据系统模型 和 利用 。 （10） （11）， MATLAB ：0，7．8357，－9．8468，－2．6048， 的 函数求出 由于有非 负 的 特 eig 系统的特征值 征值 故系统不稳定 ， 由 。 中的 统能控性矩阵的秩为 MATLAB ctrb 和 满秩 ， 4， 函 数 函数 rank 所以系统完全能控 ctrb(rank(A,B)) 。 得出系 得 出 系 统 能 观 性 矩 3 2 1 O2 0 0 0 ＝ 0 00 0 0 x觶 0 x觶 0 0 x觶 00 x觶 0 1 0 0 0 0 0 0 1 0 0 00 0 0 1 0 0 0 0 0 4 x觶＝ y＝ 0 0 x 00 01 ， 。 其中 －1 ， －G C＝ 12（Km Ke ＋C1 ） 0 － 2 0 L 1 （4m1 ＋3m2 ＋12m3 ） 00 － 0 18（Km Ke ＋C1 ） L1 L2 （4m1 ＋3m2 ＋12m3 ） － － 18C2 L1 L2 （4m1 ＋3m2 ＋12m3 ） 12（m1 ＋3m2 ＋3m3 ）C2 2 m2 L 2 （4m1 ＋3m2 ＋12m3 ） 0 0 00 0 －1 －G M＝ 0 0 00 0 0 9m2 g L1 （4m1 ＋3m2 ＋12m3 ） 6（m1 ＋3m2 ＋3m3 ）g L2 （4m1 ＋3m2 ＋12m3 ） 12Km 0 00 ，G 0 －1 K＝ 0 L21（4m1 ＋3m2 ＋12m3 ） 00 0 L1 L2 （4m1 ＋3m2 ＋12m3 ） 0 00 0 摆 杆 和 角 位 移 传 感 器 质 量 18Km 其中 分别为旋臂和摆杆长度 ，m1、m2、m3 分别 为 旋 臂 、 ， 分别为电机力 矩 系 数 和 反 分 别 为 旋 臂 绕 电 机 转 轴 转 动 的 阻 尼 系 数 和 摆 ，Km、Ke L1、L2 电 势 系 数 杆绕轴转动的阻尼系数 ，C1、C2 。 将参数代入公式 和 （9）， 得到系统的数学模型 ： （8） x觶＝Ax＋BU＝ 1 0 0 0 0 0 0 0 00 0 15．2476 －3．4727 －0．2325 0 0 74．9826 －3．8965 －1．143 0 0 x＋ 00 02 0 1 y＝Cx＝ 0 0 x 00 01 2 系统控制算法研究 1 0 0 0 0 0 0 1 0 0 00 0 0 1 0 0 0 0 0 目前 ， 。 ， 但是由于 1）PID 行力学分析 制 的经验不断尝试设定 设计方案 PID 。 ， 。 国内外对于倒立摆系统的控制方法可以总结如下 控制 通常的做法是通过对倒立摆系统物理模型进 控制器实现稳定控 根据设计者 因此往往不能从推理上给出令人满意的 参数的选择通常采用尝试法进行 设计出 建立其动力学模型 PID ： ， ， ， 现代控制算法 2） 。 建立其动力学模型 现代控制算法是通过分析倒立摆数学模 然后利用状态空间理论推导出状态方程 利用现代控制理论可以设计一个基于状态反馈的 或基于线性二次型最优的控制器 型 和输出方程 控制器对系统进行极点配置 使得闭环系统在零点附近保持平稳运动 。 ， ， ， 。 可拓控制算法 。 3） 可拓控制最早是由我国的王行愚教授于 obsv rank rank(obsv(A,C)) 阵的秩为 所以系统又完全能观 由 和 满秩 4， ， 。 现代控制算法及系统仿真 （9） 2．2 极点配置法 2．2．1 ， 我们都知道 控制系统的稳定性和动态性能指标很大程度 我们进行控制系 ， 通过选择适当的状 这就是极 上取决于其闭环系统的零极点分布情况 统设计时 ， 态反馈矩阵 点配置方法 使闭环系统的极点配置在所期望的位置 可以根据对系统性能指标的要求 因此 ， ， ， ， 极点配置法是控制系统时域设计理论中最早发展起来的一 系统通过状态反馈可以任意配置闭环极点的充要 种设计思想 条件是系统必须完全能控 ， 。 解 ： 态为 系 统 完 全 能 控 时 选 取 闭 环 极 点 为 ， （30,10,0,0）， 具体程序如下 通过 ： 极 点 配 置 问 题 可 以 通 过 MATLAB 来 求 取 初 始 状 [－3．3＋0．8i －3．3－0．8i －6 －12]， 绘出系统的零输入响应图 MATLAB 。 0 0 0 0 00 4．8895 0 5．486 0 0 U （10） 00 02 ＞＞ p＝[－3．3＋0．8i －3．3－0．8i －6 －12]; ＞＞ K＝place(A,B,p); ＞＞ Ac＝A－B觹K; ＞＞ Gc＝ss(Ac,B,C,0); ＞＞ t＝0:0．1:10; （11） ＞＞ x0＝[30 10 0 0]; ＞＞ [y,t]＝initial(Gc,x0,t); ＞＞ plot(t,y(:,1),t,y(:,2)),grid ＞＞ xlabel(＇ ＞＞ ylabel(＇ 秒 时间 旋臂和摆杆的角度 ＇); ／ 度 ／ ＇) 图 由图 3 可见 3 ， 极点配置算法下，系统零输入响应的仿真结果 系统约在 后即进入稳定状态 所 以 极 点 配 3s ， 

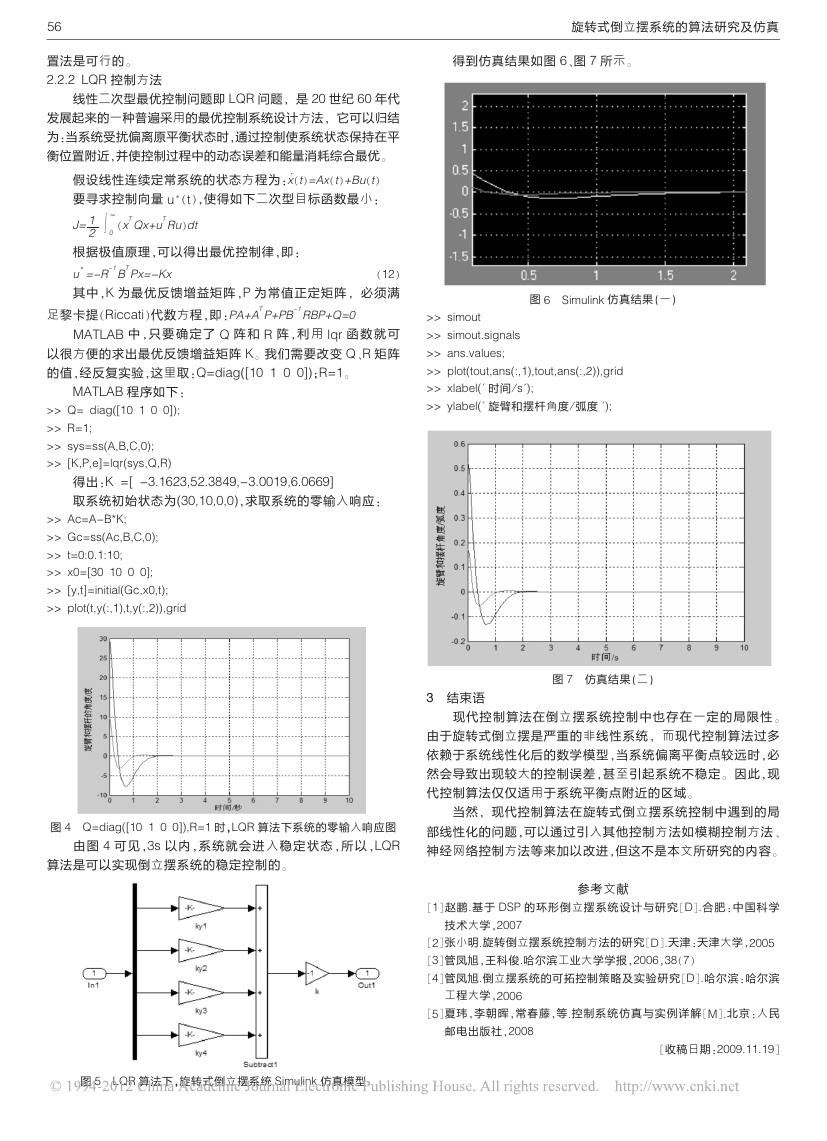
旋转式倒立摆系统的算法研究及仿真 得到仿真结果如图 图 6、 7 所示 。 图 6 Simulink 仿真结果（一） ＞＞ simout ＞＞ simout．signals ＞＞ ans．values; ＞＞ plot(tout,ans(:,1),tout,ans(:,2)),grid 时间 旋臂和摆杆角度 ／ s＇); 弧度 ／ ＇); 56 置法是可行的 2．2．2 LQR 。 控制方法 线性二次型最优控制问题即 20 发展起来的一种普遍采用的最优控制系统设计方法 为 衡位置附近 当系统受扰偏离原平衡状态时 年代 它可以归结 通过控制使系统状态保持在平 并使控制过程中的动态误差和能量消耗综合最优 问题 世纪 LQR 60 是 ： ， ， ， ， 假设线性连续定常系统的状态方程为 要寻求控制向量 使得如下二次型目标函数最小 ：x觶 （t）＝Ax（t）＋Bu（t） u*（t）， ∞ T 0乙（x J＝ 1 2 根据极值原理 Qx＋u T Ru）dt 可以得出最优控制律 即 ， ： ， －1 * ＝－R u 其中 ，K T Px＝－Kx B 为最优反馈增益矩阵 为常值正定矩阵 ，P （12） 必须满 ， 足黎卡提 （Riccati） MATLAB 中 ， 代数方程 即 ， 只 要 确 定 了 以很方便的求出最优反馈增益矩阵 的值 经反复实验 这里取 K。 ：PA＋A 阵 和 Q T －1 P＋PB 阵 RBP＋Q＝0 利 用 ， R lqr 我们需要改变 函 数 就 可 矩阵 Q、R ， ， ：Q＝diag([10 1 0 0])；R＝1。 。 ： MATLAB 程序如下 ： ＞＞ Q＝ diag([10 1 0 0]); ＞＞ R＝1; ＞＞ sys＝ss(A,B,C,0); ＞＞ [K,P,e]＝lqr(sys,Q,R) 得出 取系统初始状态为 ：K ＝[ －3．1623,52．3849,－3．0019,6．0669] (30,10,0,0)， 求取系统的零输入响应 ＞＞ Ac＝A－B觹K; ＞＞ Gc＝ss(Ac,B,C,0); ＞＞ t＝0:0．1:10; ＞＞ x0＝[30 10 0 0]; ＞＞ [y,t]＝initial(Gc,x0,t); ＞＞ plot(t,y(:,1),t,y(:,2)),grid ＞＞ xlabel(＇ ＞＞ ylabel(＇ ： 图 4 Q＝diag([10 1 0 0]),R＝1 时，LQR 算法下系统的零输入响应图 由 图 可 见 以 内 系 统 就 会 进 入 稳 定 状 态 4 ，3s ， 所 以 ， ，LQR 算法是可以实现倒立摆系统的稳定控制的 图 7 仿真结果（二） 3 结束语 现代控制算法在倒立摆系统控 制 中 也 存 在 一 定 的 局 限 性 由于旋转式倒立摆是严重的非线性系统 依赖于系统线性化后的数学模型 然会导致出现较大的控制误差 代控制算法仅仅适用于系统平衡点附近的区域 。 而现代控制算法过多 必 现 当系统偏离平衡点较远时 因此 ， 甚至引起系统不稳定 ， 。 ， ， ， ， 当然 部线性化的问题 神经网络控制方法等来加以改进 现代控制算法在旋转式倒立摆系统控制中遇到的局 可以通过引入其他控制方法如模糊控制方法 但这不是本文所研究的内容 ， 、 ， 。 。 。 ［1］ ［2］ ［3］ ［4］ ［5］ DSP ，2007 ，2006 ． ． 基于 赵鹏 技术大学 张小明 管凤旭 管凤旭 工程大学 夏玮 邮电出版社 ， ． 参考文献 的环形倒立摆系统设计与研究 合 肥 ： ［D］． 中 国 科 学 旋转倒立摆系统控制方法的研究 王科俊 ， 倒立摆系统的可拓控制策略及实验研究 哈尔滨工业大学学报 ［D］． ． ，2006，38（7） 天津 天津大学 ： ，2005 哈尔滨 哈尔滨 ： ［D］． 李朝晖 常春藤 ， 等 ． ， 控制系统仿真与实例详解 ［M］． 北京 人民 ： ，2008 ［收稿日期：2009．11．19］ 图 5 LQR 算法下，旋转式倒立摆系统 Simulink 仿真模型