Matlab教程(从新手到骨灰级玩家).pdf-资料库

b3d7be1a-6c63-4b98-87d6-c8350d9bee24.pdf-第1页.png

第1页 / 共388页

b3d7be1a-6c63-4b98-87d6-c8350d9bee24.pdf-第2页.png

第2页 / 共388页

b3d7be1a-6c63-4b98-87d6-c8350d9bee24.pdf-第3页.png

第3页 / 共388页

b3d7be1a-6c63-4b98-87d6-c8350d9bee24.pdf-第4页.png

第4页 / 共388页

b3d7be1a-6c63-4b98-87d6-c8350d9bee24.pdf-第5页.png

第5页 / 共388页

b3d7be1a-6c63-4b98-87d6-c8350d9bee24.pdf-第6页.png

第6页 / 共388页

b3d7be1a-6c63-4b98-87d6-c8350d9bee24.pdf-第7页.png

第7页 / 共388页

b3d7be1a-6c63-4b98-87d6-c8350d9bee24.pdf-第8页.png

第8页 / 共388页

下载第1章 M AT L A B是什么没有M AT L A B就没有乐趣。 Nachtigal, M. N., Reddy, S. C., Trefethen, L.N.(1990)。不对称矩阵迭代有多快？关于迭代方法的Copper Mountain会议论文集， Copper Mountain CO, 1-5,1990年4月。 1.1 MAT L A B能做什么 M AT L A B是一个可视化的计算程序，被广泛地使用于从个人计算机到超级计算机范围内的各种计算机上。 M AT L A B包括命令控制、可编程，有上百个预先定义好的命令和函数。这些函数能通过用户自定义函数进一步扩展。 M AT L A B有许多强有力的命令。例如， M AT L A B能够用一个单一的命令求解线性系统，能完成大量的高级矩阵处理。 M AT L A B有强有力的二维、三维图形工具。 M AT L A B能与其他程序一起使用。例如， M AT L A B的图形功能，可以在一个 F O RT R A N 程序中完成可视化计算。 2 5个不同的M AT L A B工具箱可应用于特殊的应用领域。 M AT L A B在以下的领域里解决各种问题是一个十分有效的工具： • 工业研究与开发。 • 数学教学，特别是线性代数。所有基本概念都能涉及。 • 在数值分析和科学计算方面的教学与研究。能够详细地研究和比较各种算法。 • 在诸如电子学、控制理论和物理学等工程和科学学科方面的教学与研究。 • 在诸如经济学、化学和生物学等有计算问题的所有其他领域中的教学与研究。 • 在M AT L A B中创建的组是矩阵， M AT L A B的名字取自矩阵实验室 ( M ATrix LABoratory)。 1.2 MAT L A B实例本节中的实例恰当而简洁地展示了 M AT L A B能做什么。在一些实例中给出了完整的 M AT L A B命令；而在另一些实例中，为简化仅给出部分命令。在本书中出现的 M AT L A B 代码用的是一种特殊的字体以区别于书中别的文字。 M AT L A B的输出是斜体字，即：我们输给 M AT L A B的命令是正体； M AT L A B给出的输出答案是斜体。百分符号％在 M AT L A B中用做注释符号，在本书中全部都是这样使用。采用的其他表示方法是：数量和预定义函数用斜体字，矩阵、向量和用户自定义函数用黑体字。矩阵用大写

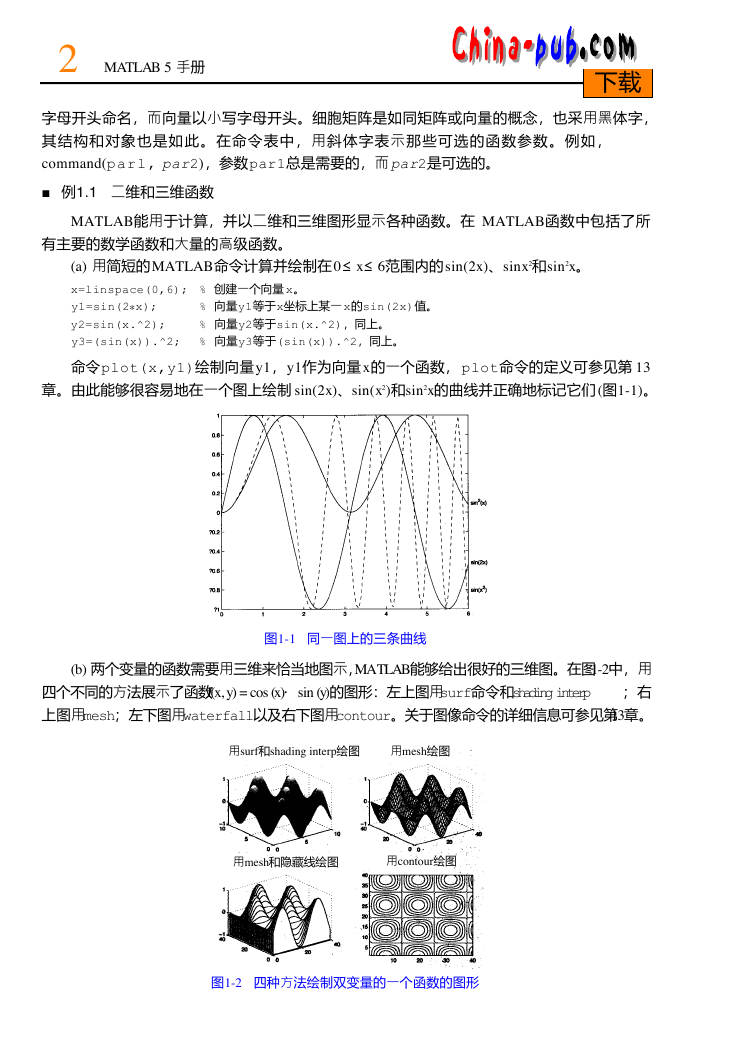
2 M ATLAB 5 手册下载字母开头命名，而向量以小写字母开头。细胞矩阵是如同矩阵或向量的概念，也采用黑体字，其结构和对象也是如此。在命令表中，用斜体字表示那些可选的函数参数。例如， c o m m a n d (parl, p a r2)，参数p a r 1总是需要的，而 p a r2是可选的。 ■ 例1.1 二维和三维函数 M AT L A B能用于计算，并以二维和三维图形显示各种函数。在 M AT L A B函数中包括了所有主要的数学函数和大量的高级函数。 (a) 用简短的M AT L A B命令计算并绘制在 0≤x≤6范围内的s i n ( 2x)、s i nx2和s i n2x。 x = l i n s p a c e ( 0 , 6 ) ; % 创建一个向量 x。 y 1 = s i n ( 2*x ) ; y 2 = s i n ( x . ^ 2 ) ; y 3 = ( s i n ( x ) ) . ^ 2 ; % 向量y 1等于x坐标上某一 x的s i n ( 2 x )值。 % 向量y 2等于s i n ( x . ^ 2 )，同上。 % 向量y 3等于( s i n ( x ) ) . ^ 2，同上。命令p l o t ( x , y 1 )绘制向量y 1，y 1作为向量x的一个函数， p l o t命令的定义可参见第 1 3 章。由此能够很容易地在一个图上绘制 s i n ( 2x)、s i n (x2)和s i n2x的曲线并正确地标记它们 (图1 - 1 )。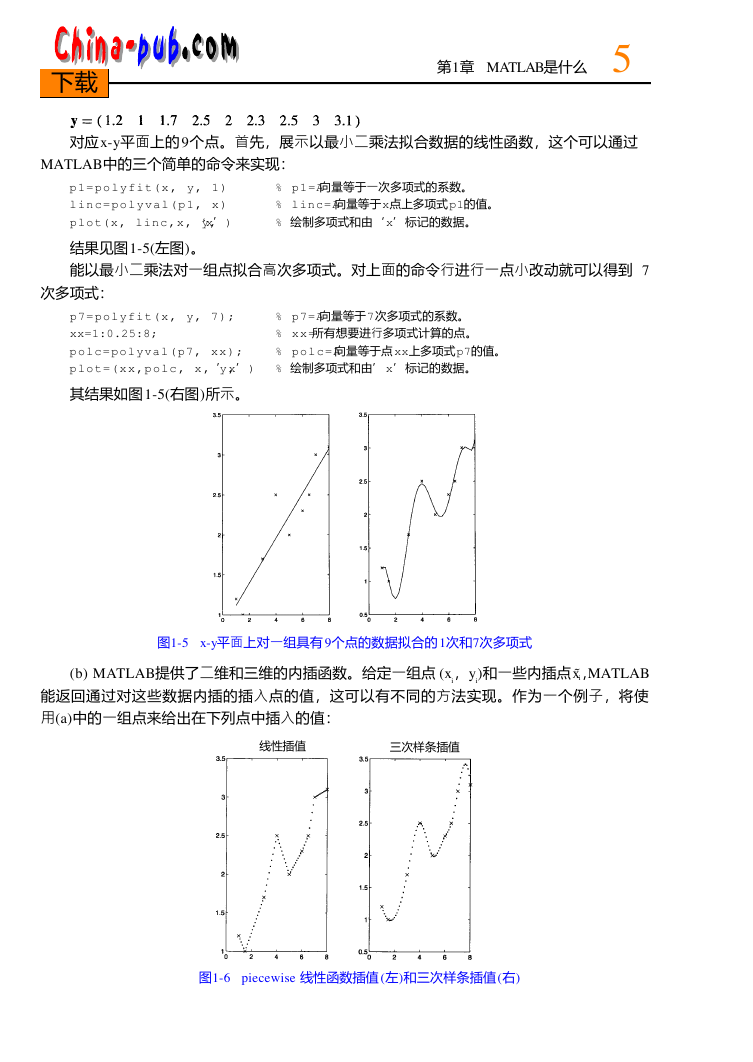图1-1 同一图上的三条曲线 (b) 两个变量的函数需要用三维来恰当地图示，M AT L A B能够给出很好的三维图。在图1 - 2中，用四个不同的方法展示了函数f(x, y) = cos (x)·sin (y)的图形：左上图用s u r f命令和shading interp ；右上图用m e s h；左下图用w a t e r f a l l以及右下图用c o n t o u r。关于图像命令的详细信息可参见第1 3章。用surf和shading interp绘图用mesh绘图用mesh和隐藏线绘图用contour绘图图1-2 四种方法绘制双变量的一个函数的图形

第1章 M AT L A B是什么 3 下载 (c) MAT L A B也能绘制一条参数曲线，例如： x-y平面图如图 1 - 3所示。图1-3 一个参数曲线图 ■ ■ 例1.2 函数分析 M AT L A B命令f z e r o和f m i n可以用于寻找一个函数的零点和最小值。函数可以用名叫 f u n c的用户自定义函数 (见2 . 9节)表示，并存入一个名叫 xex 2 - e x 2 - sin x3 f u n c . m的M文件中。这个文件由下列行组成：如果这个M文件被存放在当前的工作目录中，或在一个称为 m a t l a b的子目录中，函数f u n c 就可以像预定义的M AT L A B函数一样调用。例如，调用 x i s z e r o = f u n c ( 0 )，给出的答案是： x i s z e r o = －1 用这样定义的函数， M AT L A B提供了一个命令来寻找方程 x ex2－ex2－s i nx3= 0的零点。命令 x s o l v = f z e r o (‘f u n c’, 3) 给出： xsolv = 1 . 2 1 9 4 在本例中，命令中的第 2个自变量用的是3，是开始计算的一个初始近似值。如果在－1≤x≤1 . 5区间内绘制这个函数，则正确答案如图 1 - 4所示。图1-4 在－1≤x≤1 . 5区间内绘制函数xex2－ex2－sinx3的图形

4 M ATLAB 5 手册下载当x在0 . 5和1之间时，这个函数看起来有一个极小值，为正确找出这个极小值，用命令 m p o i n t = f m i n (‘f u n c’, 0 . 5 , 1 )，其结果为： mpoint = 0 . 8 9 5 4 用于检查M AT L A B中用户自定义函数的命令可参见第 1 0章和第11章。 ■ ■ 例1.3 线性系统与特征值 (a) MAT L A B可以用一个简单的命令行求解线性系统，系数矩阵 A和右侧b定义如下：这对应于线性系统 A x = b，如下所示：这可由如下命令求解： x = A \ b 其结果为： (b) 还有许多矩阵控制命令。例如，例 ( a )中矩阵A的特征值很容易地可以由下列命令得到：其给出：矩阵E i g e n Ve c t o r s的列是A的特征向量，E i g e n Va l u e s中对角线元素是特征值。由于矩阵 A 是对称的，因此，所有的特征值都是实数，三个特征向量是相互正交的。 ■ M AT L A B中的基本概念是矩阵。基本的矩阵命令在第 3章描述，更多的命令将在第 4、7、 8、9章中描述。 ■ 例1.4 曲线拟合与插值 (a) 如果有两个向量x和y表示的x-y平面上的一组点，那么，可以对它们进行插值点或者拟合一条曲线。令

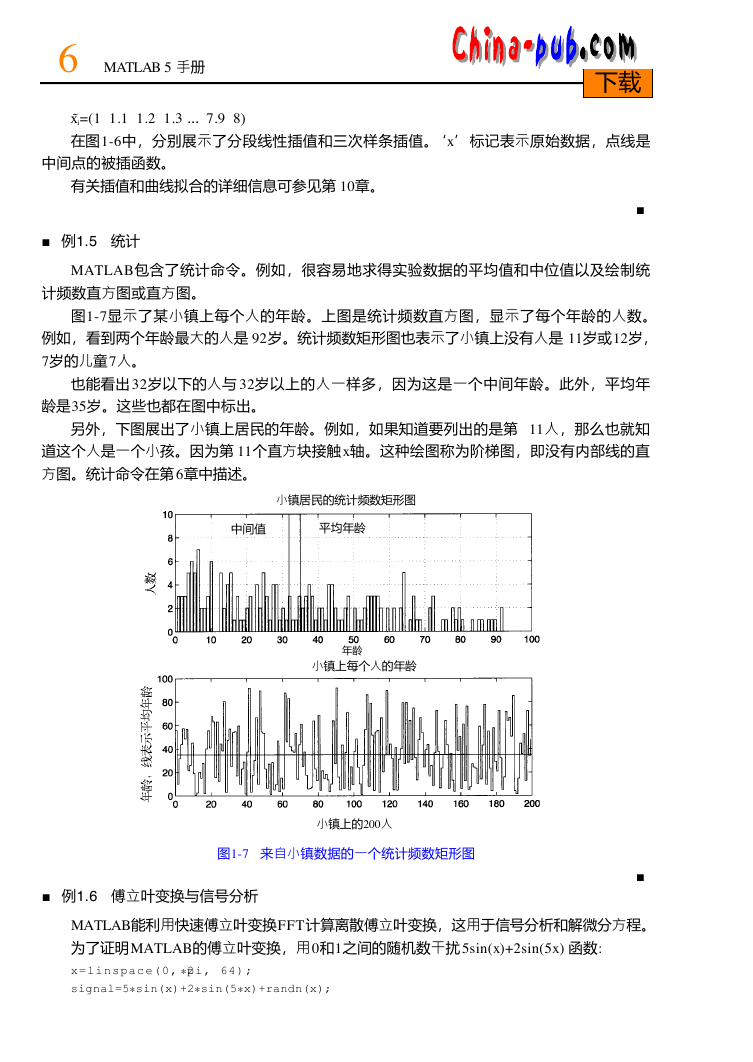
下载第1章 M AT L A B是什么 5 对应x-y平面上的 9个点。首先，展示以最小二乘法拟合数据的线性函数，这个可以通过 M AT L A B中的三个简单的命令来实现： p 1 = p o l y f i t ( x , y , 1 ) l i n c = p o l y v a l ( p 1 , x ) p l o t ( x , l i n c , x , y ,‘x’) % p1=A向量等于一次多项式的系数。 % linc=A向量等于x点上多项式 p 1的值。 % 绘制多项式和由‘ x’标记的数据。结果见图1 - 5 (左图)。能以最小二乘法对一组点拟合高次多项式。对上面的命令行进行一点小改动就可以得到 7 次多项式： p 7 = p o l y f i t ( x , y , 7 ) ; x x = 1 : 0 . 2 5 : 8 ; p o l c = p o l y v a l ( p 7 , x x ) ; p l o t = ( x x , p o l c , x , y ,’x’) % 绘制多项式和由’ x’标记的数据。 % p7=A向量等于7次多项式的系数。 % x x =所有想要进行多项式计算的点。 % p o l c = A向量等于点 x x上多项式p 7的值。其结果如图 1 - 5 (右图)所示。图1-5 x-y平面上对一组具有 9个点的数据拟合的 1次和7次多项式 (b) MAT L A B提供了二维和三维的内插函数。给定一组点 (xi，yi)和一些内插点x˜i ,M AT L A B 能返回通过对这些数据内插的插入点的值，这可以有不同的方法实现。作为一个例子，将使用( a )中的一组点来给出在下列点中插入的值：线性插值三次样条插值图1-6 piecewise 线性函数插值 (左)和三次样条插值(右)

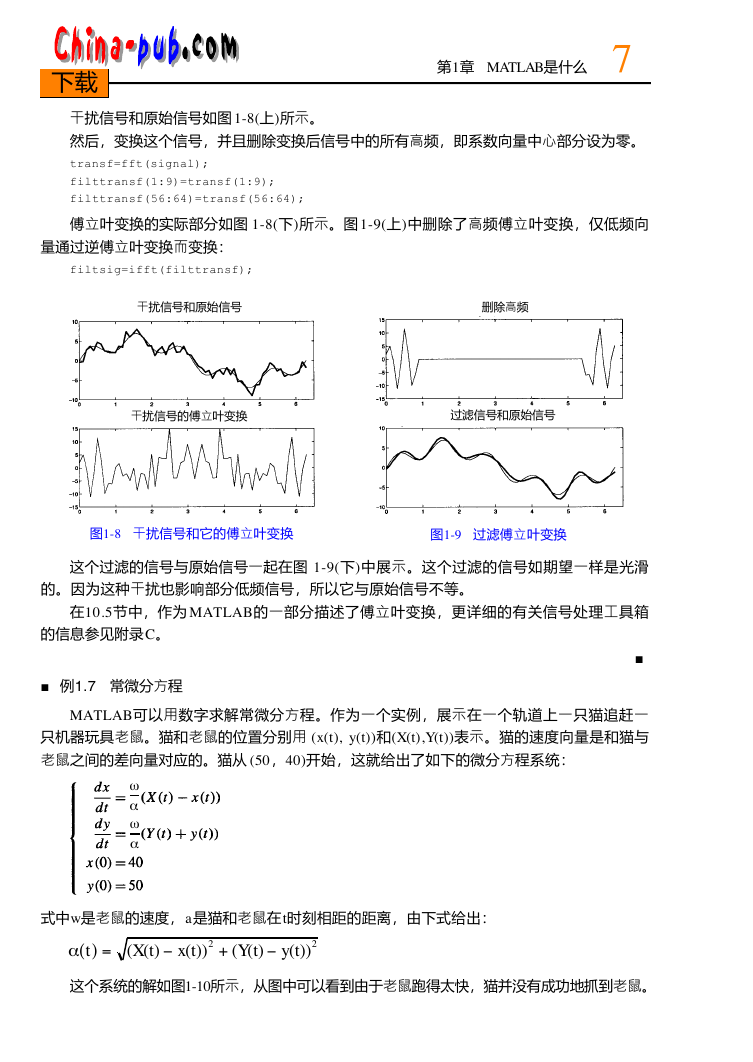
6 M ATLAB 5 手册下载 x ˜i=(1 1.1 1.2 1.3 … 7.9 8) 在图1 - 6中，分别展示了分段线性插值和三次样条插值。‘x’标记表示原始数据，点线是中间点的被插函数。有关插值和曲线拟合的详细信息可参见第 1 0章。 ■ ■ 例1.5 统计 M AT L A B包含了统计命令。例如，很容易地求得实验数据的平均值和中位值以及绘制统计频数直方图或直方图。图1 - 7显示了某小镇上每个人的年龄。上图是统计频数直方图，显示了每个年龄的人数。例如，看到两个年龄最大的人是 9 2岁。统计频数矩形图也表示了小镇上没有人是 11岁或1 2岁， 7岁的儿童7人。也能看出 3 2岁以下的人与 3 2岁以上的人一样多，因为这是一个中间年龄。此外，平均年龄是3 5岁。这些也都在图中标出。另外，下图展出了小镇上居民的年龄。例如，如果知道要列出的是第 11人，那么也就知道这个人是一个小孩。因为第 11个直方块接触 x轴。这种绘图称为阶梯图，即没有内部线的直方图。统计命令在第 6章中描述。小镇居民的统计频数矩形图中间值平均年龄年龄小镇上每个人的年龄小镇上的200人图1-7 来自小镇数据的一个统计频数矩形图 ■ 例1.6 傅立叶变换与信号分析 M AT L A B能利用快速傅立叶变换F F T计算离散傅立叶变换，这用于信号分析和解微分方程。为了证明M AT L A B的傅立叶变换，用 0和1之间的随机数干扰 5 s i n (x) + 2 s i n ( 5x) 函数: ■ x = l i n s p a c e ( 0 , 2*p i , 6 4 ) ; s i g n a l = 5*s i n ( x ) + 2*s i n ( 5*x ) + r a n d n ( x ) ;

下载第1章 M AT L A B是什么 7 干扰信号和原始信号如图 1 - 8 (上)所示。然后，变换这个信号，并且删除变换后信号中的所有高频，即系数向量中心部分设为零。 t r a n s f = f f t ( s i g n a l ) ; f i l t t r a n s f ( 1 : 9 ) = t r a n s f ( 1 : 9 ) ; f i l t t r a n s f ( 5 6 : 6 4 ) = t r a n s f ( 5 6 : 6 4 ) ; 傅立叶变换的实际部分如图 1 - 8 (下)所示。图 1 - 9 (上)中删除了高频傅立叶变换，仅低频向量通过逆傅立叶变换而变换： f i l t s i g = i f f t ( f i l t t r a n s f ) ; 干扰信号和原始信号删除高频干扰信号的傅立叶变换过滤信号和原始信号图1-8 干扰信号和它的傅立叶变换图1-9 过滤傅立叶变换这个过滤的信号与原始信号一起在图 1 - 9 (下)中展示。这个过滤的信号如期望一样是光滑的。因为这种干扰也影响部分低频信号，所以它与原始信号不等。在1 0 . 5节中，作为 M AT L A B的一部分描述了傅立叶变换，更详细的有关信号处理工具箱的信息参见附录C。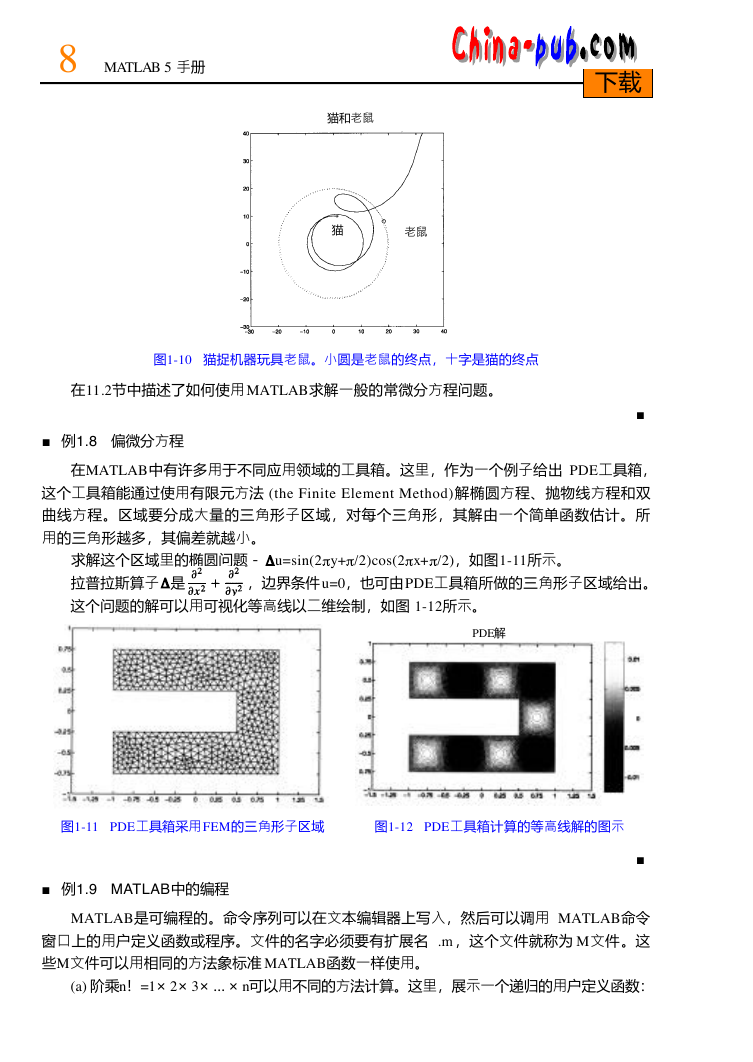 ■ 例1.7 常微分方程 ■ M AT L A B可以用数字求解常微分方程。作为一个实例，展示在一个轨道上一只猫追赶一只机器玩具老鼠。猫和老鼠的位置分别用 (x(t), y(t) )和(X(t) ,Y(t) )表示。猫的速度向量是和猫与老鼠之间的差向量对应的。猫从 ( 5 0，4 0 )开始，这就给出了如下的微分方程系统：式中w是老鼠的速度， a是猫和老鼠在t时刻相距的距离，由下式给出： a( t) = (X(t) - x(t))2 + (Y(t) - y(t))2 这个系统的解如图1 - 1 0所示，从图中可以看到由于老鼠跑得太快，猫并没有成功地抓到老鼠。 w a w a

8 M ATLAB 5 手册下载猫和老鼠猫老鼠图1-10 猫捉机器玩具老鼠。小圆是老鼠的终点，十字是猫的终点在11 . 2节中描述了如何使用 M AT L A B求解一般的常微分方程问题。 ■ ■ 例1.8 偏微分方程在M AT L A B中有许多用于不同应用领域的工具箱。这里，作为一个例子给出 P D E工具箱，这个工具箱能通过使用有限元方法 (the Finite Element Method)解椭圆方程、抛物线方程和双曲线方程。区域要分成大量的三角形子区域，对每个三角形，其解由一个简单函数估计。所用的三角形越多，其偏差就越小。求解这个区域里的椭圆问题－ u = s i n ( 2 y+ / 2 ) c o s ( 2 x+ / 2 )，如图1 - 11所示。拉普拉斯算子是这个问题的解可以用可视化等高线以二维绘制，如图 1 - 1 2所示。，边界条件 u= 0，也可由P D E工具箱所做的三角形子区域给出。 PDE解图1 - 11 PDE工具箱采用F E M的三角形子区域图1-12 PDE工具箱计算的等高线解的图示 ■ 例1.9 MAT L A B中的编程 M AT L A B是可编程的。命令序列可以在文本编辑器上写入，然后可以调用 M AT L A B命令窗口上的用户定义函数或程序。文件的名字必须要有扩展名 .m，这个文件就称为 M文件。这些M文件可以用相同的方法象标准 M AT L A B函数一样使用。 (a) 阶乘n！= 1×2×3×…×n可以用不同的方法计算。这里，展示一个递归的用户定义函数： ■

资料库

Matlab教程(从新手到骨灰级玩家).pdf

相关推荐

课程资源

热门标签

最新资料