6560
IEEE TRANSACTIONS ON AUTOMATIC CONTROL, VOL. 62, NO. 12, DECEMBER 2017
Limit-Cycle-Based Decoupled Design of Circle Formation Control
with Collision Avoidance for Anonymous Agents in a Plane
Chen Wang , Member, IEEE, and Guangming Xie , Member, IEEE
Abstract—We study the circle formation problem for a group of
anonymous mobile agents in a plane, in which the agents are re-
quired to converge onto a circle with a preset target as the center,
as well as to maintain the desired relative positions when rotating
around the target at the same speed. Each agent is modeled as a
kinematic point and can merely perceive the relative positions of
the target and its limited neighbors. In order to solve the circle for-
mation problem, a limit-cycle-based decoupled-design approach is
delivered. We divide the overall control objective into two subobjec-
tives, where the first is target circling that all agents converge onto
the circle around the target, and the second is spacing adjustment
that each agent maintains the desired distance from its neighbors.
Then, we propose to use a controller comprised of converging part
and layout part to deal with these two subobjectives, respectively.
The former part is based on a limit-cycle oscillator using only the
relative position from the target, and the latter is designed by also
perceiving the relative position from the agent’s neighbors. An im-
portant feature of the controller is that it guarantees that no col-
lision between agents ever takes place throughout the system’s
evolution. Another feature is that some of the parameters in the
proposed controller have explicit physical meanings related to the
agents’ rotating motion around the target, so that they can be set
more reasonable and easily in real applications. Numerical simula-
tions are given to show the effectiveness and performance of the
proposed circle formation controller.
Index Terms—Circle formation, collision avoidance, distributed
control, limit cycle, multi-agent system.
I.
INTRODUCTION
Multirobot systems have captured increasing attention, thanks to
their wide applications, such as exploration [2], environmental mon-
itoring [3], pursuit and evasion [4]–[6], and surveillance [7]. In such
Manuscript received November 20, 2016; revised March 1, 2017 and
May 3, 2017; accepted May 23, 2017. Date of publication June 7, 2017;
date of current version December 1, 2017. This work was supported in
part by the National Natural Science Foundation of China under Grant
61503008, Grant 91648120, Grant 51575005, and Grant 61633002, and
the China Postdoctoral Science Foundation under Grant 2015M570013
and Grant 2016T90016. This paper was presented in part at the 55th
IEEE Conference on Decision and Control, Las Vegas, USA, Dec. 12–
14, 2016[1]. Recommended by Associate Editor M. Cao. (Corresponding
author: Guangming Xie.)
C. Wang is with the State Key Laboratory of Turbulence and Com-
plex Systems, Center for Systems and Control, College of Engineer-
ing, Peking University, Beijing 100871, China (e-mail: wangchen@pku.
edu.cn).
G. Xie is with the State Key Laboratory of Turbulence and Com-
plex Systems, Center for Systems and Control, College of Engineering,
and the Institute of Ocean Research, Peking University, Beijing 100871,
China (e-mail: xiegming@pku.edu.cn).
Color versions of one or more of the figures in this paper are available
online at http://ieeexplore.ieee.org.
Digital Object Identifier 10.1109/TAC.2017.2712758
cooperative tasks, it is of benefit to keep the robots moving in a de-
sired formation with certain geometric shapes in order to success-
fully complete the tasks [8] and even to improve their performance,
such as the quality of the collected data, and the robustness of group
motion against random environmental disturbances [9]. One chal-
lenge of such a pattern formation problem for multirobot systems
arises from the fact that the robots can use only local information
to implement their distributed control strategies without centralized
coordination.
Forming circle formations is one of the most actively studied topics
within the realm of formation control, since on one hand, circle for-
mations are one of the simplest classes of formations with geometric
shapes, and on the other hand, they are natural choices of the geo-
metric shapes for a group of robots to exploit an area of interest [10].
In recent years, the circle formation problem has become challenging
since the semisynchronous model has been developed and introduced
[11]–[13]. To be more specific, the agents are assumed to be oblivious
(without memories about past actions and observations), anony-
mous (not distinguishable from one another), unable to communicate
directly, and can only interact through sensing other agents’ positions.
This model has successfully gained insight into the autonomous agents’
key characteristics, which restrict the agents’ recognition, sensing, and
communication capabilities, and these restrictions make the problem
formulation more attractive.
Based on the semisynchronous model, significant efforts have been
made on the development of distributed strategies guiding agents to
form circle formations. In particular, the focus is how to lead the agents
to distributed evenly on a circle. In the theoretical computer science
community, D´efago and Konagaya [12] have proposed algorithms to
decompose the circle formation problem into two subproblems and
solve them separately. The first is to form a circle in finite time, and
the second is to guide the robots to the configuration, where all of them
are positioned evenly on the circle. Later, these two subproblems have
been solved via a single algorithm proposed by D´efago and Souissi
[13]. Flocchini et al. [14] have investigated under what conditions the
circle formation problem is solvable by a group of identical agents with-
out a global coordinate system with the constraint that all the agents
can only move on a circle. In the systems and control community, re-
search efforts have also been made on the circle formation problem
for multiagent systems, where the dynamics of the agents are mod-
eled as single integrators [15], double integrators [16], and unicycles
[17]–[20]. Song et al. [15] have developed distributed coverage control
laws with input saturation by considering the case where agents’ mov-
ing speed is upper bounded. Marshall et al. [17] have designed a control
law under which the multiagent system’s equilibrium formations are
generalized circular pursuit patterns in the plane. Shi et al. [16] have de-
signed control protocols to achieve an equidistant circular formation for
a group of agents to enclose a team of targets. The problem of moving-
target circular formation for nonholonomic vehicles has been investi-
gated in [18] and [19]. Zheng et al. [20] have addressed the problem of
0018-9286 © 2017 IEEE. Personal use is permitted, but republication/redistribution requires IEEE permission.
See http://www.ieee.org/publications standards/publications/rights/index.html for more information.
�
IEEE TRANSACTIONS ON AUTOMATIC CONTROL, VOL. 62, NO. 12, DECEMBER 2017
6561
forming an equidistant circular formation to enclose a target for a group
of nonholonomic mobile robots with bearing-only measurements.
However, even distribution may not be the optimal configuration
when carrying out some tasks [21], only a few works [22], [23]
have considered the problem of forming arbitrary formations on a
circle. Wang et al. [22] have proposed distributed control laws to
guide the agents to form the desired circle formation. They also
discuss the corresponding sampled-data control laws and finite-time
control laws, respectively, to make the control strategies more prac-
tical. Wang et al. [23] have further considered the scenario when
the agents are under locomotion constraints. Note that their works
[21]–[23] have restricted all the agents to move in the 1-D space of a
circle.
The goal of this paper is to design distributed control laws that
can guide a group of anonymous mobile agents to form any given
circle formation in a plane. The general control objective of the prob-
lem comprises two specific subobjectives. The first is target circling
that all agents are required to converge onto a circle with a pre-
set target as the center and to rotate around the target at the same
speed, and the second is spacing adjustment that each agent needs
to maintain the desired distance from its neighbors without the re-
quirement that all the desired distances between neighboring agents
are equal. We consider a system consisting of multiple mobile agents
modeled as kinematic points, all of which move in a plane. ]s are
oblivious, anonymous, and unable to communicate directly; they can
only sense the relative position information of the target and their
neighbors.
To realize the circle formation in a plane, a limit-cycle-based
decoupled-design approach is delivered in this paper. We propose to
use a controller comprised of a converging part and a layout part to deal
with the two subobjectives of target circling and spacing adjustment,
respectively. The key idea is to first design the two parts of the controller
separately, where the converging part makes each agent converge to a
circle around the target with a prescribed radius and rotate counter-
clockwise on it, while the layout part makes all agents autonomously
adjust their positions to maintain the desired distance from their neigh-
bors. Then, with the aid of the properties of limit-cycle oscillators, we
are able to combine the two parts into a whole controller for the group
of anonymous mobile agents in a plane to solve the circle formation
problem asymptotically. We further show that the designed control law
guarantees that no collision between agents ever takes place through-
out the whole system’s evolution, and the parameters in the control law
have explicit physical meanings related to the motion characteristics of
the agents. The main contribution of the paper is then the decoupled-
design methodology based on the properties of limit-cycle oscillators
to deal with formation problems.
Compared to our previous conference paper [1], we mainly have the
following three improvements. First, a limit-cycle-based decoupled-
design approach is clearly proposed to simultaneously realize both
subobjectives, target circling and spacing adjustment, of the circle for-
mation problem. Second, a theoretical proof is given to demonstrate
that order preservation guarantees collision avoidance in our problem
setting. Third, the explicit physical meanings of the parameters in our
proposed control law are analyzed and discussed, so that these parame-
ters can be selected more reasonable and easily according to the request
of the robots’ motion characteristics when applied to real robot systems
in the future.
The rest of this paper is organized as follows. In Section II, we
formulate the circle formation problem in a plane. Then, we design a
distributed control law in Section III and provide rigorous analysis on its
performances in Section IV. Simulation results are given in Section V.
Finally, Section VI concludes this paper.
Fig. 1. Circle formation in a plane. (a) Agents are initially located
in a plane. (b) Agents form a desired circle formation and rotate
counterclockwise around the target.
II. PROBLEM FORMULATION
We consider a group of N , N ≥ 2, agents p1 , . . . , pN that are ini-
tially positioned in a plane that includes a preset target point p0 to be
circled around [see Fig. 1(a)]. The N agents are anonymous that they
cannot distinguish one from another and can move freely in the plane.
The agents’ initial positions are NOT required to be distinguished from
each other, whereas no agent occupies the same position with the tar-
get. For ease of expression, we label the agents based on their initial
positions according to the following three rules.
1) The labels are sorted first in ascending order in a counterclockwise
manner around the target.
2) For the agents who lie on the same ray extending from the target,
their labels are sorted in ascending order by the distance to the
target point.
3) For the agents who occupy the same position, their labels are
chosen randomly.
Then, we consider the case when the agents’ neighbor relationships
are described by a ring G = (V, E), where V = {1, 2, . . . , N} and
E = {(1, 2), (2, 3), . . . , (N − 1, N ), (N, 1)}. In such a way, each
agent only has two neighbors that are immediately in front of or behind
itself. We denote the set of agent i’s two neighbors by Ni = {i−, i+},
where
and
i+ =
i− =
i + 1 when i = 1, 2, . . . , N − 1
1
when i = N
when i = 1
N
i − 1 when i = 2, 3, . . . , N.
,
.
(1)
Let pi (t) = [xi (t), yi (t)]T ∈ R2 be the position of agent i, 1 ≤ i ≤ N ,
at time t, and p0 = [x0 , y0 ]T ∈ R2 is the target’s position in the plane.
Each agent is described as a kinematic point
i = 1, 2, . . . , N
where ui (t) ∈ R2 is the control input to be designed.
˙pi (t) = ui (t),
(2)
Assume that each agent can only use the relative positions between
the target and its two neighbors under the neighbor relationship G.
Note that by sensing and using the information about its two immediate
neighbors, the agents do NOT need to know the label information. In
fact, as to be proved later in Section IV, under our control laws, the
�
6562
IEEE TRANSACTIONS ON AUTOMATIC CONTROL, VOL. 62, NO. 12, DECEMBER 2017
agents’ spatial ordering will always, except in the initial state, satisfy
the first rule we just mentioned above, that is, the N agents are always
arranged in such a way that their labels are sorted in ascending order
in a counterclockwise manner around the target, so that the neighbor
relationship G is guaranteed to be time invariant. We need to emphasize
that the time-invariant neighbor relationship is not an assumption but a
nice property of our control law.
In this paper, the Circle Formation problem in a plane is formalized
as to design local controllers for all agents by only using the relative
position between the agent and the target and the relative positions
between the agent and its two neighbors such that all the agents asymp-
totically form a circle with a desired radius to keep the target p0 as its
centroid. The circle formation is required to rotate counterclockwise
around the target, and to maintain a prescribed distribution pattern with-
out the requirement that all the desired distances between neighboring
agents are equal [see Fig. 1(b)].
To formulate the problem mathematically, the following variables
are introduced. Let
¯pi (t) = pi (t) − p0 ,
i = 1, 2, . . . , N
(3)
be the relative position between agent i and the target measured by
agent i at time t. The relative position between neighboring agents can
be derived as
ˆpi (t) = pi+ (t) − pi (t),
i = 1, 2, . . . , N
(4)
where ˆpi is the relative position between agents i and i+ . It follows that
ˆpi− denotes the relative positions between agents i−
and i. We further
introduce the variables ˆαi as the angular distance from agent i to i+ ,
which is formed by counterclockwise rotating the ray extending from
the target to agent i until reaching agent i+ . It follows that ˆαi− is the
angular distance from agent i−
to i. Let di denote the desired angular
spacing from agent i to i+ . Then, the desired distribution pattern of the
N agents is determined by the vector
d = [d1 , d2 , . . . , dN ]T .
(5)
Note that only local information of di and di− in vector d is available
to each agent i. We say a prescribed circle formation is admissible if
r > 0, di > 0 and
i= 1 di = 2π, where r is the desired radius of the
circle.
N
We emphasize that, in our problem setting, each agent can only mea-
sure the relative position information of the target and its two neighbors.
More precisely, agent i can only measure the relative positions ¯pi , ˆpi
and ˆpi−. Furthermore, it is easy to check that agent i can calculate
the angular distance ˆαi just using ¯pi and ˆpi by the definition of inner
product, since ˆαi happened to be the angle between two vectors ¯pi and
¯pi + ˆpi . Similarly, agent i can calculate the angular distance ˆαi− just
using ¯pi and ˆpi−. Thus, ˆαi and ˆαi− can also be regarded as relative
information obtained by agent i (see Fig. 2).
With the above preparation, we are ready to formulate the Circle
Formation Problem in a Plane of interest. First of all, in order to
represent mathematically the N anonymous agents’ initial states with
their labels, the following two definitions for the agents’ spatial ordering
are proposed.
Definition 1 (Counterclockwise order): The N agents are said to
be arranged in a counterclockwise order if ˆαi ∈ (0, 2π) for all
i = 1, 2, . . . , N and
Definition 2 (Almost counterclockwise order): The N agents are
said to be arranged in an almost counterclockwise order if 1) ˆαi ∈
i= 1 ˆαi = 2π; and 2) ˆαi = 0
[0, 2π) for all i = 1, 2, . . . , N and
implies ¯pi+ ≥ ¯pi, where · represents the Euclidean norm.
i= 1 ˆαi = 2π.
N
N
Fig. 2.
Locally implementable control.
Then, one can check that adopting the three rules when label these
anonymous agents based on their initial positions leads to the fact that
the N agents are initially arranged in an almost counterclockwise order.
Now, we are able to present the formal problem formulation.
Definition 3 (Circle formation problem in a plane): Given an ad-
missible circle formation characterized by r and d in a plane,
laws ui (t) = ui (¯pi , ˆpi , ˆpi− , r, di , di−),
design distributed control
i = 1, 2, . . . , N , such that under any initial condition when the N
agents are arranged in an almost counterclockwise order, the solution
to system (2) converges to some equilibrium point p∗
satisfying
i = r
¯p∗
ˆα∗ = d
i = 1, 2, . . . , N
(Target circling)
(Spacing adjustment).
(6)
(7)
Furthermore, considering the possible applications to multirobot
systems, two desired/required properties of the N -agent systems are
defined as follows.
Definition 4 (Order preservation): For the N -agent system under
consideration, we say the agents’ spatial ordering is preserved under
control laws ui (t) if the N agents initially are arranged in an almost
counterclockwise order in the plane, the solution to system (2) can
ensure the N agents remain in a counterclockwise order for all t > 0.
Definition 5 (Collision avoidance): For the N -agent system un-
der consideration, we say the agents have the property of collision
avoidance if the N agents initially are arranged in an almost coun-
terclockwise order in the plane, the solution to system (2) satisfies
pi − pj > 0 for any pair of i, j (i = j) for all t > 0.
III. LIMIT-CYCLE-BASED DECOUPLED CONTROL DESIGN
In this section, using the idea of decoupled design, we propose a
control protocol with the aid of the properties of limit-cycle oscillators
to solve the circle formation problem in a plane.
As described in Definition 3, the problem includes two objectives,
target circling and spacing adjustment, which need to be concerned.
Thus, we consider a controller consisting two parts
ui (t) = up
i (t)fi (t),
i = 1, 2, . . . , N
(8)
i (t) ∈ R2 is designed to deal with the target circling objective
where up
that each agent is required to rotate counterclockwise around the target
p0 with a desired radius r, and fi (t) ∈ R1 is supposed to mainly focus
on the objective of spacing adjustment that the agents need maintain a
prescribed distribution pattern d.
First, in order to design the part up
i (t), we are going to talk a little bit
about the limit-cycle oscillators [24]. For an oscillator having a stable
limit cycle, it has the property that all trajectories in the vicinity of
the limit cycle ultimately tend toward the limit cycle as time goes into
�
IEEE TRANSACTIONS ON AUTOMATIC CONTROL, VOL. 62, NO. 12, DECEMBER 2017
6563
infinity. We find, fortunately, that such a property may fit well with
the requirement of target circling, if we could construct a second-order
nonlinear oscillator having the desired circle, which is with the desired
radius and has the target as its centroid, as its limit cycle. Following
i (t) in our controller as a limit-cycle
this idea, we design the first part up
oscillator
Substituting (8) into the dynamic equations of the system (2), we
arrive at the resulting closed-loop dynamics of the N -agent system
˙pi (t) = λ
γli(t) −1
γli (t)
1
i = 1, 2, . . . , N
¯pi (t)fi (t),
(13)
i (t) = λ
up
¯pi (t),
i = 1, 2, . . . , N
(9)
which can be rewritten equivalently using ¯pi as
γli (t) −1
γli (t)
1
where λ > 0, γ > 0 are constant, and
li (t) = r2 − ¯pi (t)2
(10)
i (t) so that fi (t) ∈ R1 . To ensure that up
shows the differences between current relative position and the desired
i (t),
one between agent i and the target. Based on such a design of up
we assume the second part fi (t) to be a coefficient of the limit-cycle
i (t) combined
controller up
with fi (t) still works for the objective of target circling, a restriction of
fi (t) > 0 and fi (t) is bounded is enforced, which will be discussed in
i (t) ∈ R2 is only
the following section. Moreover, note that the part up
using the relative position information between agent i and the given
target.
Second, taking into account the objective of spacing adjustment,
the N agents have to coordinate with each other using not only the
relative position information of the target but also that of their neigh-
bors. Due to the form of (7), which describes the spacing adjustment,
we mainly focus on the angular distance ˆαi between pairs of neighbors
when designing the part fi (t) in our controller. Following our previous
works [22], [23], we introduce an angular control uα
i (t) as
i (t) = di−
uα
di + di−
ˆαi (t) −
di
di + di−
ˆαi−(t),
i = 1, 2, . . . , N.
(11)
Then, we choose the form of fi (t) as
fi (t) = c1 + c2
2π
i (t),
uα
i = 1, 2, . . . , N
(12)
where c1 ≥ c2 > 0 are constant. We will prove in the following section
that the designed fi (t) in (12) does satisfy the restriction of fi (t) > 0
and fi (t) is bounded.
Now, we have the complete form of the distributed controller ui (t)
with its two parts up
i (t) in (9) and fi (t) in (12).
It is worth to point out that, in our designing of the controller for
each agent i, its first part is only using the relative position information
between agent i and the target, while the relative position information
of its neighbors are only used in the second part of the controller. In
other words, the first part of the controller makes each agent indepen-
dently converge to a circle around the target and rotate on it, while the
second part is used to coordinate the N agents to form and maintain a
prescribed distribution pattern when rotating on the circle. Following
these two aspects, we provide rigorous analysis for performance of the
proposed control law in Section IV.
IV. ANALYSIS OF CONVERGENCE AND COLLISION AVOIDANCE
In the previous section, a distributed control protocol (8) with (9)
and (12) has been designed. Before analyzing the performance of the
proposed control law, we first specify the form of the N -agent system
under the control law.
˙¯pi (t) = λ
¯pi (t)fi (t),
γli(t) −1
γli (t)
1
i = 1, 2, . . . , N
(14)
where fi (t) ∈ R1 and li (t) ∈ R1 are given by (12) and (10),
respectively.
Moreover, the second objective of spacing adjustment (7) in the
circle formation problem in a plane implies that the angular distance
ˆαi between pairs of neighbors becomes the focus of attention. Thus,
we treat the variables ˆαi as additional states of the N -agent system. It
is known from the definition of the angular distance ˆαi that
i = 1, 2, . . . , N
˙ˆαi (t) = ˙αi+ (t) − ˙αi (t),
(15)
where αi (t) is denoted as the angular of the vector ¯pi (t) for agent i.
Let ρi (t) ¯pi be the radius of the vector ¯pi (t) for agent i. Then,
the system (14) can be represented in the polar coordinates
cos αi (t)
sin αi (t)
¯pi (t) = ρi (t)
by
˙ρi (t) = γλρi (r2 − ρ2
˙αi (t) = λfi (t).
i )fi (t)
(16)
(17)
Consequently, we arrive at the dynamical equation of the additional
states
˙ˆαi (t) = λ[fi+ (t) − fi (t)],
(18)
where fi (t) is given by (12). It is worth to emphasize that αi (t) here
is only used for analysis purposes and is not known to the agents.
i = 1, 2, . . . , N
Now, we have the overall closed-loop system in the polar coordinates
with states ρi (t) and ˆαi (t) described by (16) and (18). We emphasize
that the overall system is a time-invariant autonomous system.
In the following two lemmas, we first prove that order preservation
implies collision avoidance in our problem setting, and then prove the
first objective of target circling in the circle formation problem in a
plane can be achieved for the closed-loop system.
Lemma 1: For the N -agent system under consideration, it has the
property of collision avoidance if the property of order preservation is
achieved.
Proof: We prove by contradiction. Suppose that there exists a tc > 0
such that at least two agents i, j collide with each other, namely pi −
pj = 0 at tc > 0. Then, it must be true that mod (θi j (tc ), 2π) = 0,
where θi j denotes the angular distance from agent i to j (i.e., θi j
is formed by counterclockwise rotating the ray extending from the
target to agent i until reaching agent j), and mod (·) is the modular
operation. Consider separately the following two cases.
Case A: j ∈ Ni . From Definitions 1 and 4, we know that
ˆαi (tc ), ˆαi−(tc ) ∈ (0, 2π). One can easily get θi j (tc ) ∈ (0, 2π) due to
the definition of θi j and j ∈ Ni . So we have arrive at a contradiction.
loss of generality, we assume
1, . . . , i, k1 , k2 , . . . , j − 1, j, . . ..
j /∈ Ni . Without
be
of
Case B:
labels
agents
the
to
�
6564
IEEE TRANSACTIONS ON AUTOMATIC CONTROL, VOL. 62, NO. 12, DECEMBER 2017
N
i= 1 ˆαi (tc ) = 2π
From Definitions 1 and 4 again, we have
and θi k 1 (tc ), θk 1 k 2 (tc ), . . . , θj−1 , j (tc ) ∈ (0, 2π). Thus, one can
have 0 < θi k 1 (tc ) + θk 1 k 2 (tc ) + . . . + θj−1 , j (tc ) < 2π, or equiva-
lent θi j (tc ) ∈ (0, 2π). However, this contradicts the assumption that
mod (θi j (tc ), 2π) = 0.
Hence, in both of the two cases, we have encountered contradiction
and this completes the proof.
Lemma 2: For each agent i, under the control law (8), the solution
to system (16) asymptotically converges to an equilibrium point ρ∗
satisfying ρi
∗ = r if fi (t) > 0 and fi (t) is bounded for all t ≥ 0.
i
i )fi (t), we can
determine that the system has two equilibrium points, ρi = 0 and
ρi = r.
Proof: From the equation 0 = γλρi (r2 − ρ2
We first check the stability of the equilibrium point ρi = 0. A
Lyapunov function candidate may be taken as
V1 (ρi ) = ρ2
i .
One can check that V1 (ρi ) is continuously differentiable and positive
definite. The derivative of V1 (ρi ) along the trajectories of the system
is given by
˙V1 (ρi ) = 2ρi ˙ρi = 2γλ(r2 − ρ2
i )ρ2
i fi (t).
In a certain neighborhood Ω of the origin (ρi = 0), both V1 and ˙V1 are
positive definite and bounded, since γ > 0, λ > 0, fi (t) > 0 and fi (t)
is bounded for all t ≥ 0. It follows the fact that the equilibrium point
ρi = 0 is unstable.
In order to show the stability of the equilibrium point ρi = r,
consider the Lyapunov function candidate
V2 (ρi ) = (r2 − ρ2
i )2 .
i )2 ρ2
i fi (t) ≤ 0.
One can check that V2 (ρi ) is continuously differentiable, positive
definite, and radially unbounded. The derivative of V2 (ρi ) along the
trajectories of the system is given by
˙V2 (ρi ) = −4(r2 − ρ2
i )ρi ˙ρi = −4γλ(r2 − ρ2
Since fi (t) > 0 and fi (t) is bounded for all t ≥ 0, one can fur-
{ρi (t) ∈ R1| ˙V2 = 0}. From the LaSalle’s theorem (see [24, Th. 4.4]),
we know that every solution starting in {ρi (t) ∈ R1} approaches
ther check that {ρi = 0}{ρi = r} is the largest invariant set in
{ρi = 0}{ρi = r} as t → ∞.
Furthermore, since the equilibrium point ρi = 0 is unstable, ρi = r
is asymptotically stable. So under the control law (8), for each agent
i, the every solution starting in {R1 − 0} approaches the equilibrium
point {ρi = r} as t → ∞.
In view of Lemma 2, we have proven the first objective of target
circling in the problem that each agent independently converges to a
circle around the target with the desired radius r when fi (t) > 0 and
fi (t) is bounded for all i = 1, 2, . . . , N and all t ≥ 0.
We go ahead analyzing the complete circle formation problem in
a plane with both the first objective of target circling and the second
objective of forming and maintaining a desired distribution pattern for
the N -agent system. For this purpose, we have to take into account the
N agents’ neighbor relationships and mainly focus on the introduced
additional states ˆαi (t).
The dynamical equation of ˆαi (t) (18) can be further written into
˙ˆαi (t) = λ[fi+ (t) − fi (t)] = λc2
2π
i+ (t) − uα
[uα
i (t)],
i = 1, 2, . . . , N.
We summarize the system dynamics into a compact form
˙ˆα(t) = − λc2
2π
L(d)ˆα(t)
(20)
(21)
where L(d) is given by (19) shown at the bottom of the this page.
In order to analyze the closed-loop system (21), we first list some
useful matrix analysis results. For a positive integer n, we use Mn
to denote the set of all n-by-n real matrices. We say a matrix A is
nonnegative (respectively, positive), denoted by A ≥ 0 (respectively,
A > 0), if all its entries are nonnegative (respectively, positive). The
directed graph of a matrix A ∈ Mn , denoted by G(A), is the directed
graph with the vertex set {vi}, i ∈ {1, 2, . . . , n}, such that there is a
directed edge in G(A) from vj to vi if and only if ai j = 0. A directed
graph is said to be strongly connected if there is a directed path between
any pair of distinct vertices [25], [26].
Lemma 3 (see[22, Lemma 5]): It holds that:
1) L(d) is diagonalizable and λi ∈ [0, 2], i = 1, 2, . . . , N .
2) 0 is a single eigenvalue.
3) When N is even, 2 is an eigenvalue, while when N is odd, 2 is not.
Now, we prove the main result in this paper.
Theorem 1: Given an admissible circle formation characterized by
r and d in a plane, the circle formation problem in a plane is solved
with collision avoidance under the proposed control law (8) with (9)
and (12).
Proof: We first prove the second objective of spacing adjust-
ment in the problem using the similar idea as in [22, Th. 1]. Let
D = diag{d1 , d2 , . . . , dN }, and then, D−1 L(d)D = LT (d). Let δ =
D−1 ˆα, and then, we have
˙δ(t) = − λc2
2π
LT (d)δ(t).
Since LT (d) is the Laplacian matrix of G(LT (d)), which is strongly
connected, we have limt→∞ δ(t) = c1N , where c is a constant. It fol-
lows then from the definition of δ that limt→∞ ˆα(t) = cd.
Furthermore, the solution to system (21) is
ˆα(t) = e− λc 2
2 π L (d )t ˆα(0),
t ≥ 0.
Since λ, c2 > 0 and from [22, Th. 1] and Lemma 3, one can know that
2 π L (d )t is positive for all t ≥ 0. The initial condition when the N
e− λc 2
agents arranged in an almost counterclockwise order (see Definition 2)
ensures that ˆα(0) ≥ 0, ˆα(0) = 0 and
N
i= 1 ˆαi (0) = 2π. So under the
initial condition, any solution to system (21) satisfies ˆα(t) > 0 and
i= 1 ˆαi (t) = 2π for all t ≥ 0. Thus, the N agents are arranged in
N
⎡
⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣
L(d) =
d 2
d 2 + d 1
+ d N
d 1 + d N
− d 2
d 2 + d 1
0
...
0
− d N
d 1 + d N
d 3
d 3 + d 2
d 2 + d 1
− d 1
d 2 + d 1
+ d 1
− d 3
d 3 + d 2
...
0
0
d 4
d 4 + d 3
d 3 + d 2
0
− d 2
d 3 + d 2
+ d 2
...
0
0
. . .
. . .
···
...
. . .
. . .
0
0
0
...
+
− d N
d N
d N −2
d N + d N −1
d N −1 + d N −2
d N + d N −1
− d 1
d 1 + d N
0
0
...
− d N −1
d N + d N −1
+ d N −1
d N + d N −1
d 1
d 1 + d N
⎤
⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦ .
(19)
�
IEEE TRANSACTIONS ON AUTOMATIC CONTROL, VOL. 62, NO. 12, DECEMBER 2017
6565
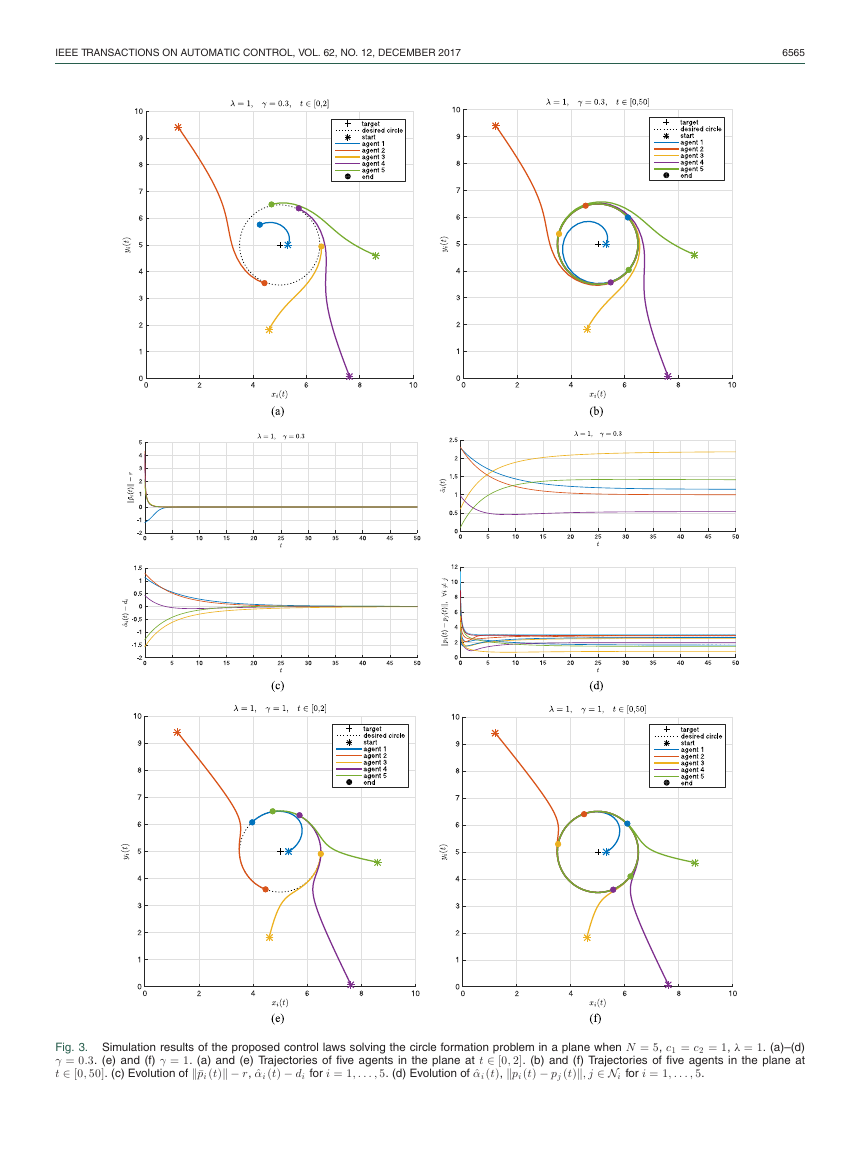
Fig. 3. Simulation results of the proposed control laws solving the circle formation problem in a plane when N = 5, c1 = c2 = 1, λ = 1. (a)–(d)
γ = 0.3. (e) and (f) γ = 1. (a) and (e) Trajectories of five agents in the plane at t ∈ [0, 2]. (b) and (f) Trajectories of five agents in the plane at
t ∈ [0, 50]. (c) Evolution of ¯pi (t) − r, ˆαi (t) − di for i = 1, . . . , 5. (d) Evolution of ˆαi (t), pi (t) − pj (t), j ∈ Ni for i = 1, . . . , 5.
�
6566
IEEE TRANSACTIONS ON AUTOMATIC CONTROL, VOL. 62, NO. 12, DECEMBER 2017
a counterclockwise order (see Definition 1) for all t > 0. Now, order
preservation has been proven to be achieved using the same techniques
as in [22, Th. 1]. Together with Lemma 1, one can have that collision
avoidance is achieved.
Then, we recall the fact we have got that limt→∞ ˆα(t) = cd, where c
i= 1 di = 2π,
i= 1 ˆαi (t) = 2π for all t and
N
N
is a constant. Noticing
it must be true that c = 1 and thus
lim
t→∞
ˆα(t) = d.
So we have proven the second objective of the problem that the
requirement of spacing adjustment is achieved with order preservation
and collision avoidance.
Now, we prove that the designed fi (t) satisfies fi (t) > 0 and fi (t)
is bounded for all i = 1, 2, . . . , N and all t ≥ 0 to ensure that the result
of Lemma 2 still works here. Since the N agents have the property of
order preservation, based on Definitions 1, 2, and 4, one can check that
i (t) ∈ (−2π, 2π) for all i = 1, 2, . . . , N and all t ≥ 0. It follows that
uα
0 ≤ c1 − c2 < fi (t) < c1 + c2 for all t ≥ 0. Further from Lemma 2,
we know that the first objective of target circling is achieved.
Summarizing the above results, we conclude that the circle formation
problem in a plane is solved with order preservation and collision
avoidance.
We want to emphasize that the parameters λ, c1 , and γ in our
proposed control law (8) have explicit physical meanings, which
play an important role in the motion characteristics of each agent i
when solving the circle formation problem in a plane. Toward this
end, we first calculate agent i’s linear velocity as vi (t) = ˙pi (t) =
i + 1 and its angular velocity relative to the tar-
get as ωi (t) = ˙αi (t) = λfi (t). Moreover, the curvature of agent i’s
trajectory at time t can be calculated as
λfi (t)¯pi (t)
γ2 l2
κi (t) =
1
2 (r2 − li ) 1
i + 1) 1
2
(γ2 l2
+
2γ2 li (r2 − li) 1
i + 1) 3
(γ2 l2
2
2
.
Then, we can also have their corresponding stable states when the N
agents solve the circle formation problem as
t→∞ vi (t) = λrc1 ,
lim
lim
t→∞ ωi (t) = λc1 ,
lim
t→∞ κi (t) =
1
r
.
In view of above equations, we can conclude that the product of the
parameters λc1 affects agent i’s linear velocity and its angular velocity
relative to the target and further determines the final stable states of
the velocity, while the parameter γ affects the curvature of agent i’s
trajectory that the larger γ implies smaller curvature. In other words,
the parameter γ determines the trajectory of each agent i, while the
product of the parameters λc1 determines how fast the agent moves on
the trajectory. Benefit from these features, the parameters λ, c1 , and γ
in our proposed control law can be selected more reasonable and easily
according to the request of the agents’ motion characteristics when
applies the control law to real robot systems in the future.
In the next section, we present simulation results that validate our
theoretical analysis in this section.
V. SIMULATIONS
In the simulations, we consider a system consisting of five agents.
The target is set at the point of (5, 5) in the plane without loss of
generality. The radius of the desired enclosing circle is r = 1.5. Both
the initial positions of the five agents and the desired distribution pat-
tern d = [1.1469, 1.0034, 2.1867, 0.5395, 1.4068]T are generated
randomly.
We first choose the parameters of the control laws (8) as c1 = c2 = 1,
λ = 1, and γ = 0.3. We run the simulations and show the results in
Fig. 3(a)–(d). Fig. 3(a) and (b) shows the trajectories of five agents in
the plane at t ∈ [0, 2] and t ∈ [0, 50], respectively. Fig. 3(c) shows the
distances between the agents to the desired circle for all the five agents,
and the differences between current angular distance and the prescribed
distances between all pairs of neighboring agents. In Fig. 3(a)–(c), the
simulation results clearly indicate that the group of agents generates
asymptotically the prescribed circle formation characterized by d and r
around the given target under the control law (8). In addition, we show
the angular distances between all pairs of neighboring agents and the
distances between any two agents of the group in Fig. 3(d). One can see
that the multiagent system under the control law (8) has the properties
of order preservation and collision avoidance.
Moreover, in order to show the physical meanings of the parameter
γ in our proposed control, we reset the parameter as γ = 1. For ease
of comparison, we use the same initial positions of the five agents and
the desired distribution pattern d and r as in the first case. We run
the simulation and show the trajectories of five agents in the plane at
t ∈ [0, 2] and t ∈ [0, 50] in Fig. 3(e) and (f), respectively. Compared
with the trajectories of the first case shown in Fig. 3(a) and (b), it is
indicated that the parameter γ determines the trajectory of each agent.
Due to a space limit, we omit the simulation results of different λ and
c1 here.
VI. CONCLUSION
In this paper, we have studied the circle formation problem for a
group of anonymous mobile agents in a plane. The problem includes
two subobjectives of target circling, for which all agents are required
to form a circle surrounding a preset target and to rotate around the tar-
get, and spacing adjustment, for which each agent has to maintain the
desired distance from its neighbors. A limit-cycle-based decoupled-
design approach has been delivered to solve the circle formation
problem. We have proposed a distributed controller comprised of the
converging part and the layout part to deal with the two subobjectives
of target circling and spacing adjustment, respectively. The former part
is based on a limit cycle using only the relative position from the target,
and the latter has been designed by also using the relative position from
the agent’s neighbors. With the aid of the properties of limit-cycle oscil-
lators, we have separately designed the two parts and finally obtained
a whole controller for the groups of anonymous agents. It has been
proven that our proposed control law can solve the circle formation
problem in a plane asymptotically with the additional guarantee that no
collision between agents ever takes place. It is worth to point out that
our controller works and guarantees collision avoidance among agents
even if some or all agents occupy the same position at the beginning.
Moreover, the parameters in the control law have explicit physical
meanings that they determine the trajectory of each agent and how fast
the agent moves on the trajectory. Thus, they can be selected more
reasonable and easily according to the request of the robots’ motion
characteristics when applied to real robot systems. We are conducting
experiments using mobile robots to implement the designed control
strategies. We are also interested in extending the work of forming
arbitrary formations on a circle in two aspects of allowing for a moving
target and modeling the agents as unicycles.
REFERENCES
[1] C. Wang and G. Xie, “Controlling anonymous mobile agents to form a
circle formation in a plane without collision,” in Proc. IEEE 55th Conf.
Decision Control, 2016, pp. 916–921.
[2] Y. Pei, M. W. Mutka, and N. Xi, “Coordinated multi-robot real-time ex-
ploration with connectivity and bandwidth awareness,” in Proc. IEEE Int.
Conf. Robot. Autom., 2010, pp. 5460–5465.
�
IEEE TRANSACTIONS ON AUTOMATIC CONTROL, VOL. 62, NO. 12, DECEMBER 2017
6567
[3] M. Dunbabin and L. Marques, “Robots for environmental monitoring:
Significant advancements and applications,” IEEE Robot. Autom. Mag.,
vol. 19, no. 1, pp. 24–39, Mar. 2012.
[4] T. H. Chung, G. A. Hollinger, and V. Isler, “Search and pursuit-evasion
in mobile robotics: A survey,” Auton. Robots, vol. 31, no. 4, pp. 299–316,
2011.
[5] W. Ding, G. Yan, and Z. Lin, “Pursuit formations with dynamic control
gains,” Int. J. Robust Nonlinear Control, vol. 22, no. 3, pp. 300–317, 2012.
[6] W. Ren, “Collective motion from consensus with cartesian coordinate
coupling,” IEEE Trans. Autom. Control, vol. 54, no. 6, pp. 1330–1335,
Jun. 2009.
[7] O. Burdakov, P. Doherty, K. Holmberg, J. Kvarnstr¨om, and P. M. Olsson,
“Relay positioning for unmanned aerial vehicle surveillance,” Int. J. Robot.
Res., vol. 29, pp. 1069–1087, 2010.
[8] K. K. Oh, M. C. Park, and H. S. Ahn, “A survey of multi-agent formation
control,” Automatica, vol. 53, pp. 424–440, 2015.
[9] F. Bullo, J. Cortes, and S. Martinez, Distributed Control of Robotic
Networks. Princeton, NJ, USA: Princeton Univ. Press, 2009.
[10] N. E. Leonard, D. A. Paley, R. E. Davis, D. M. Fratantoni, F. Lekien,
and F. Zhang, “Coordinated control of an underwater glider fleet in an
adaptive ocean sampling field experiment in Monterey Bay,” J. Field
Robot., vol. 27, pp. 718–740, 2010.
[11] I. Suzuki and M. Yamashita, “Distributed anonymous mobile robots:
Formation of geometric patterns,” SIAM J. Comput., vol. 28, no. 4,
pp. 1347–1363, 1999.
[12] X. D´efago and A. Konagaya, “Circle formation for oblivious anonymous
mobile robots with no common sense of orientation,” in Proc. 2nd ACM
Int. Workshop Principles Mobile Comput., 2002, pp. 97–104.
[13] X. D´efago and S. Souissi, “Non-uniform circle formation algorithm for
oblivious mobile robots with convergence toward uniformity,” Theor.
Comput. Sci., vol. 396, nos. 1–3, pp. 97–112, 2008.
[14] P. Flocchini, G. Prencipe, and N. Santoro, “Self-deployment of mobile
sensors on a ring,” Theor. Comput. Sci., vol. 402, no. 1, pp. 67–80, 2008.
[15] C. Song, L. Liu, and G. Feng, “Coverage control for mobile sensor net-
works with input saturation,” Unmanned Syst., vol. 4, no. 1, pp. 15–21,
2016.
[16] Y. J. Shi, R. Li, and K. L. Teo, “Cooperative enclosing control for multiple
moving targets by a group of agents,” Int. J. Control, vol. 88, no. 1,
pp. 80–89, 2015.
[17] J. A. Marshall, M. E. Broucke, and B. A. Francis, “Formations of ve-
hicles in cyclic pursuit,” IEEE Trans. Autom. Control, vol. 49, no. 11,
pp. 1963–1974, Nov. 2004.
[18] L. Brin´on-Arranz, A. Seuret, and C. Canudas-de Wit, “Cooperative
control design for time-varying formations of multi-agent systems,”
IEEE Trans. Autom. Control, vol. 59, no. 8, pp. 2283–2288, Aug.
2014.
[19] X. Yu and L. Liu, “Cooperative control for moving-target circular forma-
tion of nonholonomic vehicles,” IEEE Trans. Autom. Control, 2017, to be
published.
[20] R. Zheng, Y. Liu, and D. Sun, “Enclosing a target by nonholonomic
mobile robots with bearing-only measurements,” Automatica, vol. 53,
pp. 400–407, 2015.
[21] C. Song, L. Liu, G. Feng, and S. Xu, “Coverage control for heterogeneous
mobile sensor networks on a circle,” Automatica, vol. 63, pp. 349–358,
2016.
[22] C. Wang, G. Xie, and M. Cao, “Forming circle formations of anony-
mous mobile agents with order preservation,” IEEE Trans. Autom. Control,
vol. 58, no. 12, pp. 3248–3254, Dec. 2013.
[23] C. Wang, G. Xie, and M. Cao, “Controlling anonymous mobile agents with
unidirectional locomotion to form formations on a circle,” Automatica,
vol. 50, no. 4, pp. 1100–1108, 2014.
[24] H. K. Khalil, Nonlinear Systems, 3rd ed. Englewood Cliffs, NJ, USA:
Prentice-Hall, 2006.
[25] R. Diestel, Graph Theory. New York, NY, USA: Springer-Verlag, 1997.
[26] R. A. Horn and C. R. Johnson, Matrix Analysis. Cambridge, U.K.:
Cambridge Univ. Press, 1985.
�















 2023年江西萍乡中考道德与法治真题及答案.doc
2023年江西萍乡中考道德与法治真题及答案.doc 2012年重庆南川中考生物真题及答案.doc
2012年重庆南川中考生物真题及答案.doc 2013年江西师范大学地理学综合及文艺理论基础考研真题.doc
2013年江西师范大学地理学综合及文艺理论基础考研真题.doc 2020年四川甘孜小升初语文真题及答案I卷.doc
2020年四川甘孜小升初语文真题及答案I卷.doc 2020年注册岩土工程师专业基础考试真题及答案.doc
2020年注册岩土工程师专业基础考试真题及答案.doc 2023-2024学年福建省厦门市九年级上学期数学月考试题及答案.doc
2023-2024学年福建省厦门市九年级上学期数学月考试题及答案.doc 2021-2022学年辽宁省沈阳市大东区九年级上学期语文期末试题及答案.doc
2021-2022学年辽宁省沈阳市大东区九年级上学期语文期末试题及答案.doc 2022-2023学年北京东城区初三第一学期物理期末试卷及答案.doc
2022-2023学年北京东城区初三第一学期物理期末试卷及答案.doc 2018上半年江西教师资格初中地理学科知识与教学能力真题及答案.doc
2018上半年江西教师资格初中地理学科知识与教学能力真题及答案.doc 2012年河北国家公务员申论考试真题及答案-省级.doc
2012年河北国家公务员申论考试真题及答案-省级.doc 2020-2021学年江苏省扬州市江都区邵樊片九年级上学期数学第一次质量检测试题及答案.doc
2020-2021学年江苏省扬州市江都区邵樊片九年级上学期数学第一次质量检测试题及答案.doc 2022下半年黑龙江教师资格证中学综合素质真题及答案.doc
2022下半年黑龙江教师资格证中学综合素质真题及答案.doc