稀疏表示与压缩感知介绍.pdf

发布时间：2022-05-31 发布人：admin 分类：说明书资料大小：2.74M 资料格式：pdf 举报版权申诉

louis___zhang-12281100-16359647333305321572.pdf-第1页.png

第1页 / 共16页

louis___zhang-12281100-16359647333305321572.pdf-第2页.png

第2页 / 共16页

louis___zhang-12281100-16359647333305321572.pdf-第3页.png

第3页 / 共16页

louis___zhang-12281100-16359647333305321572.pdf-第4页.png

第4页 / 共16页

louis___zhang-12281100-16359647333305321572.pdf-第5页.png

第5页 / 共16页

louis___zhang-12281100-16359647333305321572.pdf-第6页.png

第6页 / 共16页

louis___zhang-12281100-16359647333305321572.pdf-第7页.png

第7页 / 共16页

louis___zhang-12281100-16359647333305321572.pdf-第8页.png

第8页 / 共16页

信号的稀疏表示与压缩重构

压缩感知在DOA估计中的应用

稀疏表示与压缩采样技术介绍 Introduction of Sparse Representation and Compressed Sampling Technology 汇报人：张雁峰哈尔滨工业大学（深圳） 2019 年 8 月 9 日

信号的稀疏表示与压缩重构 Outline 压缩感知在DOA估计中的应用 1 信号的稀疏表示与压缩重构 2 压缩感知在DOA估计中的应用 1 / 15

信号的稀疏表示与压缩重构 Outline 压缩感知在DOA估计中的应用 1 信号的稀疏表示与压缩重构 2 压缩感知在DOA估计中的应用 2 / 15

信号的稀疏表示与压缩重构压缩感知背景压缩感知在DOA估计中的应用 3 / 15 J. ClaerboutB. LoganD. DonohoE. CandesT. TaoR. DeVore

信号的稀疏表示与压缩重构压缩感知背景压缩感知在DOA估计中的应用 4 / 15 Traditional methodCompressive Sensing method

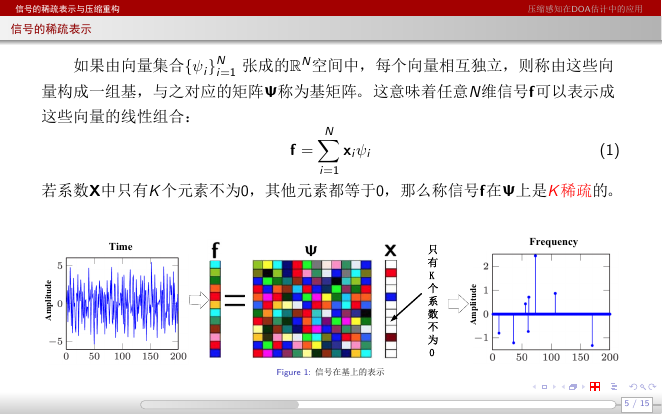
信号的稀疏表示与压缩重构信号的稀疏表示压缩感知在DOA估计中的应用如果由向量集合{ψi}N i=1 张成的RN 空间中，每个向量相互独立，则称由这些向量构成一组基，与之对应的矩阵Ψ称为基矩阵。这意味着任意N维信号f可以表示成这些向量的线性组合： f = N xi ψi (1) 若系数X中只有K 个元素不为0，其他元素都等于0，那么称信号f在Ψ上是K 稀疏的。 i=1 Figure 1: 信号在基上的表示 5 / 15 =只有K个系数不为0TimeAmplitudeFrequencyAmplitude

信号的稀疏表示与压缩重构非相关采样压缩感知在DOA估计中的应用图1所示的信号f经过采用一个大小为M × N（M N）的采样矩阵对其进行采样，这个过程可以描述如下：其中A ∈ RM×N 称为测量矩阵，y ∈ RM×1称为测量值。 y = Φf = ΦΨx = Ax (2) Figure 2: 二维空间中的p 单位球 6 / 15 =××=×measurements

信号的稀疏表示与压缩重构稀疏信号重构压缩感知在DOA估计中的应用在式(2)中，已知测量矩阵A和测量值y求解稀疏系数x的过程称为信号的重构。由于M N，式(2)是一个欠定系统，无法在多项式时间内求得精确解，因此是个NP-Hard问题。在已知稀疏度K 的前提下，式(2)可以转化为一个稀疏约束的优化问题： y − Ax2 2 x x0 ≤ K min (3) 其中x0表示向量x中非零元素的个数。若测量矩阵A满足一定程度的有限等距性质（restricted isometry property, RIP）： s.t x2 (1 − δK ) ≤ Ax2 2 2 ≤ (1 + δK ) (3)式可以以很高的概率求得精确解，其中δK 是对所有的x满足(4)式的最小常数。 (4) 7 / 15

分享到：

赞收藏

资料库

稀疏表示与压缩感知介绍.pdf

相关推荐

人工智能

热门标签

最新资料