中国科技论文在线 http://www.paper.edu.cn http://www.paper.edu.cn 基于等维灰色递补动态预测模型宏观经济指标的预测 曾希君 ,纪永强, 郑卫国 中国矿业大学计算机科学与技术学院，江苏徐州 (221116) E-mail: zengxijun530@163.com 摘摘摘摘 要：要：要：要：本文根据我国的宏观经济的两个重要指标 CPI 和 PPI 的近两年的月度数据，利用等 维灰色递补动态预测模型，使用 MATLAB 编程绘制出了 CPI 和 PPI 的递推灰色预测曲线， 然后根据曲线，对 2009 年 3 月和 4 月的 CPI 和 PPI 进行预测，预测的结果为 2009 年 3 月份 和 4 月份的 CPI 的值分别 97.82 和 95.92，即 CPI 的增长率分别为-2.18%和-4.08%。2009 年3 月份和 4 月份的 PPI 的值分别 97.82 和 95.92，即 PPI 的增长率分别为-2.18%和-4.08%。 关键词：关键词：关键词：GM(1,1)；预测；MATLAB；宏观经济指标；递推灰色 关键词： 1.1.1.1. 引言 2008 年 7 月份以来，由美国次贷危机引发的全球性金融危机已经严重影响到我国宏观经 济发展。外贸出口急剧下降，工业品出厂价格指数(PPI)和居民消费价格指数（CPI）的增幅 近几个月大幅走低，前三季度 GDP 增长率多年来首次下降到 10%以下。著名经济学家吴敬 琏预测，这场金融危机对我国实体经济的影响 2009 年可能进一步深化。对于宏观经济的走 势提前做出定量化预测，对于正确判断经济形势，制定相应的对策具有重要的意义。[1] 2222．基于等维灰色递补动态预测模型宏观经济指标的预测 2.12.12.12.1 模型的建立 灰色理论的实质是对原始随机数列采用生成信息的处理方法来弱化其随机性，使原始数 据序列转化为易于建模的新序列。灰色预测的基本原理就是确定一条通过系统的原始序列累 加生成的点群的最佳拟合曲线。 灰色预测的特点是所需的样本数较少，计算简单，因此，比传统的预测方法具有优越性 。 但是，基本的灰色预测算法也存在很多缺陷，如对于光滑离散函数建模，在数据序列随机性 较大时预测结果误差较大。 灰色系统理论指出用离散的随机数，经过生成变为随机性被显著削弱的较有规律的生成 数，这样便可以对变化过程做较长时间的描述，进而建立微分方程形式的模型。建模的实质 是建立微分方程的系数。 元素含量序列 ( )0X 有 n 个观察值， { ( ) ( ) 1 1 x 1 , ( ) ( ) 1 x 2 ,..., } ( ) ( ) x n ( ) 1 X = ( ) 0 X = 0 { ( ) ( ) x 1 , 0 ( ) ( ) x 2 ,..., 0 } ( ) ( ) x n ，通过累加生 ，其中 ( )0X n 为 个原始数据。则 GM（1，1） 成新序列 模型相应的微分方程为：[7] dX (1) dt µ a + α X (1) = µ (1) 其中： 称为发展灰数； 称为内生控制灰数。[7] αˆ 设 为待估参数向量， ˆ α ⎡ ⎤ α = ⎢ ⎥ µ ⎣ ⎦ ( YBBB 1 T n ˆ =α − ，可利用最小二乘法求解。解得：[7] ) T (2) - 1 - 

中国科技论文在线 http://www.paper.edu.cn http://www.paper.edu.cn − − 其中： ⎡ ⎢ ⎢ ⎢ ⎢ ⎢ ⋮ ⎢ ⎢ ⎢ ⎣ B = − 1 2 1 2 1 2 [ x )1( )1( + x )1( )].2( [ x )1( )2( + x )1( )]3( [ nx )1( ( )1 +− nx )] )1( ( 1 ⎤ 1 ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎦ 1 xY )0( n = [ ),2( x )0( ， 3( ),... nx )] T )0( ( (3) aˆ 将 代入微分方程式，解出白化形式的微分方程：[6] ˆ kx )1( ( + )1 = kx )1( 0 ( ) − ⎛ ⎜ ⎝ µ a ( − ⎞ kka e − ⎟ 0 ⎠ ) + µ a 将预测累加值还原为预测值：[6] )( − 将（4）代入（5）化简即得：[6] )( ˆ kxkxkx )0( = )1( )1( ( ˆ ˆ − )1 ˆ kx )( )0( = kx )1( 0 ( ) − ⎛ ⎜ ⎝ ( e − µ a ⎞ ⎟ ⎠ kka ( 0 − )1 − − e − kka ( 0 − − ))2 (4) (5) (6) 如果将所有的已知数据都作为灰色系统模型的数据输入与输出，得到的微分方程的系数 和 是固定的，以后的预测值就有这两个固定的参数值决定，不能够体现出新数据对未 a µ 来预测值的影响，而有使得过时的数据在预测中的作用没有减弱。[6] 鉴于这种情况,可先用已知数列建立的 GM(1 ,1) 模型预测一个值,然后补充一个新信息数 据到已知数列中,同时去掉最老的一个数据,使序列等维,接着再建立 GM(1 ,1) 模型,这样用预 测灰数新陈代谢,逐个滚动预测,依次递补,直到完成预测目标. 这种 GM(1 ,1) 模型的特点是: ①及时补充和利用灰信息,缩小了预测值的灰区间; ②每预测一步,对灰参数作一次修正,并随 之修正模型,使预测值在动态过程中产生; ③可用较短数列进行长期预测,但也不能无止境的 预测下去. 由于考虑到与预测期接近的数据更有效,因此该模型预测精度比全数据 GM(1 ,1) 模型有显著提高。 设原始数据序列为 x(0) = [ x(0) (1) ,x(0) (2) , ⋯,x(0)(n) ] ,对原始数据序列 x(0) 进行一次 AGO 生成 x (1) 后建立 GM(1 ,1)，得到 n + 1 时刻预测值^ x(0) ( n+ 1) ,然后去掉 x(0) (1) , 加入灰色^ x(0) ( n+ 1) ,重新构成等维动态序列:x1(0) = [ x(0) (2) , x(0) (3) , ⋯, x(0) ( n) , ^ x(0) ( n+ 1) ]，建立新的 GM(1 ,1) 模型在预测 n + 2 时, ^x(0)( n+ 2) , ⋯,如此递补,逐个预测。 由于等维灰数递补动态预测加入的信息不是实测值而是预测值,它可以淡化灰平面的灰度,但 仍然是灰色的。科学的建模过程应该是，一旦获得 n + 1 时的实际观测数据(称为新信息) ， 便对原来的 GM(1 ,1)模型进行一次改进。其方法是在序列 x(0) = [ x(0) (1) ,x(0) (2) , ⋯,x(0) (n) ]中去掉 x(0) (1) ,加入 x(0) (n + 1) ,构成新的动态序列: x1= [ x(0) (2) , x(0) (3) , ⋯, x(0)( n) , x (0) ( n+ 1) ] 。由于等维新信息模型实时引入的是新的观测值,因此真实地反映了系统状态的 变化，可有效地提高预报精度。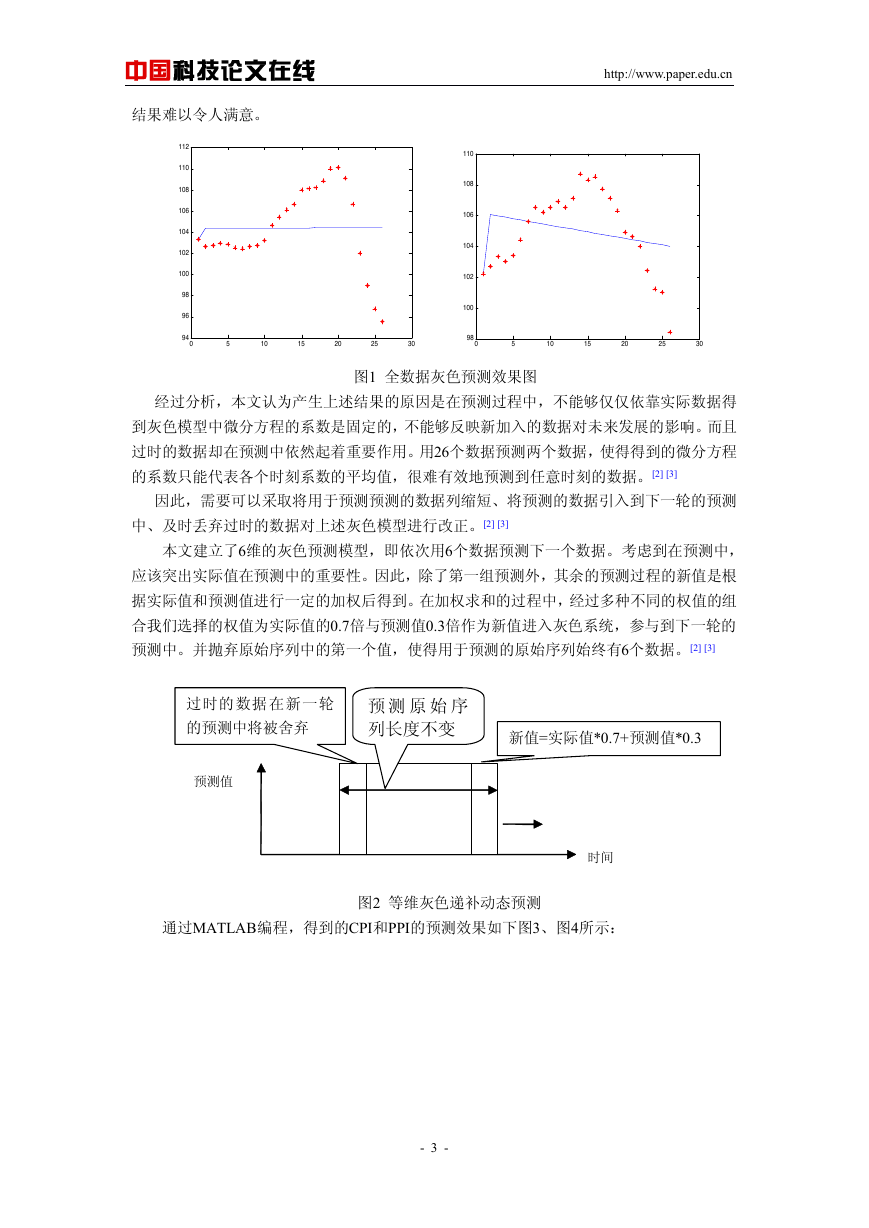[6] 2.22.22.22.2 模型的求解 首先本文采用了全数据的灰色模型GM(1,1)预测数据，预测的拟合效果如下面的图1所示， - 2 - 

中国科技论文在线 http://www.paper.edu.cn http://www.paper.edu.cn 结果难以令人满意。 GM(1,1 112 110 108 106 104 102 100 98 96 I P P GM(1,1) 110 108 106 104 102 100 I P C 94 0 5 10 15 20 25 30 98 0 5 10 15 20 25 30 图1 全数据灰色预测效果图 经过分析，本文认为产生上述结果的原因是在预测过程中，不能够仅仅依靠实际数据得 到灰色模型中微分方程的系数是固定的，不能够反映新加入的数据对未来发展的影响。而且 过时的数据却在预测中依然起着重要作用。用26个数据预测两个数据，使得得到的微分方程 的系数只能代表各个时刻系数的平均值，很难有效地预测到任意时刻的数据。[2] [3] 因此，需要可以采取将用于预测预测的数据列缩短、将预测的数据引入到下一轮的预测 中、及时丢弃过时的数据对上述灰色模型进行改正。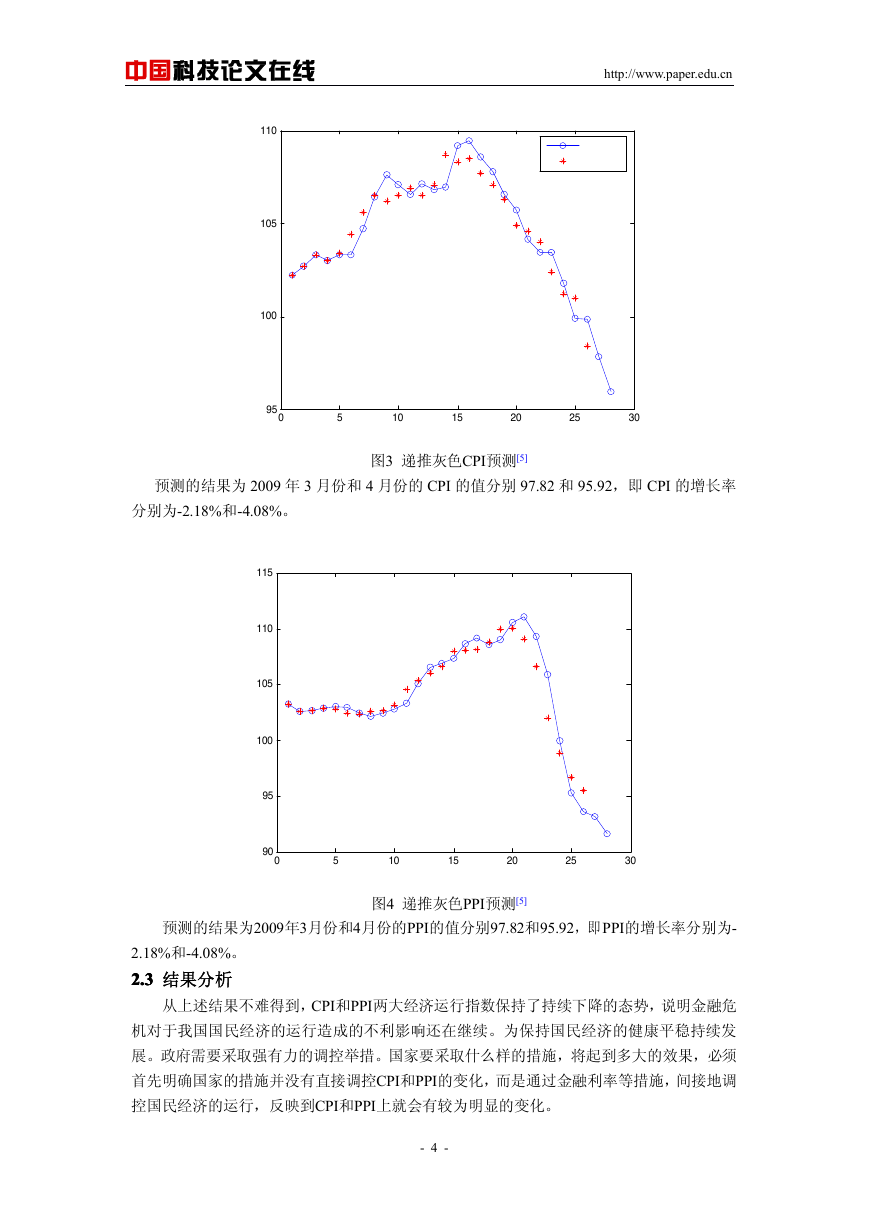[2] [3] 本文建立了6维的灰色预测模型，即依次用6个数据预测下一个数据。考虑到在预测中， 应该突出实际值在预测中的重要性。因此，除了第一组预测外，其余的预测过程的新值是根 据实际值和预测值进行一定的加权后得到。在加权求和的过程中，经过多种不同的权值的组 合我们选择的权值为实际值的0.7倍与预测值0.3倍作为新值进入灰色系统，参与到下一轮的 预测中。并抛弃原始序列中的第一个值，使得用于预测的原始序列始终有6个数据。[2] [3] 过时的数据在新一轮 的预测中将被舍弃 预 测 原 始 序 列长度不变 新值=实际值*0.7+预测值*0.3 预测值 通过MATLAB编程，得到的CPI和PPI的预测效果如下图3、图4所示： 图2 等维灰色递补动态预测 时间 - 3 - 

中国科技论文在线 http://www.paper.edu.cn http://www.paper.edu.cn GM( 1, 1) 110 105 100 I P C 95 0 5 10 15 20 25 30 图3 递推灰色CPI预测[5] 预测的结果为 2009 年 3 月份和 4 月份的 CPI 的值分别 97.82 和 95.92，即 CPI 的增长率 分别为-2.18%和-4.08%。 115 110 105 100 95 90 0 I P P PPI 5 10 15 20 25 30 图4 递推灰色PPI预测[5] 预测的结果为2009年3月份和4月份的PPI的值分别97.82和95.92，即PPI的增长率分别为- 2.18%和-4.08%。 2.2.2.2.3333 结果分析 从上述结果不难得到，CPI和PPI两大经济运行指数保持了持续下降的态势，说明金融危 机对于我国国民经济的运行造成的不利影响还在继续。为保持国民经济的健康平稳持续发 展。政府需要采取强有力的调控举措。国家要采取什么样的措施，将起到多大的效果，必须 首先明确国家的措施并没有直接调控CPI和PPI的变化，而是通过金融利率等措施，间接地调 控国民经济的运行，反映到CPI和PPI上就会有较为明显的变化。 - 4 - 

中国科技论文在线 http://www.paper.edu.cn http://www.paper.edu.cn 3.3.3.3.结论 本文运用等维灰色递补动态预测模型，利用MATLAB软件绘制出了我国宏观经济的两个 重要指标CPI和PPI在2007-2009年每个月的曲线图，由此可以预测2009年3月和4月我国CPI 和PPI的值，并且去求出了CPI和PPI的同比增幅，以及预测误差。本文的方法直观易懂，是 一种较好的处理预测问题的方法，可以推广到其它相似的预测领域，有利于解决实际问题。[4] 参考文献 [1]国家统计局，中华人民共和国国家统计局，http://219.235.129.54/cx/left_sc.jsp?bbzl=103，2009 年 3 月 13 日。 [2]杨启帆.方道元.数学建模 [M].浙江：浙江大学出版社，1999:69-70. [3]曹德欣,曹璎珞.计算方法 [M].江苏：中国矿业大学出版社，2001：104-109 [4]陆诚煜.我国私人汽车保有量的分析及预测 [D].南京：南京财经大学本科，2007. [5]张兴永. Matlab 软件与数学实验 [M].江苏：中国矿业大学大学出版社，2007：70-73. [6]龙文, 黄汉明, 赵东泉, 覃邦余,城市人口系统等维灰数递补动态模型探讨[J]安徽农业科学, 2007 ,35 (36) :11740 - 11741 [7]高传昌, 刘新阳 等维灰数递补动态模型在城市生活用水量预测中的应用[J]灌溉排水学报 2005 ,24 (6) :71 TTTThehehehe FFFForecast ndicators BBBBasedasedasedased onononon GGGGray- ndicators acro-economic orecast ofofofof MMMMacro-economic orecast ray- acro-economic IIIIndicators orecast acro-economic ndicators ray- ray- dimensional ynamic ynamic MMMModelodelodelodel dimensional DDDDynamic dimensional ynamic dimensional ZENG Xijun, JI Yongqiang, ZHENG Weiguo Department of Computer Science and Technology, China University of Mining and Technology, Xuzhou (221116) Abstract Abstract Abstract Abstract In this paper, according to China's two important macroeconomic indicators of the CPI and PPI monthly data over the past two years, the use of gray-dimensional dynamic forecasting model to fill, the use of MATLAB programming to map out the CPI and PPI Recursive gray prediction curve, then curve, in March 2009 to April's CPI and PPI to predict and forecast the results of March 2009 and in April the CPI value of 97.82 and 95.92, respectively, that is, the growth rate of CPI were -2.18% and - 4.08 %. In March 2009 and in April the value of PPI of 97.82 and 95.92, respectively, that is, the growth rates of CPI were -2.18% and -4.08%. words: GM (1,1); forecast; MATLAB; macro-economic indicators; recursive Gray KeyKeyKeyKey words: words: words: - 5 -