logo资料库

LCL滤波器的单相光伏并网控制策略.pdf

发布时间：2022-05-30 发布人：admin 分类：说明书 资料大小：1.06M 资料格式：pdf 举报 版权申诉
第1页 / 共8页
第2页 / 共8页
第3页 / 共8页
第4页 / 共8页
第5页 / 共8页
第6页 / 共8页
第7页 / 共8页
第8页 / 共8页
资料共8页，全文预览结束
    第 31 卷 第 21 期 2011 年 7 月 25 日 文章编号：0258-8013 (2011) 21-0017-08 中图分类号：TM 615 文献标志码：A 学科分类号：470⋅40 Vol.31 No.21 Jul.25, 2011 ©2011 Chin.Soc.for Elec.Eng. 中 国 电 机 工 程 学 报 Proceedings of the CSEE 17 LCL 滤波器的单相光伏并网控制策略 彭双剑，罗安，荣飞，吴敬兵，吕文坤 (湖南大学电气与信息工程学院，湖南省 长沙市 410082) Single-phase Photovoltaic Grid-connected Control Strategy With LCL Filter PENG Shuangjian, LUO An, RONG Fei, WU Jingbing, LÜ Wenkun (College of Electrical and Information Engineering, Hunan University, Changsha 410082, Hunan Province, China) ABSTRACT: Single-phase photovoltaic grid-connected generator systems adopt LCL filter which is useful to restrain high-frequency switching current into the grid. However, the LCL filter increases the system order so that the design of the system stability is difficult to be realized. At present，dual-loop control strategies which consist of dc-side voltage outer loop and grid-side current inner loop have been widely used for single-phase photovoltaic grid-connected generator systems with L or LC filters. But if the dual-loop control is directly used in the photovoltaic system with the LCL filter, the system may be unstable. This paper presented a novel grid-connected control strategy composed of voltage loop, power loop, and capacitor current loop. The voltage loop stabilized the capacitor voltage at dc-side of the grid-connected inverter; the power loop regulated the power factor of photovoltaic grid-connected generating power; both the power loop and the capacitor current loop improved the system stability and suppress resonant peak caused by the LCL filter. The system closed-loop transfer function was derived and the influence of control parameters on the system stability was analyzed with the closed-loop pole distribution. Simulation and experiment results demonstrate the feasibility of the proposed control system. KEY WORDS: closed-loop pole; grid-connected control; transfer function; single-phase photovoltaic generation; current control; power regulation; LCL filter; stability 摘要：单相光伏并网发电系统采用 LCL 滤波器有利于抑制高 频开关谐波电流进入电网，但是 LCL 滤波器增加了系统的阶 数，增大了系统稳定性的设计难度。直流侧电压外环、网侧 电流内环的双环控制策略适用于采用 L 或者 LC 滤波器的单 基 金 项 目 ： 国 家 重 点 基 础 研 究 发 展 计 划 项 目 (973 计 划 ) The National Basic Research (2009CB219706)；国家自然科学青年基金项目(50907017)。 (973 Program) (2009CB219706); Projected Supported by National Nature Science Youth Foundation (50907017). Program 相光伏并网发电系统，但不利于基于 LCL 滤波器系统的稳定 性。提出一种电压环、功率环和电容电流环的并网控制策略， 电压环稳定并网逆变器直流侧电容两端的电压，功率环调节 光伏并网发电的功率因数，功率环和电容电流环共同提高系 统的稳定性和抑制 LCL 滤波器引起的谐振尖峰。推导了系统 的闭环传递函数，分析了控制参数对系统闭环极点分布和稳 定性的影响。仿真和实验结果验证了所提控制策略的可行性。 关键词：闭环极点；并网控制；传递函数；单相光伏发电； 电流控制；功率调节；LCL 滤波器；稳定性 0 引言 太阳能的利用是缓解全球能源短缺问题的重 要途径，光伏发电就是太阳能利用研究的热点之 一。随着半导体产业技术的进步，光伏电池的效率 逐步提高，光伏发电的单位成本正在逐步下降，使 其民用化成为可能。 并网逆变器是光伏并网发电系统的核心部件， 它的主要功能是将光伏阵列转化的直流电变换成 电网同步的交流电，它的控制好坏直接关系到系统 的整体性能，因此得到了很多研究工作者的关注。 为了防止开关谐波污染电网，并网逆变器与电网之 间通常连有滤波器。适用于电压源型逆变器的滤波 器有 L 型、LC 型和 LCL 型，由于 LCL 型滤波器在 低开关频率和小电感情况下较前 2 种滤波器可以获 得更好的谐波抑制性能，而被广泛采用[1-8]，但是在 实现稳定的并网控制上要复杂得多。 采用 L 型或者 LC 型的单相光伏并网发电系统 通常采用电压外环、网侧电流内环的双环控制策 略[9-11]，但是不能确保基于 LCL 滤波器的系统稳定 控制[3,8]。因此，基于 LCL 滤波器的单相光伏并网 发电系统可以采用电压环、网侧电流环和电容电流
    18 中 国 电 机 工 程 学 报 第 31 卷 环的三环控制策略，由于电压外环的存在，网侧电 流环采用 PI 控制器可以实现有功电流的无稳态误 差调节，但是对无功电流没有调节效果，难以保证 光伏并网发电的单位功率因数。虽然文献[4]提出了 功率控制策略可以提高入网电流的幅值精度和功 率因数，但没有对控制系统的稳定性和参数设计进 行分析。本文提出了一种新型基于 LCL 滤波器的单 相光伏并网控制策略，由电压环、功率环和电容电 流环组成，电压环确保并网逆变器直流侧电压稳 定，功率环实现光伏并网电流的无静差和功率因数 控制，电容电流环可提高控制系统的动态性能和谐 振抑制能力。研究了基于 PQ 理论的单相电流检测 技术，并推导了系统的闭环传递函数，根据闭环极 点分布分析了系统的稳定性，设计了控制系统的调 节参数。最后，仿真和实验结果证明了所提控制策 略的正确性。 1 单相光伏并网发电系统 系统结构如图 1 所示，分为电气电路和控制 2 部分。光伏组件阵列正负输出端接升压斩波电路， 它的输出端通过电容器 Cdc 与逆变器的直流侧相 连，逆变器的交流侧接 LCL 输出滤波器，并与电网 连接。图 1 中，UPV 和 IPV 分别为光伏组件阵列的正 负端电压和输出电流；Udc 为并网逆变器直流侧电 容器 Cdc 两端的电压；R1 和 R2 分别表示 LCL 滤波 器电感 L1 和 L2 的内阻；iI 为并网逆变器输出电流； ic 为流过滤波电容 Cf 的电流；uc 为滤波电容 Cf 的端 电压；is 和 us 分别为光伏发电网侧电流和电网电压。 太 光伏组件阵列 阳 光 照 IPV 升压斩波电路 Cdc 逆变器 + UPV − + Udc − iI L1 LCL 滤波器 is L2 R2 R1 Cf ic uc PWM UPV IPV MPPT 控制 PWM Udc 并网控制 ic us is 图 1 系统结构 Fig. 1 System structure 电网 + us − 系统控制分为升压斩波电路的 MPPT 控制和逆 变器的并网控制。光伏组件阵列作为能源转换器 件，它的输出功率除了受环境温度和光照强度这些 外界因素决定外，其端电压 UPV 也起到决定性作用， 由它的端电压−功率曲线可知控制 UPV 就可以确定 阵列输出功率，MPPT 控制的意义就是搜索到 UPV 的参考值，保证光伏组件阵列在任何时刻输出最大 功率，提高光电转换效率。文献[12-15]对 MPPT 控 制做了很多研究工作，本文就不赘述了。下面将分 析新型单相光伏并网控制策略，为了给新型控制策 略在实现过程中提供特定的数据，本文首先研究了 单相瞬时电流的检测。 2 基于 PQ 理论的单相电流检测 不考虑谐波电压，将 us 和 is 分别延时 90°，并 构造αβ坐标系正交两相电压电流，即 ⎧ i ⎪⎪ s α ⎨ ⎪ i s β ⎪⎩ = = i s 2 = − 2 ∞ ∑ n 1 = ∞ ∑ n 1 = I s n I n s sin( n t ω θ n 0 − ) cos( n t ω θ n 0 − ) (2) 式中：Us 为 us 的有效值；ω0 为工频角速度；Isn 为 is 中所含 n 倍基波频率电流分量的有效值，n=1, 3,…,即当 n=1 时 Is1 是 is 中所含基波电流分量的有 效值；θn 为 is 中所含 n 倍基波频率电流分量的相位 偏移。 由瞬时无功功率理论[16-17]可知，有功和无功电 流 spi 、isq 的直流量 spI 和 sqI 可以由式(3)变换后通过 低通滤波器滤除交流量 spi% 、 sqi% 得到 ⎡ ⎢ ⎣ (3) i s α i s β C αβ − i % sp i % sq i sp i sq + + ⎤ ⎥ ⎦ = = pq I I ⎡ ⎢ ⎢ ⎣ sp sq ⎡ ⎢ ⎣ ⎤ ⎥ ⎦ ⎤ ⎥ ⎥ ⎦ ⎧ u ⎪ s α ⎨ u ⎪⎩ s β u = s = − = U 2 U 2 s cos t sin ω 0 t ω 0 s (1) 其中，变换矩阵 C αβ − pq ⎡ = ⎢ ⎣ sin cos − t ω 0 t ω 0 − − cos sin t ω 0 t ω 0 ⎤ ⎥ ⎦ 。
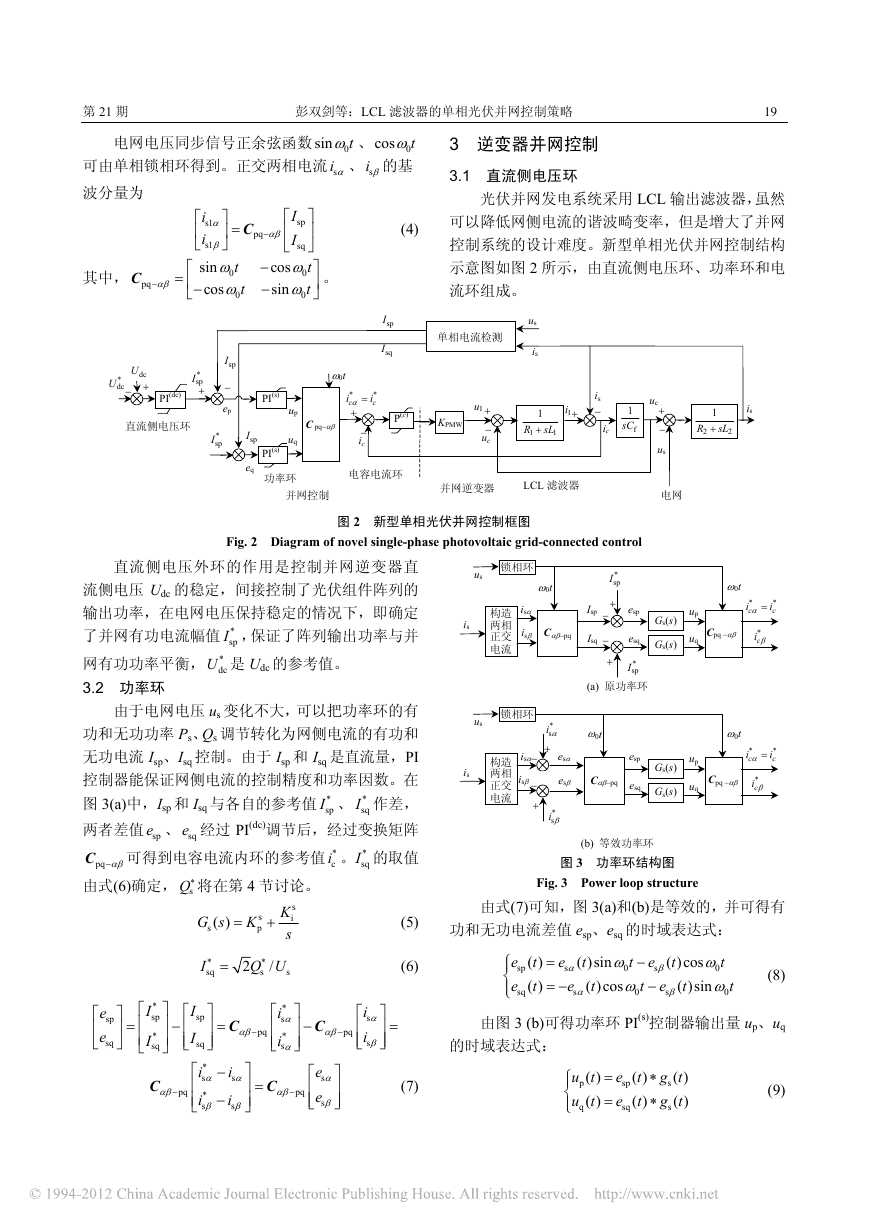
    第 21 期 彭双剑等：LCL 滤波器的单相光伏并网控制策略 19 电网电压同步信号正余弦函数 tω 0 可由单相锁相环得到。正交两相电流 si α 、 si β的基 波分量为 tω 、 cos sin 0 C α = i ⎤ ⎡ s1 ⎥ ⎢ i ⎦ ⎣ s1 β t sin ω 0 t cos − ω 0 其中， C pq αβ − ⎡ = ⎢ ⎣ pq − αβ ⎡ ⎢ ⎣ cos sin sp I ⎤ ⎥ I ⎦ sq t ω ⎤ 0 ⎥ t ω ⎦ 0 − − 。 (4) 3 逆变器并网控制 3.1 直流侧电压环 光伏并网发电系统采用 LCL 输出滤波器，虽然 可以降低网侧电流的谐波畸变率，但是增大了并网 控制系统的设计难度。新型单相光伏并网控制结构 示意图如图 2 所示，由直流侧电压环、功率环和电 流环组成。 * spI + * dcU dcU − + PI(dc) 直流侧电压环 spI − ep * spI spI eq PI(s) up uq PI(s) 功率环 spI sqI 单相电流检测 us is P(c) KPMW uI + − uc iI + 1 sL+ 1 R 1 is − ic 1 sC f uc + − us is 1 sL+ 2 R 2 ω0t * * i iα = c c + − ic C pq−αβ 并网控制 电容电流环 并网逆变器 LCL 滤波器 电网 图 2 新型单相光伏并网控制框图 Fig. 2 Diagram of novel single-phase photovoltaic grid-connected control 直流侧电压外环的作用是控制并网逆变器直 流侧电压 Udc 的稳定，间接控制了光伏组件阵列的 输出功率，在电网电压保持稳定的情况下，即确定 了并网有功电流幅值 * spI ，保证了阵列输出功率与并 网有功功率平衡， * 3.2 功率环 dcU 是 Udc 的参考值。 由于电网电压 us 变化不大，可以把功率环的有 功和无功功率 Ps、Qs 调节转化为网侧电流的有功和 无功电流 Isp、Isq 控制。由于 Isp 和 Isq 是直流量，PI 控制器能保证网侧电流的控制精度和功率因数。在 图 3(a)中，Isp 和 Isq 与各自的参考值 * sqI 作差， 两者差值 spe 、 sqe 经过 PI(dc)调节后，经过变换矩阵 pq αβ−C sqI 的取值 由式(6)确定， sQ∗ 将在第 4 节讨论。 可得到电容电流内环的参考值 * spI 、 * ci 。 * G s ( ) s = K s p + s K i s (5) I * sq = * Q U 2 s / s (6) e sp e sq ⎡ ⎢ ⎣ ⎤ ⎥ ⎦ = I I * sp * sq ⎡ ⎢ ⎢ ⎣ ⎤ ⎥ ⎥ ⎦ − I I ⎡ ⎢ ⎢ ⎣ sp sq ⎤ ⎥ ⎥ ⎦ = C − αβ pq ⎡ ⎢ ⎢ ⎣ * i s α * i s α ⎤ ⎥ ⎥ ⎦ − C − αβ pq i s α i s β ⎡ ⎢ ⎢ ⎣ ⎤ ⎥ ⎥ ⎦ = C − αβ pq * i s α * i s β ⎡ ⎢ ⎢ ⎣ − − i s α i s β ⎤ ⎥ = ⎥ ⎦ C − αβ pq e s α e s β ⎤ ⎥ ⎥ ⎦ ⎡ ⎢ ⎢ ⎣ (7) 锁相环 us ω0t isα isβ 构造 两相 正交 电流 Cαβ−pq * spI + − − + Isp Isq esp esq * spI (a) 原功率环 ω0t up uq Cpq −αβ * * i iα = c c * ci β Gs(s) Gs(s) 锁相环 us 构造 两相 正交 电流 − isα isβ − + ω0t * si α + esα esβ Cαβ−pq ω0t esp esq Gs(s) Gs(s) up uq Cpq −αβ * * i iα = c c * ci β * si β is is (b) 等效功率环 图 3 功率环结构图 Fig. 3 Power loop structure 由式(7)可知，图 3(a)和(b)是等效的，并可得有 功和无功电流差值 esp、esq 的时域表达式： e sp e sq ⎧⎪ ⎨ ⎪⎩ t ( ) t ( ) t t e ( )sin ω = − s 0 α t t e ( )cos ω = − s 0 α e s β e − s β t t ( )cos ω 0 t t ( )sin ω 0 (8) 由图 3 (b)可得功率环 PI(s)控制器输出量 up、uq 的时域表达式： u t ( ) ⎧⎪ p ⎨ u t ( ) ⎪⎩ q = = e sp e sq t ( ) t ( ) ∗ ∗ g t ( ) s g t ( ) s (9)
    20 中 国 电 机 工 程 学 报 第 31 卷 式中：“∗ ”表示卷积乘法； s( ) 达式。 g t 为 s ( )G s 的时域表 功率环控制输出量 up、uq 经过变换矩阵 pq αβ−C 可得电流内环的参考值 * ci α 、 * ci β的时域表达式： * i t ( ) ⎧ ⎪ c α ⎨ * i t ( ) ⎪⎩ c β t u t ( )sin( ) = − ω p 0 t u t ) ( )cos( = − ω 0 p t u t ( )cos( ) ω 0 q t u t ( )sin( − ω 0 q ) (10) 对式(10)两边进行拉普拉斯变换，可得 * ci α 、 * ci β 的 s 域表达式： * t s u t ] L[ ( ) L[ ( )sin = − ω c 0 p α * t s u t ( )cos ] L[ ( ) L[ = − − ω c p 0 β I I ⎧ ⎪ ⎨ ⎪⎩ U t ( )cos q u t ( )sin q t ] ω 0 t ] ω 0 (11) 式中“L”为拉普拉斯算子。 把式(8)代入式(9)，然后进行拉普拉斯变换，又 知 2 个信号在时域中卷积的频谱等于 2 信号在 s 域 中频谱的乘积，可得 up、uq 的 s 域表达式： t G s t e ( )cos ( ) ⎤ ω ⎦ s 0 β t G s e t ( )sin ( ) ⎤ ω − ⎦ s 0 β t t e ( )sin ω − s 0 α t t e ( )cos ω − s 0 α ( ) L ( ) L ⎧ U s ⎪ ⎨ U s ⎪ ⎩ = = ⎡ ⎣ ⎡ ⎣ (12) p q s s 根据 s 域卷积的频移特性，如下式(13)，可把 式(12)化简整理，代入式(11)，可推导出式(14)。 I ⎧ ⎪⎪ ⎨ ⎪ ⎪⎩ ⎧ ⎪ ⎪ ⎪ ⎪ ⎨ ⎪ ⎪ ⎪ ⎪ ⎩ I [ L ( )sin f t t ω 0 ] = [ L ( )cos f t t ω 0 ] = j 2 1 2 s s [ [ E s G s ( ) ( s α 1 2 E s G s ( ) ( s β j 2 E s G s ( ) ( s β E s G s ( ) ( s α [ [ s s * s ( ) c α * s ( ) c β = j 2 = 1 2 将式(5)代入式(14)整理可得 [ F s ( + j ω 0 ) − F s ( − j ω 0 ) ] [ F s ( + j ω 0 ) + F s ( − j ω 0 ) ] + j ω 0 ) + G s ( s − j ω 0 ) ] − (13) (14) + j ω 0 ) − G s ( s − j ω 0 ) ] + j ω 0 ) − G s ( s − j ω 0 ) ] + + j ω 0 ) + G s ( s − j ω 0 ) ] 2 s p = + K I I ⎤ ⎥ ⎥ ⎦ ⎡ ⎢ ⎢ ⎣ * s ( ) c α * s ( ) c β s K s i 2 s ω + 0 s K ω i 0 2 2 + ω 0 3.3 电容电流环 ⎡ ⎢ ⎢ ⎢ ⎢ ⎢ ⎣ s − s K s p + s K ω i 0 2 2 ω + 0 s K s i 2 + ω 0 s 2 E s ( ) s α E s ( ) s β ⎤ ⎥ ⎦ ⎡ ⎢ ⎣ (15) ⎤ ⎥ ⎥ ⎥ ⎥ ⎥ ⎦ 功率环之后可以用来作为内环控制的变量有 iI、u1(表示 L1 和 R1 之间的端电压)、ic 和 uc，但只 有电容电流 ic 可以帮助提高控制系统的动态性能和 稳定性[3,8]。电容电流环只采用比较调节器 P(c)，内 环的稳态误差不影响外环的控制精度。 3.4 控制参数设计 外环决定控制系统的调节精度，内环确定系统 的稳定性，本文只考虑功率环和电流环控制参数对 系统稳定性的影响。假设直流侧电压稳定和开关频 率足够高，那么并网逆变器可以等效为一个比例环 节 KPWM，内环的控制输出量可看成是并网逆变器 交流侧电压 uI。根据式(15)，图 2 中的功率环和电 容电流环可以等效成图 4。式(15)右侧被乘矩阵第 1 行 2 个表达式在低频段中表现的幅频特性相近，假 设 Esβ(s)为零不影响系统的稳定性分析结果。由式 (15)可得功率环的等效控制器见式(16)。等效电流控 制的传递函数如式(17)所示，系统电路电气元件参 数如表 1 所示。电网电压可视为外界干扰，令 Us(s)=0，等效电流控制的开环传递函数和闭环传递 函数分别如式(18)和(19)所示。 s K s i 2 2 s ω + 0 (16) G s ( ) K = + s p ′ s c p 2 E s G s K K ( ) ( ) ′ = PWM s s c U s L C s R K C s ) 1] ( ) ( [ + + p s 1 f 1 f 2 3 I s a s a s a s a s ( ) ( + + + 0 1 s 3 2 c L L C a R K L C a ( ) = = + ； 其 中 ， 3 1 2 f f 1 p 2 c a R K C R R C L a + 。 = + ； 0 2 f 1 2 f 1 p 2 + 2 R R 1 2 + 0 ) L 1 = + + + (17) R L C 2 1 f ； G s ( ) so = s I ( ) s E s ( ) = 5 a s 3 + 4 a s 2 + p cK K s 2 K s ( PWM p 3 2 s a a ( ) + + ω 3 1 0 + a ( 0 s K s K + i 2 a + ω 0 2 s 2 ω p 0 2 s ) ) + 2 a ω ω 1 0 s a + 0 2 0 (18) is − es * si + s( )G s′ * ci + − ci P(c) KPMW is − ic iI + uI + − uc 1 sL+ 1 R 1 1 sC f uc + − us 1 sL+ 2 R 2 is 图 4 等效电流控制结构图 Fig. 4 Structure diagram of equivalent current control
    第 21 期 彭双剑等：LCL 滤波器的单相光伏并网控制策略 21 * Q U I s = s 2 nom 2 ⎛ − ⎜ ⎝ U I PV PV U s ⎞ ⎟ ⎠ (20) 式中 nomI 为并网逆变器的额定电流。 小型光伏发电系统在电网中看成为一个负载，当 将来小型发电系统普及后，为了不影响电网的性 质，可以特意控制网测电流滞后电网电压，使光伏 发电系统当作为感性负载，这里 * sQ 取 150 var。 5 仿真与实验 用 Matlab/Simulink 建立了系统仿真模型，图 1 所示电路电气元件的参数如表 1 所示。MPPT 控制 采用恒电压控制， PVU 的参考值为 200 V。 * dcU 取值 为 400 V。直流侧电压控制环的控制参数 dc pK =0.5， iK =100。 dc 表 1 系统参数 Tab. 1 System parameters 值 3 000 5.0 0.15 220 符号 Cf/μF L2/mH R2/Ω ω0/(rad/s) 符号 Cdc/μF L1/mH R1/Ω Us/V 值 15 2.5 0.10 314 仿真初始条件是环境温度 25 ℃、光照强度 1 000 W/m2，0.4 s 时光照强度突变为 500 W/m2。为 了便于观察，图 6 中的电网电压 us 幅值在实际值基 础上缩小 10 倍。由图 6 可知，当光照强度变化时， 系统具有良好的动态响应速度。由图 7 可知，在 2 种光照强度情况下，网侧电流 is 的畸变率均小于国 家标准 5%。图 8 中，实线分别表示光伏发电功率 PVP 和无功功率参考值 * sQ ，虚线分别表示并网实际 有功功率 sP 和无功功率 sQ ，由图 8 可知，控制系统 能使并网功率 sP 、 sQ 精确跟踪参考功率 PVP 、 * sQ ， 但是在动态调节过程中有功和无功功率存在耦合。 G s ( ) c s = s G s ( ) o s G s ( ) + o 1 (19) pK 、 s iK 、 p 在 Matlab 环境下计算闭环传递函数(见式(19)) cK 下的闭 的极点分布，得不同控制参数 s iK 、 p cK 不变，而 s 环极点，如附表 A1 所示。当 s pK 增大到 2 时，系统闭环极点有一对共轭闭环极点的 实部为正，即这对极点落在 s 右半平面，此时系统 cK 时，在 是不稳定的；当 s 一定取值范围内有益于提高系统的稳定性。不同电 cK 下，对系统开环传递函数(见 容电流环比例增益 p cK 的增大可以增 式(18))作波特图，如图 5 所示， p 加系统开环增益，能抑制 LCL 滤波器的谐振尖峰。 cK 分别取值为 0.5、200、50， 综上分析， s pK 不变，分别增大 s iK 、 p pK 、 s iK 、 p 此时系统开环传递函数的幅值裕度和相角裕度分别 为 8.75 dB 和 37.7°，稳定裕度满足工程应用的需要。 B d / 值 幅 ) ° ( / 角 相 200 100 0 −100 0 −90 −180 −270 10−1 25 50 5 5 25 50 100 101 102 频率/Hz 103 104 105 图 5 在不同电容电流环比例增益下的开环传递函数波特图 Fig. 5 Bode diagram of open loop transfer function under different proportional gains in capacitor current loop 4 系统功能扩展 本系统的基本功能是光伏并网发电，在设计光 伏并网发电系统时，并网逆变器容量的配置主要由 光伏组件阵列的峰值功率确定的，光伏组件的峰值 功率是在环境温度 25℃、光照强度 1000 W/m2 测得 的出厂值，实际上光伏组件的工作环境通常不会达 到能让它输出峰值功率的理想条件，因此，通过并 网逆变器变换的功率一般不会达到它的额定容量。 为了提高并网逆变器的利用率，剩余容量可用来实 现其他的功能，如谐波抑制[18]、无功补偿[13,19]、电 压控制[20]等。这里在首先满足光伏发电功率最大输 出时，可以考虑用剩下的容量作为补偿无功功率的 开销，补偿无功量由式(20)确定。
    22 中 国 电 机 工 程 学 报 第 31 卷 / % 值 幅 / % 值 幅 100 80 60 40 20 0 0 100 80 60 40 20 0 0 基波幅值(50Hz)=12.62A 总畸变率=1.82% 200 400 f/Hz 600 800 1 000 (a) 光照强度 1 000 W/m2 基波幅值(50Hz)=6.163A 总畸变率=2.90% 200 400 f/Hz 600 800 1 000 (b) 光照强度 500 W/m2 图 7 网侧电流的频谱图 Fig. 7 Grid-side current spectrums W P / 3 000 2 000 1 000 0 0.2 Ps Ppv 0.3 0.4 0.5 0.6 0.7 t/s (a) 有功功率对照 r a v / Q 400 200 0 0.2 Qs Qs * 0.3 0.4 0.5 0.6 0.7 t/s (b) 无功功率对照 图 8 并网有功和无功功率的跟踪效果 Fig. 8 Tracking results of grid-connected active and reactive power 为验证仿真结果，搭建了光伏组件阵列峰值功 率为 2 kWp 的实验样机，如图 9 所示。 (a) 光伏组件阵列 (b) 控制系统 图 9 样机实物图 Fig. 9 Prototype photos 样机采用三菱功率模块 PM50B5LA060 为并网 逆变器的功率模块，控制算法在 TMS320F28335 DSP 实现。光伏组件采用 CS48-TD85，共 24 块， 12 块串联成 1 组，共 2 组，2 组并联组成光伏组件 阵列。 实验结果如图 10 所示，实际发电功率(0.95 kW) 接近额定功率一半时，此时网侧电流的谐波畸变率 为 2.8%，低于国家标准 5%。无功功率参考值设为 150 var，由图 10(a)可知，此时实际并网无功功率为 0.16 kvar，由此可知，并网无功是可以调节的，且 功率因数为 0.99。 0.96kVA 0.95kW 0.16 var 50 Hz ) ) / 格 V 0 0 2 ( u / 格 A 0 1 ( i u i t(1.6 ms/格) (a) 功率信息和电网电压和网侧电流波形 / % 值 幅 100 50 0 1 9 17 33 41 49 25 谐波次数 (b) 网侧电流的频谱分析 图 10 实验结果 Fig. 10 Experiment results 6 结论 分析了和设计了基于 LCL 滤波器的单相光伏 并网控制方法，得出如下结论： 1）功率环比例增益的选取对系统稳定性影响 较大，电容电流环比例增益的增大可增加系统开环 增益并能抑制 LCL 滤波器引起的谐振尖峰。 2）所提控制方法让单相光伏发电系统具备无 功功率补偿能力。 3）控制参数设计过程中，没有考虑引入无功 功率调节通道对系统稳定性的影响，本文将在以后 研究。 参考文献 [1] Zmood D N，Holmes D G，Bode G H．Frequency-domain analysis of three-phase linear current regulators[J]．IEEE Trans. on Industrial Electronics，2001，37(2)：601-610． [2] Twining E，Holmes D G．Grid current regulation of a three-phase voltage source inverter with an LCL input filter[J]．IEEE Trans. on Power Electronics，2003，18(3)： 888-895． [3] Loh P C，Holmes D G．Analysis of multiloop control strategies for LC/CL/LCL-filtered voltage-source and current-source inverters[J] ．IEEE Trans. on Industrial Electronics，2005，41(2)：644-654． [4] 曹陆萍，沈国桥，朱选才，等．单相并网逆变器功率控
    第 21 期 彭双剑等：LCL 滤波器的单相光伏并网控制策略 23 制的实现[J]．电力电子技术，2007，41(9)：19-20． Cao Luping，Shen Guoqiao，Zhu Xuancai，et al．Power control of single phase grid-connected inverter[J]．Power Eectronics，2007，41(9)：19-20(in Chinese)． [5] 吴春华，陈国呈，丁海洋，等．一种新型光伏并网逆变 器控制策略[J]．中国电机工程学报，2007，27(33)： 103-107． Wu Chunhua，Chen Guocheng，Ding Haiyang，et al．A novel control strategy for photovoltaic grid-connected inverter[J]．Proceedings of the CSEE，2007，27(33)： 103-107(in Chinese)． [6] 刘飞，徐鹏威，陈国强，等．基于 LCL 滤波器的三相 光伏并网控制系统研究[J]．太阳能学报，2008，29(8)： 965-971． Liu Fei，Xu Pengwei，Chen Guoqiang，et al．Study on three-phase photovoltaic grid-connected control system with LCL filter[J]．Acta Energiae Solaris Sinica，2008， 29(8)：965-971(in Chinese)． [7] 沈国桥，徐德鸿．LCL 滤波并网逆变器的分裂电容法 电流控制[J]．中国电机工程学报，2008，28(18)：36-41． Shen Guoqiao ， Xu Dehong ． Current control for grid-connected inverters by splitting the capacitor of LCL filter[J]．Proceedings of the CSEE，2008，28(18)：36-41(in Chinese)． [8] 徐志英，许爱国，谢少军．采用 LCL 滤波器的并网逆 变双闭环入网电流控制技术[J]．中国电机工程学报， 2009，29(27)：36-41． Xu Zhiying，Xu Aiguo，Xie Shaojun．Dual-loop grid current control technique for grid-connected inverter using an LCL filter[J]．Proceedings of the CSEE，2009，29(27)： 36-41(in Chinese)． [9] 王飞，余世杰，苏建徽，等．光伏并网发电系统的研究 及实现[J]．太阳能学报，2005，26(5)：605-608． Wang Fei，Yu Shijie，Shen Yuliang，et al．Study and realization of photovoltaic grid-connected power system [J]．Acta Energiae Solaris Sinica，2005，26(5)：605-608(in Chinese)． [10] 王飞，谢磊，周毅人，等．单相光伏并网逆变器的控制 策略研究及实现[J]．电力电子技术，2009，43(11)：24-25． Wang Fei，Xie Lei，Zhou Yiren，et al．Study and realization of photovoltaic grid-connected power system [J]．Power Electronics，2005，26(5)：605-608(in Chinese)． [11] 姜世公，王卫，王盼宝，等．基于功率前馈的单相光伏 并网控制策略[J]．电力自动化设备，2010，30(6)：16-22． Jiang Shigong ， Wang Wei ， Wang Panbao ， et al ． Power-feedforward-based control strategy of grid-connected single-phase PV system[J]．Electric Power Automation Equipment，2010，30(6)：16-22(in Chinese)． [12] 张超，何湘宁．短路电流结合扰动观察法在光伏发电最 大功率点跟踪控制中的应用[J]．中国电机工程学报， 2006，26(20)：98-102． Zhang Chao，He Xiangning．Short-current combined with perturbation and observation maximum-power-point tracking method systems [J]．Proceedings of the CSEE，2006，26(20)：98-102(in Chinese)． for photovoltaic power [13] 吴理博，赵争鸣，刘建政，等．具有无功补偿功能的单 级式三相光伏并网系统[J]．电工技术学报，2006，21(1)： 28-32． Wu Libo ， Zhao Zhengming ， Liu Jianzheng ， et al ． Implementation of a single-stage three-phase grid-connected photovoltaic system with reactive power compensation[J]．Transactions of China Electrotechnical Society，2006，21(1)：28-32(in Chinese)． [14] 周德佳，赵争鸣，袁立强，等．具有改进最大功率跟踪 算法的光伏并网控制系统及其实现[J]．中国电机工程学 报，2008，28(31)：94-100． Zhou Dejia ， Zhao zhengming ， Yuan Liqiang ， et al ． Implementation of a photovoltaic grid-connected system based on improved maximum power point tracking[J]．Proceedings of the CSEE，2008，28(31)： 94-100(in Chinese)． [15] 杨水涛，张帆，丁新平，等．基于输入-输出参数的光 伏电池最大功率控制的比较[J]．电工技术学报，2009， 24(6)：95-102． shuitao ， Zhang Fan ， Dingxinping ， et Yang al．Comprehensive research on the photovoltaic maximum power point tracking based on input parameters or output parameters[J] ． Transactions of China Electrotechnical Society，2009，24(6)：95-102(in Chinese)． [16] Akagi H，Kanazawa Y，Nabae A．Instantaneous reactive power compensators comprising switching devices without energy storage components[J]．IEEE Trans. on Industry Applications，1984，IA-20(3)：625-630． [17] 李圣清，朱英浩，周有庆，等．基于瞬时无功功率理论 的四相输电谐波电流检测方法[J]．中国电机工程学报， 2004，24(3)：12-17． Li Shengqing ， Zhu Yinghao ， Zhou youqing ， et al．Four-phase transmission harmonic current detection method based on instantaneous reactive power theory [J]．Proceedings of the CSEE，2004，24(3)：12-17 (in Chinese)． [18] 张强，刘建政，李国杰．单相光伏并网逆变器瞬时电流 检测与补偿控制[J]．电力系统自动化，2007，31(10)： 50-54． Zhang Qiang，Liu Jianzheng，Li Guojie．Instantaneous
    24 中 国 电 机 工 程 学 报 第 31 卷 current detection and compensation of single-phase phtotovolatic grid-connected inverter[J]．Automation of Electric Power Systems，2007，31(10)：50-54(in Chinese)． [19] 王海宁，苏建徽，张国荣，等．光伏并网发电及无功补 偿的统一控制[J]．电工技术学报，2005，20(9) 114-118． Wang Haining，Su Jianhui，Zhang Guorong，et al．Unitive control of PV grid connected generation and reactive compensation[J]．Transactions of China Electrotechnical Society，2005，20(9)：114-118(in Chinese)． 彭双剑 [20] Mastromauro R A，Liserre M，Kerekes T，et al．A single-phase grid-connected photovoltaic system with power quality conditioner functionality[J]．IEEE Trans. on Industrial Electronics， 2009，56(11)：4436-4444． voltage-controlled 收稿日期：2011-05-06。 作者简介： 彭双剑(1984)，男，博士研究生，2006 年 6 月毕业于湖南大学自动化专业，获学 士学位；2006 年 9 月起开始攻读湖南大学 电气工程专业博士学位，主要研究方向为 新能源并网发电控制技术、微网控制技术 和 电 能 质 量 控 制 技 术 ； shuangjian16@ 163.com； 罗安(1957)，男，教授，博士生导师， 主要从事电能质量控制和微网控制的理论 和技术等方面的教学与科研工作； 荣飞(1978)，男，湖南长沙人，博士， 副教授，主要从事新能源发电并网控制和 微网控制的理论和技术等方面的教学与科 研工作。 (责任编辑 王剑乔) 附录 A s pK 增大； s iK 、 c pK 不变 表 A1 不同控制参数下的闭环极点 Tab. A1 Closed-loop poles under different control gains 0.1 100 1.0×104 25 0.5 100 1.0×104 25 1 100 1.0×104 25 2 25 100 1.0×104 −0.0489+1.3471i −0.0489−1.3471i −0.0066 −0.0021+0.0403i −0.0021−0.0403i −0.1664+1.3156i −0.1664−1.3156i −0.1547 −0.0107+0.0318i −0.0107−0.0318i −0.0803+1.3247i −0.0803−1.3247i −0.3381 −0.0050+0.0315i −0.0050−0.0315i 0.0663+1.3777i 0.0663−1.3777i −0.6364 −0.0025+0.0314i −0.0025−0.0314i 0.5 1 25 0.5 25 0.5 50 25 0.5 10 1.0×104 −0.1662+1.3168i −0.1662−1.3168i −0.1744 −0.0010 + 0.0316i −0.0010−0.0316i 1.0×104 −0.1663+1.3163i −0.1663−1.3163i −0.1662 −0.0050+0.0320i −0.0050−0.0320i s iK 增大； s pK 、 c pK 不变 1.0×104 −0.1662+1.3169i −0.1662−1.3169i −0.1762 −0.0001+0.0314i −0.0001−0.0314i 25 200 1.0×104 −0.1665+1.3143i −0.1665−1.3143i −0.1232 −0.0263+0.0270i −0.0263−0.0270i c pK 增大； s pK 、 s iK 不变 0.5 200 1.0×104 1 0.5 200 1.0×104 5 0.5 200 1.0×104 50 0.5 100 200 1.0×104 −0.0089+1.3482i −0.0089−1.3482i −0.0011+0.0351i −0.0011−0.0351i −0.0087 −0.0356+1.3466i −0.0356−1.3466i −0.0094+0.0434i −0.0094−0.0434i −0.0189 −0.3117+1.2125i −0.3117−1.2125i −0.0225+0.0251i −0.0225−0.0251i −0.3405 −0.3319+0.8773i −0.3319−0.8773i −0.0211+0.0246i −0.0211−0.0246i −1.3026
    分享到：
    赞 收藏

    相关推荐

    资料库

    开发技术

    共收录19306份资料，累计14个分类，关注成员有19位，主要包括：Actionscript,Javascript,PHP,VB,Perl,Delphi,Python,C#,C,Java,C++,Web开发,硬件开发,其它

    热门标签

    Actionscript Javascript PHP VB Perl Delphi Python C# C Java C++ Web开发 硬件开发 其它

    最新资料