基于改进遗传算法的移动机器人路径规划 郭首亮，孙海洋，陈 珍 (南京大学金陵学院信息科学与工程学院，南京 210089) 摘要：为了解决传统遗传算法在移动机器人路径规划中，在对路径长度，路径平滑度以及路径安全度进行多目 标优化时，难以找到合适的比例因子的问题。本文提出了一种改进的遗传算法，在传统的遗传算法选择，交叉，变 异的基础上，增加了基因定向变异，将多目标优化转换成单目标优化，有效地解决了比例因子的难以寻找的问题。 最后在模拟环境下利用 Matlab 进行仿真，证明了这一改进遗传算法的高效性，可行性。 关键词：遗传算法；机器人路径规划；基因定向变异；Matlab 仿真 中图分类号： 文献标志码：A Path Planning Method for Mobile Robot Based on Improved Genetic Algorithm (Information Science and Technology Academy, Nanjing University Jinling College, Nanjing 210089, China) Guo Shouliang, Sun Haiyang, Chen Zhen Abstract:In order to resolve the problem conventional genetic algorithm caused in planning an appropriate path for mobile robot that it is a great challenge to find a well-matched scale factor when we try to shorten the length of path, smoothen the path and increase the security of the path, in this paper, an improved genetic algorithm is proposed, which, based on orthodox genetic algorithm in terms of algorithm selection, crossover and mutation, increases the possibility of genetic oriented-mutation and simplifies the multi-target optimization into mono-target one. Whereby the improved path planning method, the problem of finding a well-matched scale factor can be settled efficiently. And it can be proved through Matlab simulation that this improved genetic algorithm is of great efficiency and practicability. Keywords: genetic algorithm;path planning for mobile robot;genetic oriented-mutation;Matlab simulation. 0 引言 目前，人工智能和机器人学[1]的发展极为迅速， 移 动 机 器 人 的 路 径 规 划 问 题 是 其 中 重 要 的 研 究 部 分。所谓路径规划，就是在一定的约束条件下，寻 找出一条从起始点到目标点的最佳路线。一般的约 束条件主要包括：最短行驶路径，最短行驶时间， 最高路径平滑度，最高路径安全度和最低路径行驶 能量等。所以，大多路径规划均是多目标优化问题， 但是如何寻找到这些约束条件之间的关系，去构造 合适的目标函数，往往成为研究的难点所在。 在移动机器人路径规划[2]的研究领域中，典型 的规划方法有 A*算法，D*算法，蚁群算法[3]，人工 势场法，可视图法和遗传算法[4-6]等。其中，遗传算 法（GA）是一种借鉴生物界自然选择和遗传机制的 随机并行搜索算法，对于传统搜索方法难以解决的 非线性问题和复杂问题具有良好的鲁棒性，灵活且 不易落入种群局部最小点等优点。但众多研究表明， 传统遗传算法在进行机器人路径规划时，存在种群 规模大，收敛速度慢，容易陷入局部极小点等问题。 针对这些问题，笔者通过加入基因定向变异的方法， 提高避障能力，使得适应度函数中仅为最短路径长 度，简化目标函数，并且可以选取适应度更高的个 体。 1 直角坐标法环境建模 1.1 建模前提 笔者的研究重点是在全局信息已知的前提下， 寻找一条从起始点到目标点最短避障路径。所以， 将机器人视为一个质点，不考虑实际环境中地面高 低变化，将所有障碍物视为圆形障碍。 图 1 直角坐标法建立的环境模型 1.2 环境描述 在 Matlab 中，经过编程的环境模型如图 1 所示， 坐标左下角为起点，右上角为终点，圆形为障碍物。 其中，对这个直角坐标的 X 轴进行等间隔划分，且 划分间隔不大于圆形障碍物的最小直径。对 Y 轴不 进行划分，可取任意实数。 

2 基于改进遗传算法的路径规划方法 2.1 个体编码 笔者改进的遗传算法的每一条路径相当于一个 染色体，同生物体一样，希望通过这些染色体的进 化来找出一条能够避开障碍物并且最短的路径。由 笔者设计的环境模型可以知道，每条路径均是由十 进制实数串构成，直接作为染色体，对其使用遗传 算子。个体编码方式如图 2 所示，其中，x 为行坐 标，y 为纵坐标。 y i    y d R i 10 ( 1) y  i  iR ,  rand , d R  （3） [( ),( , x y 2 2 ) , )] , x y x y 1 1 n 图 2 个体编码方式示意图 ( m 2.2 初始种群的产生 初始种群作为遗传算法计算的起点，该种群必 须要能够含有最佳路径的所有优良因子，所以初始 种群中的个体应当有数量上的保证，才能覆盖到整 个搜索空间。如图 3 所示，笔者设计的初始种群中 的个体均是由随机数构成，且保证足够的数量。 图 3 初始种群示意图 2.3 基因定向变异 初始种群中每个个体均是由基因片段组成，而 每 个 基 因 片 段 在 路 径 中 的 体 现 就 是 两 点 构 成 的 线 段。通过判断每条线段是否经过障碍物来决定是否 需要对该基因片段进行变异，即改变点的坐标。下 面不妨设该基因片段的两个点的坐标为： ( x 则可以得到该基因片段的直线方程，如下所示：  和 1 ) 。 y x y ) ( , , 1  i i i i y  y i x i   y i x i 1  1  ( x  x i )  y i （1） 由式（1）可以得到障碍物点(x,y)到该线段的距离 d 为： ( y i y i y i y i   x 1  1  ) ) d  y   ( y  i ( x y i i 2 ) y i 1   1 1   （2） R 为安全距离，i 为大于 1 的实数，定义基因定向变 异的方式为： 图 4 基因定向变异示意图 如图 4 所示，基因定向变异通过改变某一劣质基因 片段，保留原有的优良特性，并且解决了安全距离 问题，使得适应度函数由多目标优化问题转化为单 目标优化问题，更为简便。 2.4 适应度函数的计算 由于基因定向变异的引入，使得适应度函数无 需考虑避障问题，因此使得适应度的计算大为简便， 加快了遗传算法的收敛速度，此处我们仅考虑最短 路径，则有适应度函数: ( ) f x  1 2 ) ( x i  x i 1   ( y i  y i 1  2 ) (4) n  i 1  其中，n 为种群个体中基因片段数。 2.5 遗传算子 1）选择 遗传算法通过使用选择算子对种群中的个体进 行优胜劣汰操作，使得适应度大的个体遗传到下一 代概率较大，适应度较低的遗传到下一代概率较小。 笔者采用轮盘赌选择方法，每个个体进入下一代的 概率等于该个体的适应度值占整个种群适应度和的 比例，因此，适应度值越高，被选中的概率越大。 2）交叉 交叉又称为重组，是按照较大的概率从种群中 选择两个个体，交换这两个个体中的某些位。笔者 采用的是较为简便的单点交叉，在个体编码串中随 机设立一个交叉点，然后在该点相互交换两个个体 的部分染色体。 3）变异 变异是以较小概率对个体编码串中的某些位进 行改变，一方面是为了改善遗传算法的局部搜索能 力，另一方面是为了维持群体的多样性，防止出现 早熟现象。 2.6 终止条件 终止条件是遗传算法结束的条件，此处笔者采 用最大遗传代数作为终止条件，结束过早或过晚都 会影响遗传算法的结果，因此需要实验进行验证。 

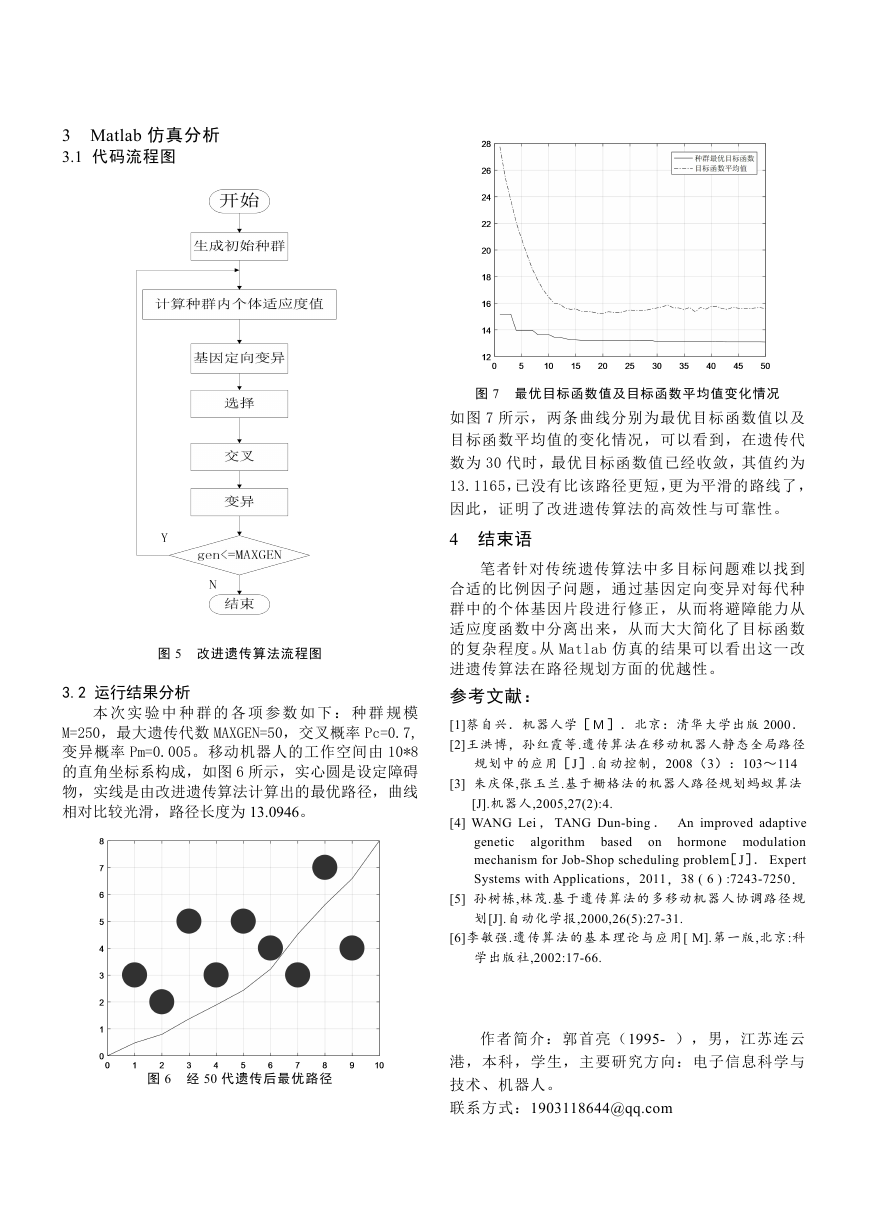
3 Matlab 仿真分析 3.1 代码流程图 图 5 改进遗传算法流程图 3.2 运行结果分析 本 次 实 验 中 种 群 的 各 项 参 数 如 下 ： 种 群 规 模 M=250，最大遗传代数 MAXGEN=50，交叉概率 Pc=0.7, 变异概率 Pm=0.005。移动机器人的工作空间由 10*8 的直角坐标系构成，如图 6 所示，实心圆是设定障碍 物，实线是由改进遗传算法计算出的最优路径，曲线 相对比较光滑，路径长度为 13.0946。 图 7 最优目标函数值及目标函数平均值变化情况 如图 7 所示，两条曲线分别为最优目标函数值以及 目标函数平均值的变化情况，可以看到，在遗传代 数为 30 代时，最优目标函数值已经收敛，其值约为 13.1165，已没有比该路径更短，更为平滑的路线了， 因此，证明了改进遗传算法的高效性与可靠性。 4 结束语 笔者针对传统遗传算法中多目标问题难以找到 合适的比例因子问题，通过基因定向变异对每代种 群中的个体基因片段进行修正，从而将避障能力从 适应度函数中分离出来，从而大大简化了目标函数 的复杂程度。从 Matlab 仿真的结果可以看出这一改 进遗传算法在路径规划方面的优越性。 参考文献： [1]蔡自兴．机器人学［Ｍ］．北京：清华大学出版 2000． [2]王洪博，孙红霞等.遗传算法在移动机器人静态全局路径 规划中的应用［J］.自动控制，2008（3）：103～114 [3] 朱庆保,张玉兰.基于栅格法的机器人路径规划蚂蚁算法 [J].机器人,2005,27(2):4. algorithm based [4] WANG Lei ， TANG Dun-bing ． An improved adaptive hormone modulation genetic mechanism for Job-Shop scheduling problem［J］． Expert Systems with Applications，2011，38 ( 6 ) :7243-7250． [5] 孙树栋,林茂.基于遗传算法的多移动机器人协调路径规 on 划[J].自动化学报,2000,26(5):27-31. [6]李敏强.遗传算法的基本理论与应用[ M].第一版,北京:科 学出版社,2002:17-66. 作者简介：郭首亮（1995- ），男，江苏连云 港，本科，学生，主要研究方向：电子信息科学与 技术、机器人。 联系方式：1903118644@qq.com 图 6 经 50 代遗传后最优路径