logo资料库

基于贝叶斯网络的故障树分析.pdf

发布时间：2022-06-10 发布人：admin 分类：说明书 资料大小：0.32M 资料格式：pdf 举报 版权申诉
第1页 / 共6页
第2页 / 共6页
第3页 / 共6页
第4页 / 共6页
第5页 / 共6页
第6页 / 共6页
资料共6页，全文预览结束
    2 2 Λ Λ Λ 　2004 年 6 月 文章编号: 1000 6788 (2004) 06 0078 06 系统工程理论与实践 第 6 期　 基于贝叶斯网络的故障树分析 王广彦, 马志军, 胡起伟 (军械工程学院装备指挥与管理系, 河北 石家庄 050003) 摘要: 　文章简要阐述了贝叶斯网络的构造原理和网络信念的传播与更新, 并详细说明了故障树向贝叶 斯网络转化的过程, 主要包括结点与事件的映射关系和联接强度与逻辑门的映射关系 最后通过一个实 例说明了故障树向贝叶斯网络的转化过程, 并对二者的推理功能进行了比较 关键词: 　贝叶斯网络; 故障树分析; 可靠性; 信念 中图分类号: 　TB 114. 3　　　　　　　　文献标识码: 　A 　　　 T he Fau lt T ree A nalysis Based on Bayesian N etw o rk s (D epartm en t of M anagem en t Engineering, Sh ijiazhuang M echan ical Engineering Co llege, Sh ijiazhuang 050003, Ch ina) W AN G Guang yan, M A Zh i jun, HU Q i w ei Abstract: 　 T he bu ilding of netw o rk and the p ropagation and update of netw o rk belief are p resen ted, the converting of fau lt tree to B ayesian netw o rk s is show n, including the m app ing of node to even t and the m app ing of connected in ten sity to logical gate. F inally, tree to B ayesian netw o rk s is illu strated acco rding to a in stance, and their reason ing function s are com pared. Key words: 　B ayesian netw o rk s; fau lt tree analysis; the converting of fau lt reliab ility; belief 1　引言 　　故障树分析法 (FTA ) 是一种对复杂系统的可靠性、安全性进行分析的有效工具, 它把所研究系统的 最不希望发生的故障状态作为故障分析的目标, 然后寻找导致这一故障发生的全部因素, 再找造成这些因 素发生的下一级全部直接因素, 一直追查到那些原始的、无需再深究的因素为止 利用故障树可以分析系 统发生故障的各种途径, 计算各个可靠性特征量, 对系统的安全性和可靠性进行评价 故障树分析法通常适用于故障机理确定、故障逻辑关系清晰的系统, 因为它对系统的故障状态作了很 故障树中的事件都只有两 多假设, 这主要体现在两方面, 即事件状态的二态性和故障逻辑关系的确定性 但很多事件却具有多态性, 比如对于电动机, 它除了故障和正常两种状态外, 还具有 种状态: 故障和正常 故障树中的逻辑门描述的都是确定 低于额定转速的其它故障状态, 而故障树难以描述具有多态性的事件 性的逻辑关系, 需要上一级事件与下一级事件之间具有明确的因果关系 但对于许多复杂系统, 有多种可 能性导致其发生故障, 上一级事件与下一级事件之间不存在确定的因果关系, 这种情况下采用概率的方法 来描述更为合适, 而逻辑门却不具有描述概率的能力 近年来发展起来的贝叶斯网络技术, 从推理机制和系统状态描述上来看, 它和故障树有很大的相似 而且贝叶斯网络还具有描述事件多态性和故障逻辑关系非确定性的能力, 更加适合于对复杂系统的安 本文试图采用贝叶斯网络技术对故障树进行分析, 研究采用贝叶斯网络来描述故 性 全性和可靠性进行分析 障树的可行性, 以展示贝叶斯网络对系统故障状态强大的描述能力 收稿日期: 2003 作者简介: 王广彦 (1976- 01 08 ) , 男 (汉族) , 河北秦皇岛人, 硕士研究生 军 (1974- 唐山人, 硕士研究生 主要从事战场损伤评估方面的研究 ) , 男 (汉族) , 河北邢台人, 讲师 从事维修工程方面的研究, Em ail: w _ g_ y@eyou. com ; 马志 ) , 男 (汉族) , 河北 主要从事战场损伤评估方面的研究; 胡起伟 (1979-
    Λ 第 6 期 2　贝叶斯网络分析原理 Υ Υ 基于贝叶斯网络的故障树分析 97 贝叶斯网络是一种用图表示知识的方法, 并且是可以计算的概率模型 通过这种网络, 可以综合各种 本文主要介绍一下贝叶斯网络的构造原理和网络信念的转播 来源的数据, 并对这些数据进行综合的推理 与更新 2. 1　贝叶斯网络的构造原理 给定一个联合概率分布 P (X 1, X 2, …, X n) 以及变量的一个排序 d 将 X 1 作为根结点开始, 并赋予 X 1 然后用一结点表示 X 2 , 如果 X 2 与 X 1 有关, 从 X 1 到 X 2 建立一联结, 并用 在第 i 级从 X i 的父结 如果 X 2 与 X 1 无关, 则赋予 X 2 以先验概率分布 P (X 2) 条件概率定量表示, { X 1, X 2, …, X i- 1} , 画一组方向线联结到 X i , 并用 P X i 以先验概率分布 P (X 1) X 1) 表示联结强度 P (X 2 点集合 X i X i X i 结果可以得到一个有向非循环图, 可用于表示 P (X 1, X 2, …, X n) 中所体现的许多独立关系, 该图就称作贝 叶斯网络 反过来, P X i 包含有重构原始分布函数所必需的所有信息, 在排序 d 下, 有如下关系, X i P (X 1, X 2, …, X n) = P (X n X n- 1, X n- 2, …, X 1) P (X n- 1 X n- 2, …, X 1) …P (X 3 X 2, X 1) P (X 2 X 1) P (X 1) = P X i i . X i 图 1 是一个典型的贝叶斯网络, 它的联合分布函数为, P (X 1, X 2, X 3, X 4, X 5, X 6) = P (X 6 X 5) P (X 5 X 3, X 2) P (X 4 X 2, X 1) P (X 3 X 1) P (X 2 X 1) P (X 1). 2. 2　网络信念的传播与更新 一旦网络建立, 它可以用于表示领域内的一般知识, 同时可以用作推 理, 贝叶斯网络不只是静态消极地储存一些事实知识, 而且可以作为一种 计算策略对这些知识进行推理 定义信念为 B el (x ) = P (x e) , 即在有已知证据 e 的情况下, 事件 x 发生的条件概率, 反映在一定环境下某一事件发生的可能性 e 可表示为 e = e- x ∪ e+ x , 其中 e- x 反映的是以X 为根结点的子树, e+ x 反 映的是树的其余部分, 则信念可表示为 B el (e) = P (x 式中 = [ P (e- 的 支 持; x , e+ e- x ) ]- 1 为归一化因子 e+ e+ x ) x ) , 表示对诊断 x ) , 表 示 对 预 报 的 支 持, 则 有 B el (x ) = e+ (x ) = P (x 在实际推理过程中, 当观测证据 e 到来时, 网络信念得到更新 (x ) = P (e- e+ x , x ) P (x (x ) (x ) x ) P (x e+ x ) = P (e- x x ) = P (e- x x 令 x 图 1　典型的贝叶斯网络 3　故障树的贝叶斯网络化 从贝叶斯网络的构造原理可以看出, 贝叶斯网络的两大组成要素分别为结点和联接强度, 它们分别对 本文主要讨论结点与事件、联接强度与逻辑门之 应故障树中的事件 (顶事件、中间事件、底事件) 和逻辑门 间的映射关系 3. 1　结点与事件的映射关系 从推理过程和对系统状态的描述过程来看, 贝叶斯网络中的结点与故障树中的事件是一一对应的, 故 然而贝叶斯网络对系统故障状态的描述能力 障树中的事件也正是建立贝叶斯网络所需结点的完整集合 要优于故障树 由于故障树假定所有事件均只有正常和故障两种状态, 所以底事件的状态可用如下变量来描述, x i = 0　 当底事件 i 不发生时 (正常) 1　 当底事件 i 发生时 (故障) 　i = 1, 2, …, n (n 为底事件个数) 顶事件 T 的状态用结构函数 表示, 则 是底事件状态 x i的函数, 记作
    Λ 08 式中 r Λ r Λ Λ r r 系统工程理论与实践 (x ) = (x 1, x 2, …, x n) , (x ) = 0　 当顶事件 T 不发生时 (正常) 1　 当顶事件 T 发生时 (故障) r 2004 年 6 月 　　从上述分析过程可以看到, 故障树假定事件都只有二态性 (正常、故障) 多态性, 可以将故障树中的事件看作是贝叶斯网络中结点概念的特例 述, 贝叶斯网络却能描述事件的 结点的状态可以采用如下变量来描 顶事件 T 的结构函数 可表示为 式中 0　 当事件 i 处于状态 0 1　 当事件 i 处于状态 1 x i = n　 当事件 i 处于状态 n (x ) = (x 1, x 2, …, x n) 0　　 当顶事件 T 处于状态 0 1　　 当顶事件 T 处于状态 1 (x ) = m 　　 当顶事件 T 处于状态m 　　在实际分析过程中, 可以将故障树中的事件直接映射为贝叶斯网络中的结点, 二者在拓扑结构上具有 相似性 3. 2　联接强度与逻辑门的映射关系 故障树中的逻辑门描述的是父子事件之间的故障逻辑关系, 本文只分析两个最关键的逻辑门: 与门和 对于与门, 仅当所有输入事件都发生时, 输出事件才发生; 对于或门, 至少有一个输入事件发生时, 输 逻辑门描述的就是父子事件之间的联接关系, 它与贝叶斯网络中联接强度的概念是相对应 或门 出事件就发生 的 首先分析如何采用联接强度来表示与门 当采用联接强度时, 与门可表示为表 1 所示的条件概率表 与门结构如图 2 所示, 其结构函数为 T = x 0 ∩ x 1 ∩ … ∩ 从与门的条件概率表中可以看到, 只有当所 x n 有的输入变量状态都为 1 时, 输出变量 T 处于状态 1 的概率为 1; 只要有一个变量的状态为 0, 输出变量 T 处于状态 1 的概率就变为 0 正好和与门的结构函数完全对应 表 1　与门的联接强度 (条件概率) X 0 X 1 X n T 1 0 1 0 0 1 1 0 1 1 1 0 1 … … … 0 1 0 1 0 0 1 0 0 1 1 0 1 0 … … … 1 0 0 1 1 0 1 0 1 0 1 0 0 1 0 0 1 再来分析如何采用联接强度来表示或门 当采用联接强度时, 或门可表示为表 2 所示的条件概率表 或门结构如图 3 所示, 其结构函数为 T = x 0 ∪ x 1 ∪ … ∪ 从或门的条件概率表中可以看到, 只有当 x n 所有的输入变量状态都为 0 时, 输出变量 T 处于状态 1 的概率为 0; 只要有一个变量的状态为 1, 输出变量 T 处于状态 1 的概率就变为 1 正好和或门的结构函数完全对应
    Λ 第 6 期 基于贝叶斯网络的故障树分析 18 图 2　与门结构故障树 图 3　或门结构故障树 表 2　或门的联接强度 (条件概率) X 0 X 1 X n T 1 0 1 0 1 0 1 1 0 1 1 0 1 … … … 0 1 1 0 0 1 0 0 1 0 1 1 0 0 … … … 1 0 1 0 1 1 0 0 1 1 0 0 1 0 0 0 1 根据上面的分析过程, 便建立了逻辑门与联接强度之间的映射关系 件, 所以它反映到条件概率表中, 输出事件 T 发生的概率不是 0 就是 1 生的概率属于 (0, 1) 3. 3　故障树与贝叶斯网络的推理过程 由此可见, 逻辑门是联接强度的一种特例 由于逻辑门描述的是确定性事 对于不确定性事件, 输出事件 T 发 从构造和应用方面来看, 故障树与贝叶斯网络非常类似, 它也具有推理的功能, 也是一种知识的表达 当采用故障树进行推理时, 如果从故障树的顶端向下分析, 可以找出系统的故障与哪些底事件有关, 从而全面查清引起系统故障的各种原因; 如果由树的下端往上追溯, 则可以分辨各个底事件对系统的影响 途径和程度, 从而可评价各零部件的故障原因及其对保证系统可靠性、安全性的重要程度 这是故障树的 推理过程 贝叶斯网络不但具有这种推理功能, 而且还可以对各推理要素进行定量描述, 这反映在网络信 念的传播与更新方面 可以将系统的实际症状作为证据 e 加入到网络中, 确定 (x ) (对诊断的支持) 和 (x ) (对预报的支 持) , 从而计算出信念B el (x ) = P (x e) , 这样就对各推理要素通过概率的方式进行了定量描述 4　实例分析 下面通过一个故障树实例来说明故障树向贝叶斯网络的转化过程, 以及贝叶斯网络推理的一些特点 4. 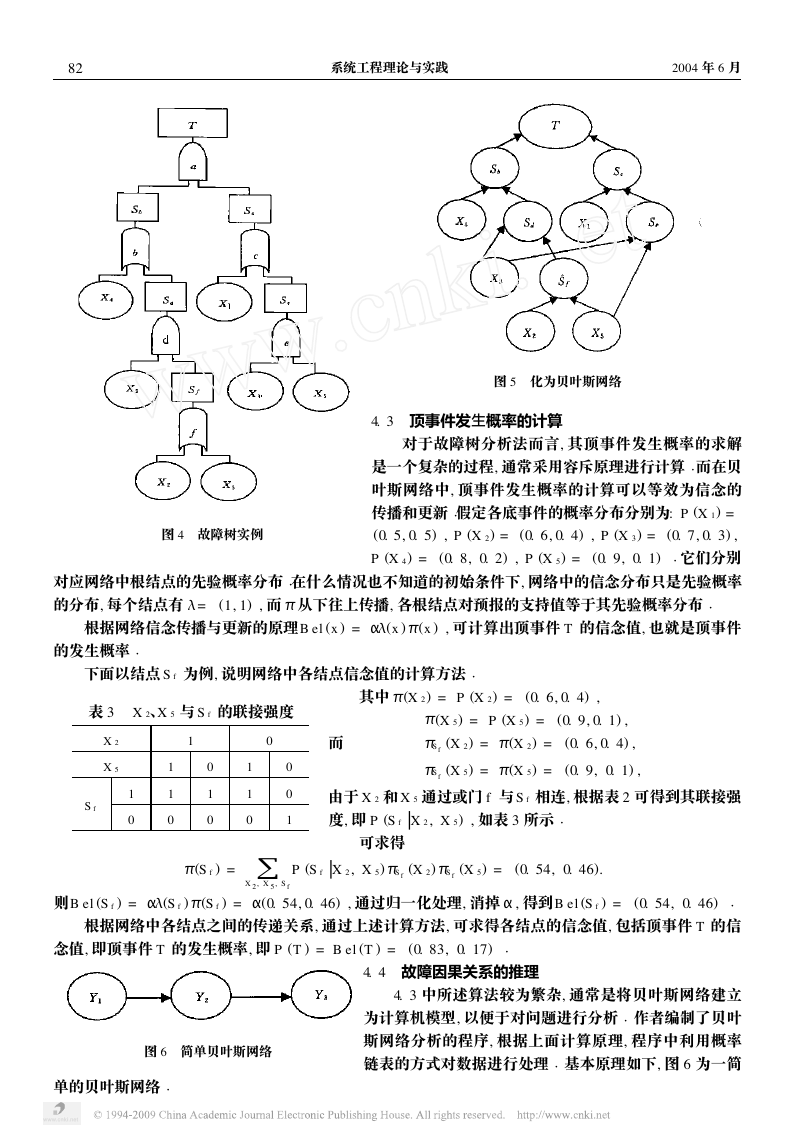1　故障树实例 故障树实例如图 4 所示, 其中 X i 表示底事件 (用圆圈表示) , S i 表示中间事件 (用方框表示) , T 表示 顶事件 4. 2　转化为贝叶斯网络 将上述故障树按 3. 1 和 3. 2 所述的映射关系, 转化为贝叶斯网络, 如图 5 所示 其中故障树中的事件 直接对应网络中的结点, 逻辑门对应网络中相应的联接强度 (方向线)
    Λ 28 Λ Λ 2004 年 6 月 系统工程理论与实践 图 5　化为贝叶斯网络 4. 3　顶事件发生概率的计算 对于故障树分析法而言, 其顶事件发生概率的求解 而在贝 是一个复杂的过程, 通常采用容斥原理进行计算 叶斯网络中, 顶事件发生概率的计算可以等效为信念的 传播和更新 假定各底事件的概率分布分别为: P (X 1) = (0. 5, 0. 5) , P (X 2) = (0. 6, 0. 4) , P (X 3) = (0. 7, 0. 3) , 它们分别 P (X 4) = (0. 8, 0. 2) , P (X 5) = (0. 9, 0. 1) 在什么情况也不知道的初始条件下, 网络中的信念分布只是先验概率 从下往上传播, 各根结点对预报的支持值等于其先验概率分布 图 4　故障树实例 对应网络中根结点的先验概率分布 的分布, 每个结点有 = (1, 1) , 而 根据网络信念传播与更新的原理B el (x ) = (x ) (x ) , 可计算出顶事件 T 的信念值, 也就是顶事件 的发生概率 下面以结点 S f 为例, 说明网络中各结点信念值的计算方法 表 3　 X 2、X 5 与 S f 的联接强度 X 2 X 5 S f 1 0 1 0 而 1 1 0 0 1 0 1 1 0 0 0 1 其中 (X 2) = P (X 2) = (0. 6, 0. 4) , (X 5) = P (X 5) = (0. 9, 0. 1) , S f (X 2) = (X 2) = (0. 6, 0. 4) , S f (X 5) = (X 5) = (0. 9, 0. 1) , 由于 X 2 和 X 5 通过或门 f 与 S f 相连, 根据表 2 可得到其联接强 度, 即 P (S f 可求得 X 2, X 5) , 如表 3 所示 (S f ) = X 2, X 5, S f P (S f X 2, X 5) S f (X 2) S f (X 5) = (0. 54, 0. 46). 则B el (S f ) = (S f ) (S f ) = (0. 54, 0. 46) , 通过归一化处理, 消掉 , 得到B el (S f ) = (0. 54, 0. 46) 根据网络中各结点之间的传递关系, 通过上述计算方法, 可求得各结点的信念值, 包括顶事件 T 的信 念值, 即顶事件 T 的发生概率, 即 P (T ) = B el (T ) = (0. 83, 0. 17) 图 6　简单贝叶斯网络 单的贝叶斯网络 4. 4　故障因果关系的推理 4. 3 中所述算法较为繁杂, 通常是将贝叶斯网络建立 为计算机模型, 以便于对问题进行分析 作者编制了贝叶 斯网络分析的程序, 根据上面计算原理, 程序中利用概率 基本原理如下, 图 6 为一简 链表的方式对数据进行处理
    第 6 期 基于贝叶斯网络的故障树分析 38 每个结点有两种状态: 0 和 1, 其中 P (Y 1) = (0. 3, 0. 7) , P (Y 2 = 0 P (Y 2 = 0 P (Y 3 = 0 P (Y 3 = 0 Y 1 = 0) = 0. 2, P (Y 2 = 1 Y 1 = 1) = 0. 1, P (Y 2 = 1 Y 2 = 0) = 0. 4, P (Y 3 = 1 Y 2 = 1) = 0. 1, P (Y 3 = 1 Y 1 = 0) = 0. 8, Y 1 = 1) = 0. 9, Y 2 = 0) = 0. 6, Y 2 = 1) = 0. 9 Y 1) P (Y 3 若结点 Y 3 的观测值为 (0, 1) , 利用该值去更新概率链表 P (Y 1) P (Y 2 = 0 的项乘以 0, Y 3 = 1 的项乘以 1, 然后对要分析的结点值进行累加, 并进行归一化处理即可 = 1 的概率 Y 2) , 即将该链表中含 Y 3 现分析 Y 1 对 P (Y 1) P (Y 2 Y 1) P (Y 3 Y 2) k ( Y 3 = 0 , 则 k = 0 ; Y 3 = 1 , 则 k = 1 ) 进行归一化处理, 即可得 Y 1, Y 2, Y 3 到 P (Y 1 = 1 e) P (Y 1 = 1 e) = P (Y 1) P (Y 2 Y 1) P (Y 3 Y 2) k Y 1= 1 P (Y 1) P (Y 2 0. 7 × 0. 1 × 0. 6 + 0. 7 × 0. 9 × 0. 1 Y 1) P (Y 3 Y 2) k = 0. 3 × 0. 2 × 0. 6 + … + 0. 7 × 0. 9 × 0. 1 0. 105 0. 165 　　这里简单说明了贝叶斯网络概率更新的基本原理, 采用该方法可实现推理功能 本文 3. 3 中已说明了 故障树也是一种带有推理特点的知识网, 这一点在贝叶斯网络中显得更为突出, 贝叶斯网络正是通过信念 的传播与更新, 定量说明了各结点之间的因果关系, 这相对于故障树较为单一的图形化故障因果关系描述 方式, 更能深刻地阐述系统内的故障因果关系 = 64%. = 例如获得结点 S d 的症状: 其发生故障 通过故障树的推理, 其可以得到这样一些结论: 1) X 3和 S f 肯定 发生了故障; 2) 顶事件 T 受 S d 的影响, 有可能发生故障, 也可能不发生故障, 可能性有多大难以说明; 3) S d 发生故障肯定与 X 2 和 X 5 有关, 但影响程度有多大难以说明 而且反映系统故障原因的深刻程度直接受 分析人员经验的限制 如果采用贝叶斯网络的方法分析故障树, 可以得到更多更为有益的结论 将结点 S d 发生故障这一证 据 e 加入到网络中, 经过信念的传播与更新, 可以得到这样一些结论: 1) X 3和 S f 发生故障的概率为 1; 2) 顶事件 T 受 S d 的影响, 发生故障的概率变为 0. 61; 3) S d 发生故障与 X 2 和 X 5 有关, 其中 X 2 发生故障的概 率为 0. 87, X 5 发生故障的概率为 0. 22; 4) S d 发生故障还对其它一些非直接相关结点产生影响 5　结论 本文通过比较分析, 认为故障树和贝叶斯网络存在很强的相似性, 而且贝叶斯网络还具有描述系统多 态性和故障因果关系非确定性的功能, 因此采用贝叶斯网络方法来描述系统的故障因果关系, 将能更深刻 地揭示系统发生故障的机理 本文简要阐述了贝叶斯网络的构造原理和网络信念的传播与更新, 并详细说明了故障树向贝叶斯网 络转化的过程, 主要包括结点与事件的映射关系和联接强度与逻辑门的映射关系 最后通过一个实例说明 了故障树向贝叶斯网络的转化过程, 并利用贝叶斯网络本身所具有的一些机制, 对故障树和贝叶斯网络的 推理功能作了对比, 证明贝叶斯网络能更为深刻地揭示系统发生故障的前因后果 本文认为采用贝叶斯网络的方法来分析故障树, 能得到更多更为有益的结论 而且二者在构造方法和 推理机制上, 存在先天的相似性, 结合贝叶斯网络来进行故障树分析, 不失为一种对系统可靠性和安全性 进行评价的有效手段 参考文献: [ 1 ]　甘茂治. 军用装备维修工程学[M ]. 北京: 国防工业出版社, 1999. 72- 82. [ 2 ]　杨黎明. 锅炉故障诊断专家系统的研究[D ]. 北京: 清华大学, 1993. 65- 87. [ 3 ]　章国栋. 系统可靠性与维修性的分析与设计[M ]. 北京: 北京航天航空大学出版社, 1990. 107- 148. [ 4 ]　曾亮. 多状态系统故障树的一种生成方法[J ]. 系统工程学报. 1998 (4) : 74- 78.
    分享到：
    赞 收藏

    相关推荐

    资料库

    网络技术

    共收录2367份资料，累计7个分类，关注成员有19位，主要包括：综合布线,网管软件,网络监控,网络设备,其它,系统集成,网络基础

    热门标签

    综合布线 网管软件 网络监控 网络设备 其它 系统集成 网络基础

    最新资料