论文研究-基于改进粒子群算法的滑模控制方案.pdf-资料库

5 Systems Engineering | Theory & Practice Vol.29, No.5 May, 2009 29 2009 5 : 1000-6788(2009)05-0137-05 ! "$#$%&$' 576*8 030024) , , , , 9: -/.,0 (*),+ 1,243 (9:;<=?>A@CBDEFG?>H , XPYNZ r{N ]N¥R¦N§NN¨N© OR[N\P]R^N_N`NaNbNc kRuNvNwNxPyRzN{N|NzN}N~N ]U VRW rR NN®N¯PVRW . ªN«N¬Np ; N®N¯ ; |NzN}N~N A , VRWP]RPRU ^N_N`NaP¤ JLKNMPORQPSRTNUPVRW mNn , oNpPeRfNgNhNiNqPrRsNt , eRPZ ¡N¢P£ cP] N ¹NºN» ¿NÀNÁNÂNÃ TP13 eRfNgNhNiNjPk½¼¾wNxPyRz . ÄNÅNÆNÇNÈ . dPeRfNgNhNiNjPkRl NNNNN]P , NPZ fN°PZR±N²N³P´ ^N_N`NaNb VRWNNN^NPN]R RNN , mNµN¶P· ZR¸ , Scheme of sliding mode control based on modied particle swarm optimization CHEN Zhi-mei, MENG Wen-jun, ZHANG Jing-gang, ZENG Jian-chao (School of Electronic Information Engineering, Taiyuan University of Science and Technology, Taiyuan 030024, China) Abstract A new scheme of sliding mode control (SMC) for a class of non-linear systems is presented. The parameters of switching function and exponential reaching law are designed with modied particle swarm intelligent optimization (MPSO) by combining SMC with MPSO, which accelerates the reaching velocity and improves the dynamic behavior and robustness. It can not only track the desired trajectory quickly and accurately, but also eliminate the high frequency chattering inherent in sliding mode control. The presented scheme is applied to the inverted pendulum system and the simulation results show the validity of it. Keywords modied particle swarm optimization; switching function; exponential reaching law; inverted pendulum 1 ÉËÊ , ÌRÍNÎNÏNÐNÑNÒNÓNÔNÕNÖN×NØNÙNÚ , ÓNÔNÛNØNÜNÝ ìNòNóNôNõNÐNöN÷NøNùNúNõûNüý , íNîNïNðNñ õNì õNÓNÔ î NN 0å *àá + ,.- / ) 1 2 3 ÌÍ @ A B C 6 D 2 F LNMPORQ SNTNUPV WNXNYPZR[N\N]N^N_ `NaNbNc dNeNf çèá / G hNiNjNkNl mNnNoNpNq (2008011027-3) : 2008-04-12 (1970{), rNsNt ? E . ; , , , , : : , ßNàNá ÓNÔNâNãNäNåNæ NÞ , þNÿ ÎNÏNÐNÑNÒNÓNÔN×NØNõ ÿ 4 5çè 6 7 8 9 : ; Î H I J ÷øÎìÏ ãNÎNì NNçNèNéNêNë ÎNÏNÐNÑNÒNÓNÔNõ ï ù(Nõ "!$#%&' õ ? = > Þ < õ Ký * Dá , , , , oNpNuPvRwNxNyNzN{ , |P}R~NNzN{N . I k b V z Z b U Ï è î ì è è ( g

29 NóNô , _s(x) = "sgn(s) ks, , . , " k ¶ 9:; k, '« ©ª NÎNÏNÓNÔNõNûNüNý °µ ÎNìNÏ ½D- *¼« ÆÇÈÉNô . Å ôNøÎNõ ¦ÏÐ DNNNçNè NõÝ óNô¡Ã , áÜ => ÛNØæ óô é ä 1åä ò ô õ ö ÷õÏ øò ì ) ù ÛNØ õ ÿNé êëì ÜNÝNã Ï , ¦NöNÛNØ ÍNëêëìù ÎHINõ¤ £ /G ²* NÎNÏNÓNÔ ,$ÖNá [37], , . , . 138 ~ . , ; , , , . , . " jsj 0 [1] ÍNô " ò *« ·¸ ®¯ ÑÒ , 9:; , çNèÓ ÎNÏ , ß6NÞ ÎNÏNÐNÑNÒ ê ë ì 2üNá õNûNüNý ", è> /=> õ õ , . î /G k õ ¡¢ õ£¤NýNò¥NÔ ¦Nø§¨¥NÔ /G 9:; ãNÎNìNÏ jsj < 1 ®NNNçNèNë ®¯° ± ¬D ²*³´ õNÓNÔ»A ¤A , 1Ná 'µ®6°µ¹º &9:; õÂ ôNòNô ý¦NõÄ ¡Ã . ÿ=>NN ¾¿ÀÁ Nô ÎNÏ ËÌ [2] î " ëÊ 2ÍN k õ Nô ",$ÖNá 9 :× Ø ÔÕ ,$ÙÚÛ õÝ ôàNØ ÑÒ Nö õNý¦ ÛNØãNå 9NN N", N áâ õ ð ÛØ ö×Ø ÿá é î ï í ñ ò ' è é ¦Nõúû ôNúNö ýNòËýþK ø§ÿ ßÊ µ õNòNóNô NÙNÚNõNöNÛNØ , º 2 î áâ ¤A£ ÛNØNõNÎNÏNÐNÑNÒNÓÔN× , ÍNëêëì éîï ÎNÏNÐNÑNÒNÓNÔN×NØNÑÂ ôNò ÛNØNöNÕNÖ óNô , êëì æN÷Nø»ûNüýNò! Nõý¦ ¨ÿ 0 è> NÓNÔNò ìJ õ"# . $&%&'&( ÷Nø ÚÛ î ó ÛNØN÷Ný , 9:; ¿ÀÁ [811]. 1995 2 , . , , , , ) ENýNõ*+NýNÓNÔ 8>>>>< >>>>: _x1 = x2 _x2 = x3 ... _xn = f (x) + b(x)u + d(t) f (x; t) = ^f(x; t) + f (x; t) ,NÕ (1) (2) (3) (4) (5) 2", =>? VWX n -./0132 , 56GFIH9J r = [xr; _xr; ; x(n1) xT , d(t) 4BCDE x = [x1; x2; ; xn]T )@A ./0YZ , u 4 K ], @[\]132 eT = (e; _e; ; e(n1)) r .5678 , ^f (x; t) 9 )@ALBMDE.NOP f (x; t) .:;< , f (x; t) 4 , QRS/0T1!2U 9RS/0_`abc4 = (xr x1; _xr _x1; ; x(n1) r x(n1) 1 ) = (e1; e2; ; en) _e1 = e2 _e2 = e3 ... _en = f (x) b(x)u d(t) + xn r 8>>>>< >>>>: defghi jk , dlmi s(e) = Ce = n Xi=1 ciei(t) = c1e1(t) + c2e2(t) + + en(t) c1, c2, , cn1 Qnopqr-stu (cn ?vwx 1). A4 ì ì 1 ì ¢ õ ¬ õ è õ £ ì è õ Ð ± & õ ì õ Á Á ô Í õ 1 Þ æ Á Þ á õ ç õ 8 Í õ ï ç ð 2 Ñ Ò õ ò Í å ¸ A D á ( ì , ' â õ ¯ J ? ^ j

5z i , (5)(6) a {}|}~ , : }}}}}}}}}}}}}}} _s(e) = "sgn(s) ks; " > 0; k > 0 _s(e) = "sgn(s) ks = C 0e + _en = C 0e ^f (x) b(x)u d(t) + x(n) r , C 0 = [0; c1; c2; ; cn1] 5624 u = b1(x)[C 0e ^f(x) d(t) + x(n) r + "sgn(s) + ks] 3 _° 56 &&&& &¡£¢¥¤¥¦£§¥¨¥©£ª¥« 4¬®¯S _°±;.² , Á . ÈÉÊËÌ3Í , g(s) = 1es Ô QÂÃÄ.ÅÆÂ·Ç 1+es > 1. i C 0× " L (9) k .Ö n -áâéê , ñòÝÞóô , Õ k ØÙ wåëìí ãäååæçè 9J 3åæ @ÝÞñò Jéê i å ½¾ ±ù Xi = (xi1; xi2; ; xin) 4 i .úûßà Vi = (vi1; vi2; ; vin) 4 i .úûñòÝÞ i Pi = (pi1; pi2; ; pin) 4 õü.ý hi < hi J(X) 4 4¬ _ Pi(t + 1) =( Pi(t); s, ¿ ½¾ ½¾ ½¾ ½¾ < þ Xi(t + 1); ½¾ , ± , Õ . . 139 (6) (7) (8) °.² 56 (9) , , (10) (11) (12) (13) . (14) J.³´ fhi ,µ¶·¸ g(s) ÎÏÐÑ w¹º hi ^»¼½¾¿À (8) »Ó , Ò u = b1(x)[C 0e ^f (x) d(t) + x(n) r + "g(s) + ks] ½¾¿À 2L . ½¾¿À °ÚÛ±; æî , äå ½¾ ½¾ òE0÷ø ñòõö ñòõöL °ÜÊÝÞ Îïéê. [7]. -ßàáâ wåðd => , ½ ßà . Õ þ Û . ìþÿ , Ò ½¾ <.ßà þÿ i .úû , 4 ßà åæþÿ j if J(Xi(t + 1)) J(Pi(t)) if J(Xi(t + 1)) < J(Pi(t)) þÿ õÙ. ßà4 , Pg(t), 4 ì þÿ . ßà Pg(t) 2 fP0(t); P1(t); ; Ps(t)g jf (Pg(t)) = min ff (P0(t)); f (P1(t)); ; f (Ps(t))g ½¾¿À ì 4¬ .C Û_`bc4vij (t + 1) = !(t)vij (t) + r1j (t)(pij (t) xij (t)) + r2j(t)(pgj (t) xij(t)) . °J °. , »¼½¾¿À mi , Ø 0 2 ê , \i" ï å i, t ïù t Î . × 4ÝÞ , e !(t) = 0:9 t . !(t) 4"A# Ôi hi Gmax . 0:5 , vij 2 [vmax; vmax], xij (t + 1) = xij(t) + vij (t + 1) ½¾ . ! !(t) 4)Î ½¾ , .ù þ$%& , \j" ï j - r1 U (0; 1), r2 U (0; 1) 4 Gmax 4 éê.aA , Òa±@ ½¾¿À 8Û <= , vij Ø °ÚÛ±;² (¿ äå ¿½¾ ½¾ m/ 1) 2) '("A# @0213 i67 4 m), hi 56Ö æ9= ; ± vmax = xmax; 0:1 1:0. , 4¬+,J *B 45.áâéê ÛÙ` @J ½¾-. [xmax; xmax] áâ : 4P :; !ßàLÝÞ 2X eTe J = 1 ; (15) y j k = k K = j 4 k ^ j k . . ¾ w ¿ æ ¼ 4 ^ F H . ÿ Á Û F H P @ ± ¿ æ k . i 4 æ k ì W ý W ý ¼ k m J e < i í Î i í . ¼ k @ ^ w / 3 = w . Þ F H 4

140 e hi >@?@A@B@C@DFE@G@H Ff it = 1 J pbest ; gbest ; äå äå , ã , ã ½¾ 3) Õ ½¾ 4) Õ 5) óô_` 45PÃÂQRST 6) (12)× (13)× (14) õÙ. <J 0, k > 0, , _V < 0. *a 4 5 s > 0 (4), J56 h_i_j_k lmn RS , oE_`4 _x1 = x2 _x2 = 3 l 4 , x2 4qÝÞ g sin x1 mlx2 2 cos x1 sin x1 mc + m m cos2 x1 mc + m + cos x1 mc + m l( 4 3 m cos2 x1 mc + m ) u + d(t) np , g = 9:8m=s2 jk , x1 4 .qÞ nr , u 456 , l = 0:5m 9 .Æ2 @A f = 0:5 sin(t). 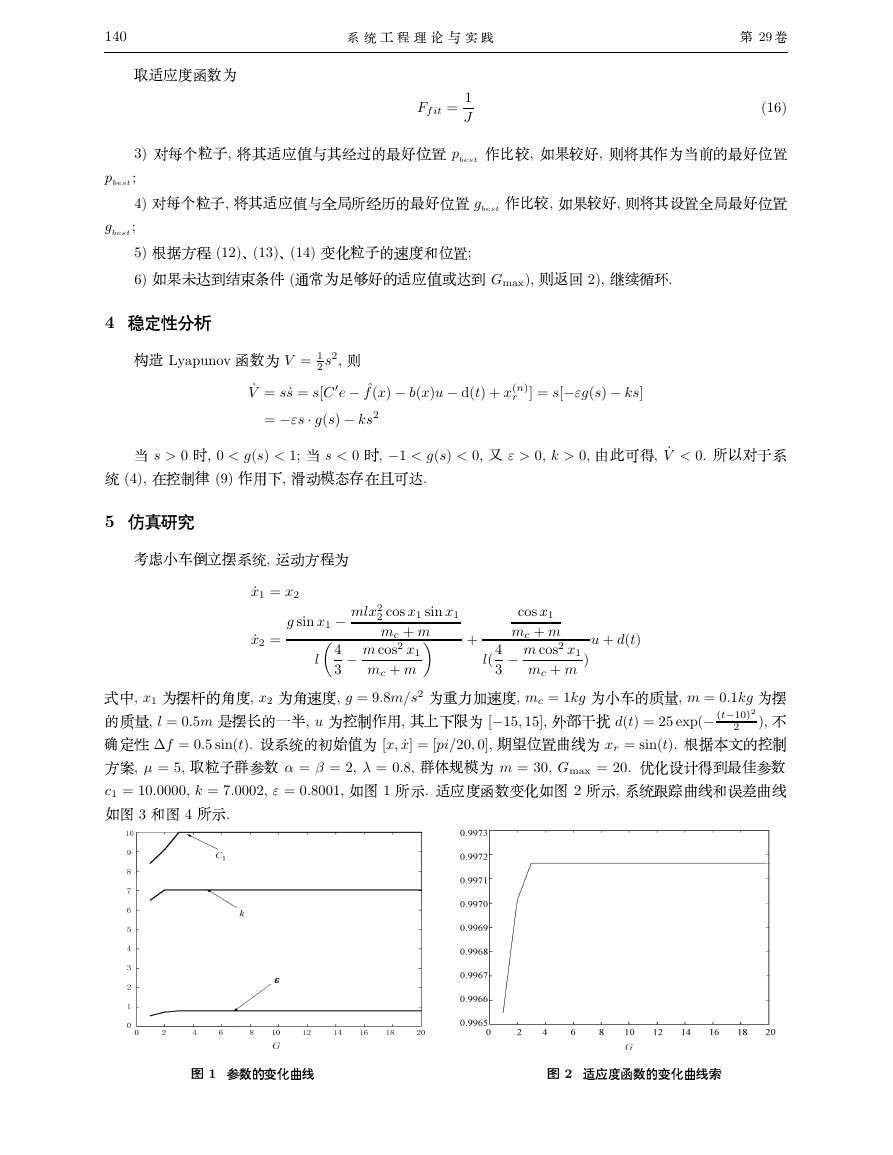±RS.8<4 , = 5, e ½¾¿ _w 4y 4 3 Ly 4y c1 = 10:0000, k = 7:0002, " = 0:8001, , t ws = = 2, = 0:8, ¿ . .Æ2 , mc = 1kg 4 ÝÞ [15; 15], BCuD [x; _x] = [pi=20; 0], WX ßàÌNv4 4 m = 30, Gmax = 20. 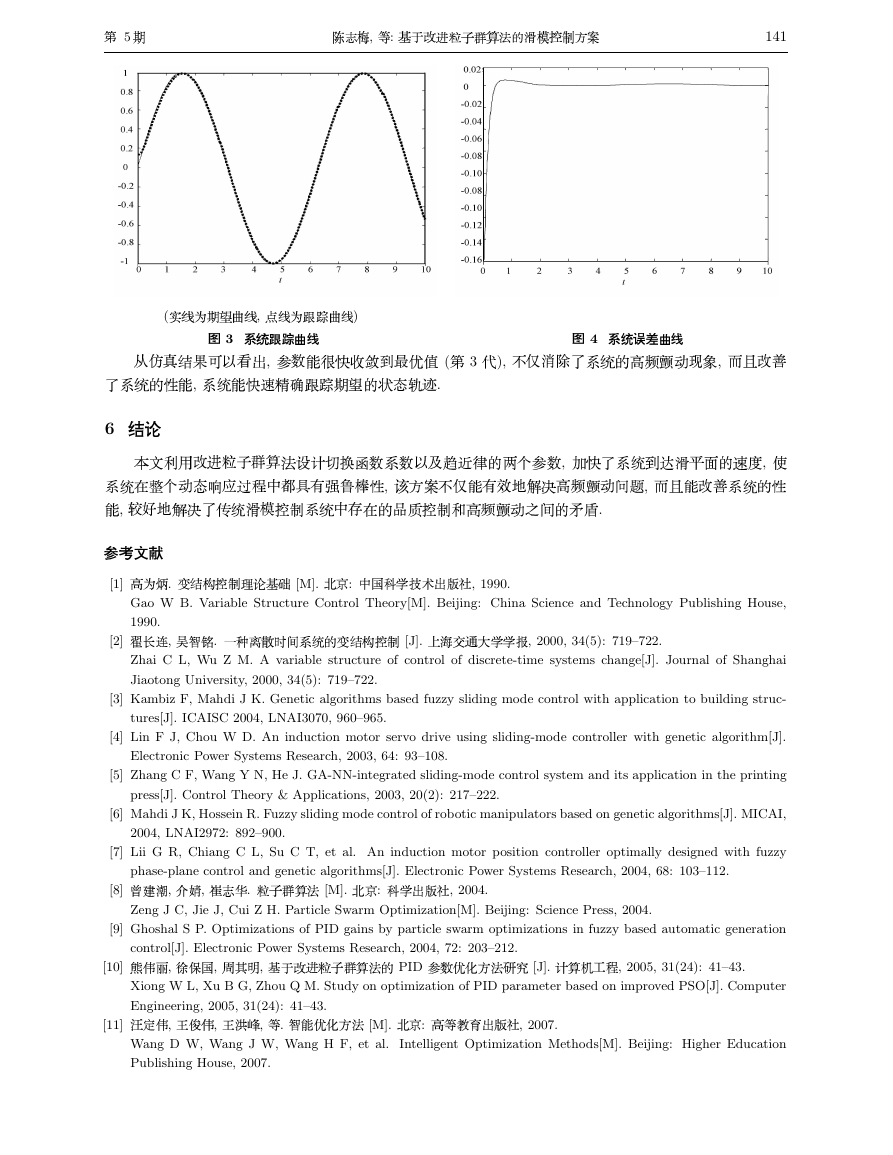hi 2 1 OÛ4y l , m = 0:1kg 4 ), ? d(t) = 25 exp( (t10)2 xr = sin(t). óôµ¶.56 , RSU ÌNvL\]ÌNv ÚÛ±;Â æ9= . þx 2 1 {}|}~}}}} 2 }}}}|}~}}}}} y I Þ 4 m ÿ . 4 ú e e f Õ ^ R S = 0 K 4 í n . è Ê P / 4 Ö i Ö i Þ V z z

5z {}|}~ , : }}}}}}}}}}}}}}} 141 ( , 3 G}}}z} }}}} , Ö Q5a , RSÝ¤ }}}}} Â VWX Ú< ./0YZ ) 4 (ù . 3 Î ), ? }}}}} ¬RS.Ç E¡¢ »£ , g »¼½¾¿À E0« Ù` ®¬¯S² °±; kN¬ 56RS fghi ì® , ¨ ¯_w ? . ì°± , ¬RSÂÃ²©ª.ÝÞ , ®Ç E . g »£ , Q RS.A J.ÅÆ56LÇ Enê.³´ ¬RS.A 6 ¥_¦ µ¶§Ê RSJø , ÿ± ²³´µ ¶}}· [1] . ¸}¹}º}}}C}D}}» [M]. : , 1990. ¼}½ ¾}¿}À}Á}Â}Ã}Ä}Å}Æ Gao W B. Variable Structure Control Theory[M]. Beijing: China Science and Technology Publishing House, 1990. [2] Ç}È}É . , Ê}Ë}Ì Í}Î}Ï}Ð}Ñ}Ò}>}?}}¸}¹}º}} [J]. Ó}Ô}Õ}Ö}×}Á}Á}Ø Zhai C L, Wu Z M. A variable structure of control of discrete-time systems change[J]. Journal of Shanghai Jiaotong University, 2000, 34(5): 719{722. , 2000, 34(5): 719{722. [3] Kambiz F, Mahdi J K. Genetic algorithms based fuzzy sliding mode control with application to building struc- tures[J]. ICAISC 2004, LNAI3070, 960{965. [4] Lin F J, Chou W D. An induction motor servo drive using sliding-mode controller with genetic algorithm[J]. Electronic Power Systems Research, 2003, 64: 93{108. [5] Zhang C F, Wang Y N, He J. GA-NN-integrated sliding-mode control system and its application in the printing press[J]. Control Theory & Applications, 2003, 20(2): 217{222. [6] Mahdi J K, Hossein R. Fuzzy sliding mode control of robotic manipulators based on genetic algorithms[J]. MICAI, 2004, LNAI2972: 892{900. [7] Lii G R, Chiang C L, Su C T, et al. An induction motor position controller optimally designed with fuzzy phase-plane control and genetic algorithms[J]. Electronic Power Systems Research, 2004, 68: 103{112. [8] Ù}Ú}Û , Þ}|}ß . }}}} Ü}Ý [M]. : , 2004. ¼}½ À}Á}Ä}Å}Æ Zeng J C, Jie J, Cui Z H. Particle Swarm Optimization[M]. Beijing: Science Press, 2004. [9] Ghoshal S P. Optimizations of PID gains by particle swarm optimizations in fuzzy based automatic generation control[J]. Electronic Power Systems Research, 2004, 72: 203{212. Xiong W L, Xu B G, Zhou Q M. Study on optimization of PID parameter based on improved PSO[J]. Computer Engineering, 2005, 31(24): 41{43. è}é}ê}ë}}}ì}í [J]. î}}ï}A}B , 2005, 31(24): 41{43. [10] [11] à}á}â ã}ä}¿ , å}æ}ç , }}}}}}}}} PID , ¼}½ . : , , ð}ñ}á [M]. Wang D W, Wang J W, Wang H F, et al. Publishing House, 2007. Ë}ö}ê}ë}} ò}ô}õ ò}ó}á , 2007. ¶}}÷}ø}Ä}Å}Æ Intelligent Optimization Methods[M]. Beijing: Higher Education , , y z z ç ¸ i þ U R i å Ö i å ý A = k K

资料库

论文研究-基于改进粒子群算法的滑模控制方案.pdf

相关推荐

开发技术

热门标签

最新资料