各种RLS算法代码.pdf-资料库

各种最小二乘算法总结盛晓婷 0908110618

盛晓婷最小二乘算法总结报告目录 1. 一般最小二乘法 ...............................................................................3 1.1. 一次计算最小二乘算法 .............................................................3 1.2. 递推最小二乘算法 .....................................................................3 2. 遗忘因子最小二乘算法 ...................................................................6 2.1. 一次计算法 .................................................................................6 2.2. 递推算法......................................................................................6 3. 限定记忆最小二乘递推算法 ...........................................................9 4. 偏差补偿最小二乘法 .....................................................................11 5. 增广最小二乘法 .............................................................................13 6. 广义最小二乘法 .............................................................................15 7. 辅助变量法 .....................................................................................17 8. 二步法 .............................................................................................19 9. 多级最小二乘法 .............................................................................21 10. Yule-Walker辨识算法 .....................................................................23 Matlab程序附录 .......................................................................................24 附录 1、最小二乘一次计算法 ...............................................................24 附录 2、最小二乘递推算法 ...................................................................25 附录 3、遗忘因子最小二乘一次计算法 ...............................................26 附录 4、遗忘因子最小二乘递推算法 ...................................................27 附录 5、限定记忆最小二乘递推算法 ...................................................29 附录 6、偏差补偿最小二乘递推算法 ...................................................31 附录 7、增广最小二乘递推算法 ...........................................................32 1

盛晓婷最小二乘算法总结报告附录 8、广义最小二乘递推算法 ...........................................................34 附录 9、辅助变量法 ...............................................................................36 附录 10、二步法......................................................................................38 附录 11、多级最小二乘法......................................................................39 附录 12、Yule-Walker辨识算法 .............................................................42 图 1 一般最小二乘参数过渡过程 .....................................................4 图 2 一般最小二乘方差变化过程 ....................................................5 图 3 遗忘因子法参数过渡过程 ........................................................7 图 4 遗忘因子法方差变化过程 ........................................................8 图 5 限定记忆法参数过渡过程 ......................................................10 图 6 限定记忆法方差变化过程 ......................................................10 图 7 偏差补偿最小二乘参数过渡过程 ..........................................12 图 8 偏差补偿最小二乘方差变化过程 ..........................................12 图 9 增广最小二乘辨识模型 ..........................................................13 图 10 增广最小二乘参数过渡过程 ................................................14 图 11 广义最小二乘参数过渡过程 ................................................16 图 12 广义最小二乘方差变化过程 ................................................16 图 13 辅助变量法参数过渡过程 ....................................................18 图 14 辅助变量法方差变化过程 ....................................................18 图 15 二步法参数过渡过程 ............................................................20 图 16 二步法方差变化过程 ............................................................20 2

盛晓婷最小二乘算法总结报告 1. 一般最小二乘法例 1 考虑如下仿真对象 z k ( + z k 2) 1.5 ( − z k 1) 0.7 ( ) + + = u k ( u k 1) 0.5 ( ) + + + v k ( ) 其中， v k ( ) 为服从 N (0,1) 分布的白噪声。输入信号 ( )u k 采用 M 序列，幅度为 1。M 序列由 9 级移位寄存器产生， x i = x i − 4 ⊕ 。 x i 9 − 选择如下的辨识模型 z k 1) ( + − = − a z k ( 1 2) + a z k ( ) 2 + b u k ( 1 1) + + b u k ( ) 2 + v k ( ) 观测数据长度取 L = 400 。加权阵取 IΛ = 。 1.1. 一次计算最小二乘算法 ^ θ LS = ⎛ ⎜ ⎜ ⎜ ⎜ ⎜ ⎜ ⎜ ⎝ 2 ^ a 1 ^ a ^ b 1 ^ b 2 ⎞ ⎟ ⎟ ⎟ ⎟ ⎟ ⎟ ⎟ ⎠ = ( H H T L L 1 − ) H Z T L L = -1.4916 0.7005 1.0364 0.4268 ⎛ ⎜ ⎜ ⎜ ⎜ ⎝ ⎞ ⎟ ⎟ ⎟ ⎟ ⎠ (1.1) 其中， Z L = Z Z ... Z ⎛ ⎜ ⎜ ⎜ ⎜ ⎝ (3) (4) (402) ⎞ ⎟ ⎟ ⎟ ⎟ ⎠ ， H L = ⎛ ⎜ ⎜ ⎜ ⎜ ⎜ ⎝ Matlab程序见附录 1。 T T h h ... h T (3) (4) (402) ⎞ ⎟ ⎟ ⎟ ⎟ ⎟ ⎠ = Z − Z − ... Z − ⎛ ⎜ ⎜ ⎜ ⎜ ⎝ (1) (2) (2) (3) Z − Z − ... (401) ... (400) Z − u (2) u (3) ... (401) u u (1) u (2) u (400) ⎞ ⎟ ⎟ ⎟ ⎟ ⎠ 1.2. 递推最小二乘算法递推最小二乘算法公式： ^ ^ ( θ θ k ( ) = k 1) − + K k z k ( )[ ( ) − h k ( ) ' ^ ( θ k − K k ( ) = P k ( − 1) ( )[ h k h k P k ( ( ) ' − h k 1) ( ) + 1)] 1 k ( ) Λ ] 1− (1.2) P k ( ) = [ I K k h k P k ( )] ( − ( ) ' − 1) 3

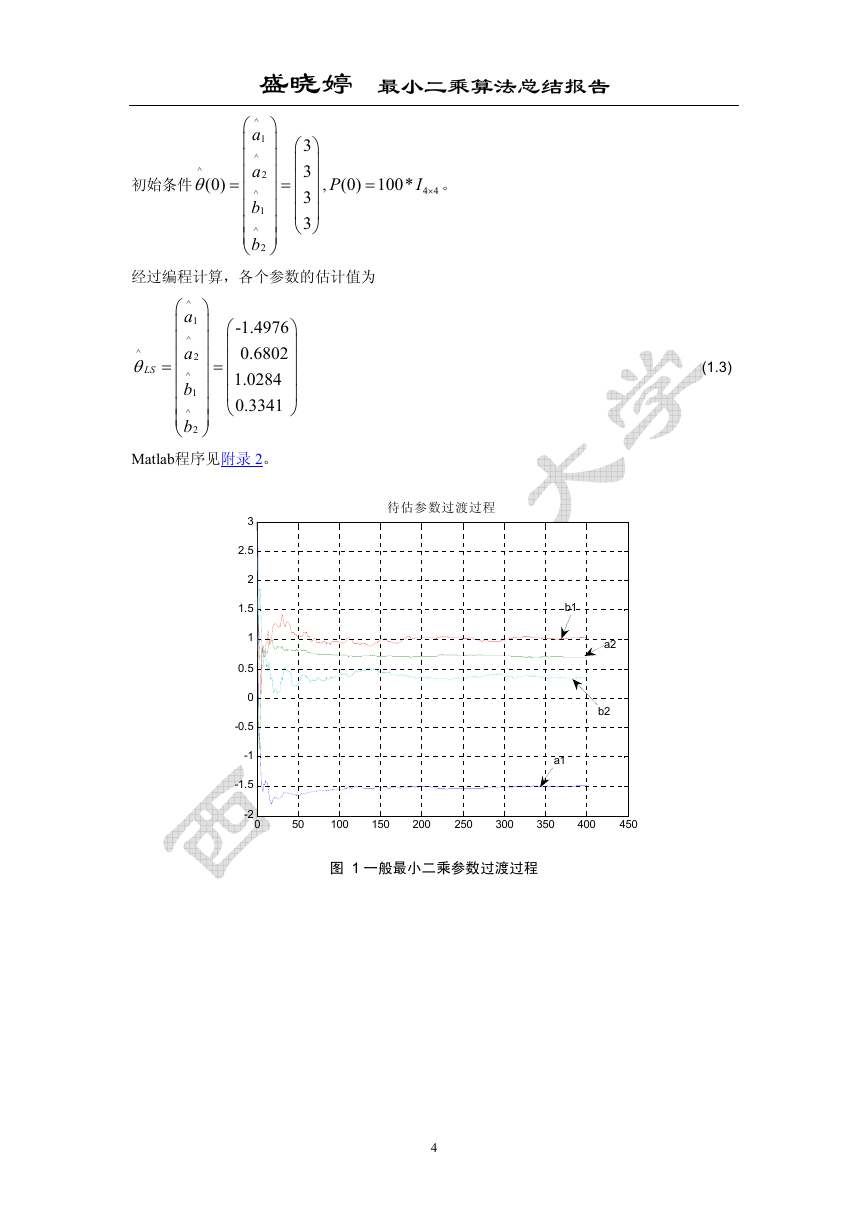
盛晓婷最小二乘算法总结报告 ⎞ ⎟ ⎟ ⎟ ⎟ ⎟ ⎟ ⎟ ⎠ 3 ⎛ ⎞ ⎜ ⎟ 3 ⎜ ⎟ 3 ⎜ ⎟ ⎜ ⎟ 3 ⎝ ⎠ ^ a 1 ^ a ^ b 1 ^ b (0) 100* = I × 4 4 。 , P = 2 2 初始条件 ^ θ (0) = ⎛ ⎜ ⎜ ⎜ ⎜ ⎜ ⎜ ⎜ ⎝ 经过编程计算，各个参数的估计值为 ^ θ LS = ⎛ ⎜ ⎜ ⎜ ⎜ ⎜ ⎜ ⎜ ⎝ 2 ^ a 1 ^ a ^ b 1 ^ b 2 ⎞ ⎟ ⎟ ⎟ ⎟ ⎟ ⎟ ⎟ ⎠ = -1.4976 0.6802 1.0284 0.3341 ⎛ ⎜ ⎜ ⎜ ⎜ ⎝ ⎞ ⎟ ⎟ ⎟ ⎟ ⎠ (1.3) Matlab程序见附录 2。 3 2.5 2 1.5 1 0.5 0 -0.5 -1 -1.5 -2 0 待估参数过渡过程 b1 a1 a2 b2 50 100 150 200 250 300 350 400 450 图 1 一般最小二乘参数过渡过程 4

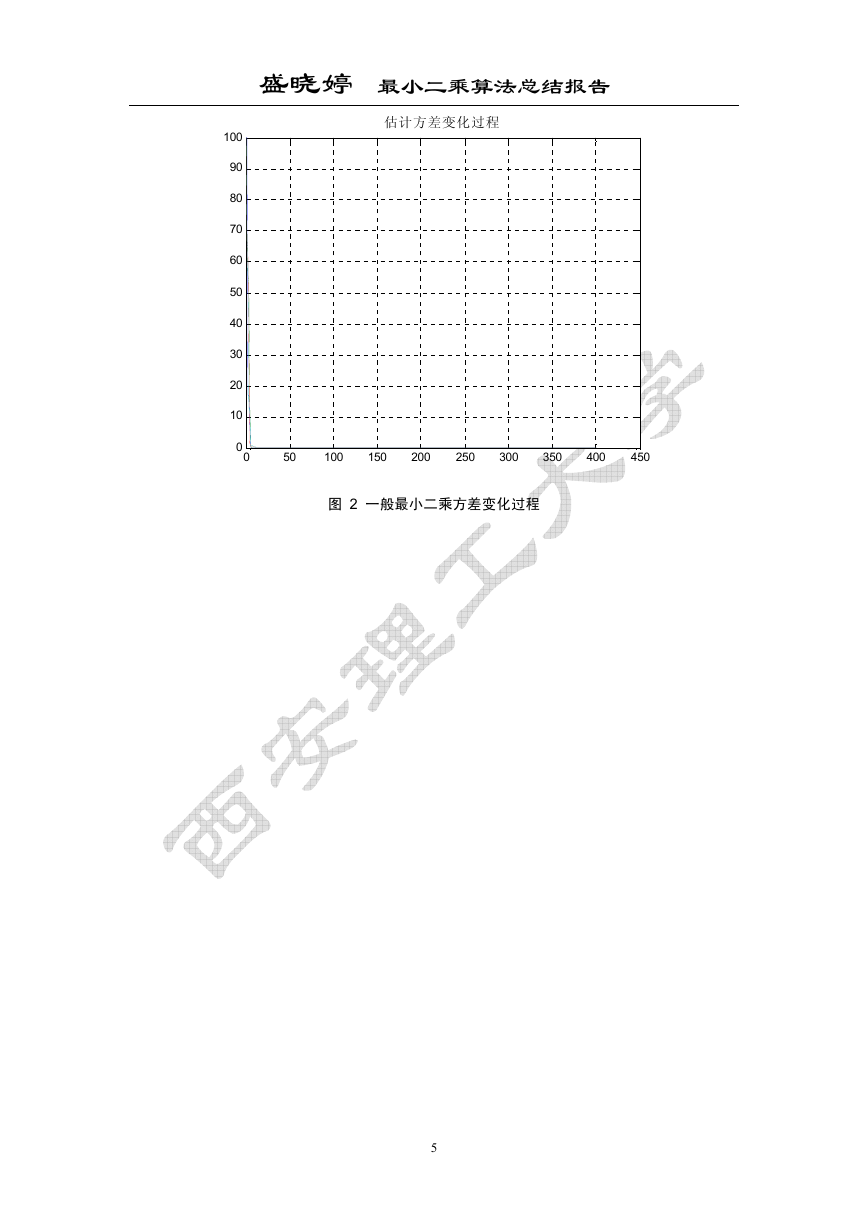
盛晓婷最小二乘算法总结报告估计方差变化过程 50 100 150 200 250 300 350 400 450 图 2 一般最小二乘方差变化过程 5 100 90 80 70 60 50 40 30 20 10 0 0

盛晓婷最小二乘算法总结报告 2. 遗忘因子最小二乘算法采用的辨识模型与例 1相同。 2.1. 一次计算法 2 ^ a 1 ^ a ^ b 1 ^ b 2 ⎛ ⎜ ⎜ ⎜ ⎜ ⎜ ⎜ ⎜ ⎝ ^ θ LS = ⎞ ⎟ ⎟ ⎟ ⎟ ⎟ ⎟ ⎟ ⎠ = ( H H T * L * L ) 1 − H Z T * L * L = ⎛ ⎜ ⎜ ⎜ ⎜ ⎝ -1.4990 0.7060 0.8260 0.4919 ⎞ ⎟ ⎟ ⎟ ⎟ ⎠ (2.1) 1 − − 2 Z * (3) Z * (4) 其中， Z * L ⎛ ⎜ ⎜ = ⎜ ⎜ ⎜ ⎝ L β L β ... Z (402) ， ⎞ ⎟ ⎟ ⎟ ⎟ ⎟ ⎠ H L = ⎛ ⎜ ⎜ ⎜ ⎜ ⎜ ⎝ L β L β ... h T T 1 − − 2 * * h h T (402) (3) (4) ⎞ ⎟ ⎟ ⎟ ⎟ ⎟ ⎠ = ⎛ ⎜ ⎜ ⎜ ⎜ ⎜ ⎝ 2 − 1 − L β − L β − ... Z − Z * (2) Z * (3) ... (401) 2 − 1 − Z * (1) Z * (2) ... L β − L β − ... Z (400) − 1 − L β L β − u * (2) u * (3) 2 1 − L β L β − u * (1) u * (2) 2 u (401) u (400) ⎞ ⎟ ⎟ ⎟ ⎟ ⎟ ⎠ 衰减因子 β= 0.98 ，数据长度 L = 402 。 Matlab程序见附录 3。 2.2. 递推算法遗忘因子递推最小二乘算法公式： ^ ^ k k ( ( ) = θ θ K k P k ( ) ( = 1 [ µ P k ( ) = 1) − + 1) ( )[ − K k z k ( )[ ( ) − h k h k P k ( ( ) ' ^ h k k ( ) ( ' θ h k 1) ( ) − I K k h k P k ( )] ( − ( ) ' − 1) (2.2) − + 1)] ] 1µ − 6

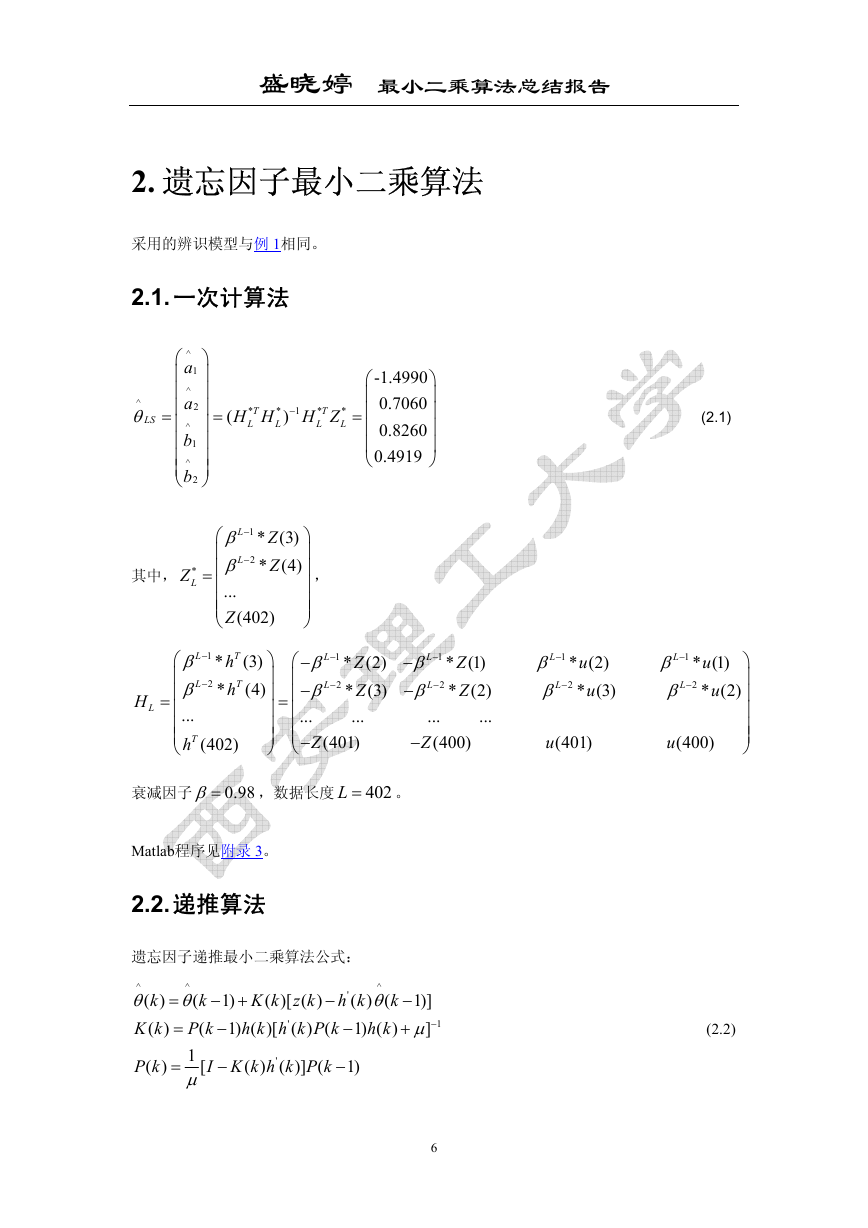
盛晓婷最小二乘算法总结报告其中，0 µ≤ 1 ≤ 为遗忘因子，此处取 0.98。数据长度 L=402，初始条件 ^ θ (0) = ⎛ ⎜ ⎜ ⎜ ⎜ ⎜ ⎜ ⎜ ⎝ 2 ^ a 1 ^ a ^ b 1 ^ b 2 ⎞ ⎟ ⎟ ⎟ ⎟ ⎟ ⎟ ⎟ ⎠ = ⎛ ⎜ ⎜ ⎜ ⎜ ⎝ 0.001 0.001 0.001 0.001 ⎞ ⎟ ⎟ ⎟ ⎟ ⎠ , P (0) 10* = I × 4 4 。经过编程计算，各个参数的估计值为 ^ θ LS = ⎛ ⎜ ⎜ ⎜ ⎜ ⎜ ⎜ ⎜ ⎝ 2 ^ a 1 ^ a ^ b 1 ^ b 2 ⎞ ⎟ ⎟ ⎟ ⎟ ⎟ ⎟ ⎟ ⎠ = -1.4852 0.6720 1.0734 0.4387 ⎛ ⎜ ⎜ ⎜ ⎜ ⎝ ⎞ ⎟ ⎟ ⎟ ⎟ ⎠ (2.3) Matlab程序见附录 4。 2 1.5 1 0.5 0 -0.5 -1 -1.5 -2 0 待估参数过渡过程 b1 a2 b2 a1 50 100 150 200 250 300 350 400 450 图 3 遗忘因子法参数过渡过程 7

资料库

各种RLS算法代码.pdf

相关推荐

行业

热门标签

最新资料