2009年西北工大校车安排问题论文.doc-资料库

jingzhixingyun-3045409-16359647532160077902.doc.pdf-第1页.png

第1页 / 共22页

jingzhixingyun-3045409-16359647532160077902.doc.pdf-第2页.png

第2页 / 共22页

jingzhixingyun-3045409-16359647532160077902.doc.pdf-第3页.png

第3页 / 共22页

jingzhixingyun-3045409-16359647532160077902.doc.pdf-第4页.png

第4页 / 共22页

jingzhixingyun-3045409-16359647532160077902.doc.pdf-第5页.png

第5页 / 共22页

jingzhixingyun-3045409-16359647532160077902.doc.pdf-第6页.png

第6页 / 共22页

jingzhixingyun-3045409-16359647532160077902.doc.pdf-第7页.png

第7页 / 共22页

jingzhixingyun-3045409-16359647532160077902.doc.pdf-第8页.png

第8页 / 共22页

第 1 页共 22 页一、问题重述许多学校都建有新校区，常常需要将老校区的教师和工作人员用校车送到新校区。由于每天到新校区的教师和工作人员很多，往往需要安排许多车辆。根据附录表一、二的数据，合理、有效的设置乘车点，安排车辆。让教师和工作人员尽量满意。问题 1：如要建立n个乘车点，为使各区人员到最近乘车点的距离最小，该将校车乘车点应建立在哪n个点。建立一般模型，并给出 2,3 n  时的结果。问题 2：若考虑每个区的乘车人数，为使教师和工作人员满意度最大，该将校车乘车点应建立在哪n个点。建立一般模型，并给出 2,3 n  时的结果。问题 3：若建立 3 个乘车点，为使教师和工作人员尽量满意，至少需要安排多少辆车？给出每个乘车点的位置和车辆数。设每辆车最多载客 47 人（假定车只在起始站点载人）。问题 4：关于校车安排问题，你还有什么好的建议和考虑。可以提高乘车人员的满意度，又可节省运行成本。二、基本假设 1．假设未给出距离的两个区可以通过其他区间接到达。 2．每位教师及工作人员均选择最短路径乘车。 3．乘车点均建在各区内，不考虑区与区之间。 4. 教师及工作人员到各站点乘车的满意度与到该站点的距离有关系，距离近则满意度高，距离远则满意度低。 5. 假设任意时刻任意站点均有车，不考虑教师及工作人员的等车时间。 6. 在乘车点区内的人员乘车距离为零。 7. 根据实际情况，我们假设所设置的乘车点数不大于 50。 8. 假设所有人员均乘车。三、符号的说明表示意义第 i 个区域 i=1,2,3,...50 第 i 个区域 i=1,2,3,...50 第 i 区与第 j 区的最短距离 i=1,2,3,...50 j=1,2,3,...50 任意两区的最短距离矩阵符号 ni Vi dij D 2009 年西北工大“工大正禾杯”校车安排问题论文作者王景

第 2 页共 22 页表示意义含义是从 Vi 到 Vj 的最短路要经过点号为 rij的点．任意两区最短距离路径矩阵表示 t 区教师和工作人员到最近乘车点的距离表示 t 区的乘车人数，表示 nt 乘车点应安排的车辆数。t=1,2,3 表示 t 区人数 Pt 乘以距离 St 符号 rij R St Pt Bt Wt 四、问题分析许多学校都建有新校区，常常需要将老校区的教师和工作人员用校车送到新校区。由于每天到新校区的教师和工作人员很多，往往需要安排许多车辆。因此有必要合理设置乘车点并安排各站点的车辆数目，以便最大程度上满足教师及工作人员的需要。我们假设教师和工作人员去乘车时都去最近的乘车点。这样，他们走的路程越短，就越满意。在我们设置好乘车点后，每个人走的路程相加所得的和最小时，教师和工作人员乘车的总体满意度就最高。若考虑各区人数的差异，则在前一问题的基础上给路程之和乘以各区人数，所得值越小则满意程度越高。五、模型建立与求解问题一模型的建立及求解：第一步:用 Floyd 算法求出距离矩阵 D=（dij）v×v . 1. 算法的基本思想直接在图的带权邻接矩阵中用插入顶点的方法依次构造出个矩阵 D(1)、 D(2)、… 、D( )，使最后得到的矩阵 D()成为图的距离矩阵，同时也求出 2009 年西北工大“工大正禾杯”校车安排问题论文作者王景

第 3 页共 22 页插入点矩阵以便得到两点间的最短路径． 2.算法原理（1）求距离矩阵的方法把带权邻接矩阵 W 作为距离矩阵的初值， ) 根据题目所给各区距离表列出 D(0)= 即 D(0)= )0( ijd ( ( )0( ijd ) 50×50 距离矩阵 ○1 D(1)= 其中 ( )1( d ij )1( ijd  ， ) min{ d )0( ij , d )0( 1 i 1 jd })0( )1( ijd 是从 Vi 到 Vj 的只允许以 V1 作为中间点的路径中最短路的长度. ○2 D(2)= 其中 ( d )2( ijd )2( ij ， ) min{ d  )1( ij , d )1( 2 i })1( 2 jd )2( ijd 是从 Vi 到 Vj 的只允许以 V1 、 V2 作为中间点的路径中最短路的长度． …………… …………… ○V D(V)= )(  ij 其中 d ( ) (  ijd  ) ，  min{ d ( )1   ij , d ( )1   i  (    jd })1 )( ijd 是从 Vi 到 Vj 的只允许以 V1、V2、…VV 作为中间点的路径中最短路的长度．即是从 Vi 到 Vj 中间可插入任何顶点的路径中最短路的长，因此 D( )即是距离矩阵． (2)求路径矩阵的方法在建立距离矩阵的同时可建立路径矩阵 R，R= ( ijr ) ,rij的含义是 Vi 到 Vj 的最短路要经过点号为 rij的点． )0( R  ( )0( ijr )  , rij )0( j 每求得一个 D(k) 时，按下列方式产生相应的新的 R(k) 2009 年西北工大“工大正禾杯”校车安排问题论文作者王景

第 4 页共 22 页 k )1 k  k )1  d 若 ( ij )1   d ( k kj )1  ( k ik d  否则 )( k r ij    ( r  ij 即当 Vk 被插入任何两点间的最短路径时，被记录在 R(k) 时求得 R(v) ,可由 R(v) (3)查找最短路径的方法来查找任何点对之间最短路的路径．中，依次求 D(v) )( rij  p 1 若，则点p1是点 i到点 j的最短路的中间点. 然后用同样的方法再分头查找．若：（１）向点 i追朔得：（２）向点 j追朔得：则由点 i到 j的最短路的路径为： ) p 3 2 , ,…, ( rip  p 1 )( r jp  q , 1 1 , pi k )( rip  ) ( r k ip 2 )( r jqm j )( r jq  q 1 , , , , , , jq qqpp   2 2 m ,…, 2 , 1,1 p k 3.算法步骤 Floyd 算法：求任意两点间的最短路 D(i,j)：i到 j的距离． R(i,j)：i到 j之间的插入点．输入: 带权邻接矩阵 w(i,j) （１）赋初值：对所有 i,j, d(i,j)w(i,j), r(i,j)j, k1 (2) 更新 d(i,j), r(i,j) 对所有 i,j ，若 d(i,k)+d(k,j)

第 5 页共 22 页 D(50)=（dij）50×50矩阵如下： 1 0 400 450 700 910 1140 1110 2 400 0 850 300 510 740 710 1280 880 3 450 850 0 600 810 1040 1010 1180 1480 1080 1380 4 700 300 600 0 210 440 410 580 780 5 910 510 810 210 0 230 200 370 570 6 7 8 9 …… 48 49 50 1140 1110 1280 1480 …… 1110 1310 1510 740 710 880 1080 …… 710 910 1110 1040 1010 1180 1380 …… 1560 1760 1875 440 230 0 320 340 540 410 200 320 0 170 370 580 370 340 170 0 780 …… 1010 1210 1275 570 …… 1220 1420 1485 540 …… 1450 1650 1620 370 …… 1164 1364 1300 200 …… 1334 1534 1470 200 0 …… 1534 1734 1640 1 2 3 4 5 6 7 8 9 …… …… …… …… …… …… …… …… …… …… …… …… …… …… 48 49 50 1640 …… 1100 1734 …… 200 1534 …… 0 1560 1010 1760 1210 1875 1275 1220 1450 1420 1650 1485 1620 1510 1110 1164 1334 1364 1534 1300 1470 710 910 1100 1300 1110 1310 200 0 1300 0 第二步：设置 n 个乘车点时的取点情况算法思路：我们假设教师和工作人员去乘车时都去最近的乘车点。这样，他们走的路程越短，就越满意。在我们设置好乘车点后，由于不考虑每个区的乘车人数，每个区人员到最近乘车点乘车，乘车所走最短距离相加所得的总和最小时，教师和工作人员乘车的总体满意度就最高。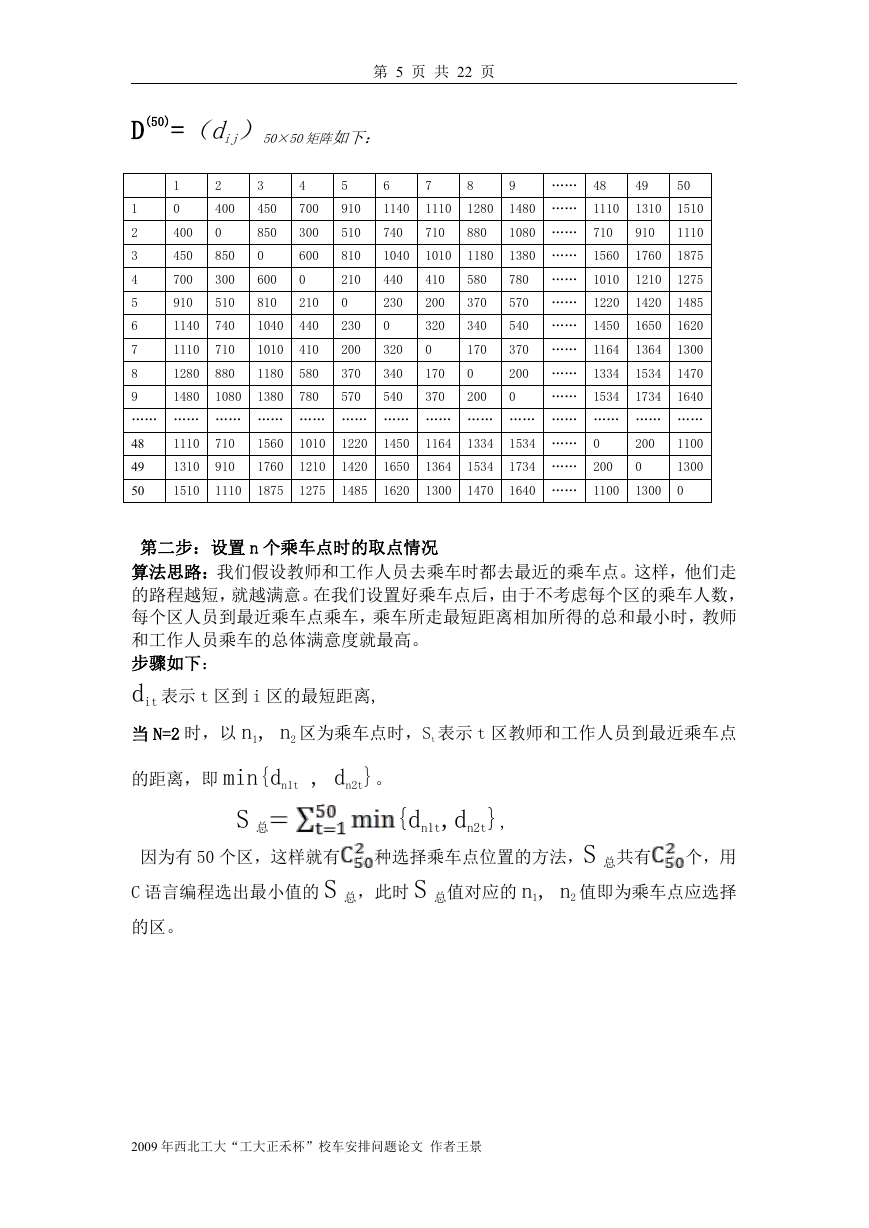步骤如下： dit 表示 t 区到 i 区的最短距离, 当 N=2 时，以 n1, n2 区为乘车点时，St 表示 t 区教师和工作人员到最近乘车点的距离，即 min{dn1t , dn2t}。 S 总 {dn1t,dn2t}, 因为有 50 个区，这样就有种选择乘车点位置的方法，S 总共有个，用 C 语言编程选出最小值的 S 总，此时 S 总值对应的 n1, n2 值即为乘车点应选择的区。 2009 年西北工大“工大正禾杯”校车安排问题论文作者王景

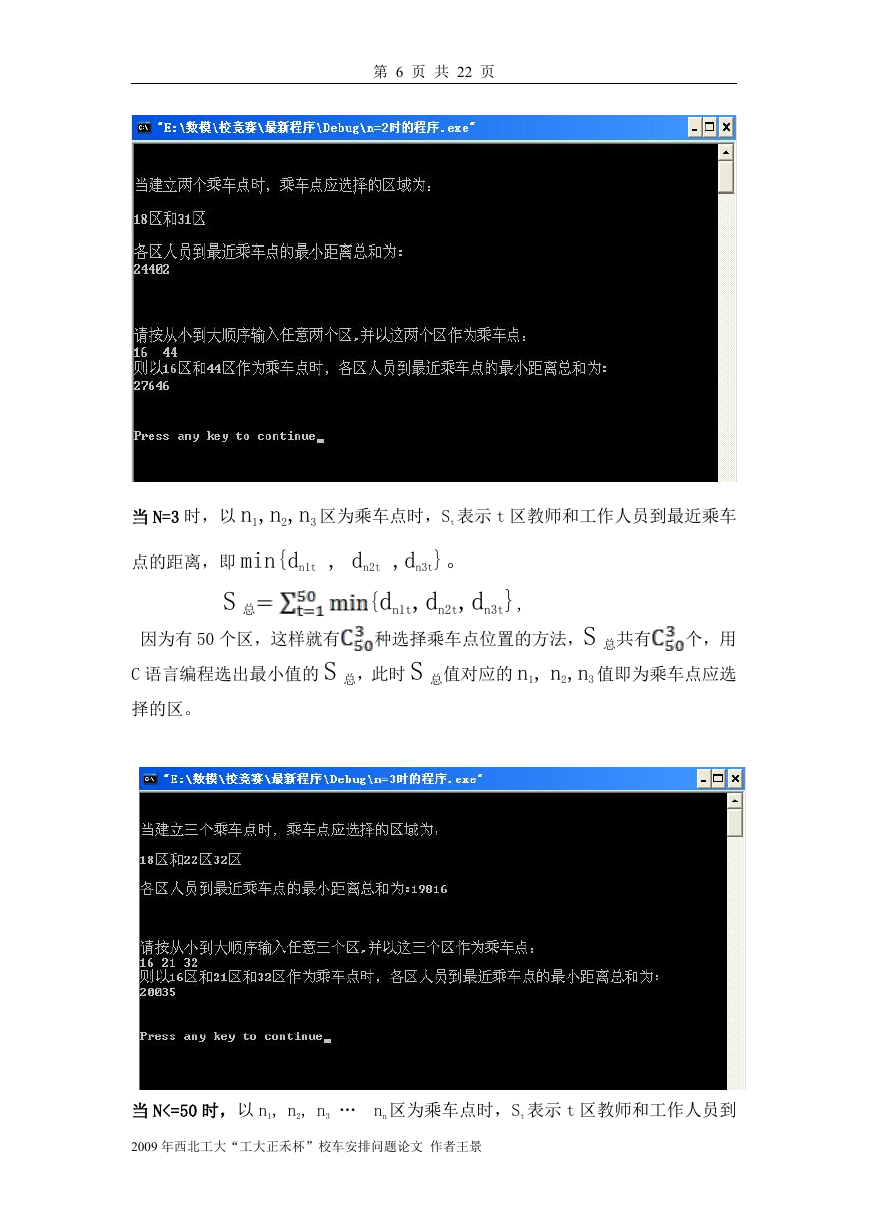
第 6 页共 22 页当 N=3 时，以 n1,n2,n3 区为乘车点时，St 表示 t 区教师和工作人员到最近乘车点的距离，即 min{dn1t , dn2t ,dn3t}。 S 总 {dn1t,dn2t,dn3t}, 因为有 50 个区，这样就有种选择乘车点位置的方法，S 总共有个，用 C 语言编程选出最小值的 S 总，此时 S 总值对应的 n1, n2,n3 值即为乘车点应选择的区。当 N<=50 时，以 n1, n2, n3 … nn 区为乘车点时，St 表示 t 区教师和工作人员到 2009 年西北工大“工大正禾杯”校车安排问题论文作者王景

第 7 页共 22 页最近乘车点的距离，即 min{dn1t , d n2t，dn3t……dnnt}。 S 总= (dit,djt…dpt), 因为有 50 个区，这样就有种选择乘车点位置的方法，S 总共有个，用 C 语言编程选出最小值的 S 总，此时 S 总值对应的 n1, n2,n3 … nn 值即为乘车点应选择的区。问题二模型的建立及求解算法思路：我们假设教师和工作人员去乘车时都去最近的乘车点。这样，他们走的路程越短，就越满意。在我们设置好乘车点后，考虑到每个区的人数不同。这样，每个人到最近乘车点乘车，乘车所走最短距离相加所得的总和最小时，教师和工作人员乘车的总体满意度就最高。步骤如下： Pt 表示 t 区的乘车人数， dij 表示 i 区与 j 区的最短路径值，当 N=2 时，以 n1, n2 区为乘车点时，St 表示 t 区教师和工作人员到最近乘车点的距离，即 min{dn1t , dn2t}。我们以 t 区人数 Pt 乘以距离 S 作为 Wt 值，即 Wt=Pt*St= Pt*min{dn1t , dn2t} W 总= = *St W 总值可作为所有教师和工作人员乘车满意度 H 的衡量标准，即当 W 总越小，满意度 H 越高。W 总越大，满意度 H 越低。因为有 50 个区，这样就有种选择乘车点位置的方法，即有个 W 总值。用 C 语言编程选出最小值的 W 总值，此时 W 总值对应的 n1, n2 值即为乘车点应选择的区。 2009 年西北工大“工大正禾杯”校车安排问题论文作者王景

第 8 页共 22 页当 N=3 时，以 n1,n2,n3 区为乘车点时，St 表示 t 区教师和工作人员到最近乘车点的距离，即 min{dn1t , dn2t ,dn3t}。我们以 t 区人数 Pt 乘以距离 S 作为 Wt 值，即 Wt=Pt*St= Pt*min{dn1t ,dn2t ,dn3t} W 总= = *St W 总值可作为所有教师和工作人员乘车满意度 H 的衡量标准，即当 W 总越小，满意度 H 越高。W 总越大，满意度 H 越低。因为有 50 个区，这样就有种选择乘车点位置的方法，即有个 W 总值。用 C 语言编程选出最小值的 W 总值，此时 W 总值对应的 n1,n2,n3 值即为乘车点应选择的区。 2009 年西北工大“工大正禾杯”校车安排问题论文作者王景

资料库

2009年西北工大校车安排问题论文.doc

相关推荐

课程资源

热门标签

最新资料