圆孔矩孔的菲涅尔衍射模拟(matlab实现).docx

发布时间：2022-06-18 发布人：admin 分类：说明书资料大小：0.24M 资料格式：docx 举报版权申诉

9c57eabf-ee17-4cc0-9bad-589ae5e35a4b.docx.pdf-第1页.png

第1页 / 共7页

9c57eabf-ee17-4cc0-9bad-589ae5e35a4b.docx.pdf-第2页.png

第2页 / 共7页

9c57eabf-ee17-4cc0-9bad-589ae5e35a4b.docx.pdf-第3页.png

第3页 / 共7页

9c57eabf-ee17-4cc0-9bad-589ae5e35a4b.docx.pdf-第4页.png

第4页 / 共7页

9c57eabf-ee17-4cc0-9bad-589ae5e35a4b.docx.pdf-第5页.png

第5页 / 共7页

9c57eabf-ee17-4cc0-9bad-589ae5e35a4b.docx.pdf-第6页.png

第6页 / 共7页

9c57eabf-ee17-4cc0-9bad-589ae5e35a4b.docx.pdf-第7页.png

第7页 / 共7页

文本预览

XX 大学 XXXX 学院工程光学综合练习 -----圆孔、矩孔的菲涅尔衍射模拟 1

XX 大学 XXXX 学院圆孔和矩孔的菲涅尔衍射模拟一、原理由惠更斯-菲涅尔原理可知接收屏上的 P 点的复振幅可以表示为 Kθdσ 完善，有设衍射屏上点的坐标为（x1, y1），接收屏上点的坐标为（x, y），衍射屏与接收屏间距离为 z1，当满足菲涅尔近似条件时，即 (1) 其中Q 为衍射屏上的复振幅分布，K(θ)为倾斜因子。根据基尔霍夫对此公式的 = Q exp C=1 Kθ =1+2 ≈1 813[(−1)2+(−1)2]2 ≪ (2) 此时可得到菲涅尔衍射的计算公式x,y =exp 1 exp 21 −1 2 ∞1,1 iλ1 −∞ + −1 2 11 (3) exp 21 2+2 x,y =exp (1) f1,1 exp 21 12+12 (4) iλ1 x1、y1 无关的振幅和相位因子外，菲涅尔衍射的复振幅分布是孔径平面的复振以及光强分布，考虑到这三个量都是二维分布,而且Matlab 主要应用于矩阵数值运算,所以本程序选择用二维矩阵来存储衍射孔径平面和观察平面的场分布,并分别以矩阵的列数和行数来对应平面的直角坐标值(x,y)以及(x1,y1)。上式为菲涅尔衍射的傅里叶变换表达式，它表明除了积分号前面的一个与幅分布和一个二次相位因子乘积的傅里叶变换。相对于夫琅和费衍射而言，菲涅尔衍射的观察屏距衍射屏不太远。在菲涅尔衍射中，输入变量和输出变量分别为衍射孔径平面的光场分布和观察平面的光场把上式指数项中的二次项展开，并改写成傅里叶变换的形式，可以写成二、圆孔菲涅尔衍射 2

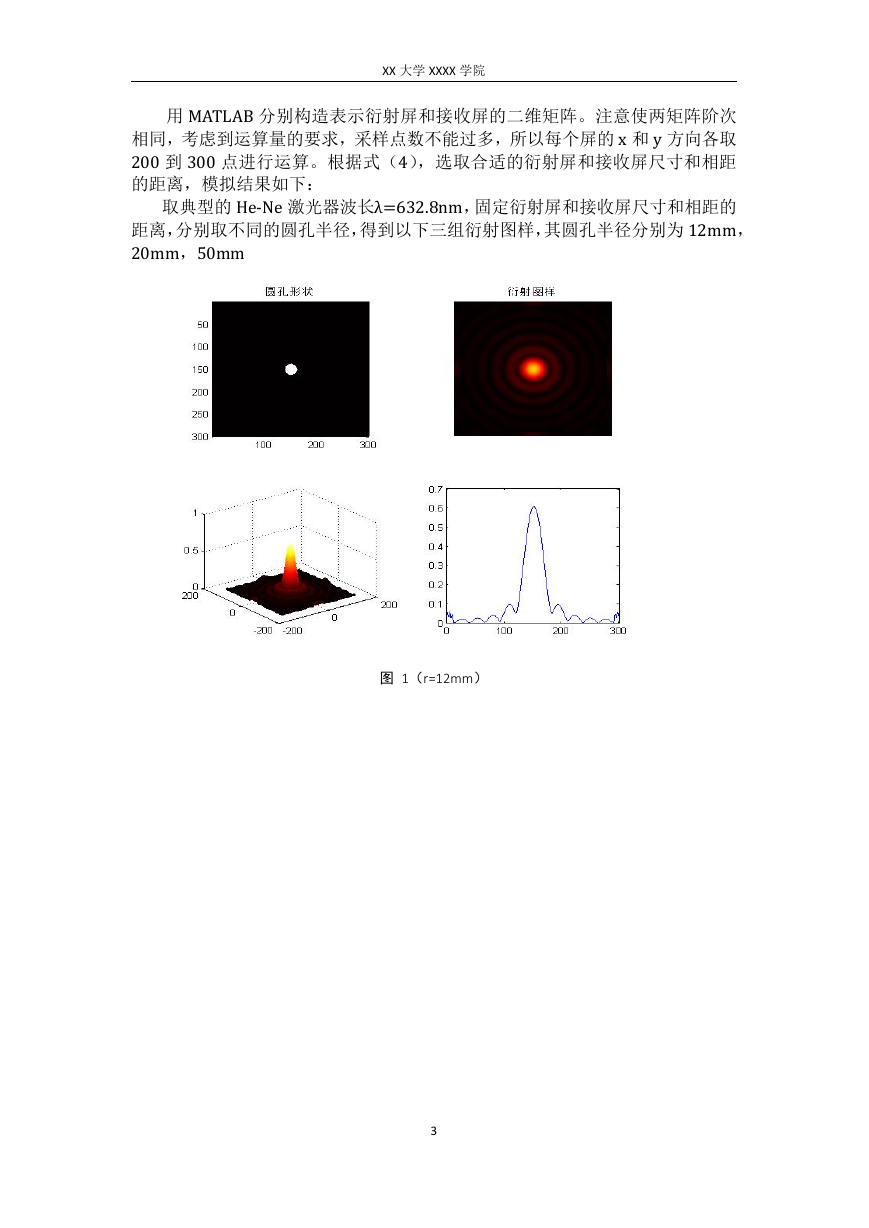
XX 大学 XXXX 学院的距离，模拟结果如下：用MATLAB 分别构造表示衍射屏和接收屏的二维矩阵。注意使两矩阵阶次相同，考虑到运算量的要求，采样点数不能过多，所以每个屏的x 和y 方向各取 200 到300 点进行运算。根据式（4），选取合适的衍射屏和接收屏尺寸和相距取典型的He-Ne 激光器波长λ=632.8nm，固定衍射屏和接收屏尺寸和相距的距离，分别取不同的圆孔半径，得到以下三组衍射图样，其圆孔半径分别为12mm， 20mm，50mm 图 1（r=12mm） 3

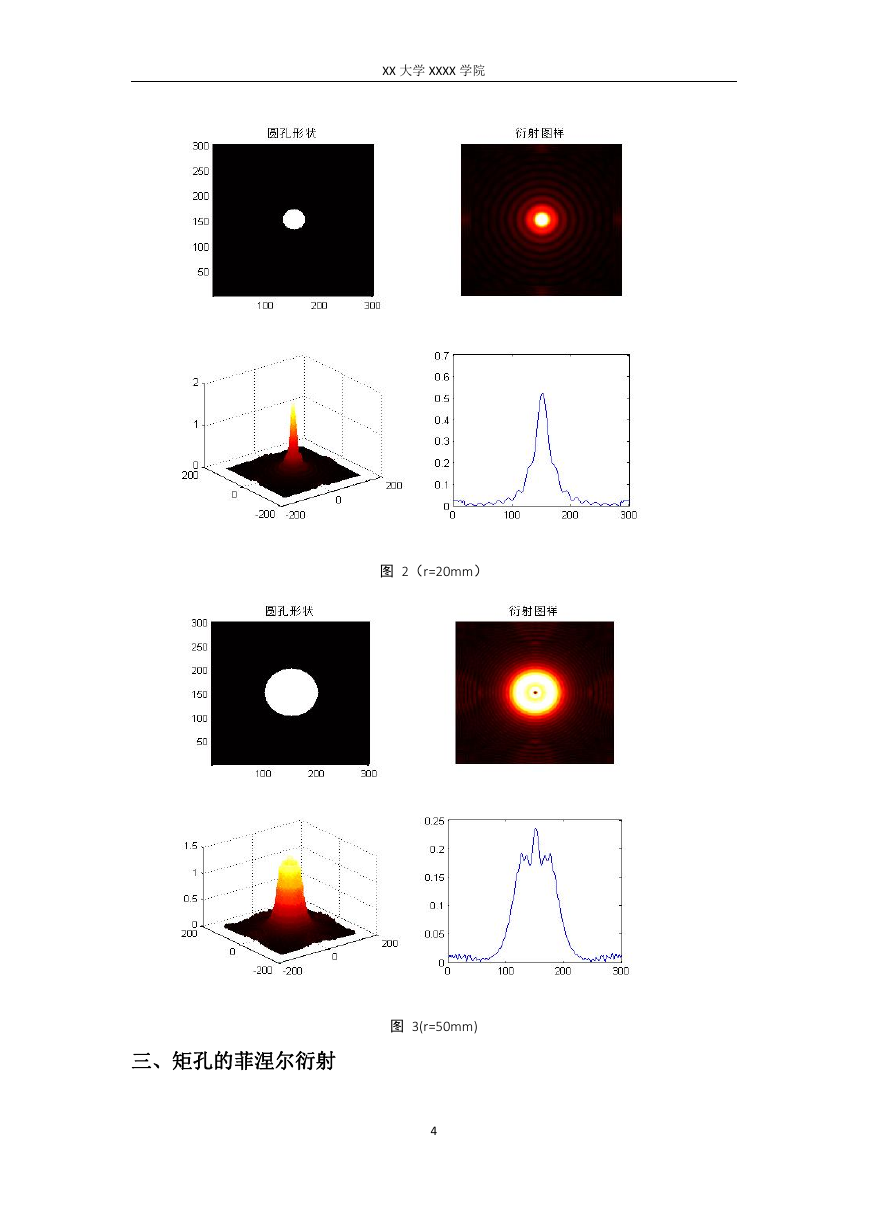
XX 大学 XXXX 学院图 2（r=20mm）三、矩孔的菲涅尔衍射图 3(r=50mm) 4

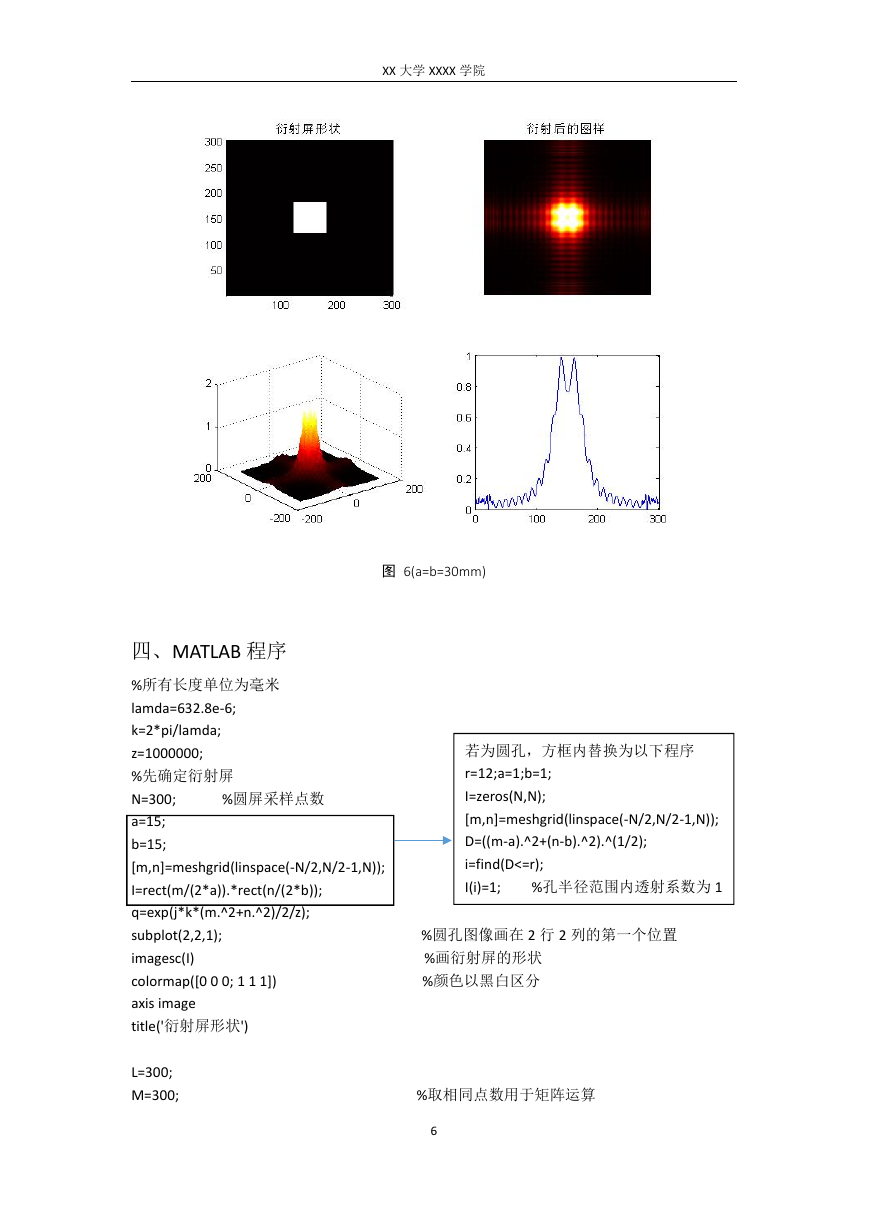
XX 大学 XXXX 学院步骤与上述相同，仅需改变与衍射屏形状对应的矩阵。这里选择矩孔的长宽相等，分别为 15mm，20mm，30mm，其衍射图样及强度分布如图 4、5、6 图 4（a=b=15mm）图 5(a=b=20mm) 5

XX 大学 XXXX 学院图 6(a=b=30mm) %圆屏采样点数四、MATLAB 程序 %所有长度单位为毫米 lamda=632.8e-6; k=2*pi/lamda; z=1000000; %先确定衍射屏 N=300; a=15; b=15; [m,n]=meshgrid(linspace(-N/2,N/2-1,N)); I=rect(m/(2*a)).*rect(n/(2*b)); q=exp(j*k*(m.^2+n.^2)/2/z); subplot(2,2,1); imagesc(I) colormap([0 0 0; 1 1 1]) axis image title('衍射屏形状') L=300; M=300; 若为圆孔，方框内替换为以下程序 r=12;a=1;b=1; I=zeros(N,N); [m,n]=meshgrid(linspace(-N/2,N/2-1,N)); D=((m-a).^2+(n-b).^2).^(1/2); i=find(D<=r); I(i)=1; %孔半径范围内透射系数为 1 %圆孔图像画在 2 行 2 列的第一个位置 %画衍射屏的形状 %颜色以黑白区分 %取相同点数用于矩阵运算 6

XX 大学 XXXX 学院 %圆孔频谱 %公式中为卷积，空间域中相卷相当于频域中相乘 %求逆变换，得到复振幅分布矩阵 %归一化 [x,y]=meshgrid(linspace(-L/2,L/2,M)); h=exp(j*k*z)*exp((j*k*(x.^2+y.^2))/(2*z))/(j*lamda*z);%接收屏 H =fftshift(fft2(h)); B=fftshift(fft2(I)); G=H.*B; U= fftshift(ifft2(G)); Br=(U/max(U)); subplot(2,2,2); imshow(abs(U)); axis image; colormap(hot) % figure,imshow(C); title('衍射后的图样'); subplot(2,2,3); mesh(x,y,abs(U)); subplot(2,2,4); plot(abs(Br)) %画三维图形 7

分享到：

赞收藏

资料库

圆孔矩孔的菲涅尔衍射模拟(matlab实现).docx

相关推荐

信息化

热门标签

最新资料