logo资料库

基于二次最优阈值近似消息传递法的蒸发波导去噪重构.pdf

发布时间：2022-05-30 发布人：admin 分类：说明书 资料大小：1.46M 资料格式：pdf 举报 版权申诉
第1页 / 共10页
第2页 / 共10页
第3页 / 共10页
第4页 / 共10页
第5页 / 共10页
第6页 / 共10页
第7页 / 共10页
第8页 / 共10页
资料共10页，剩余部分请下载后查看
    02-190268-®ýÜ.pdf
    第 40 卷第 10 期 2019 年 10 月 通 信 学 报 Journal on Communications Vol.40 No.10 October 2019 基于二次最优阈值近似消息传递法的蒸发波导去噪重构 芮国胜 1，刘歌 1，田文飚 1，董道广 1，张雅楠 2 （1. 海军航空大学信号与信息处理山东省重点实验室，山东 烟台 264501； 2. 93716 部队，天津 301716） 摘 要：针对蒸发波导时空态势感知过程中，压缩感知观测阶段混入噪声对高精度重构产生不利影响的问题，提 出了基于二次最优阈值的近似消息传递法。所提方法综合了软、硬阈值函数的优势，设计了一种二次稳固阈值函 数，改善 AMP 算法的重构性能，并在近似消息传递法的迭代过程中加入了基于共轭梯度法的最优阈值设置策略， 加快收敛速度。理论分析和实验表明，所提算法比现有的几种主流重构算法的收敛速度更快，去噪重建误差更小。 关键词：压缩感知；蒸发波导；去噪重构；近似消息传递法；阈值函数 中图分类号：TN911.73 文献标识码：A doi: 10.11959/j.issn.1000−436x.2019200 Denoising and reconstruction of evaporation duct based on quadratic optimal threshold approximation message passing method RUI Guosheng1, LIU Ge1, TIAN Wenbiao1, DONG Daoguang1, ZHANG Yanan2 1. Signal and Information Processing Key Laboratory in Shandong, Naval Aviation University, Yantai 264501, China 2. Unit 93716 of PLA, Tianjin 301716, China Abstract: To solve the problem that the mixed noise of compressed sensing observation stage had adverse effects on the high-precision reconstruction in the time-space situation awareness process of evaporative duct, an approximate message passing method based on quadratic optimal threshold was proposed. A quadratic stabilization threshold function which integrated advantages of soft and hard threshold functions was designed, and the optimal threshold setting policy was added to the iterative process based on conjugate gradient method to speed up convergence. Theoretical analysis and ex- periments show that, compared with several mainstream algorithms, the proposed algorithm has the faster convergence rate and lower denoising reconstruction error. Key words: compressed sensing, evaporation duct, denoising and reconstruction, approximate message passing, thresh- old function 1 引言 海面水蒸气蒸发会引起大气湿度随着高度的 增加而急剧减小，从而导致大气折射指数随高度逐 渐降低，形成近海面的大气异常结构，即蒸发波导。 蒸发波导能陷获无线电波，有助于实现超视距传 播，但可能造成频谱泄露，导致己方目标过早暴露[1]。 因此，蒸发波导的态势获取对海上舰船通信及岸舰 通信都具有极其重要的作用。在电磁空间被各方激 烈争夺的今天，获取各海域的蒸发波导态势迫在眉 睫。到目前为止，蒸发波导态势通常由诸如蒸发波 导的高度、强度和陷获频率范围等参数来描述，这 些参数是对传感器采集到的海面温度、压强、湿度、 风速等气象参数随时间的变化数据进行解算获得 的[2]，现有的传感器包括海上气象浮标、水文/气象 观测站[3]、卫星平台[4-5]等。文献[1]中详细分析了不 收稿日期：2019−05−14；修回日期：2019–08–11 基金项目：国家自然科学基金资助项目（No.41606117, No.41476089, No.61671016） Foundation Item: The National Natural Science Foundation of China (No.41606117, No.41476089, No.61671016) 2019200-1
    第 10 期 芮国胜等：基于二次最优阈值近似消息传递法的蒸发波导去噪重构 ·11· 同海域蒸发波导高度的分布特征及相关气象因子， 还分析了不同海域的全球蒸发波导高度特征形成 的原因。但实际上要获知蒸发波导的态势，仍然存 在很多问题。首先，要获取较高分辨率的蒸发波导 态势，需增大传感器密度，不仅浪费资源，且实现 十分困难。其次，现有的压缩体制需要采集全部信 息再进行计算，舍弃大系数保留小系数，这不仅会 造成资源浪费，还会增大编码端计算压力。压缩感 知为上述问题提供了有力的解决方案，田文飚等[6] 充分利用蒸发波导的时空稀疏性，提出利用压缩感 知对采集到的有限资源进行处理实现整体蒸发波 导态势感知，但是利用压缩感知实现蒸发波导态势 感知仍然存在着受噪声影响严重、重构精度不高的 问题。 近年来，一种新型迭代阈值算法——近似消息 传递（AMP, approximate message passing）[7]算法受 到越来越多的关注。它是 Donoho 受置信传播理论 的启发于 2009 年提出的，该算法能够在观测值数 量不多的情况下实现信号的高速重构，同时拥有 线性规划法的高相变性能和迭代阈值法的高速重 构性能。AMP 算法在其迭代的过程中并没有利用 信号自身的结构特征，而主要利用信号的稀疏分 布作为先验知识[8-9]。文献[10]中提出了一种去噪 AMP（D-AMP, denoising-based AMP）方法，可 以看作在 AMP 算法框架下的去噪延伸，并通过 理论特性分析和仿真实验证明，具有高性能去噪 功能的 AMP 算法的性能优于其他压缩感知重建 方法。但是上述 D-AMP 去噪函数都有相应的应 用场景限制，对蒸发波导参数重构的去噪效果和 收敛速度都不尽如人意。文献[11]提出了一种基 于高斯混合学习和去噪的 AMP 算法，研究了加 性高斯白噪声下的信号压缩感知去噪重构问题， 但是文中的去噪重构方法限定于输入统计量未知 的平稳遍历信号，难以适用于属于非平稳信号的 蒸发波导数据。 本文针对蒸发波导参数的去噪重构问题，提 出 了 一 种 基 于 二 次 最 优 阈 值 函 数 的 AMP （QOT-AMP, quadratic optimal threshold AMP）算 法，改善了原有 AMP 算法的重构性能，并设计 了一种基于共轭梯度法的最优阈值设置策略，使 其更快地收敛并以更高精度重构，理论上证明了 QOT-AMP 算法的收敛性，并通过实测数据进行 实验，验证了本文算法的有效性。 2 研究背景 2.1 压缩感知重构问题描述 压缩感知重构技术可以从已知的少量蒸发波 ，具 导参数观测值 y 中估计原蒸发波导数据 R N∈x 体表示为 y Ax v (1) = + 表示观测矩阵， v 表示观测噪声。 其中， R M N× 由于 M N< ，因此上述重构问题成为病态问题。 1 范数最小化问题的目标函数可以表示为 ∈， ∈A R M y ˆ x = arg min x 1 2 y Ax − 2 2 + ζ x 1 (2) 其中， 1x 表示信号 x 的 1 范数，ζ表示正则化参 数。已有一系列优化算法用来解决 1 范数最小化问 题，如梯度投影法[12]、基追踪法[13]、迭代阈值法[14] 等。其中，凸优化算法中的梯度投影法、基追踪法 具有较高的重构精度，但是计算时间复杂度较大， 实用性差；而迭代阈值算法更容易实现，计算量适 中且应用广泛。 2.2 近似消息传递法 作为一种新型的迭代阈值算法，AMP 算法的 表达形式类似于传统的迭代阈值算法。具体表达 式为 (3) x ) t t 1 τη+ = r t t ( x 1 ′ τη− + ( A r * x t 1 − A r * + m t 1 − ) 1 (4) t r = − y Ax t + 其中， tx 表示原信号 0x 的第 t 次迭代的估计值； ( )τη ⋅ 表示阈值函数，τ表示阈值参数，τ的取值决 定了整个迭代算法的性能； *A 表示观测矩阵的共轭 转 置 ； tr 表 示 第 t 次 迭 代 的 残 差 ， r A r * x 1 − 1 − ( ) t t t 1 ′ ξη− 1 被 称 为 Onsager 校 正 项 ， + m 表示采样率，Onsager 项中 ( )τη′ ⋅ 表示 ( )τη ⋅ 的 = Mm N 导数。由于 Onsager 项的存在，AMP 算法的收敛速 度更快，相变性能更高，且使 AMP 算法的性能可 以通过状态演化（SE, state evolution）[7]进行分析和 预测。 3 基于 QOT-AMP 的去噪重构算法 由于蒸发波导的各种重要参数（如高度、强度 2019200-2
    ·12· 通 信 学 报 第 40 卷 等）可以根据蒸发波导预测模型获得，具体模型计 算过程可参考文献[15-18]，本文忽略蒸发波导数据 预测模型计算的过程，直接将蒸发波导高度参数作 为压缩感知重构的对象。 压缩感知的基础是感知对象的稀疏性。目前， 对蒸发波导参数的稀疏性研究已经取得一定的进 展，文献[6]中利用离散余弦变换（DCT, discrete cosine transform）对蒸发波导参数进行稀疏性分析 且实现了重构，但仅在 DCT 域进行讨论，蒸发波 导稀疏性并没有被充分挖掘；文献[19]为了提升感 知的性能，提出一种递推的 KLT 基，将蒸发波导数 据的稀疏度约束到 4 以内，为后续的去噪重构奠定 稀疏性基础。 3.1 QST-AMP 算法 在上述稀疏性基础上，完全可以开展蒸发波导 参数的压缩感知重构算法研究。针对蒸发波导参数 观测过程中可能混入噪声的情况，未考虑去噪的重 构方法无法充分发挥作用，因此本文在 AMP 算法 的基础上，设计一种新的阈值函数对 AMP 进行改 进，以实现蒸发波导参数的去噪重构。 AMP 算法中 ( )τη ⋅ 通常采用软阈值函数和硬阈 值函数，这 2 种函数都已有相应的缺陷：软阈值函 数重构结果存在恒定误差，硬阈值函数是不连续 的。因此，本文针对 AMP 算法的阈值函数，设计 了二次函数线型，克服软硬阈值的缺陷，称为二次 阈值函数。 软阈值函数表达式为 soft( , ) τ x − x x sgn( )( ⎧ ⎪= ⎨ 0, < τ ⎪⎩ x ≥τ ), x τ 其中， soft( )⋅ 表示软阈值函数。 硬阈值函数的表达式为 ⎧ ⎨ ⎩ ≥x x , τ x 0, τ < 其中，hard(.)表示硬阈值函数。 hard(x,τ) = (5) (6) 文献[20]考虑将 2 种算法结合，构造了一种称 为稳固阈值函数的新阈值函数，如式(7)所示。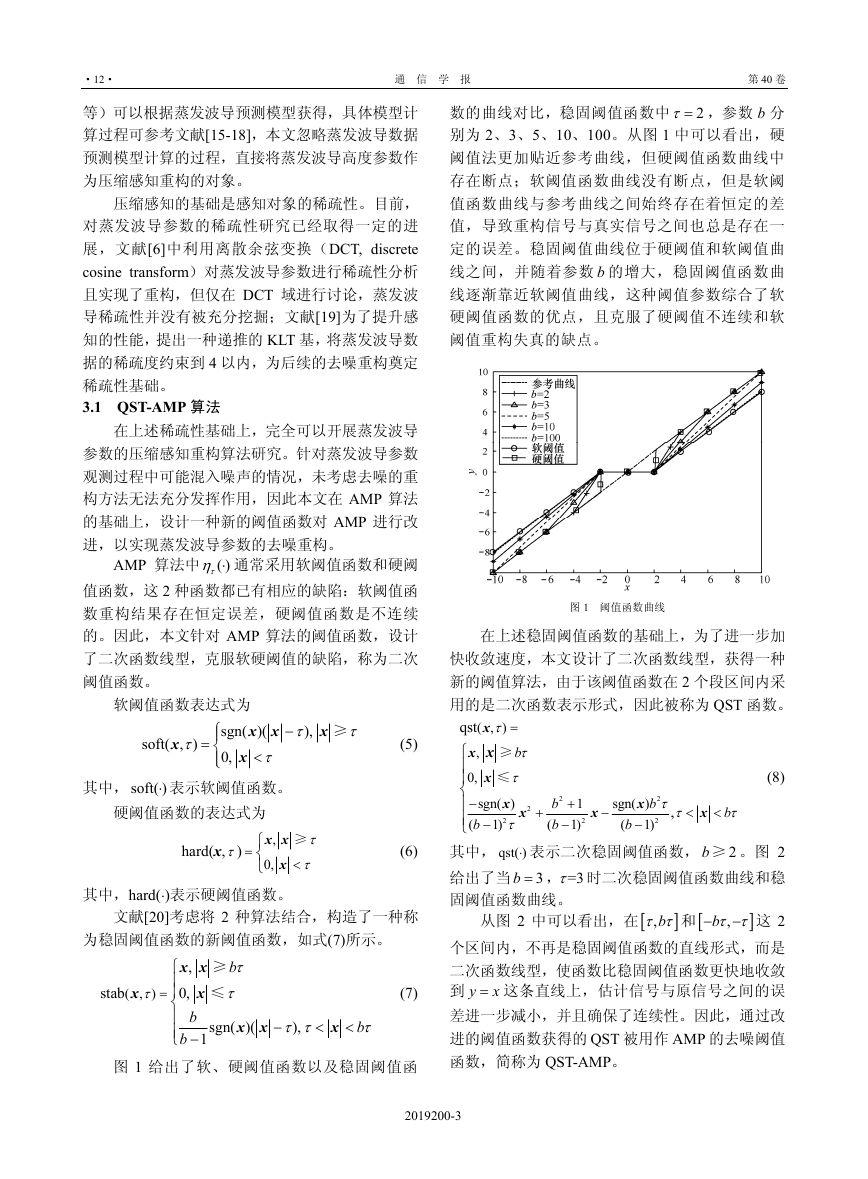 stab ( x , ) τ = x x , ⎧ ⎪ x 0, ⎪ ⎨ b ⎪ ⎪ −⎩ b 1 ≥ ≤ b τ τ (7) sgn( )( x x − τ τ ), < x < b τ 图 1 给出了软、硬阈值函数以及稳固阈值函 2019200-3 数的曲线对比，稳固阈值函数中 2τ= ，参数 b 分 别为 2、3、5、10、100。从图 1 中可以看出，硬 阈值法更加贴近参考曲线，但硬阈值函数曲线中 存在断点；软阈值函数曲线没有断点，但是软阈 值函数曲线与参考曲线之间始终存在着恒定的差 值，导致重构信号与真实信号之间也总是存在一 定的误差。稳固阈值曲线位于硬阈值和软阈值曲 线之间，并随着参数 b 的增大，稳固阈值函数曲 线逐渐靠近软阈值曲线，这种阈值参数综合了软 硬阈值函数的优点，且克服了硬阈值不连续和软 阈值重构失真的缺点。 图 1 阈值函数曲线 ≥ 在上述稳固阈值函数的基础上，为了进一步加 快收敛速度，本文设计了二次函数线型，获得一种 新的阈值算法，由于该阈值函数在 2 个段区间内采 用的是二次函数表示形式，因此被称为 QST 函数。 qst x ( , ) τ = x x b , ⎧ τ ⎪ x 0, ⎪ τ ≤ ⎨ x sgn( ) − ⎪ ⎪⎩ b ( 2 − τ b ≥ 。图 2 其中， qst( )⋅ 表示二次稳固阈值函数， 2 给出了当 3b = ， =3τ 时二次稳固阈值函数曲线和稳 固阈值函数曲线。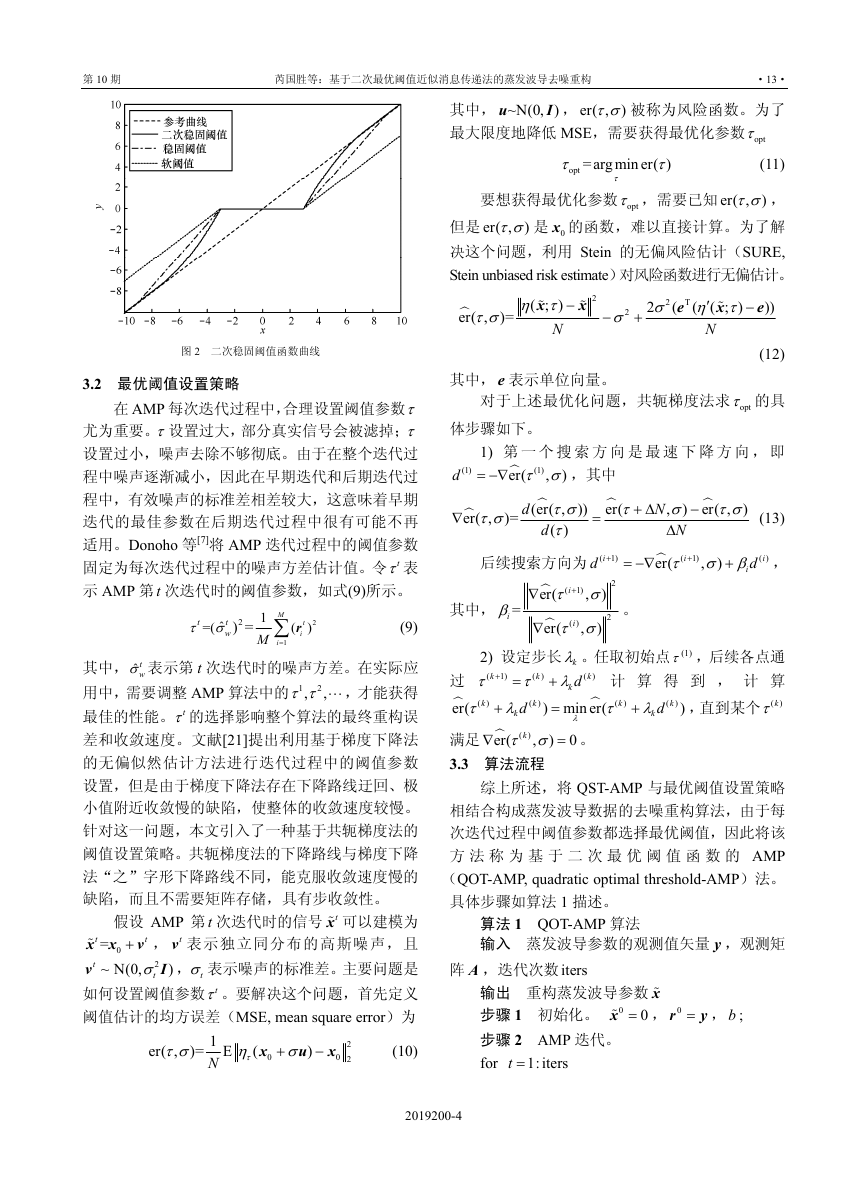 x b sgn( ) b 1) ( 2 − 1 + 1) 2 − 2 τ , τ b b ( (8) b τ 1) + 2 x − < x < 2 x 从图 2 中可以看出，在[ ,bτ τ 和[ ] − ] ,bτ τ − 这 2 个区间内，不再是稳固阈值函数的直线形式，而是 二次函数线型，使函数比稳固阈值函数更快地收敛 到 y x= 这条直线上，估计信号与原信号之间的误 差进一步减小，并且确保了连续性。因此，通过改 进的阈值函数获得的 QST 被用作 AMP 的去噪阈值 函数，简称为 QST-AMP。
    第 10 期 芮国胜等：基于二次最优阈值近似消息传递法的蒸发波导去噪重构 ·13· u I ， er( , )τσ 被称为风险函数。为了 其中， ~N(0, ) 最大限度地降低 MSE，需要获得最优化参数 optτ opt =arg min er( ) τ τ (11) τ 要想获得最优化参数 optτ ，需要已知 er( , )τσ ， )τσ 是 0x 的函数，难以直接计算。为了解 但是 er( , 决这个问题，利用 Stein 的无偏风险估计（SURE, Stein unbiased risk estimate）对风险函数进行无偏估计。 图 2 二次稳固阈值函数曲线 3.2 最优阈值设置策略 在 AMP 每次迭代过程中，合理设置阈值参数τ 尤为重要。τ设置过大，部分真实信号会被滤掉；τ 设置过小，噪声去除不够彻底。由于在整个迭代过 程中噪声逐渐减小，因此在早期迭代和后期迭代过 程中，有效噪声的标准差相差较大，这意味着早期 迭代的最佳参数在后期迭代过程中很有可能不再 适用。Donoho 等[7]将 AMP 迭代过程中的阈值参数 固定为每次迭代过程中的噪声方差估计值。令 tτ 表 示 AMP 第 t 次迭代时的阈值参数，如式(9)所示。 t t ˆ=( τ σ w ) = 2 1 M M ∑ r ( i i 1 = t 2 ) (9) 2 , wσ 表示第 t 次迭代时的噪声方差。在实际应 其中， ˆ t 用中，需要调整 AMP 算法中的 1 ,τ τ ，才能获得 最佳的性能。 tτ 的选择影响整个算法的最终重构误 差和收敛速度。文献[21]提出利用基于梯度下降法 的无偏似然估计方法进行迭代过程中的阈值参数 设置，但是由于梯度下降法存在下降路线迂回、极 小值附近收敛慢的缺陷，使整体的收敛速度较慢。 针对这一问题，本文引入了一种基于共轭梯度法的 阈值设置策略。共轭梯度法的下降路线与梯度下降 法“之”字形下降路线不同，能克服收敛速度慢的 缺陷，而且不需要矩阵存储，具有步收敛性。 假设 AMP 第 t 次迭代时的信号 tx 可以建模为 ， tv 表示独立同分布的高斯噪声，且 x x v 0=t t+ v I ， tσ 表示噪声的标准差。主要问题是 ) ~ N(0, t 2 tσ 如何设置阈值参数 tτ 。要解决这个问题，首先定义 阈值估计的均方误差（MSE, mean square error）为 er( , τσ )= 1 N E η τ ( x 0 u σ+ ) − x 2 0 2 (10) 2019200-4 er( , τσ )= 2 − x x ( ; ) η τ N − 2 σ + 其中， e 表示单位向量。 2 T ( ( e x ( ; ) 2 ′ σ η τ N − e )) (12) 对于上述最优化问题，共轭梯度法求 optτ 的具 体步骤如下。 1) 第 一 个 搜 索 方 向 是 最 速 下 降 方 向 ， 即 = −∇ ) τ σ er( (1) (1) d er( , τσ )= ∇ d ，其中 er( , (er( , )) τσ d ( ) τ = τ N + Δ ) , σ N Δ er( , ) τσ − (13) 后续搜索方向为 i ( 1) + d = −∇ er( + i ( 1) d τ σ β i + ) , i ( ) ， 其中， β i = ∇ + , i ( 1) ) er( τ σ er( ) τ σ i ( ) , ∇ 2 2 。 k ( ) k ( ) + ) min er( = 2) 设定步长 kλ 。任取初始点 (1)τ ，后续各点通 kd k 过 ( 1) + = τ τ λ 计 算 得 到 ， 计 算 d er( k ，直到某个 ( )kτ k k ( ) ( ) ( ) τ λ + τ λ k k 满足 ( ) ) kτ σ 3.3 算法流程 = 。 λ 0 er( ∇ + d k ( ) ) , 综上所述，将 QST-AMP 与最优阈值设置策略 相结合构成蒸发波导数据的去噪重构算法，由于每 次迭代过程中阈值参数都选择最优阈值，因此将该 方 法 称 为 基 于 二 次 最 优 阈 值 函 数 的 AMP （QOT-AMP, quadratic optimal threshold-AMP）法。 具体步骤如算法 1 描述。 算法 1 QOT-AMP 算法 输入 蒸发波导参数的观测值矢量 y ，观测矩 阵 A ，迭代次数 iters 输出 重构蒸发波导参数 x 步骤 1 初始化。 步骤 2 AMP 迭代。 for 1: iters 0=x 0 t = ， 0 =r y ， b ;
    ·14· t 1 − q = ( t σ− ) 1 2 t 1 − t 1 − i ( ) t 1 − x A r T + 1 M = ∑r M i 1 = ) 1 2 − t t 1 ( = q qst( bτ− , , ) 1 t τ σ− tτ− 。 利用共轭梯度法获得最优值 1 opt =x t I ， 并 取 生 成 N 维 随 机 列 向 量 N(0, ) q t 1 − ) − ∞ 1 000 ∈h b , t 1 − τ τ + opt υ T (qst( On- div t 1 − opt ， h = q x 1 − ) t t t = υ sager 项更新 onsager t r t 1 −= t div M onsager t t r + − y Ax 残差更新 =t end for 步骤 3 输出。得到蒸发波导参数向量 x 。 3.4 算法收敛性分析 由文献[10]对 AMP 算法中去噪阈值函数的性 质描述可知，阈值函数需要满足单调性和 Lipschitz 连续性，其中，单调性很容易可以得出，本文重点 对其 Lipschitz 连续性进行证明。Lipschitz 连续性的 f x ，如果存在一个常量 K 定义为：对于函数 ( ) （ 0K > ），使 ( ) 上的任意 2 个值满足 f x (14) ( ) − 1 f x 的 Lipschitz 常数。证明 QST 函 其中， K 为 ( ) 数的 Lipschitz 连续性，则需要证明 K x 1 f x 在定义域（可为实数也可为复数） , ) qst( τ K x 1 (15) f x ( 2 qst( , ) τ x 2 x 2 x 2 ≤ ≤ x 1 − − ) − 具体证明如下。 1) 当 x bτ≥ 时 qst( qst( , )= 2 2 x x − + τ xτ x qst( , )= bτ > ≥ x x 令 1 ， 在 2 x x x K x , ) qst( , ) τ τ − ≤ 2 1 2 1 xτ 2) 当 < 时 b τ < x b sgn( ) 1 − + b b 1) ( ( 1) 2 2 τ − − x x ，有 τ τ < b < < 1 2 x x qst( , ) qst( , ) τ = τ 2 1 x sgn( ) b 1 2 − + 1 b b ( ( 1) 1) 2 2 − − τ x sgn( ) b 1 2 − + 1 b b 1) ( ( 1) 2 2 − − τ x 2 1 x 2 x 2 令 x 1 − − + − 2 + x (16) 0K > 时 满 足 。 − x b sgn( ) 2 τ b ( 1) 2 − (17) 2 τ − x b sgn( ) 1 b 1) ( 2 − x b sgn( ) 2 b 1) ( 2 − 2 τ = 2019200-5 通 信 学 报 第 40 卷 sgn( 2 x x )( 1 2 b 1) ( − x ) − 2 1) 2 − b ( x ( 1 b ( − 2 τ x 2 1 ) + b b ( 2 2 1 ( + 1) − ( x 1 2 1 sgn( + − x 1 ) 因为 τ < x 1 < x 2 < b τ ，所以 2 < x 1 − x 2 ) = + τ x 2 ) ) (18) ( x 1 x 2 ) + τ < 。 b 2 那么，有 x , ) qst( qst( τ − 1 x x ( ) − 1 2 b 1) ( 2 − b ( 2 x 2 , ) τ < 1 2 sgn( + − b 因 此 ， 当 x 1 )) = x ( 1 b ( − − x ) 2 1) 2 b ( − sgn( x 1 2 )) K ≥ b ( 2 )) x sgn( − 1 b ( 1) 2 − (19) 即 K ≥ x 1 τ ⎧ < ， 1 ⎪ b 1) ( 2 + ⎨ ⎪ b 1) ( − ⎩ 连续条件。 3) 当 x 2 < x 2 < b τ − ， b τ < x 2 < x 1 时，满足 Lipschitz < − τ τ−≤ 时 ， qst( , )=0 x τ ， 仍 然 满 足 Lipschitz 连续条件。 4) 在各分段点处皆满足 Lipschitz 连续条件。 综上所述，QST 函数满足 Lipschitz 连续条件。 QOT-AMP 算法的收敛性可以通过状态演变 （SE, state evolution）方程进行检验。SE 方程是用 来分析 AMP 算法性能的关键，一系列的 SE 方程可 以 预 测 AMP 算 法 在 每 一 次 迭 代 过 程 中 产 生 的 2 2 MSE，以确保整个迭代过程的收敛性。从 0 θ = x 0 n 开始，SE 通过以下迭代产生一系列数值。 1 + t θ ( x 0 , 2 δσ w , ) = E η τ ( x 0 + t ) τε − 2 x 0 2 (20) 其 中 ， ( t σ ) 2 = t xθ δσ 2 w 0( , ) + ， ~N(0,I) 2 σ w ε 。 t 1 + xθ 0( , 2 δσ w 观测噪声 2 , wσ 有关。 ) 表明 tθ 与信号 0x 、不确定参数δ以及 考虑到 AMP 去噪的迭代过程， tx 表示第 t 次 迭代信号的估计值。文献[10]通过大量的实验发现， x 开始，那么，SE 如果 AMP 去噪迭代过程从 0 =0 过程估计 AMP 去噪过程的均方差可以近似为 t xθ δσ ≈ 0( 2 w ) , , 1 n tx − 2 x 0 2 (21) 式(21)能够成立是建立在满足以下 3 个条件的 1 n , δ
    第 10 期 芮国胜等：基于二次最优阈值近似消息传递法的蒸发波导去噪重构 ·15· 基础之上的[10]。1) 观测矩阵 A 是独立同分布的均值 为 0 的高斯矩阵； 2) 噪声 w 服从独立同分布的高 斯分布；3) 去噪阈值函数是 Lipschitz 连续函数。根 据本文描述，上述 3 个条件已满足。图 3 给出了基 于二次稳固阈值函数与软阈值函数的 AMP 算法的 状态演变曲线和文献[21]中的状态演变曲线的比较。 测试信号的长度为 1 000，稀疏度为 10，观测比率为 0.3。图 3 中 tau2 曲线表示算法的有效噪声方差，MSE 表示算法的均方误差，SE-tau2 和 SE-MSE 分别表示 状态演变方程预测的有效噪声方差和 SE-MSE 表示 状 态 演 变 方 程 预 测 的 均 方 误 差 。 对 比 来 看 ， QOT-AMP 的残差能量和均方误差均低于 soft-AMP 和文献[21]中的算法。QOT-AMP 方法的收敛速度较 快，在第 2 次迭代时已经实现收敛。 反映了算法重构信号后的准确性，RSNR 定义为 RSNR 10lg = ⎛ ⎜ ⎜ ⎝ x − 2 ˆ x x ⎞ ⎟ ⎟ ⎠ 2 (22) 在信噪比在[−10,20]dB 范围内以 5 dB 为间隔， 分别对 5 种重构算法进行 1 000 次蒙特卡洛仿真实 验。其中，QOT-AMP 与 soft-AMP 算法中的迭代次 数设置为 30 次。图 4 给出了 7 种重构算法下的 RSNR 随噪声变化的性能曲线，可以看出随着信噪比的增 加，重构算法的重构信噪比都呈上升趋势，其中， QOT-AMP 算法具有最佳的重构性能和最佳的抗噪 性能，OMP 的重构性能最差，NLM-AMP 和 AMP-UD 算法的性能相当，次于 QOT-AMP 算法。NLM-AMP 方法是文献[10]将 NLM 去噪器加入 AMP 中的一种 处 理 一 维 信 号 的 去 噪 算 法 ， 去 噪 重 构 性 能 优 于 soft-AMP 和 SP，AMP-UD 是文献[11]中提出的一种 去噪重构方法，重构性能仅次于 QOT-AMP。 图 3 SE 曲线对比 4 性能分析及仿真实验 4.1 测试信号的去噪重构仿真分析 为了验证本文算法的有效性，分别在不同信噪 比和不同稀疏度的条件下，将本文算法 QOT-AMP 与 6 种重构算法进行比较。用于对比实验的算法分 别是 OMP、NLM-AMP[10]、AMP-UD[11]、SP[22]、 CoSaMP[23]、soft-AMP（AMP 的去噪函数为软阈值 函数），其中，OMP 来自 SparseLab 软件包。 4.1.1 去噪重构精确度分析 以仿真信号为实验研究对象，首先研究了不同 重构算法随信噪比的变化情况。取长度为 1 024 点 的一维稀疏测试信号，采样速率设定为 Nyquist 速 率的 20%，即观测数与信号长度之比为 0.2，稀疏 k = 。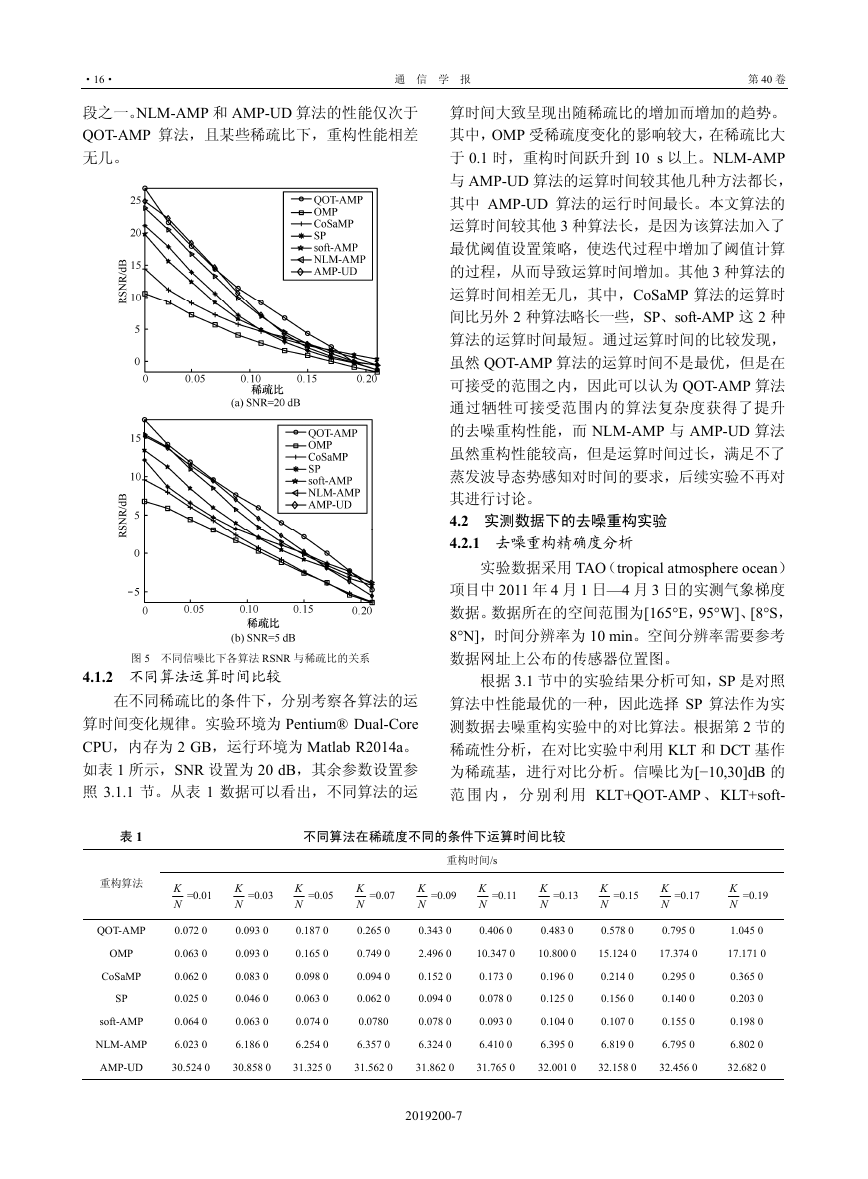重构信噪比（RSNR, reconstruction-SNR） 度 50 图 4 相同稀疏度下各算法 RSNR 与 SNR 关系曲线 然后，研究了信号稀疏性对重构性能的影响。 稀疏度通过稀疏比 K （非零元素的个数与信号长度 N 的比值）来表示。测试信号的稀疏比在[0.01,0.21] 的范围内以 0.02 的间隔变化，信号的信噪比设置为 5 dB 和 20 dB，各重构算法的参数设置与上一个实 验相同，分别进行 1 000 次的蒙特卡洛实验。图 5 中给出了仿真实验的结果。从曲线总体变化情况来 看，几种算法的重构性能随着稀疏比的减小而增 大，即信号越稀疏重构性能越高。其中，QOT-AMP 算法的重构性能最好，且信号越稀疏，精确重构的 优势越明显。然而，随着稀疏比的增大，QOT-AMP 算法的重构性能受影响较大。因此从侧面证明了探 索待处理信号的稀疏性是保证重构精度的重要手 2019200-6
    ·16· 通 信 学 报 第 40 卷 段之一。NLM-AMP 和 AMP-UD 算法的性能仅次于 QOT-AMP 算法，且某些稀疏比下，重构性能相差 无几。 图 5 不同信噪比下各算法 RSNR 与稀疏比的关系 4.1.2 不同算法运算时间比较 在不同稀疏比的条件下，分别考察各算法的运 算时间变化规律。实验环境为 Pentium® Dual-Core CPU，内存为 2 GB，运行环境为 Matlab R2014a。 如表 1 所示，SNR 设置为 20 dB，其余参数设置参 照 3.1.1 节。从表 1 数据可以看出，不同算法的运 算时间大致呈现出随稀疏比的增加而增加的趋势。 其中，OMP 受稀疏度变化的影响较大，在稀疏比大 于 0.1 时，重构时间跃升到 10 s 以上。NLM-AMP 与 AMP-UD 算法的运算时间较其他几种方法都长， 其中 AMP-UD 算法的运行时间最长。本文算法的 运算时间较其他 3 种算法长，是因为该算法加入了 最优阈值设置策略，使迭代过程中增加了阈值计算 的过程，从而导致运算时间增加。其他 3 种算法的 运算时间相差无几，其中，CoSaMP 算法的运算时 间比另外 2 种算法略长一些，SP、soft-AMP 这 2 种 算法的运算时间最短。通过运算时间的比较发现， 虽然 QOT-AMP 算法的运算时间不是最优，但是在 可接受的范围之内，因此可以认为 QOT-AMP 算法 通过牺牲可接受范围内的算法复杂度获得了提升 的去噪重构性能，而 NLM-AMP 与 AMP-UD 算法 虽然重构性能较高，但是运算时间过长，满足不了 蒸发波导态势感知对时间的要求，后续实验不再对 其进行讨论。 4.2 实测数据下的去噪重构实验 4.2.1 去噪重构精确度分析 实验数据采用 TAO（tropical atmosphere ocean） 项目中 2011 年 4 月 1 日—4 月 3 日的实测气象梯度 数据。数据所在的空间范围为[165°E，95°W]、[8°S， 8°N]，时间分辨率为 10 min。空间分辨率需要参考 数据网址上公布的传感器位置图。 根据 3.1 节中的实验结果分析可知，SP 是对照 算法中性能最优的一种，因此选择 SP 算法作为实 测数据去噪重构实验中的对比算法。根据第 2 节的 稀疏性分析，在对比实验中利用 KLT 和 DCT 基作 为稀疏基，进行对比分析。信噪比为[−10,30]dB 的 范 围 内 ， 分 别 利 用 KLT+QOT-AMP 、KLT+soft- 表 1 重构算法 QOT-AMP OMP CoSaMP SP soft-AMP NLM-AMP 不同算法在稀疏度不同的条件下运算时间比较 重构时间/s K N =0.01 K N =0.03 K N =0.05 K N =0.07 K N =0.09 K N =0.11 K N =0.13 K N =0.15 K N =0.17 K N =0.19 0.072 0 0.063 0 0.062 0 0.025 0 0.064 0 6.023 0 0.093 0 0.093 0 0.083 0 0.046 0 0.063 0 6.186 0 0.187 0 0.165 0 0.098 0 0.063 0 0.074 0 6.254 0 0.265 0 0.749 0 0.094 0 0.062 0 0.0780 6.357 0 0.343 0 2.496 0 0.152 0 0.094 0 0.078 0 6.324 0 0.406 0 0.483 0 0.578 0 0.795 0 1.045 0 10.347 0 10.800 0 15.124 0 17.374 0 17.171 0 0.173 0 0.078 0 0.093 0 6.410 0 0.196 0 0.125 0 0.104 0 6.395 0 0.214 0 0.295 0 0.365 0 0.156 0 0.107 0 6.819 0 0.140 0 0.155 0 6.795 0 0.203 0 0.198 0 6.802 0 AMP-UD 30.524 0 30.858 0 31.325 0 31.562 0 31.862 0 31.765 0 32.001 0 32.158 0 32.456 0 32.682 0 2019200-7
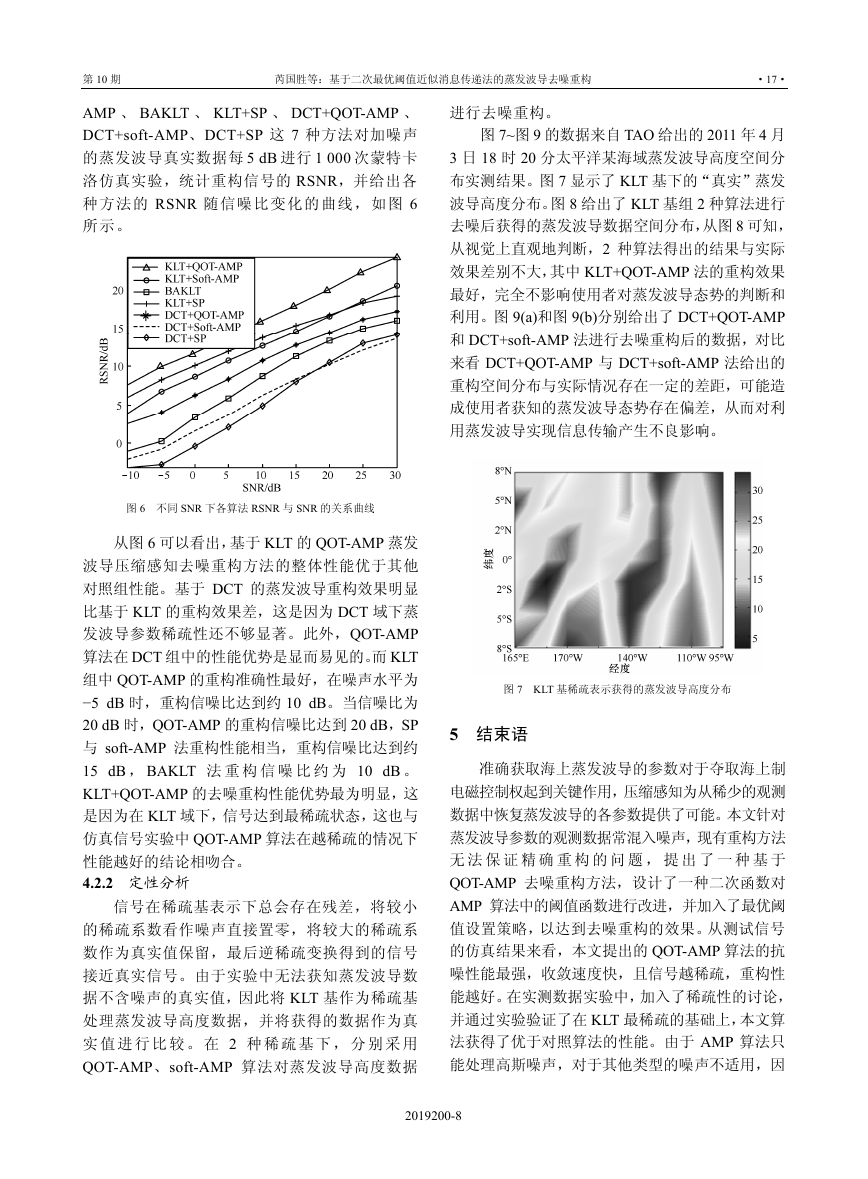
    第 10 期 芮国胜等：基于二次最优阈值近似消息传递法的蒸发波导去噪重构 ·17· AMP 、 BAKLT 、 KLT+SP 、 DCT+QOT-AMP 、 DCT+soft-AMP、DCT+SP 这 7 种方法对加噪声 的蒸发波导真实数据每 5 dB 进行 1 000 次蒙特卡 洛仿真实验，统计重构信号的 RSNR，并给出各 种方法的 RSNR 随信噪比变化的曲线，如图 6 所示。 图 6 不同 SNR 下各算法 RSNR 与 SNR 的关系曲线 从图 6 可以看出，基于 KLT 的 QOT-AMP 蒸发 波导压缩感知去噪重构方法的整体性能优于其他 对照组性能。基于 DCT 的蒸发波导重构效果明显 比基于 KLT 的重构效果差，这是因为 DCT 域下蒸 发波导参数稀疏性还不够显著。此外，QOT-AMP 算法在 DCT 组中的性能优势是显而易见的。而 KLT 组中 QOT-AMP 的重构准确性最好，在噪声水平为 −5 dB 时，重构信噪比达到约 10 dB。当信噪比为 20 dB 时，QOT-AMP 的重构信噪比达到 20 dB，SP 与 soft-AMP 法重构性能相当，重构信噪比达到约 15 dB ， BAKLT 法 重 构 信 噪 比 约 为 10 dB 。 KLT+QOT-AMP 的去噪重构性能优势最为明显，这 是因为在 KLT 域下，信号达到最稀疏状态，这也与 仿真信号实验中 QOT-AMP 算法在越稀疏的情况下 性能越好的结论相吻合。 4.2.2 定性分析 信号在稀疏基表示下总会存在残差，将较小 的稀疏系数看作噪声直接置零，将较大的稀疏系 数作为真实值保留，最后逆稀疏变换得到的信号 接近真实信号。由于实验中无法获知蒸发波导数 据不含噪声的真实值，因此将 KLT 基作为稀疏基 处理蒸发波导高度数据，并将获得的数据作为真 实 值 进 行 比 较 。 在 2 种 稀 疏 基 下 ， 分 别 采 用 QOT-AMP、soft-AMP 算法对蒸发波导高度数据 进行去噪重构。 图 7~图 9 的数据来自 TAO 给出的 2011 年 4 月 3 日 18 时 20 分太平洋某海域蒸发波导高度空间分 布实测结果。图 7 显示了 KLT 基下的“真实”蒸发 波导高度分布。图 8 给出了 KLT 基组 2 种算法进行 去噪后获得的蒸发波导数据空间分布，从图 8 可知， 从视觉上直观地判断，2 种算法得出的结果与实际 效果差别不大，其中 KLT+QOT-AMP 法的重构效果 最好，完全不影响使用者对蒸发波导态势的判断和 利用。图 9(a)和图 9(b)分别给出了 DCT+QOT-AMP 和 DCT+soft-AMP 法进行去噪重构后的数据，对比 来看 DCT+QOT-AMP 与 DCT+soft-AMP 法给出的 重构空间分布与实际情况存在一定的差距，可能造 成使用者获知的蒸发波导态势存在偏差，从而对利 用蒸发波导实现信息传输产生不良影响。 图 7 KLT 基稀疏表示获得的蒸发波导高度分布 5 结束语 准确获取海上蒸发波导的参数对于夺取海上制 电磁控制权起到关键作用，压缩感知为从稀少的观测 数据中恢复蒸发波导的各参数提供了可能。本文针对 蒸发波导参数的观测数据常混入噪声，现有重构方法 无 法 保 证 精 确 重 构 的 问 题 ， 提 出 了 一 种 基 于 QOT-AMP 去噪重构方法，设计了一种二次函数对 AMP 算法中的阈值函数进行改进，并加入了最优阈 值设置策略，以达到去噪重构的效果。从测试信号 的仿真结果来看，本文提出的 QOT-AMP 算法的抗 噪性能最强，收敛速度快，且信号越稀疏，重构性 能越好。在实测数据实验中，加入了稀疏性的讨论， 并通过实验验证了在 KLT 最稀疏的基础上，本文算 法获得了优于对照算法的性能。由于 AMP 算法只 能处理高斯噪声，对于其他类型的噪声不适用，因 2019200-8
    分享到：
    赞 收藏

    相关推荐

    资料库

    开发技术

    共收录19306份资料，累计14个分类，关注成员有19位，主要包括：Actionscript,Javascript,PHP,VB,Perl,Delphi,Python,C#,C,Java,C++,Web开发,硬件开发,其它

    热门标签

    Actionscript Javascript PHP VB Perl Delphi Python C# C Java C++ Web开发 硬件开发 其它

    最新资料