第 ２８ 卷第 ９ 期 ２０１１ 年 ９ 月　 计 算 机 应 用 研 究 Ａｐｐｌｉｃａｔｉｏｎ Ｒｅｓｅａｒｃｈ ｏｆ Ｃｏｍｐｕｔｅｒｓ 基 于 AGA 的 时 间 最 优 机 械 臂 轨 迹 规 划 算 法 付　荣， 居鹤华 （北京工业大学 电子信息与控制工程学院， 北京 １００１２４） Ｖｏｌ．２８ Ｎｏ．９ Ｓｅｐ．２０１１ 倡 ＦＵ Ｒｏｎｇ， ＪＵ Ｈｅ唱ｈｕａ 虑关节速度和加速度等约束条件下运用遗传算法对各分段轨 摘　要： 根据机械臂运动学约束，提出了关节空间基于自适应遗传算法（ＡＧＡ）的 ３唱５唱３ 多项式插值轨迹规划算 法。 利用运动学约束，以最优时间为目标，针对关节型机器人在静态环境下点到点的轨迹规划问题，利用 ＡＧＡ 算法解算多项式插值的时间。 通过与基于 ＧＡ 的３唱５唱３ 多项式机械臂轨迹规划进化曲线和运动位置、速度、加速 度曲线对比，证明该方法在算法收敛、运行平稳度上都有突出优点。 关键词： 机械臂； 轨迹规划； 时间最优； 自适应遗传算法； 多项式插值 中图分类号： ＴＰ２４２畅２　　　文献标志码： Ａ　　　文章编号： １００１唱３６９５（２０１１）０９唱３２７５唱０４ ｄｏｉ：１０．３９６９／ｊ．ｉｓｓｎ．１００１唱３６９５．２０１１．０９．０１９ Ｔｉｍｅ唱ｏｐｔｉｍａｌ ｔｒａｊｅｃｔｏｒｙ ｐｌａｎｎｉｎｇ ａｌｇｏｒｉｔｈｍ ｂａｓｅｄ ｏｎ ＡＧＡ ｆｏｒ ｍａｎｉｐｕｌａｔｏｒ （College of Electronic Information ＆ Control Engineering， Beijing University of Technology， Beijing １００１２４， China） Abstract： Ａｃｃｏｒｄｉｎｇ ｔｏ ｔｈｅ ｖｅｌｏｃｉｔｙ ｌｉｍｉｔａｔｉｏｎ ｏｆ ｍａｎｉｐｕｌａｔｏｒ， ｐｒｏｐｏｓｅｄ ａ ｔｉｍｅ唱ｏｐｔｉｍａｌ ３唱５唱３ ｐｏｌｙｎｏｍｉａｌ ｉｎｔｅｒｐｏｌａｔｉｏｎ ｔｒａｊｅｃ唱 ｔｏｒｙ ｐｌａｎｎｉｎｇ ａｌｇｏｒｉｔｈｍ ｂａｓｅｄ ｏｎ ａｄａｐｔｉｖｅ ｇｅｎｅｔｉｃ ａｌｇｏｒｉｔｈｍ （ＡＧＡ）．Ｔｏ ｐｌａｎ ｔｈｅ ｐｏｉｎｔ唱ｔｏ唱ｐｏｉｎｔ ｔｒａｊｅｃｔｏｒｉｅｓ ｆｏｒ ｍａｎｉｐｕｌａｔｏｒ ｗｏｒｋｉｎｇ ｉｎ ａ ｓｔａｔｉｃ ｅｎｖｉｒｏｎｍｅｎｔ ｆｏｒ ｔｉｍｅ唱ｏｐｔｉｍａｌ， ｕｓｅｄ ＡＧＡ ｔｏ ｇｅｔ ｔｈｅ ｔｉｍｅ ｏｆ ｐｏｌｙｎｏｍｉａｌ ｉｎｔｅｒｐｏｌａｔｉｏｎ．Ｔｈｅ ｓｉｍｕｌａｔｉｏｎ ｒｅｓｕｌｔｓ ｓｈｏｗ ｔｈａｔ ｔｈｅ ａｌｇｏｒｉｔｈｍ ｈａｓ ｇｏｏｄ ｐｅｒｆｏｒｍａｎｃｅ ｏｎ ｔｉｍｅ唱ｏｐｔｉｍａｌ ａｎｄ ｓｔａｂｉｌｉｔｙ ｃｏｍｐａｒｅｄ ｗｉｔｈ ３唱５唱３ ｐｏｌｙｎｏｍｉａｌ ｉｎｔｅｒｐｏｌａｔｉｏｎ ｔｒａｊ唱 ｅｃｔｏｒｙ ｐｌａｎｎｉｎｇ ａｌｇｏｒｉｔｈｍ ｂａｓｅｄ ｏｎ ｓｉｍｐｌｅ ｇｅｎｅｔｉｃ ａｌｇｏｒｉｔｈｍ． Key words： ｍａｎｉｐｕｌａｔｏｒ； ｔｒａｊｅｃｔｏｒｙ ｐｌａｎｎｉｎｇ； ｔｉｍｅ唱ｏｐｔｉｍａｌ； ａｄａｐｔｉｖｅ ｇｅｎｅｔｉｃ ａｌｇｏｒｉｔｈｍ（ＡＧＡ）； ｐｏｌｙｎｏｍｉａｌ ｉｎｔｅｒｐｏｌａｔｉｏｎ 　　遗传算法是模拟生物在自然环境中的遗传和进化过程而 形成的一种全局优化概率搜索算法。 其搜索不依赖于梯度信 息，尤其适用于处理传统搜索方法难于解决的复杂和非线性问 题，所需的领域知识少，具有很强的鲁棒性。 传统的遗传算法 由于使用固定的交叉概率 Pc 和变异概率 Pm，存在无法兼顾算 法的收敛速度和全局最优的问题。 对自适应遗传算法，国内外 已有很多学者进行了研究。 Ｓｒｉｎｉｖａｓ 等人 算法能够在优化过程中自适应地改变 Pc 和 Pm 值，在种群趋向 于最优时，增大 Pc 和 Pm 值，而在种群离散于解空间时，减小 Pc 和 Pm 值，便能达到全局最优和快速收敛的效果。 刘智明等 ［２］ 了余弦改进形式的自适应遗传算子。 喻寿益等人 式模糊自适应遗传算法，在一定程度上改善了自适应遗传算法 的不足。 多项式插值函数计算简单，唱常用于机械臂轨迹规划。 分 段多项式插值函数中，满足轨迹位置、速度、加速度连续且多项 式次数最低的分段多项式组合为三次样条插值为 ３唱３唱３唱３唱３ 插值、３ 段３唱５唱３ 多项式插值和 ４唱３唱４ 多项式插值。 恽为民等 将遗传算法优化引入动力学模型，提出了最小时间的机 ［５］ （１） 器人轨迹优化方法。 将甘亚辉等人 （２） 优轨迹规划，利用遗传算法方法优化４唱４唱…唱４唱５ 多项式规划 （３） 运行轨迹实现机械臂避障功能。 其对象为简单的平面关节机 未知系数 aj１i、aj２i、aj３i为第 j 个关节轨迹第一段、第二段、第 械臂，且多项式插值系数高，计算量大。 张勇等人 三段插值函数的第 i 个系数，hj１（t）、hj２（t）、hj３（t）分别代表第 j 自适应遗传算法优化三次样条插值的并联机械臂轨迹规划，考 　　收稿日期： ２０１１唱０３唱０３； 修 回 日 期： ２０１１唱０４唱２３　　 基 金 项 目： 国 家“８６３” 计 划 资 助 项 目（２００８ＡＡ００８５）； 国 家 自 然 科 学 基 金 资 助 项 目 （６０９７５０６５） 　　作者简介：付荣（１９８６唱），女，北京怀柔人，硕士，主要研究方向为机械 臂轨迹规划（ｇｉｇｇｌｅｆｕｒｏｎｇ＠ｙａｈｏｏ．ｃｏｍ．ｃｎ）；居鹤华（１９６９唱），男，教授，博 士，主要研究方向为机器人自主运动控制． 迹时间间隔进行了优化。 但三次样条插值不能使加速度连续。 提出了基于 ＩＡＧＡ 的机械手时间最优轨迹规划， 但该方法没有与多项式插值结合，虽然改进的自适应方法可以 改善遗传算法的收敛效果，但是机械臂的运行效果并不理想。 综合考虑计算量和高次多项式带来的不稳定性，本文根据 三自由度机械臂运动学约束，提出了关节空间基于自适应遗传 算法（ＡＧＡ）的３唱５唱３ 多项式插值轨迹规划算法。 针对Ｂ２ 型月 实验，基于 ＧＡ 的 ３唱５唱３ 多项式机械臂轨迹规划收敛速度、运 动位置、速度、加速度曲线对比，证明该方法在以上性能方面有 突出优点。 1　3唱5唱3 样条插值函数的构造 一般来说，样条曲线是在插值点具有 k －１ 阶导数连续性 的 k 次多项式。 对于多项式样条函数，一阶导数代表速度的连 续性，二阶导数代表加速度的连续性，三阶导数代表脉动。 hj２（t） ＝aj２５ t５ ＋aj２４ t４ ＋aj２３ t３ ＋aj２２ t２ ＋aj２１t１ ＋aj２０ hj３（t） ＝aj３３ t３ ＋aj３２t２ ＋aj３１ t１ ＋aj３０　j ＝１，２，３，４，n 提出基于排序的改进自适应遗传算法。 石山等人 ［４］ ［３］ 球车上驱动相机盒运动的六自由度正交解耦机械臂进行仿真 ３唱５唱３ 样条多项式的通式为 hj１（t） ＝aj１３ t３ ＋aj１２ t２ ＋aj１１ t１ ＋aj１０ ［１］ 提出的自适应遗传 人 人 周小燕等人 ［８］ 研究 提出嵌套 ［６］ 提出多机器人系统的最 ［７］ 提出利用 

计 算 机 应 用 研 究 　 置是笛卡尔系下机械臂运动的空间坐标通过逆运动学解算得 ·６７２３· 段关节的第一段三次多项式轨迹、第二段五次多项式轨迹和第 三段三次多项式轨迹，n 表示关节个数。 Tj、Jj、Aj、Vj、Xj 表示第 j 段关节插值的时间、脉动、加速度、速度和位置。 Xj 表示的位 出的关节角度。 已知条件为第 j 个关节各段的初始点 Xj０、路径 点 Xj１和 Xj２、末端点 Xj３ 以及初始点和终点的加速度、速度 Aj０、 Aj３、Vj０、Vj３（一般取为０）。 路径点之间的速度与加速度连续。 根 据以上条件，推导出求解未知系数 aji 与插值点的关系式（４）唱 （７）。 式（４）中的 t１、t２、t３ 表示第 j 段关节的３ 段多项式插值的 时间。 式（６）即是系数 aji的解。 ０ ０ ０ －２ t２２ t３２ ３t２２ ２t２ ２ ６t２ ０ ０ ０ ０ ０ ０ ０ ０ ０ ０ ０ ０ ０ ０ ０ ０ ０ ０ ０ ０ ０ ０ －２ t２３ t３３ ３t２３ ２t３ ６t３ ２ ０ ０ ０ ０ ０ ０ ０ ０ ０ ０ ０ ０ ０ ０ ０ －１ ０ t３ １ ０ ０ ０ ０ ０ ０ ０ ０ ０ ０ ０ ０ ０ －１ ０ ０ １ ０ ０ ０ ０ ０ １ ０ ０ －１ ０ ０ １ ０ ０ ０ ０ ０ ０ ０ ０ ０ １ ０ ０ ０ ０ －１ ０ ０ t４２ t２ ４t３２ １ １２t２２ ０ ０ ０ ０ ０ ０ ０ ０ ０ ０ ０ ０ ０ ０ ０ ０ ０ a ＝ｉｖn（A） ×b b ＝［０　０　０　０　０　０　Xj３　０　０　Xj０　０　０　Xj２　Xj１］Ｔ （５） （６） ０ ０ ０ t５２ ５t４２ ２０t３２ ０ ０ ０ ０ ０ ０ ０ ０ t３１ ３t２１ ６t１ ０ ０ ０ ０ ０ ０ ０ ０ ０ ０ ０ t２１ ２t１ ２ ０ ０ ０ ０ ０ ０ ０ ０ １ ０ ０ a ＝［aj１３　aj１２　aj１１　aj１０　aj２５　aj２４　aj２３　aj２２　 t１ １ ０ ０ ０ ０ ０ ０ ０ ０ １ ０ ０ ０ １ ０ ０ ０ ０ ０ ０ ０ ０ １ ０ ０ ０ ０ A ＝ （４） aj２１　aj２０　aj３３　aj３２　aj３１　aj３０］ Ｔ （７） t，k） ＝uk ＋vk －uk t ｆｉｔ（t） ＝－f（t） 第 ２８ 卷 （１１） 具体步骤如下： ａ）初始化种群。 对第 j 个关节的三段插值函数时间的搜 索空间中分别随机产生 M 个 l 位二进制串基因码组成的种群， 构成种群 ＰＯＰｔ１、ＰＯＰｔ２、ＰＯＴｔ３。 假设 xi t 是 ml 维的行向量，表 示第 t 代的第 i 个个体。 其中，i∈｛１，２，…，M｝。 每个个体用 l 位二进制表示。 个体 xi t 的第 k 个长度为 l 的二进制编码串转 换为实数的解码函数 Γ为 Γ（xi ×２ n －１） n ＝１xl（kl ＋n） （１２） ２ l －１ （ ∑l 其中：vk、uk 分别表示为第 k 个实数范围的上限和下限。 随机 产生基因码的值，并计算相应的实数。 ｂ）根据产生的 M 组 ３唱５唱３ 多项式插值时间组合，代入式 （４）（７），求解出 aji的系数矩阵 a。 ｃ）将系数矩阵 a 代入式（１）（３）求解出三段多项式。 多项 式对时间求导，得到三段多项式的速度函数。 判断多项式的最 大速度是否符合式（９）。 ｄ）适应度函数的构建有两个任务：首先使机械臂运动速 度收敛到运动学约束内；然后使各段插值时间尽量减小。 对 ｃ）的计算结果采用两个适应度函数切换的开关控制，即如果 三段中的任一速度函数不符合式（９），该段的目标函数为｜v（j， i）｜。 如果三段的速度全部满足式（９） 的约束，则目标函数切 换为 ｍｉｎ （tji），以减小每段关节运行时间为优化目标进行迭 代。 其中 j 为 M 组种群的第 j 组，i 为多项式插值的段数，取值 范围是１、２、３。 如果有的个体不满足其运动学约束，在下一步 中，该个体被淘汰的几率会增加。 ｅ）自适应遗传操作： （ａ）选择。 一般遗传算法中采用的选择方式为轮盘赌选 择机制，其最大的缺点是容易导致进化过程中出现过早收敛和 停滞。 为了解决这个问题，ＡＧＡ 采用优胜劣汰选择策略。 将 适应度函数按升序排列，每次随机地从种群中挑选一定数目的 个体，并将其中最好的选做父个体。 （ｂ）交叉和变异。 通过计算种群的平均适应度 fａｖｇ 与种群 最优适应度 fｍａｘ之间的关系来判别遗传算法是否收敛于最优： 当最优解的适应度与平均适应度接近，即｜fｍａｘ －fａｖｇ｜变小时，种 群收敛于最优解的可能性大于种群发散在解空间的可能性；反 之亦然。 Pc 和 Pm 值依赖于｜fｍａｘ －fａｖｇ ｜的变化，当整个种群趋 于收敛时，增大 Pc 和 Pm 值，反之减小。 为了得到好的效果， 既要避免算法收敛于局部最优，也要防止优良基因受到破坏， 因此适应度较优的个体应有较小的 Pc 和 Pm 值，而适应度较劣 ［８］。 这样提高了群体中表现优 的个体应有较大的 Pc 和 Pm 值 良的个体的交叉率和变异率，使它们不会处于一种近似停滞不 前的状态。 自适应交叉率和变异率为 ［９］： Pc ＝ Pc１ －（Pc１ －Pc２）（f ′－fａｖｇ） fｍａｘ －fａｖｇ Pm ＝ Pm１ －（Pm１ －Pm２）（fｍａｘ －f） 　f ′≥fａｖｇ Pc１　　　　　　　　　　　f ′≥fａｖｇ 　f≥fａｖｇ Pm１　　　　　　　　　　　f≥fａｖｇ （１４） 其中：f′ 是要交叉的两个个体中较大的适应度值，f 为要变异个 体的适应度值。 为了保证每一代的优良个体不被破坏，采用精 英选择策略，选择适应度最优的个体，直接复制到下一代中。 上式中 Pc１ ＝０．９，Pc２ ＝０．４，Pm１ ＝０．１，Pm２ ＝０．０１。 ｆ）构成新的 M ×３ 种群 ＰＯＰｔ１、ＰＯＰｔ２、ＰＯＰｔ３。 fｍａｘ －fａｖｇ （１３） 2　时间最优问题求解 式（４）（７）对３唱５唱３ 多项式未知系数的解算是以每段多项 式插值时间已知为基础的。 如何选择最优的时间，使机械臂在 最短的时间内完成运动且满足速度约束，是本文研究的主要内 容。 优化目标是满足运动学约束的所有关节的运动时间最短。 其函数为 （８） 函数为 j ＝０tj１ ＋tj２ ＋tj３ f（t） ＝ｍｉｎ∑n ｍａｘ｛ ｜Vj３ ｜｝≤Vｍａｘ j ＝１，２，３，４，n ｓ．ｔ．ｍａｘ｛ ｜Vj１ ｜｝≤Vｍａｘ，ｍａｘ｛ ｜Vj２ ｜｝≤Vｍａｘ f（t） ＝ｍｉｎ（tj１ ＋tj２ ＋tj３） （９） 式（８）中：Vj１、Vj２、Vj３ 是第 j 个关节每段多项式随时间变化的速 度。 对机械臂每个关节单独进行优化。 第 j 个关节优化目标 （１０） ３唱５唱３ 多项式插值函数应用粒子群算法，如何选择自变量 id是关键问题。 式（４）（７） 中 以确定因变量 xk 时间 t１、t２、t３ 是待优化的未知量，系数 aji 也是待求解的未知 数。 如果把未知系数 aji当做自变量，t１、t２、t３ 当做因变量，待优 化的变量维数为１４，计算量大且复杂。 本文直接在待优化时 间 t１、t２、t３ 的搜索空间里优化，搜索维数降低为３ 维，避免了推 导复杂的映射关系。 t１、t２、t３ 是未知量，其搜索空间需要根据 经验设定在尽可能大的范围。 为了使关节运动速度尽快收敛 到约束内，采用两种适应度函数的开关控制。 在满足运动学约 束后，进行时间最优的自适应遗传算法优化迭代。 id，并选择出最佳 xk 适应度函数取目标函数的负数为 

付　荣，等：基于 ＡＧＡ 的时间最优机械臂轨迹规划算法 间的最大值，以确保满足运动学约束。 第 ９ 期 ｇ）满足终止条件则算法结束，否则转 ｂ）。 ｈ）完成所有关节的时间优化。 每段时间取各关节该段时 t１ ＝ｍａｘ｛tj１｝；t２ ＝ｍａｘ｛tj２｝；t３ ＝ｍａｘ｛tj３｝　j ＝１，２，３，４，n 遗传算法需要循环迭代。 本文研究的遗传算法是在优化 目标的搜索空间内搜索，在计算式（４）时，如果迭代步数很大， 易造成矩阵不满秩，这影响了该方法在复杂目标优化的应用， 所以在每一步迭代过程中，都要检验新产生种群是否有实数值 为０ 的个体。 如果有，则要重新随机产生该个体的值。 3　仿真与实验结果 本文研究 Ｂ２ 型月球车上驱动相机盒运动的六自由度正 交解耦机械臂，整体结构如图１ 所示。 机械臂腕心位置即相机 盒位置。 关节１ ～３ 旋转方向两两正交，解耦于控制相机盒定 向的关节４ ～６，如图２ 所示。 ·７７２３· 　　　 个体。 二进制解码为实数的上下限０２．５５ ｓ。 遗传算法迭代时 间为５０ 步。 关节允许的最大运动速度是 Vｍａｘ ＝３ ｍ／ｓ。 初始 和终点的速度与加速度都是０。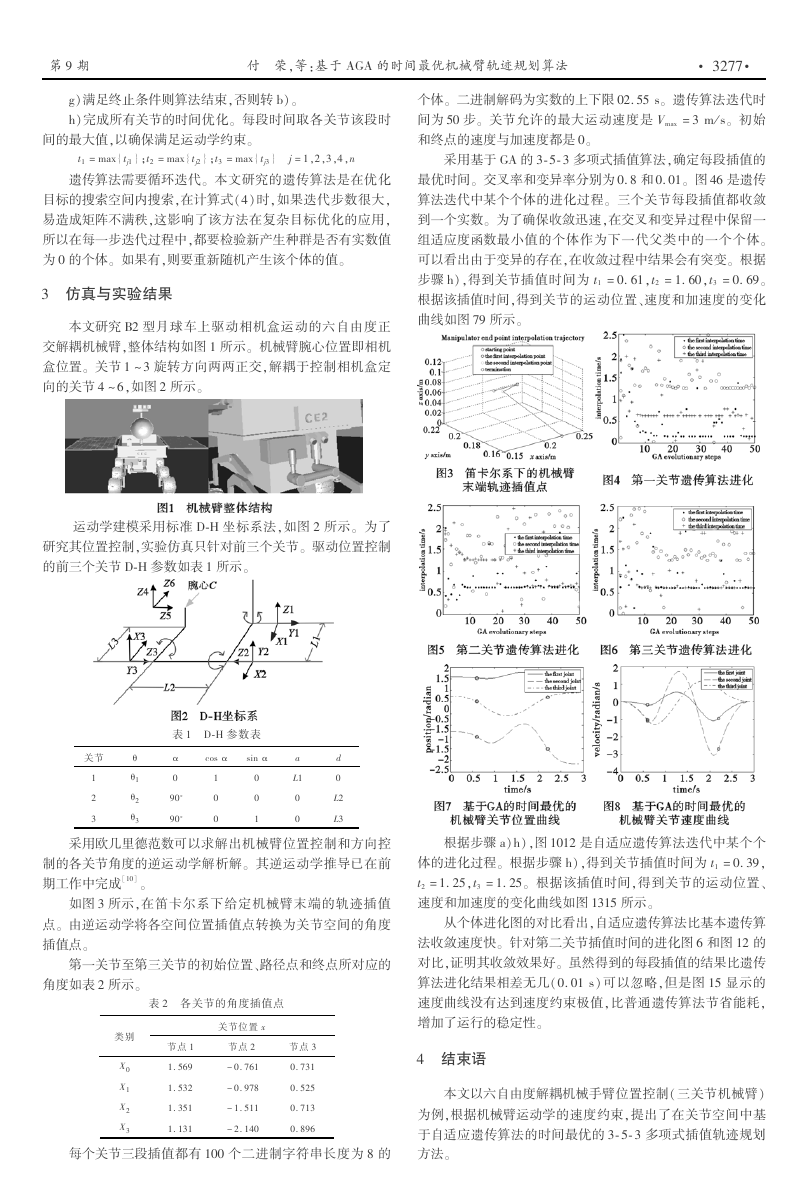 采用基于 ＧＡ 的３唱５唱３ 多项式插值算法，确定每段插值的 最优时间。 交叉率和变异率分别为０．８ 和０．０１。 图４６ 是遗传 算法迭代中某个个体的进化过程。 三个关节每段插值都收敛 到一个实数。 为了确保收敛迅速，在交叉和变异过程中保留一 组适应度函数最小值的个体作为下一代父类中的一个个体。 可以看出由于变异的存在，在收敛过程中结果会有突变。 根据 步骤 ｈ），得到关节插值时间为 t１ ＝０．６１，t２ ＝１．６０，t３ ＝０．６９。 根据该插值时间，得到关节的运动位置、速度和加速度的变化 曲线如图７９ 所示。 运动学建模采用标准 Ｄ唱Ｈ 坐标系法，如图２ 所示。 为了 研究其位置控制，实验仿真只针对前三个关节。 驱动位置控制 的前三个关节 Ｄ唱Ｈ 参数如表１ 所示。 关节 １ ２ ３ θ θ１ θ２ θ３ 表 １　Ｄ唱Ｈ 参数表 ｃｏｓ α ｓｉｎ α α ０ ０ １ ０ ０ ９０闭 ９０闭 ０ １ a L１ ０ ０ d ０ L２ L３ ［１０］。 期工作中完成 　　采用欧几里德范数可以求解出机械臂位置控制和方向控 制的各关节角度的逆运动学解析解。 其逆运动学推导已在前 如图３ 所示，在笛卡尔系下给定机械臂末端的轨迹插值 点。 由逆运动学将各空间位置插值点转换为关节空间的角度 插值点。 第一关节至第三关节的初始位置、路径点和终点所对应的 角度如表２ 所示。 表 ２　各关节的角度插值点 类别 X０ X１ X２ X３ 节点 １ ．５６９ １ ．５３２ １ １ ．３５１ ．１３１ １ 关节位置 x 节点 ２ ．７６１ －０ ．９７８ －０ －１ ．５１１ ．１４０ －２ 节点 ３ ．７３１ ０ ．５２５ ０ ０ ．７１３ ．８９６ ０ 　　每个关节三段插值都有１００ 个二进制字符串长度为 ８ 的 根据步骤 ａ）ｈ），图１０１２ 是自适应遗传算法迭代中某个个 体的进化过程。 根据步骤 ｈ），得到关节插值时间为 t１ ＝０．３９， t２ ＝１．２５，t３ ＝１．２５。 根据该插值时间，得到关节的运动位置、 速度和加速度的变化曲线如图１３１５ 所示。 从个体进化图的对比看出，自适应遗传算法比基本遗传算 法收敛速度快。 针对第二关节插值时间的进化图６ 和图１２ 的 对比，证明其收敛效果好。 虽然得到的每段插值的结果比遗传 算法进化结果相差无几（０．０１ ｓ） 可以忽略，但是图 １５ 显示的 速度曲线没有达到速度约束极值，比普通遗传算法节省能耗， 增加了运行的稳定性。 4　结束语 本文以六自由度解耦机械手臂位置控制（三关节机械臂） 为例，根据机械臂运动学的速度约束，提出了在关节空间中基 于自适应遗传算法的时间最优的３唱５唱３ 多项式插值轨迹规划 方法。 

·８７２３· 计 算 机 应 用 研 究 　 第 ２８ 卷 　　Pc 和 Pm 参数的选择对遗传算法的寻优性能影响很大。 普通遗传算法在进化过程中采用固定的 Pc、Pm 值使收敛速度 慢，容易陷入早熟收敛；自适应遗传算法根据适应度的分散程 度自适应改变 Pc、Pm，明显改善了遗传算法的搜索性能。 本文 核心是利用自适应遗传算法优化多项式插值时间，通过与普通 遗传算法进化过程作对比，可以看出自适应遗传算法比普通遗 传算法提高了收敛速度，并使后者减少趋于局域最优解的情 况。 实验证明，两个算法虽然在优化上都使在满足运动学约束 的条件下性能达到优化，但自适应遗传算法的优化不仅避免了 遗传算法存在的收敛速度慢和早熟收敛等问题，还减小了机械 臂运动能耗，增加了运行平稳性。 参考文献： ［１］ ＳＲＩＮＩＶＡＳ Ｍ， ＰＡＴＮＡ ＩＫ Ｌ Ｍ．Ａｄａｐｔｉｖｅ ｐｒｏｂａｂｉｌｉｔｉｅｓ ｏｆ ｃｒｏｓｓｏｖｅｒ ａｎｄ ｍｕｔａｔｉｏｎ ｉｎ ｇｅｎｅｔｉｃ ａｌｇｏｒｉｔｈｍ［Ｊ］．IEEE Trans on Systems， Man and Cybernetics，１９９４，24（４）：６５６唱６６７． ［２］ 刘智明，贺新．基于排序的改进自适应遗传算法［Ｊ］．信息与控制， ２００４，33（１）：６唱８． ［３］ 石山，励庆孚，王兴华．基于自适应遗传算法的无刷直流电机的优 化设计［Ｊ］．西安交通大学学报，２００２，36（１２）：１２１５唱１２１８． ［４］ 喻寿益， 邝 溯 琼．嵌 套 式 模 糊 自 适 应 遗 传 算 法［Ｊ］．控 制 工 程， ２０１０，17（１）：７５唱７９． ［５］ 恽为民，戴先中，席裕庚．基于遗传算法的多机器人关节空间最优 运动规划［Ｊ］．机器人，１９９７，17（４）：２０６唱２１７． ［６］ 甘亚辉，戴先中．基于遗传算法的多机器人系统的最优轨迹规划 ［Ｊ］．控制理论与应用，２０１０，27（９）：１２４５唱１２５１． ［７］ 张勇，张宪民，胡峻峰，等．高速并联机械手最优时间轨迹规划及 实现［Ｊ］．机电工程技术，２０１０，39（１０）：４２唱４５． ［８］ 周小燕，高峰，鲍官军，等．基 于 ＩＡＧＡ 的 机 械 手 时 间 最 优 轨 迹 规 划［Ｊ］．机电工程，２００９，26（８）：１唱３． ［９］ 王小平，曹立明．遗传算法理论应用与软件实现［Ｍ］．西安：西安 交通大学出版社，２００２：１唱１０１． ［１０］ 付荣，居鹤华．高精度解耦六自由度机械臂逆运动学解法［Ｊ］．计 算机测量与控制，２０１０，18（７）：１６３７唱１６４０． ［１１］ 刘超，欧杰，曹祺．基 于 自 适 应 遗 传 算 法 的 航 迹 规 划 研 究［Ｊ］．飞 行力学，２０１０，28（１）：３６唱３９． 本文根据多起重机共直流母线节能系统的结构及组成特 （ 上接第 ３２７４ 页） 5　结束语 点，构建了系统形式化模型及等效电路；利用混杂系统理论，逐 一建立等效电路中各单元电路模型，进而得到系统整体模型。 仿真研究了系统直流母线的功率和电压，验证了所建模型的合 理性，提出了通过协调调度起重机状态提高节能效果，保证系 统可靠运行的新方法，为更好地开展多起重机协调调度节能控 制算法的研究提供了仿真模型。 参考文献： ［１］ 王万新．公共直流母线在交流传动中的应用［Ｊ］．电气传动，２００２， 32（５）：５７唱５８． ［２］ 王云飞，杨耕．通用变频器—感应起重机系统的起重机耗能型制 动控制方法［Ｊ］．电工技术学报， ２００６，21（１）：８７唱９２． ［３］ 刘永峰，谢 吉 华．变 频 器 回 馈 制 动 研 究［Ｊ］．变 频 器 世 界，２００８ （８）：５２唱５４． ［４］ ＧＯＥＢＥＬ Ｒ， ＳＡＮＦＥＬＩＣＥ Ｒ Ｇ， ＴＥＥＬ Ａ Ｒ．Ｈｙｂｒｉｄ ｄｙｎａｍｉｃａｌ ｓｙｓ唱 ｔｅｍｓ［Ｊ］．IEEE Control Systems Magazine，２００９（４）： ２８唱９３． ［５］ 侯媛彬， 李倩．基于 Ｐｅｔｒｉ 网分解技术的自动化物流系统建模分 析［Ｊ］．计算机应用研究， ２０１０，27（１１）：４１３３唱４１３５． ２００４，16（３）：３７５唱３８０． 真［Ｊ］．系统仿真学报，２００８，20（１０）：２７４０唱２７４５． 策略［Ｊ］．计算机应用研究， ２０１０，27（９）：３２９０唱３２９３． ［Ｊ］．系统仿真学报，２０１０，22（４）：８３３唱８３６． 制［Ｊ］．动力工程，２００９，29（４）：３６９唱３７５． 真［Ｊ］．系统仿真学报，２００７，19（１５）：３５４６唱３５４９． 计算机应用研究， ２０１０，27（１）：１９６唱１９９． 21（３）：７６唱８１． ［６］ 薛乐，廖 沫， 魏 晨，等．混 合 系 统 及 其 建 模［Ｊ］．系 统 仿 真 学 报， ［７］ 田晓丹，罗飞，许玉格．基于细胞自动机的电梯混合系统建模及仿 ［８］ 赵小翠， 罗飞， 许玉格．混合电梯群控系统建模及新型优化调度 ［９］ 秦琳琳， 石 春， 吴 刚．基 于 混 杂 系 统 的 温 室 天 窗 温 度 系 统 建 模 ［１０］ 徐大平， 高峰， 吕跃刚．基于混杂系统的风力发电机组建模与控 ［１１］ 张悦，王东风，韩璞，等．一类混杂系统的推广自动机模型及其仿 ［１２］ 张萌， 高德远， 樊 晓 桠．基 于 混 合 自 动 机 的 ＰＳＬ 模 型 研 究［Ｊ］． ［１３］ 林健．三阶段法与活动周期图［Ｊ］．北京航空航天大学学报，１９９５， ［１４］ 王维平．离散事件系统建模与仿真［Ｍ］．北京：科学出版社，２００７． ［１５］ ＰＡＵＬ Ｒ Ｊ．Ａｃｔｉｖｉｔｙ ｃｙｃｌｅ ｄｉａｇｒａｍｓ ａｎｄ ｔｈｅ ｔｈｒｅｅ ｐｈａｓｅ ｍｅｔｈｏｄ［Ｃ］ ／／ Ｐｒｏｃ ｏｆ ｔｈｅ ２５ｔｈ Ｃｏｎｆｅｒｅｎｃｅ ｏｎ Ｗｉｎｔｅｒ Ｓｉｍｕｌａｔｉｏｎ．１９９３：１２３唱１３１． ［１６］ ＭＡＲＴＩＮＥＺ Ｊ Ｃ．ＥＺＳｔｒｏｂｅ唱ｇｅｎｅｒａｌ唱ｐｕｒｐｏｓｅ ｓｉｍｕｌａｔｉｏｎ ｓｙｓｔｅｍ ｂａｓｅｄ ｏｎ ａｃｔｉｖｉｔｙ ｃｙｃｌｅ ｄｉａｇｒａｍｓ［Ｃ］ ／／Ｐｒｏｃ ｏｆ Ｗｉｎｔｅｒ Ｓｉｍｕｌａｔｉｏｎ Ｃｏｎｆｅｒｅｎｃｅ Ｐｒｏｃｅｅｄｉｎｇｓ．２００１： １５５６唱１５６４． ［１７］ Ｄｅ ＬＡＲＡ Ａ Ｆ Ｗ， ＨＩＲＡＴＡ Ｃ Ｍ．Ｔｒａｎｓｌａｔｉｎｇ ａｃｔｉｖｉｔｙ ｃｙｃｌｅ ｄｉａｇｒａｍｓ ｔｏ Ｊａｖａ ｓｉｍｕｌａｔｉｏｎ ｐｒｏｇｒａｍｓ［Ｃ］ ／／Ｐｒｏｃ ｏｆ ｔｈｅ ３７ｔｈ ＩＥＥＥ Ａｎｎｕａｌ Ｓｙｍ唱 ｐｏｓｉｕｍ ｏｎ Ｓｉｍｕｌａｔｉｏｎ．２００４：１５７唱１６４．