第1页 / 共6页
第2页 / 共6页
第3页 / 共6页
第4页 / 共6页
第5页 / 共6页
第6页 / 共6页
论文研究-时滞切换系统指数稳定性分析：Lyapunov-Krasovskii泛函方法.pdf
2
2
2007 年 7 月
文章编号 :1000
系统工程理论与实践
第 7 期
0111
05
6788 (2007) 07
时滞切换系统指数稳定性分析 :Lyapunov
Krasovskii 泛函方法
(1
南京理工大学自动化学院 , 南京 210094 ; 2
东南大学自动化研究所 , 南京 210096)
丛 1 , 费树岷2 , 李 涛2
摘要 : 考虑由两个线性时滞子系统构成的切换系统 ,分析其在任意切换序列作用下保持指数稳定性的
条件. 分别利用二次型与逐段二次型的 Lyapunov
Krasovskii 泛函构造方式给出了以线性矩阵不等式所表
述的稳定性判据 ;进而通过状态变量代换结合积分不等式技巧证明了指数衰减率对于所有切换序列一
致成立 ,即其完全取决于系统的结构特征. 最后给出了一个算例.
关键词 : 切换系统 ; 时滞 ; 指数稳定 ; Lyapunov
Krasovskii 泛函
中图分类号 : TP27 文献标志码 : A
On Exponential Stability of Switched Systems with Delay :
Lyapunov
Krasovskii Functional Approach
Department of Automation , Nanjing University of Science and Technology , Nanjing 210094 , China ; 2
(1
Automation , Southeast University , Nanjing 210096 , China)
Research Institute of
CONG Shen1 , FEI Shu
min2 , LI Tao2
Abstract : We consider switched dynamical systems consisting of two linear subsystems with delay. The problem is to
find conditions guaranteeing exponential stability of the system for any switching sequence. Both quadratic and
piecewise quadratic construction of Lyapunov
Krasovskii functional is exploited , from which the stability criteria in
terms of linear matrix inequalities are derived. Furthermore , based on the state transformation combining with integral
inequality technique , it is strictly verified that the exponential decay rate holds uniformly for all switching sequence ,
and is definitely determined by the structure of subsystems. Numerical examples are given to demonstrate the
effectiveness of our results.
Key words : switched systems ; time
delay ; exponential stability ; Lyapunov
Krasovskii functional
1 引言
本文的研究对象是由两个具有时不变系数矩阵的时滞线性子系统 :
x ( t) = Ai x ( t) + Ai1 x ( t -
r) , t ≥ t0 , i = 1 ,2
(1
a)
在取值于指标集{1 ,2}的右连续切换信号 :
s ∶=
( t0 ,π(0) ) , …( tk ,π( k) ) , …|
tk = ∞
lim
k →∞
驱动下构成的切换系统. 其中 x ∈R n , r > 0 为状态变量与时滞常数 ,{ Ai , Ai1 }2
π( k) 为切换时刻及相应的切换序列取值.
(1
i = 1 为适当维数矩阵 ;
b)
tk ,
时滞与切换是自然现象的理想化数学描述 ,二者相互耦合可能导致复杂的系统动力学行为. 如果给定
切换序列 (2) ,时滞切换系统 (1) 成为具有非连续时变系数矩阵的自治系统 ,著作[ 1 ]证明了其解的整体存
在唯一性 ,并且其一致渐近稳定性等价于指数稳定性. 对于具有非时变系数矩阵的时滞系统 ,为导出与时
滞相关的稳定性判据 ,在 Lyapunov
Krasovskii 泛函的构造中通常包含了时间的“平移”变换[2 ] 或状态导
数[3 ] ;由于切换系统的时变性与非连续性 ,前者变换效应的积累将导致稳定性分析失去因果性 ,而后者将
收稿日期 :2006
资助项目 :国家自然科学基金 (60574006)
22
05
作者简介 :丛 (1976 - ) , 男 , 黑龙江哈尔滨人 , 博士 , 研究方向 : 切换系统与时滞系统的分析与综合.
Π
211
系统工程理论与实践
导致泛函失去连续性这一基本前提.
2007 年 7 月
非二次型 Lyapunov 函数[4 ] 与多 Lyapunov 函数[5 ] 方法是切换系统稳定性分析中具有代表性的成果 ,前
者构建于有限维欧式空间中不变集的几何结构 ,而后者根植于不同 Lyapunov 函数在有限维欧式空间上的
几何相容性 ①;在时滞条件下 ,相空间为无穷维函数空间 ,因此这些方法的适用条件不再成立. 时滞现象的
存在丰富了切换系统稳定性问题的理论体系 ;但是在其方法与结论推广中存在根本的局限性与保守性. 文
献[6 ,7 ]分别基于 Lyapunov
Razumikhin 函数方法将[8 ]中关于度量空间上非连续
混杂动力系统稳定性分析的若干充分性结论推广至时滞情形. 文献[ 9 ]考虑了时滞切换系统的镇定问题 ,
其方法没有突破二次镇定的研究模式.
Krasovskii 泛函与 Lyapunov
切换系统的时变性与非连续性取决于切换序列的行为 ,这是其区别于一般时变系统的特殊性所在. 本
文从泛函微分方程稳定性的原始论证方式入手 ,分别利用二次型与逐段二次型 Lyapunov
Krasovskii 泛函方
法分析系统 (1) 在任意切换序列作用下保持一致渐近稳定的条件 ;进而证明了其指数衰减率对于所有切换
序列一致成立 ,即完全由子系统属性所确定. 在无时滞条件下这是近乎显然的结论[10 ] ,也是切换系统区别
于一般时变系统的重要特征.
2 记号与引理
Cn ,r∶= C ( [ - r ,0 ] , R n ) , r > 0 表示由[ - r ,0 ]映入 R n 的具有一致范数的连续函数构成的 Banach 空
, ‖·‖分别表示 R n , Cn , r上的度量. 对于实对称矩
间 , xt ∈Cn , r含义为 xt (θ) = x ( t +θ) ,θ∈[ - r ,0 ] ;| ·|
阵 ,λmax (·) ,λmin (·) 分别表示其最大与最小特征值. D + 为实值连续函数的右导数算子.
设可测向量值函数集合 M∶= [ m1 ( t) , m2 ( t) ]′ ∑
mi ( t) ≡1 , mi ( t) ≥0 ; i = 1 ,2 . 根据非连续系统的
2
i = 1
描述方法[9 ] ,对于任意切换序列 ,系统 (1) 等价地转化为微分包含的形式 :
其中 F( xt ) ∶= co{ Ai x ( t) + Ai1 x ( t - r) | i = 1 ,2}. 下述等价性条件[11 ] 反映了切换系统的时变本质.
x ( t) ∈ F( xt ) , t ≥ t0
(2)
引理 1 记 珔A i ∶= A i + Ai1 , i = 1 ,2. 对于所有[ m1 ( t) , m2 ( t) ]′∈M ,微分包含 (2) 与下列泛函微分方程 :
(3)
x ( t) = A ( t) x ( t) + A1 ( t) x ( t -
r) = 珔A ( t) x ( t) + A1 ( t) zt ( -
r) , t ≥ t0
解的集合是一致的. 其中 A ( t) = ∑
xt (0) , - r ≤θ≤0 满足 zt (0) ≡0 , t ≥t0 .
i = 1
2
mi ( t) Ai , A1 ( t) = ∑
mi ( t) Ai1 ,珔A ( t) = ∑
mi ( t)珔A i ; zt (θ) ∶= xt (θ) -
2
i = 1
2
i = 1
引理 2 (S
1) G( x) < 0 ;
procedure[12 ] ) 设 G( x) , H( x) , x ∈R n 为二次型函数 ,那么下列命题相互等价 :
x ∈R n .
x ∈{ y ∈R n | H( y) ≤0} ; 2) 存在 λ≥0 ,使得 G( x) - λH( x) ≤0 ,
3 主要结论
子系统的稳定性是系统 (1) 在任意切换作用下保持稳定的必要条件. 时滞系统的稳定判据相当丰富 ,
其保守性也不尽相同. 分析切换系统的稳定性 ,须突出时变本质 ,忽略子系统稳定性判据之间的异性 ,提取
其共性加以描述与分析 ,这是本文方法与结论的基本出发点.
3
Krasovskii 泛函分析方法
1 二次型 Lyapunov
定理 1 如果存在对称矩阵 P , Q > 0 满足下述线性矩阵不等式 :
珔A′i P + P珔A i
rA′i1 P
rPAi1
-
rQ
< 0 , i = 1 ,2
(4)
那么存在常数κ≥1 , v > 0 使得对于任意切换序列与给定初始条件 ,时滞切换系统 (1) 的解是指数衰减的 ,
并满足| x ( t) | ≤κ‖xt
‖e - v ( t - t
, t ≥t0 .
0
)
0
① 拓扑空间{Ω ,τ}上非负连续实值函数 u , v 具有几何相容性 ,如果存在 0 <α<β,使得αv ( w) ≤u ( w) ≤βv ( w) ,
w ∈Ω.
1
第 7 期
时滞切换系统指数稳定性分析 :Lyapunov
Krasovskii 泛函方法
311
证明 根据引理 1 ,只要证明泛函微分方程 (3) 的指数稳定性即可. 依据 Schur 补引理及不等式 (4) 的
线性与严格性可知 ,存在 0 < l < 1 ,使得下列 Riccati 不等式成立 :
2
i = 1
2
i = 1
∑
mi珔A′i P + P ∑
mi珔A i + rP ∑
miA i1 Q - 1 ∑
miA′i1 P + (1 -
2
i = 1
2
i = 1
其中 m1 + m2 = 1 ,0 ≤m1 , m2 ≤1.
构造如下状态变换 :
ξ( t) ∶=
r ≤ t ≤ t0
x ( t) , t0 -
1
2
( t - t
0
e
) x ( t) , t ≥ t0
得到
ξ( t) = e
1
2
( t - t
)
0
1
2 x ( t) +
x ( t)
, t ≥t0 . 泛函微分方程 (3) 变换为 :
ξ( t) = 珔A ( t) +
1
2 In ξ( t) + A1 ( t)ηt ( -
r) , t ≥ t0
其中 ηt (θ) ∶= e
- 1
2
θξt (θ) - ξt (0) ,θ∈[ - r ,0 ] , t ≥t0 ,满足 ηt (0) ≡0 , t ≥t0 .
l) P < 0
(5)
(6)
(7)
构造如下 Lyapunov
Krasovskii 泛函 V (ξt ) = rξ′( t) Pξ( t) +∫
η′t (θ) Qηt (θ) dθ, t ≥t0 . 依据 (5) 可知 ,其
0
- r
沿着方程 (7) 解轨线的导数满足 :
D + V (ξt ) = 2 r[ (珔A ( t) +
1
2 In )ξ( t) + A1 ( t)ηt ( -
r) ]′Pξ( t) - η′t ( -
r) Qηt ( -
r)
≤ξ′( t) [ r珔A′( t) P + rP珔A ( t) + r2 PA1 ( t) Q - 1 A′1 ( t) P + rP]ξ( t) ≤ rlξ′( t) Pξ( t) , t ≥ t0
(8)
设 w ( t) ∶= rξ′( t) Pξ( t) = rx′( t) Px ( t) exp ( t - t0 ) , t ≥t0 ,由 (8) 推知 :
w ( t) ≤V (ξt ) ≤V (ξt
0
D + V (ξτ) dτ ≤V (ξt
w (τ) dτ, t ≥ t0
) +∫
t
t
0
) + l∫
0
t
t
0
由此根据 Gronwall [1 ] 不等式可知 :
) exp [ l ( t -
w ( t) ≤V (ξt
0
结合 ( 6 , 9) 得 到 , | x ( t ) | ≤κ ‖ xt
‖ e - v ( t - t
0
)
0
λmax ( P) +λmax ( Q)
λmin ( P)
1
2
, v =
1 - l
2
> 0. □
t0 ) ] ≤ r[λmar ( P) + λmax ( Q) ] ‖xt
(9)
, t ≥ t0 在 任 意 切 换 序 列 作 用 下 成 立 , 其 中 κ =
‖2exp [ l ( t -
t0 ) ] , t ≥ t0
0
定理 1 的结论可以推广至任意有限子系统 ,下述分析过程则只适用于两个子系统的情形.
3
2 逐段二次型 Lyapunov
Krasovskii 泛函分析方法及其求解
定性问题 ,缺少非二次型 Lyapunov
方式 ,结合 S
有限维欧氏空间中不变集的几何结构刻画了非二次型 Lyapunov 函数的构造[13 ] . 对于泛函微分方程稳
Krasovskii 泛函的一般性构造方法. 下文中利用逐段二次型的泛函构造
procedure 引理推证了时滞切换系统在任意切换序列作用下的指数稳定性判据.
定理 2 如果存在λ1 ,λ2 ,λ3 ,λ4 ≥0 ,使得下列关于对称矩阵 P1 , P2 , Q > 0 的线性矩阵不等式可解 :
珔A′1 P1 + P1珔A 1 - λ1 ( P2 - P1 )
珔A′2 P1 + P1珔A 2 - λ2 ( P2 - P1 )
rA′11 P1
珔A′1 P2 + P2珔A 1 + λ3 ( P2 - P1 )
rA′11 P2
rP1 A11
-
rQ
< 0 ,
rP2 A11
-
rQ
< 0 ,
rA′21 P1
珔A′2 P2 + P2珔A 2 + λ4 ( P2 - P1 )
rA′21 P2
rP1 A21
-
rQ
< 0 (10
a ,b)
rP2 A21
-
rQ
< 0 (10
c ,d)
那么存在κ> 1 , v > 0 ,使得对于任意切换序列与给定初始条件 ,时滞切换系统 (1) 的解是指数衰减的 ,并满
足| x ( t) | ≤κ‖xt
‖e - v ( t - t
, t ≥t0 .
0
)
0
证明 依据 Schur 补引理及不等式 (10) 的线性与严格性可知 ,存在 0 < l < 1 ,使得下列 Riccati 不等式
成立 :
1
1
411
系统工程理论与实践
2007 年 7 月
珔A′1 P1 + P1珔A 1 + rP1 A11 Q - 1 A′11 P1 - λ1 ( P2 - P1 ) < -
珔A′2 P1 + P1珔A 2 + rP1 A21 Q - 1 A′21 P1 - λ2 ( P2 - P1 ) < -
珔A′1 P2 + P2珔A 1 + rP2 A11 Q - 1 A′11 P2 + λ3 ( P2 - P1 ) < -
珔A′2 P2 + P2珔A 2 + rP2 A21 Q - 1 A′21 P2 + λ4 ( P2 - P1 ) < -
(1 -
l) P1
(1 -
(1 -
l) P1
l) P2
(1 -
l) P2
(11
(11
(12
(12
a)
b)
a)
b)
应用引理 3 推知不等式 (11 ,12) 分别等价于下述命题 :
1) 若 x′P1 x ≥x′P2 x ,则
x′ ∑
mi珔A′1 P1 + P1 ∑
mi珔A i + rP1 ∑
miAi1 Q - 1 ∑
miA′i1 P1
2) 若 x′P1 x ≤x′P2 x ,则
x′ ∑
mi珔A′1 P2 + P2 ∑
mi珔A i + rP2 ∑
miAi1 Q - 1 ∑
miA′i1 P2
i = 1
2
2
i = 1
i = 1
2
2
i = 1
i = 1
2
2
i = 1
i = 1
2
2
i = 1
x < -
(1 -
l) x′P1 x
(13
a)
x < -
(1 -
l) x′P2 x
(13
b)
其中 0 ≤m1 , m2 ≤1 , m1 + m2 = 1.
构 造 逐 段 二 次 Lyapunov
Krasovskii 泛 函 V (ξt )
=
r max{ξ′( t) P1ξ( t) ,ξ′( t) P2ξ( t) } +
0
∫
η′t (θ) Qηt (θ) dθ, t ≥ t0 . 逐段计算其沿着方程 (7) 解轨线的导数 ,若ξ′( t) P1ξ( t) ≥ξ′( t) P2ξ( t) , t ≥t0 ,
则依据 (13
a) 得到 :
- r
D + V (ξt ) ≤ξ′( t) [ r珔A′( t) P1 + rP1珔A ( t) + r2 P1 A1 ( t) Q - 1 A′1 ( t) P1 + rP1 ]ξ( t) ≤ rlξ′( t) P1ξ( t)
(14
a)
若ξ′( t) P1ξ( t) ≤ξ′( t) P2ξ( t) , t ≥t0 ,则依据 (13
b) 得到 :
D + V (ξt ) ≤ξ′( t) [ r珔A′( t) P2 + rP2珔A ( t) + r2 P2 A1 ( t) Q - 1 A′1 ( t) P2 + rP2 ]ξ( t) ≤ rlξ′( t) P2ξ( t)
(14
b)
0 max{ x′( t) P1 x ( t) , x′( t) P2 x ( t) } , t ≥t0 ,由 (14) 推
设 w ( t) ∶= r max{ξ′( t) P1ξ( t) ,ξ′( t) P2ξ( t) } = ret - t
知 :
w ( t) ≤V (ξt ) ≤V (ξt
0
D + V (ξτ) dτ ≤V (ξt
w (τ) dτ, t ≥ t0
) +∫
t
t0
) + l∫
0
t
t0
记珋λ∶= max{λmax ( P1 ) ,λmax ( P2 ) } ,λ∶= min{λmin ( P1 ) ,λmin ( P2 ) }由此根据 Gronwall 不等式可知 :
t0 ) ] , t ≥ t0
t0 ) ] ≤ r[珋λ + λmax ( Q) ] ‖xt
w ( t) ≤V (ξt
‖2 exp [ l ( t -
) exp [ l ( t -
0
0
(15)
结合 (6 ,15) ,从而得到 :
| x ( t) | ≤κ‖xt
0
‖e - v ( t - t
0
)
, t ≥ t0
在任意切换序列作用下成立 ,其中κ=
珋λ+λmax ( Q)
λ
1
2
, v =
1 - l
2
> 0.
注 1 在定理 2 的结论中 ,适当选取因子参数是其求解的关键 ;下述定理给出了与之等价 ,且便于因
子参数选取的稳定性判据 ,其物理含义也更为清晰.
定理 3 存在λ1 ,λ2 ,λ3 ,λ4 ≥0 与对称矩阵 P1 , P2 , Q > 0 使得线性矩阵不等式 (10) 成立 ,当且仅当存
在 0 <α,β< 1 ,使得下列关于对称矩阵 M1 , M2 , N > 0 的线性矩阵不等式可解 :
珔A′1 M1 + M1珔A 1
rA′11 M1
珔A′2 M2 + M2珔A 2
rA′21 M2
rM1 A11
-
rN
rM2 A21
-
rN
< 0 ,
< 0 ,
α珔A′2 M1 + αM1珔A 2 + (1 - α) ( M1 - M2 ) αrM1 A21
- αrN
β珔A′1 M2 + βM2珔A 1 + (1 - β) ( M2 - M1 ) βrM2 A11
- βrN
αrA′21 M1
βrA′11 M2
< 0 (16
a ,b)
< 0 (16
c ,d)
证明 (充分性) 若λ1 ,λ2 ,λ3 ,λ4 ≥0 , P1 , P2 , Q > 0 是矩阵不等式 (10) 的一组解 ,则不妨设 λ1λ2λ3λ4
> 0 ;根据不等式的严格性 ,通过参数摄动此条件即可满足.
2
2
2
2
第 7 期
时滞切换系统指数稳定性分析 :Lyapunov
Krasovskii 泛函方法
设 γ1 ∶=λ2 +λ4 > 0 ,γ2 ∶=λ1 +λ3 > 0 ,则下述因子与矩阵 :
α∶= (1 + γ1 ) - 1 ,β∶= (1 + γ2 ) - 1
M1 ∶= γ1 (λ1 P2 + λ3 P1 ) , M2 ∶= γ2 (λ2 P2 + λ4 P1 ) , N ∶= γ1γ2 Q
511
(17
(17
a)
b)
即为矩阵不等式 (16) 的一组解.
(必要性) 如果 0 <α,β< 1 与 M1 , M2 , N > 0 为矩阵不等式 (16) 的一组解 ,那么可以验证 λ1 =λ4 = 0 ,λ2 =
α- 1 (1 - α) ,λ3 =β- 1 (1 - β) 与 P1 = M1 , P2 = M2 , Q = N 即满足不等式 (10) .
4 仿真分析
仿真验证定理 1 及定理 2 ,3 的结论. 仿真环境为 Matlab 的 LMI 与 Simulink 工具箱.
- 1
1
, Q =
- 0
0
1
- 0
122
33
33
81
例 1 设 A1 =
- 4
- 6
58
3
007
0
1
- 2
87
96
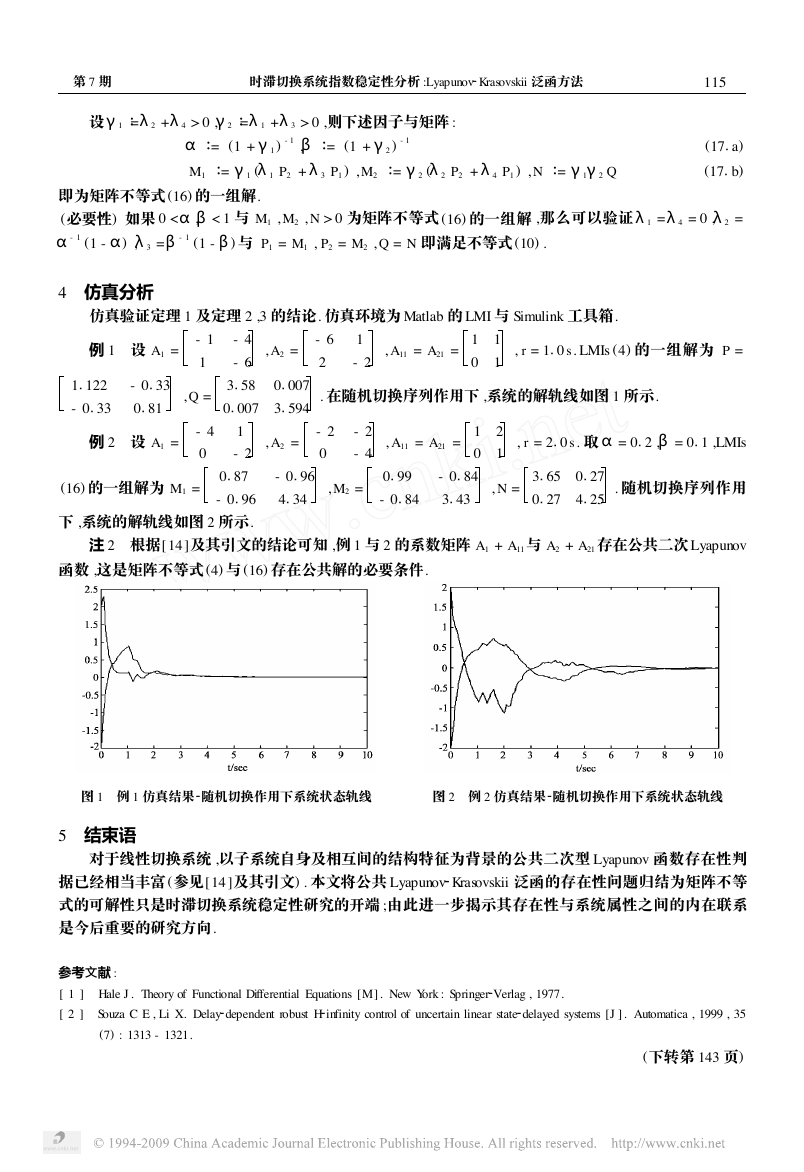
下 ,系统的解轨线如图 2 所示.
(16) 的一组解为 M1 =
例 2 设 A1 =
0
- 0
- 4
0
, A2 =
0
3
007
594
, A2 =
- 6
2
1
- 2
, A11 = A21 =
1
0
1
1
, r = 1
0 s. LMIs (4) 的一组解为 P =
. 在随机切换序列作用下 ,系统的解轨线如图 1 所示.
- 2
0
- 2
- 4
, A11 = A21 =
- 0
4
96
34
, M2 =
0
- 0
99
84
- 0
3
1
0
84
43
2
1
, r = 2
0 s. 取 α= 0
2 ,β= 0
1 ,LMIs
, N =
3
0
65
27
0
4
27
25
. 随机切换序列作用
注 2 根据[14 ]及其引文的结论可知 ,例 1 与 2 的系数矩阵 A1 + A11与 A2 + A21存在公共二次 Lyapunov
函数 ,这是矩阵不等式 (4) 与 (16) 存在公共解的必要条件.
图 1 例 1 仿真结果
随机切换作用下系统状态轨线
图 2 例 2 仿真结果
随机切换作用下系统状态轨线
5 结束语
对于线性切换系统 ,以子系统自身及相互间的结构特征为背景的公共二次型 Lyapunov 函数存在性判
据已经相当丰富 (参见[14 ]及其引文) . 本文将公共 Lyapunov
Krasovskii 泛函的存在性问题归结为矩阵不等
式的可解性只是时滞切换系统稳定性研究的开端 ;由此进一步揭示其存在性与系统属性之间的内在联系
是今后重要的研究方向.
参考文献 :
[ 1 ] Hale J . Theory of Functional Differential Equations [M]. New York : Springer
[ 2 ] Souza C E , Li X. Delay
dependent robust H
infinity control of uncertain linear state
Verlag , 1977.
(7) : 1313 - 1321.
delayed systems [J ]. Automatica , 1999 , 35
(下转第 143 页)
2
第 7 期
环状给水管网优化设计的一种综合方法
341
& Wastewater ,2003 (5) :5 - 7.
[11 ] 吕鉴 ,贾燕兵. 遗传算法在水分配系统优化设计中的应用研究[J ]. 给水排水 ,2001 (2) :36 - 39.
Lv Jian ,Jia Yanbing. Genetic algorithm application of water distribution pipe network systems[J ]. Water & Wastewater Engineering ,
2001 (2) :36 - 39.
[12 ] 严熙世 ,赵洪宾. 给水管网理论和计算[M]. 北京 :中国建筑工业出版社 ,1986.
Yan Xishi , Zhao Hongbin. Tehory and Calculation of Water Distribution Pipe Network [ M ]. Beijing : China Building Industry
Publishing Company ,1986.
[13 ] 白丹. 树状给水管网的优化[J ]. 水利学报 ,1996 , (11) :57 - 67.
Bai Dan. Optimal design of branch distribution pipe network[J ].Journal of Hydraulic Engineering ,1996 , (11) :57 - 67.
[14 ] 茆诗松. 回归分析及其试验设计[M]. 上海 :华东师范大学出版社 ,1986.
Mao Shisong. Regression Analysis and Experimental Design[M]. Shanghai :Shanghai Jiaotong University Publishing Company ,1986.
[15 ] 栾军. 现代试验设计优化方法[M]. 上海 :上海交通大学出版社 ,1995.
Luan Jun. Modern Experimental Design Optimal Method[M]. Shanghai :Shanghai Jiaotong University Publishing Company ,1995.
[16 ] 苏金明. MATLAB6. 1 实用指南[M]. 北京 :电子工业出版社 ,2002.
Su Jinming. MATLAB6. 1 Practicality Manual[M]. Beijing : Electronic Industry Publishing Company ,2002.
(上接第 115 页)
[ 3 ] Fridman E , Shaked U. A descriptor system approach to H
Automatic Control , 2002 , 47 (2) : 253 - 270.
infinity control of linear time delay systems [J ].
IEEE Trans on
[ 4 ] Molchanov A P , Pyatnitskiy Y S. Criteria of asymptotic stability of differential and difference inclusions encountered in control
theory [J ]. Systems & Control Letters , 1989 , 13 (1) : 59 - 64.
[ 5 ] Liberzon D , Morse S. Basic problems in stability and design of switching system [J ]. IEEE Control Systems , 1999 , 19 (10) : 59 -
70.
[ 6 ] Sun Y, Michel A N , Zhai G. Stability of discontinuous retarded functional differential equations with applications [J ]. IEEE Trans
on Automatic Control , 2005 , 50 (8) : 1090 - 1105.
[ 7 ] Yuan R , Jing Z , Chen L. Uniform asymptotic stability of hybrid dynamical systems with delay [J ].
IEEE Trans on Automatic
Control , 2003 , 48 (2) : 344 - 348.
[ 8 ] Ye H , Michel A N , Hou L. Stability theory for hybrid dynamical systems [J ]. IEEE Trans on Automatic Control , 1998 , 43 (4) :
461 - 474.
[ 9 ] Kim S , Campbell S A , Liu X. Stability of a class of linear switching systems with time delay [J ].
IEEE Trans on Circuits &
Systems I , 2006 , 53 (2) : 384 - 393.
[10 ] Dayawansa W , Martin C. Converse lyapunov theorem for a class of dynamical system with undergo switching [J ].
IEEE Trans on
Automatic Control , 1999 , 44 (4) : 751 - 760.
[11 ] Pyatnitskiy E S , Rapoport L B. Criteria of asymptotic stability of differential inclusions and periodic motions of time
varying
nonlinear control systems [J ]. IEEE Trans on Circuits & Systems Ⅰ, 1996 , 43 (3) : 219 - 229.
[12 ] Boyd S , Ghaoui E L , Feron E , et al. Linear Matrix Inequality in System and Control Theory [M]. Philadelphia : SIAM , 1994.
[13 ] Blanchini F. Nonquadratic Lyapunov functions for robust control [J ]. Automatica , 1995 , 31 (3) : 451 - 461.
[14 ] Cheng D , Guo L , Huang J . On quadratic Lyapunov function [J ]. IEEE Trans on Automatic Control , 2003 , 48 (5) : 885 - 890.
相关推荐
2023年江西萍乡中考道德与法治真题及答案.doc
2012年重庆南川中考生物真题及答案.doc
2013年江西师范大学地理学综合及文艺理论基础考研真题.doc
2020年四川甘孜小升初语文真题及答案I卷.doc
2020年注册岩土工程师专业基础考试真题及答案.doc
2023-2024学年福建省厦门市九年级上学期数学月考试题及答案.doc
2021-2022学年辽宁省沈阳市大东区九年级上学期语文期末试题及答案.doc
2022-2023学年北京东城区初三第一学期物理期末试卷及答案.doc
2018上半年江西教师资格初中地理学科知识与教学能力真题及答案.doc
2012年河北国家公务员申论考试真题及答案-省级.doc
2020-2021学年江苏省扬州市江都区邵樊片九年级上学期数学第一次质量检测试题及答案.doc
2022下半年黑龙江教师资格证中学综合素质真题及答案.doc
