大跨三塔悬索桥三维脉动风场模拟 .pdf-资料库

5 10 15 20 25 30 35 40 中国科技论文在线 http://www.paper.edu.cn 大跨三塔悬索桥三维脉动风场模拟# 邓稳平，王浩，邢晨曦** （东南大学土木工程学院，南京 210096）摘要：针对大跨三塔悬索桥的结构形式及振动形态的特点，结合自然风的相关特性，将实际的互相关三维脉动风速场简化为多个线状的不相关的一维脉动风速场。论述了利用谐波合成法对桥梁风场的模拟过程，其中考虑了风谱沿高度的变化和与频率有关的相位关系。基于谐波合成法和 MATLAB 平台，运用 FFT 技术编制了风场模拟程序，进行了某三塔悬索桥三维脉动风场的模拟，其中考虑了桥塔风效应的影响。应用随机信号分析处理技术对模拟样本进行校验，结果表明模拟值和目标值吻合良好，验证了该风谱模拟方法的有效性和可靠性。关键词：桥梁工程；三塔悬索桥；三维风场；数值模拟；谐波合成法中图分类号：U448.25 3-d turbulence wind field simulation for long-span triple-tower suspension bridge Deng Wenping, Wang Hao, Xing Chenxi (Civil Engineering school, Southeast University, NanJing 210096) Abstract: According to the structural styles and the vibration mode characteristics of long-span suspension bridges, and considering the correlation of natural wind, the correlation of the actual three-dimensional turbulence velocity field is simplified as a number of non-associated linear one-dimensional turbulence wind speed field. Discussed the bridge wind field simulation process by using spectral representation method, where takes into account the changes along the height of the wind spectrum and the phase relationship with the frequency. Combined with the spectral representation method and the fast Fourier trans form (FFT) technique, the digital simulation of 3-dimensional turbulence wind field for a triple-tower suspension bridge is carried out based on MATLAB, and the bridge tower wind effects are considered. The random signal analysis and processing technology is employed to verify the simulation sample. Results show that the digital simulation values can fit the object values well, which validate the efficiency and reliability of the presented wind field simulation method. Keywords: Bridge engineering; Triple-tower suspension bridge; 3-D wind field; Spectral representation method; Digital simulation 0 引言对于高耸结构、高层建筑结构、大跨度空间结构、大跨桥梁结构及高压输电塔线体系等，风荷载是结构设计时所必需考虑的一类重要的随机动力荷载[1]。桥梁结构在随机风荷载作用下的动力响应计算可分为频域法和时域法两大类[2]。频域法可以根据风荷载的统计特性和频谱信息直接获得结构响应的统计数据，操作比较方便，但该法只能对结构进行线性或线性化分析，有一定的局限性。对于大跨度桥梁结构，由于其高柔特性，由几何方面和气动弹性效应方面引起的非线性因素是不容忽视的。因此，为了进行较精确的非线性分析，只能采用时域法。要在时域内对大跨度桥梁进行风致振动分析，就要知道作用于结构上的风速时程，这就涉及到随机风场的模拟问题。风场的模拟主要是模拟脉动风场，一般归结为多维互相关零均值平稳高斯过程的数值模拟问题。用于模拟脉动风速时程的方法主要有线性滤波（ARMA）和谐波合成基金项目：国家自然科学基金项目(50908046)；国家教育部博士点基金资助项目(200802861012). 作者简介：邓稳平，（1988-），男，硕士研究生，从事桥梁抗风研究。通信联系人：王浩，（1980-）副研究员，主要从事桥梁健康监测与抗风研究。E-mail: wanghao1980@seu.edu.cn - 1 -

45 50 55 60 65 70 中国科技论文在线 http://www.paper.edu.cn （WAWS）两大系列。线性滤波系列计算速度快，但模拟参数难以确定。谐波合成系列理论完善，模拟精确，计算速度慢。谐波合成法是一种利用谱分解和三角级数叠加来模拟随机过程样本的传统方法，精度较高且无条件稳定。 1954 年，Rice[3]首先提出了谐波合成法的基本思想，当时只能模拟一维单变量的平稳高斯随机过程。Borgman[4]和 Shinozuka[5]解决了多维、多变量甚至非平稳随机过程的模拟问题。在此之后提出的方法得到了广泛应用，并在应用中不断得到改进。Yang[6]在计算中综合应用快速傅立叶变换(FFT)技术，大大提高了该类方法的计算效率。Yamazaki[7]提出了用于模拟非高斯随机过程的迭代谐波合成法方法。Deotatis[8]应用 FFT 技术结合双索频率的概念模拟了各态历经的多变量平稳随机过程--沿不同高度分布的多点脉动风速，模拟了各态历经的多变量平稳高斯随机过程中。李永乐[9]、韩大建[10]、白海峰[11]、王浩[12]等将三维脉动风场简化为多个一维脉动风速场。曹映泓[13]应用特殊情况下谱矩阵的显式分解，大大提高了该方法的计算效率，成功模拟了大跨度桥梁沿主梁的脉动风速。丁泉顺[14]等通过对谱分解矩阵引入插值近似，减少谱分解的次数，从而提高该谐波合成法的计算效率。罗俊杰[15]采用 3 次均匀 B 样条插值方法来拟合分解谱密度函数曲线，然后用递归优化算法进行矩阵的 Cholesky 分解，加快了脉动风场合成的速度。李黎[16]、李杰[1]、李元齐[17]等将特征正交分解的强形式，即基于功率谱矩阵的随机过程特征正交分解(SPT)引入到谱表示法中，代替原有的对功率谱矩阵的 Cholesky 分解，极大地提高了计算效率。本文将实际的互相关三维脉动风速场简化为多个线状的不相关的一维脉动风速场。基于谐波合成法，并运用 FFT 技术编制 MATLAB 风场模拟程序，进行了某三塔悬索桥主梁脉动风场的模拟；并考虑了风谱沿高度的变化以及与频率有关的相位关系，对主塔的随机脉动风速进行了模拟。应用随机信号分析处理技术对模拟样本进行校验，结果表明模拟值和目标值吻合良好，验证了该风谱模拟方法的有效性和可靠性。 1 风场特性的基本特性风是大气边界层内空气流动的现象，并且其流动的速度和方向具有随时间和空间随机变化的特征。桥梁结构物主要受所在地近地风的影响，即大气边界层内空气流动特性的影响。结构物所在地的近地风特性是进行结构物抗风设计与检算的基本依据。为研究方便，我们本质上是随机的自然风，分解成以平均和均值为零的脉动风分别加以研究。 1.1 大跨度悬索桥随机风场简化在笛卡尔坐标系下，大跨度桥梁三维风场可以表示为[12]： + , U U z u x y z t = ( ) ( , , ) x y z t ( , , ) υ υ = x y z t ( , , ) ω ω = , , (1) 75 式（1）中，x 轴为横桥向，即风的主流方向；y 轴为顺桥向，与风的主流方向垂直；z 轴为竖向，亦与风的主流方向垂直；t 表示时间。u，v，ω 分别表示横桥向，顺桥向和竖向的脉动风速； ( )U z 为主流方向的平均风速，用指数分布律表示为： U U z 2 z 1 ⎛ = ⎜ ⎝ z 2 z 1 α ⎞ ⎟ ⎠ (2) 式（2）中，Uz1，Uz2 分别为高度 z1、z2 的风速；α 为考虑地表粗糙度影响的无量纲幂 - 2 -

中国科技论文在线指数，A 类场地取 0.12。 http://www.paper.edu.cn 80 由于自然风在 x，y，z 三个方向上的脉动分量间的相关性较弱，且目前对三个脉动分量之间的相关关系缺乏卓有成效的研究，实际应用中通常不考虑风速在 x，y，z 三个方向之间的相关性，而仅考虑风速在空间上的相关性，从而在理论上将三维相关的风速场简化为三个方向上独立的一维风速场，亦即将三维相关的多变量随机过程简化为三个独立的一维多变量随机过程。由于主缆的重力刚度很大，并且其受风面积相对于主梁和主塔要小得多，故对大跨度悬索桥总体风致响应分析中，可以仅考虑桥塔和主梁的脉动风场。 85 90 95 100 105 110 对于桥塔为竖向线状结构，可以忽略竖向脉动风分量 w 对其作用，由于主塔的顺桥向受到主缆和边缆的强制约束，强风作用下其顺桥向振动主要受主缆和主梁竖弯振动的影响，顺桥向脉动风分量 v 对其振动的影响很小，故可以忽略上述两个脉动分量的影响，从而桥塔上只考虑横桥向的脉动风分量 u。对于大跨度悬索桥的主梁而言，由于在顺桥向为线状结构，故可忽略顺桥向的脉动风分量 v 的作用，从而只考虑横桥向和竖向脉动风分量 u 和 w。当大跨度悬索桥采用双塔或多塔结构时，由于桥塔间距较大，可忽略各桥塔之间风速的相关性。桥塔与主梁跨中附近各点距离较大，因此横桥向脉动风场的相关性同样可以忽略；塔梁结合处附近各点风速的相关性较强，但由于该处结构所受约束较强，所以风致振动通常较小，风对其的广义作用力仍然较小。因此，在横桥向脉动风场模拟时，可以忽略桥塔和主梁之间风速的相关性，分别将其作为独立的随机风场来考虑。 1.2 脉动风功率谱密度函数功率谱密度函数是平稳随机过程的主要数字特征，脉动风速的功率谱函数体现了紊流中各频率成分所作贡献的大小。许多风工程专家对风速功率谱进行了研究，得到了不同形式的风谱表达式[17]。其中用于结构设计的水平脉动风速谱主要有 Davenport 谱、Kaimal 谱和 Harris 谱等；竖向脉动风速谱 Panofsky-McCormick 谱、Lumley-Panofsky 谱等。后来经人多次改进，目前《公路桥梁抗风设计规范》建议的功率谱表达式是采用 1972 年 Kaimal 提出的表达式，现介绍如下。高度 Z 处平均风速 U（z）的顺风向脉动风功率密度函数为： unS n ( ) u ( ) * 2 = f f (1 50 ) 200 + 5/3 (3) 竖向脉动风速功率谱函数为： nS n ( ) ω u ( ) * 2 = f 6 + f (1 4 ) (4) 2 式中： Su（n）——顺风向功率谱密度函数 Sω（n）——竖风向功率谱密度函数 n——风的脉动频率 f = nZ U z ( ) ——莫宁坐标 u*——气流摩阻速度 - 3 -

中国科技论文在线 1.3 脉动相关性 http://www.paper.edu.cn 115 脉动风在不同时间和空间上的相关性是风工程研究的一个重要参数，其相关程度在频域中用相干函数来描述[18]。对于迎风面尺度较大的结构必须考虑脉动风的空间相关性，风洞试验和实测表明，相干函数是一条指数衰减曲线。对于侧向和竖向尺寸较大的结构， Davenport 建议的空间相干函数为 Coh j m , ( ) ω = exp ⎧ ⎪ −⎨ ⎪ ⎩ ω ∑ r U z ( ( π C r ( 2 r j − r m 2 ) ) + U z ( )) m j (5) ⎫ ⎪ ⎬ ⎪ ⎭ 式中，r=y，z；rj，rm 表示 j，m 两点的空间坐标。U（Zi），U（Zm）为 j，m 两点的平 120 均风速；Cy，Cz 分别表示横向和竖向的相关指数衰减系数，Emil 建议 Cy=16，Cz=10。在生成桥面的风速样本序列时，近似假定桥面处于同一高度，风场沿桥跨方向是均匀的。这种情况下，Simiu 假定关于桥面任意两点处风速作用是同相位的。与之相呼应，目标谱密度阵为实数对称阵形式。 125 而当需要考虑桥塔上的风速时程影响时，由于风速作用于不同的高度，实际上并不是同相位的，即阵风会先作用于结构较高处，时间差 τ 之后，才作用于较低处。要有效地模拟风，就应考虑风的这些特性，不同高度处互谱密度函数的相位角 φ（n）的经验公式如下： ( ϕ n ∗ ) ⎧ ⎪= − ⎨ ⎪ ⎩ n / 4 ∗ π n 10 ∗ + π random 1.25 n ∗ ≤ 0.1 0.125 0.1 < n ∗ ∗ n > ≤ 0.125 (6) 式中 n * = n z ( j ) + j U z (( ( z − m U z ( ) m )) 2 ，random 为[-π，π]上的均匀随机数。 2 一维多变量随机过程的模拟 130 2.1 谐波合成法考虑一个一维、n 变量、零均值的高斯随机过程{f（t）}。它包含 f1（t），f2（t）…fn （t）共 n 个随机变量。其互谱密度矩阵为： ⋅⋅⋅ ⋅⋅⋅ ⋅⋅⋅ ⋅⋅⋅ S ( ) 0 ω 12 S ( ) 0 ω 22 ⋅⋅⋅ S ( ) 0 ω n 2 S ( ) 0 ω 11 S ( ) 0 ω 21 ⋅⋅⋅ S ( ) 0 ω n 1 ( ) ω ⎡ ⎢ ⎢ ⎢ ⎢ ⎢ ⎣ = S 0 S ( ) 0 ω n 1 S ( ) 0 ω n 2 ⋅⋅⋅ S ( ) 0 ω nn ⎤ ⎥ ⎥ ⎥ ⎥ ⎥ ⎦ (7) 根据 George Deodatis 理论[6]，随机过程{f（t）}的样本可以由下式来模拟： 135 f j t ( ) = 2 j N ∑∑ m 1 = l H jm ( ω ω ω θ ω ml cos( Δ − jm ml ml ( ) t ) )mlφ+ ， j=1，2，…n (8) 式中各变量意义如下： - 4 -

中国科技论文在线 http://www.paper.edu.cn N 为一充分大的正整数， ωΔ = ，为频率增量，ωu 为截断圆频率，即当 ω>ωu 时， ω u N S0（ω）＝0，这样，无论从数值计算角度还是从物理意义上，大于 ωu 的频率成分都不会再造成影响。φml 为均匀分布在（0，2π）区间的随机相位角数列。 140 Hjm（ωml）是 H(ω)矩阵中的元素。H（ω）为 S0（ω）的 Cholesky 分解，即： H ( ) ω = 0 S H ⎡ ⎢ H ⎢ ⎢ ⎢ ⎣ H 11 * T ) ( H H ( ) ) = ω ω ω ( ) ω ( ) ω 21 ⋅⋅⋅ ( ) ω 0 ( ) ω 22 ⋅⋅⋅ ( ) ω ( ⋅⋅⋅ ⋅⋅⋅ ⋅⋅⋅ ⋅⋅⋅ H H n 2 n 1 (9) 0 0 ⋅⋅⋅ ( ) ω nn ⎤ ⎥ ⎥ ⎥ ⎥ ⎦ H (10) 由于 S0（ω）通常情况下为一复数矩阵，且不一定正定，因此 H（ω）通常也是复矩阵，其对角元素为实数，非对角元素为复数。HT*（ω）为其共轭转置矩阵。H（ω）中的元素之间有如下关系成立： 145 H H jm ( ) ω = ( ) = Hω ( ) − ，j=1，2，…n (11) ω jj jj jmi ( ) e θ ω H ，j=1，2，…，n， m=1，2，…，j-1，j>m (12) ) ω − * jm ( 150 θjm（ω）为 Hjm（ω）的复角，由下式给出： ( ) ω ) ( ω ⎧ ⎪ ⎨ ⎪ ⎩ Im 和 Re 分别表示取虚部和实部。为了增大模拟样本的周期，ωml 可按如下取值： ) θ ω Im Re H H tan ⎤ ⎦ ⎤ ⎦ ⎡ ⎣ ⎡ ⎣ = 1 − jm jm jm ( ⎫ ⎪ ⎬ ⎪ ⎭ (13) ω ml = − Δ + ω ω Δ ，l=1，2，…， N (14) l ( 1) m n 155 可以证明，当 N→∞时，式（8）模拟的随机过程满足式（7）的目标谱为了避免式（8）的模拟结果失真，t 的增量 tΔ 须满足以下条件： (15) 2 t π Δ ≤ 2 u ω 式（8）模拟的随机过程的周期为： n nN 2 2 T π π Δ ω ω u = = 0 (16) 由以上可知，只要已知 S0（ω），恰当地选择 N，ωu，Δt，就可以获得好的随机过程的 160 样本。 2.2 主梁风场的模拟在实际工程中，空间不同点之间的密度通常用实数函数来表示[13]，因此式（7）可以简化为实数矩阵。当模拟桥主梁上若干点的水平风速时，将水平风速看作一个一维多向量的高斯随机过程，并近似认为水平风谱沿水平方向是不变的，即主梁上各点的水平风谱是相同的，有下式成立： 165 - 5 -

中国科技论文在线 = S ( ) ω = ⋅⋅⋅ = S ( ) ω S 0 11 ( ) ω 0 22 S 0 jm ( ) 0 ω ω jj Coh ω 为相干函数。 S ) 0 mm = S ) ( , ( j i 式中 ( ) ω 0 nn Coh i http://www.paper.edu.cn = 0 S ( ) ω (17) ( ) ω = 0 S Coh ( ) ω i , j ( ) ω , j (18) 考虑桥面上等距分布的 n 个点，间距为Δ ，则有 jm Δ = Δ − 。采用 Davenport 提出 j m 170 的相干函数，即： Coh j ，m ( ) ω = exp( − C Δ ω z jm U z ( ) 2 π ) = exp( − C j m Δ − ω z U z ( ) 2 π ) = (exp( − zC Δ ω U z ( ) 2 π j m − )) = C j m − 式中 CZ=10 为脉动风横向衰减因子，U（z）为桥面处的平均风速，C 是 ω 的函数。 C = exp( − zC Δ ω U z ( ) 2 π ) (20) (19) 175 将式（17）~（20）代入式（7）中可得： 0 S ( ) ω ω = S ) ( 1 C C 2 ⋅⋅⋅ C n ( 1) − ⎡ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎣ 1 C ⋅⋅⋅ n ( − 1 ⋅⋅⋅ n ( − 3) 2) C Sym ⋅⋅⋅ ⋅⋅⋅ ⎤ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎦ 1 (21) C 将式（21）进行 Cholesky 分解。由于0 < ，故 ( 1C< )H ω 为实矩阵，因此有 ∗ T H Hω ( ) (22) 0 jmθ = (23) 运用 FFT 技术可以大大地减少风场模拟的计算量，进一步提高计算效率。为此，我们 ( ) ω = T 可以将式（8）改写为如下形式： 180 185 j m ( ( h q t Δ Δ = ) Re{ f p t j p tω Δ )( Δ 3 N n 2 × − 其中，q 是 / 2p N 的余数， 1, 2, − n 1 0,1,2 q = ∑ 1 = p i ) exp[ ( j 1, = jmh = jm m ; h jm ( q t Δ = ) 2 N 1 − ∑ l = 0 B l ( jm ω Δ )exp( i 其中， B l ( jm ) ω Δ 2 ⎧ ⎪ = ⎨ ⎪⎩ Δ + ω ω H l ( jm m 0 ω Δ n )exp( i φ ml ) )]} (24) 1, 2, n ) ( q tΔ 由下式给出： lq π N ) l N 0 ≤ ≤ N l 2 ≤ ≤ N (26) (25) 由式（25-26）可知，hjm（qΔt）即是 Bjm（lΔω）的 Fourier 逆变换，因此可以用 FFT 来 190 计算。 - 6 -

中国科技论文在线 2.3 主塔风场的模拟 http://www.paper.edu.cn 模拟桥塔的风速时程时，由于桥塔上各点的风速不同，互谱密度函数需要考虑相位角，风谱密度矩阵（复数矩阵）有可能不正定。一般情况下脉动风的互谱密度函数为： S S = ( ) 0 ω jm jjS ω ， 0 ( mmS ω 为不同高度两点 j，m 的自谱密度函数， )nϕ ∗ 是考虑的相位差。 i n ( ( ω ϕ ∗ ( ) ω ω 式中， 0 ( )exp( Coh 0 mm )) S 0 jj ) ( ) ( jm ) (27) jmCoh ω 为相关函数。 ( ) 在考虑相位角后，谱密度矩阵可能不正定。对应风谱密度矩阵的正定性与否将风频值划分为正定区间和不正定区间。在风频值正定区间内，可直接将风谱密度矩阵进行 Cholesky 分解；而在风频值不正定区间内，采用插值技术近似获得风谱密度矩阵分解式[19]。分解步骤如下：（1）依据给定条件得出风频值的不正定区间（f1，f2），记 f1，f2 对应的 H1、H2 的幅角矩阵分别为 θ1、θ2；（2）当风频值 f 在（f1，f2）内时，先不考虑不同点处的相位角，将 S(f)按实对称矩阵进行 Cholesky 分解得到 H ，然后在 θ1、θ2 之间线性插值得到幅角矩阵θ，则此时 H（f）可近似表示为： jkH = H exp( iθ jk ) jk (28) 其中， 195 200 205 (29) （3）当风频值 f 在正定区间内时，直接进行 Cholesky 分解得到 H（f）。同样 Cholesky θ θ 1, )( θ θ 1, ) / ( − − − = + ( ) 2, jk jk jk jk f 1 f 1 f 2 f 210 分解之后运用 FFT 技术得到主塔风速时程，不再赘述。 3 考虑桥塔风效应的三塔悬索桥风场模拟实例针对一座跨度为 2×1080 米的三塔两跨悬索桥，其风场可以简化 5 个独立的一维多变量随机风场。如表 1 所示。运用本文上述方法，作者模拟了桥面上沿跨度方向等间距分布 80m 主梁 215 风场、沿竖向等间距分布 30m 的主塔风场。模拟点分布如图 1 所示。表 1 简化的 5 个独立的一维脉动风场 Table 1 Five independent simplified one-dimensional turbulence wind field 风场号 1 2 3 4 5 位置主梁主梁左边塔中塔右边塔方向横桥向竖向横桥向横桥向横桥向间距 80m 80m 30m 30m 30m 模拟点数 28 28 7 7 7 220 Fig.1 Simulated point layout for three-dimensional turbulence wind field (unit: m) 图 1 三维脉动风场模拟点布置(单位: m) 模拟计算的主要参数如下： - 7 -

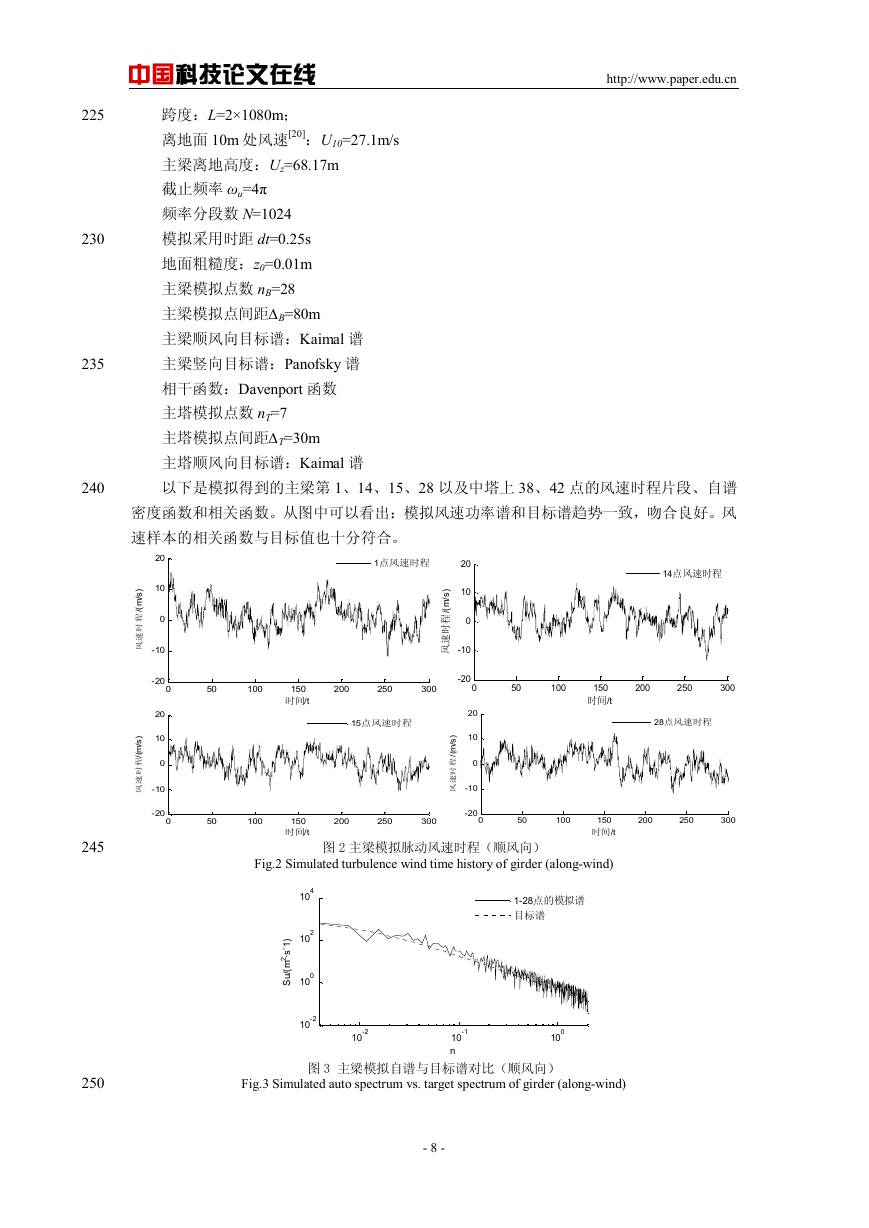
225 230 235 240 245 250 中国科技论文在线 http://www.paper.edu.cn 跨度：L=2×1080m；离地面 10m 处风速[20]：U10=27.1m/s 主梁离地高度：Uz=68.17m 截止频率 ωu=4π 频率分段数 N=1024 模拟采用时距 dt=0.25s 地面粗糙度：z0=0.01m 主梁模拟点数 nB=28 主梁模拟点间距∆B=80m 主梁顺风向目标谱：Kaimal 谱主梁竖向目标谱：Panofsky 谱相干函数：Davenport 函数主塔模拟点数 nT=7 主塔模拟点间距∆T=30m 主塔顺风向目标谱：Kaimal 谱以下是模拟得到的主梁第 1、14、15、28 以及中塔上 38、42 点的风速时程片段、自谱密度函数和相关函数。从图中可以看出：模拟风速功率谱和目标谱趋势一致，吻合良好。风速样本的相关函数与目标值也十分符合。 ) s / m ( / 程时速风 ) s / m ( / 程时速风 20 10 0 -10 -20 0 20 10 0 -10 -20 0 1点风速时程 50 100 150 时间/t 200 250 300 15点风速时程 50 100 150 时间/t 200 250 300 ) s / m ( / 程时速风 20 10 0 -10 -20 0 ) s / m ( / 程时速风 20 10 0 -10 -20 0 14点风速时程 50 100 150 时间/t 200 250 28点风速时程 300 图 2 主梁模拟脉动风速时程（顺风向） Fig.2 Simulated turbulence wind time history of girder (along-wind) 50 100 150 时间/t 200 250 300 104 102 100 10-2 ) 1 - s · 2 m ( / u S 1-28点的模拟谱目标谱 10-2 10-1 n 100 图 3 主梁模拟自谱与目标谱对比（顺风向） Fig.3 Simulated auto spectrum vs. target spectrum of girder (along-wind) - 8 -

资料库

大跨三塔悬索桥三维脉动风场模拟 .pdf

相关推荐

开发技术

热门标签

最新资料