logo资料库

2018年国赛优秀论文A题.pdf

发布时间：2022-06-29 发布人：admin 分类：说明书 资料大小：0.97M 资料格式：pdf 举报 版权申诉
第1页 / 共31页
第2页 / 共31页
第3页 / 共31页
第4页 / 共31页
第5页 / 共31页
第6页 / 共31页
第7页 / 共31页
第8页 / 共31页
资料共31页，剩余部分请下载后查看
    高温作业服设计 【摘要】 高温作业服可以避免高温灼伤，在实际作业中有广泛应用。本文对高温作业服的优 化设计进行研究，分析作业服的传热过程，综合考虑各种传热方式、边界和初始条件， 建立非稳态一维传热模型，并应用于作业服厚度的优化设计。 对于问题一：通过分析传热模型特点，将三维问题简化为一维问题，研究非稳态传 热过程。主要考虑热传导、热对流两种传热方式，建立基于能量守恒定律的偏微分控制 方程组，确定初边值条件，得到作业服非稳态一维传热过程的数学刻画。基于最小二乘 原理，建立最优化模型，拟合实测温度求解未知参数的最优估计。利用有限差分法逐层 求解方程组，并搜索得到第一层和第四层换热系数的参数估计分别为：113W/(m2·k)和 8.344W/(m2·k)。再利用参数估计值计算出温度分布，生成 Excel 文件。扩展模型并检 验忽略热辐射的合理性，考虑辐射传热，两端换热系数为：113W/(m2·k)和 8.496 W/(m2·k)。表明热辐射对传热过程影响较小可以忽略。 对于问题二：以第二层厚度最小为优化目标，综合 60min 内最大温度、超过 44℃ 时间和厚度范围等约束，建立厚度调整单变量优化模型。将模型求解转换为约束条件临 界值求解问题，得到第二层和第四层最小厚度分别为：17.5mm，此时最大温度为 44.0799℃，超过 44℃时间低于 5min。从理论和结果进行分析，得到第二层材料对最大 温度影响占次要因素，厚度增加主要影响传热速度的结论。 对于问题三：考虑舒适性、节约性、性能稳定性和研发效率等因素，以第二层和第 四层厚度最小为优化目标，综合 30min 内最大温度、超过 44℃时间和厚度限制等约束 条件，建立作业服设计的多目标优化模型。求解过程中，将多目标问题转化为单目标问 题，根据问题二解法求解得到第二层和第四层最优厚度设计分别为：19.2mm 和 6.4mm。 此时最大温度为 44.7721℃，超过 44℃时间低于 5min。扩展模型，研究各层材料在传热 过程中的不同作用效果，得到：第二层材料可延缓传热过程，适用于长时间作业环境； 第四层材料增强隔热性能，适用于高温作业环境的结论。 最后对本文所建立模型进行了讨论和分析，综合评价模型，并提出了改进和推广的 方向。 关键词： 非稳态一维传热过程 有限差分法 优化模型 1
    1.1 问题背景 1 问题重述 高温作业服可避免人们在高温环境下作业受到灼伤。而高温作业服的设计除要考虑 避免灼伤外，还需要尽量降低研发成本、缩短研发周期。设计过程中，在高温环境放置 假人，并测量皮肤外侧温度。为实现设计目的，需要根据假人皮肤外侧温度信息，建立 高温工作服的非稳态传热模型，并应用模型求解温度分布和作业服设计。该问题具有以 下特征和要求： (1)防护服分为 4 层，其中Ⅰ、Ⅱ、Ⅲ层为织物制造，第Ⅳ层为织物与皮肤之间的空 气间隙；第Ⅰ层直接与外部环境接触。 (2)假人体内恒温为 37℃。 (3)应建立非稳态传热模型，反应不同时间节点的传热情况。 (4)设计目的要避免灼伤并考虑研发成本和周期。 1.2 求解问题 本文根据问题建立数学模型，并设计求解方法解决如下问题： 问题一： 根据附件一中服装材料参数及各层厚度，综合考虑各种传热方式，建立作业服非稳 态传热模型。根据附件二中实测温度值，估计传热模型中相关参数值，并计算温度分布。 问题二： 不同于问题一，问题二中环境温度改变为 65℃，第四层厚度为 5.5mm。以工作 60min，最大温度不超过 47℃，超过 44℃时间低于 5 分钟作为约束条件，建立以第二层 材料厚度最小为目标的优化模型，应用非稳态传热模型求解最优设计，并分析结果及原 因。 问题三： 问题三需同时考虑第二层和第四层厚度设计，约束条件为最大温度 47℃和高温时 间低于 5 分钟。需要通过建立模型求解第二层和第四层厚度的最优化设计问题。 2
    2 问题分析 高温作业服的设计问题，实质上是综合考虑各种传热方式，对作业服建立非稳态传 热模型，并应用于求解温度分布和参数优化问题。模型的核心在于传热模型的建立及应 用。 2.1 问题一分析 问题一已给定各层材料厚度及环境温度。并测试得到了假人皮肤外侧的温度变化信 息。要求解温度分布，需要根据题目信息，综合考虑各种传热方式及边界条件，建立完 整的传热模型。对于模型建立过程中的未知参数，通过传热模型建立参数与实测温度的 数值关系描述，并求解得到最优参数应用于后续求解过程。 作业服传热模型考虑的是非稳态传热，即需要建立温度与时间的关系，得到整个传 热过程的具体时间描述，刻画非稳态过程的温度分布及传热特性。 2.2 问题二分析 问题二实质上是建立在问题一非稳态传热模型基础上的参数优化模型。目的是求解 第二层的最优厚度。此处最优应使制造成本尽量小，以厚度最小化作为优化目标，以皮 肤外侧温度和超过 44℃的时间作为约束条件，求解满足条件的作业服最优设计。 2.3 问题三分析 问题三额外增加了第四层的厚度设计，需综合考虑研发制作成本、衣服笨重程度、 人体舒适程度等因素，建立多目标优化模型。在满足最大温度约束和高温时间约束的条 件下，通过非稳态传热模型求解最优设计。为进一步深入研究作业服的传热过程和实际 应用，对模型进一步扩展进行研究。 3
    3 模型假设 假设 1：不考虑作业服水汽、汗液蒸发等传热传质过程； 假设 2：以第四层(空气层)底层温度表示人体皮肤外侧温度； 假设 3：不考虑接触面之间的接触热阻，认为接触面界面连续； 假设 4：简化为一维传热问题，不考虑其他不均匀热源和传热过程； 假设 5：人体为绝对黑体，即辐射发射率为 1。 表 1：符号说明 变量 λj, (j=1,2,3,4) ρj, (j=1,2,3,4) Cj, (j=1,2,3,4) h1 h2 q T Tren Ten E 4 符号说明 说明 导热系数 材料密度 比热容 第一层与外界对流换热系数 第四层与人体对流换热系数 热流密度 温度 人体温度(37℃) 环境温度 辐射力(辐射能量密度) dj, (j=1,2,3,4) ε q 辐射 材料厚度 发射率 辐射传热量 5 模型准备 量纲 W/(m·℃) kg/m3 J/(kg·℃) W/(m2·℃) W/(m2·℃) W/m2 ℃ ℃ ℃ W/m2 mm - W/m2 5.1 背景知识 5.1.1 传热方式 4
    热力学过程有三种基本传热方式： (1)热传导：微观粒子热运动而产生的热能传递，固、液、气内部传热均存在热传 导，主要基于傅里叶定律计算； (2)热对流：由流体宏观运动引起的热量传递过程，主要考虑流体与物体接触面的 热交换，基于牛顿冷却公式计算； (3)热辐射：物体通过电磁波传递能量，可发生在任何物体中。 5.1.2 边界条件 导热问题常见边界条件有三类，令 T(x,y,z,t)为物体的温度分布函数，Γ 为物体的 边界曲面。 (1)第一类边界条件：规定边界上的温度值； (1) (2)第二类边界条件：规定边界上的热流密度； (2) (3)第三类边界条件：规定边界上物体与周围流体间的对流传热系数及周围流体温 度。 5.1.3 稳态/非稳态 (3) 稳态传热过程指各点温度不随时间变化，控制方程中无时间项；非稳态传热即求解 瞬态问题，各点温度随时间变化，控制方程中有时间项。 5.1.4 傅里叶传热定律 傅里叶定律是热传导基本定律，描述温度差与热流密度的关系。 (4) 式中：q 为热流密度，λ 表示传热系数，dt/dx 表示空间节点上的温度差。对于考虑 热传导的部分，主要基于傅里叶定律建立模型。 5.1.5 牛顿冷却公式 5 (,,)(,,,)(,,,)xyzTxyztfxyzt=(,,)(,,,)xyzTfxyztn=(,,)()(,,,)xyzTTfxyztn+=dTqdx=−
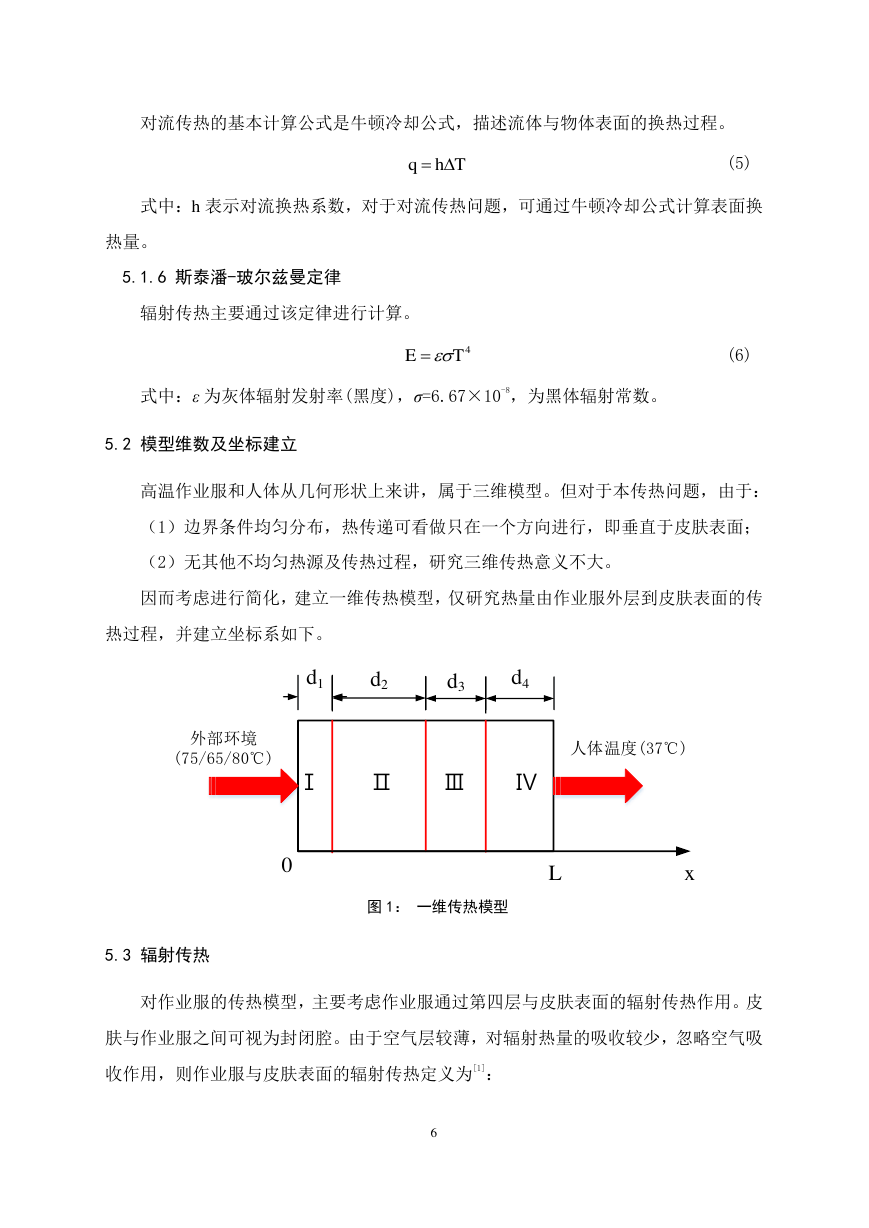
    对流传热的基本计算公式是牛顿冷却公式，描述流体与物体表面的换热过程。 (5) 式中：h 表示对流换热系数，对于对流传热问题，可通过牛顿冷却公式计算表面换 热量。 5.1.6 斯泰潘-玻尔兹曼定律 辐射传热主要通过该定律进行计算。 (6) 式中：ε 为灰体辐射发射率(黑度)，σ=6.67×10-8，为黑体辐射常数。 5.2 模型维数及坐标建立 高温作业服和人体从几何形状上来讲，属于三维模型。但对于本传热问题，由于： （1）边界条件均匀分布，热传递可看做只在一个方向进行，即垂直于皮肤表面； （2）无其他不均匀热源及传热过程，研究三维传热意义不大。 因而考虑进行简化，建立一维传热模型，仅研究热量由作业服外层到皮肤表面的传 热过程，并建立坐标系如下。 图 1： 一维传热模型 5.3 辐射传热 对作业服的传热模型，主要考虑作业服通过第四层与皮肤表面的辐射传热作用。皮 肤与作业服之间可视为封闭腔。由于空气层较薄，对辐射热量的吸收较少，忽略空气吸 收作用，则作业服与皮肤表面的辐射传热定义为[1]： 6 qhT=4ET=ⅠⅡⅢⅣ外部环境(75/65/80 )人体温度(37 )x0Ld1d2d3d4
    (7) 式中：εg 和 εskin 分别表示作业服与皮肤表面的发射率，Tg 和 Tskin 分别为第三层右边 界温度和皮肤外侧温度。由于作业服辐射发射率较低。此处认为：非稳态传热模型中辐 射传热作用很小，可以忽略，并在后续部分验证此假设合理性。 5.4 各层传热方式 对于传热问题，往往需要综合考虑热传导、热对流和热辐射三种不同传热方式。不 同的传热方式有其特点和适用的情况。因而对各层材料和各边界条件进行讨论，确定需 要各自的传热方式。 (1)第Ⅰ层材料 对于第一层材料，材料内部主要为热传导方式，根据傅里叶定律建立模型；材料外 边界与外部环境接触的边界条件为第三类边界条件，为对流传热过程。 (2)第Ⅱ层材料 第二层材料仅需考虑热传导的传热方式。 (3)第Ⅲ层材料 第三层材料内部为热传导方式；由于第四层空气层较薄，故接触面不考虑对流传热， 仅考虑热传导[2]。 (4)第Ⅳ层材料 第四层材料内部仅考虑热传导；材料右边界与人体接触，人体皮肤下存在大量毛细 血管的血液流动，故右边界为第三类边界条件，考虑对流传热。 6.1 问题分析 6 问题一：非稳态传热模型 问题一已给定各层厚度，并已有皮肤外侧温度分布测量值。根据上述模型准备部分， 基于能量守恒定律，可建立非稳态偏微分传热控制方程，确定初值和边界条件。进而建 7 44[]111gskingskinTTq−=+−辐射
    立作业服非稳态传热模型。模型中两个对流传热系数未知，通过传热模型建立系数与实 测温度之间的数值关系描述，搜索求解拟合最优化问题，得到最优传热系数，应用于后 续作业服厚度设计。 6.2 模型建立-非稳态传热模型 6.2.1 传热控制方程 对于非稳态传热问题，依据能量守恒定律建立非稳态偏微分控制方程，即：对任一 微元体，其热力学能的变化(表现为温度变化)等于流入流出微元体热流量的差值[3]。控 制方程为： (8) 式中：左项表示微元体热力学能变化；右项表示微元体流入流出热流量差值。 6.2.2 边界条件及初值条件 对于整个作业服传热模型，两端均为第三类边界条件，传出热量由对流换热带走。 假设进入高温环境时人体与作业服已达到稳定状态，作业服温度分布的初始值为假人温 度 37℃。 (9) 式中：h1 和 h2 分别表示两端的对流传热系数，T(0,t)和 T(L,t)分别表示两端界面温度， T(x,0)为初始条件，Ten 表示环境温度，Tren 表示人体温度。 6.2.3 材料接触面 对于不均匀材料导热问题，已假设材料间接触良好，忽略接触热阻，满足界面连续 条件，即满足界面上温度与热流密度连续的条件： (10) 式中：i 表示各个接触面。 8 ()(1,2,3,4)jjjTTcjtxx==11042((0,))((,))(,0)enxrenxLrenThTTtxThTLtTxTxT==−=−−=−=1(,)(,)(1,2,3)(,)(,)iiiiiiTxtTxtiTTxtxtxx−+−++===
    分享到：
    赞 收藏

    相关推荐

    资料库

    存储

    共收录294份资料，累计8个分类，关注成员有19位，主要包括：EMC,SUN,IBM,Dell,HP,Microsoft,Veritas,其它

    热门标签

    EMC SUN IBM Dell HP Microsoft Veritas 其它

    最新资料