2015年浙江省中国计量大学自动控制原理考研真题.doc

发布时间：2022-09-19 发布人：admin 分类：说明书资料大小：0.19M 资料格式：doc 举报版权申诉

第1页 / 共5页

2015年浙江省中国计量大学自动控制原理考研真题.doc.pdf-第2页.jpg

第2页 / 共5页

2015年浙江省中国计量大学自动控制原理考研真题.doc.pdf-第3页.jpg

第3页 / 共5页

2015年浙江省中国计量大学自动控制原理考研真题.doc.pdf-第4页.jpg

第4页 / 共5页

2015年浙江省中国计量大学自动控制原理考研真题.doc.pdf-第5页.jpg

第5页 / 共5页

文本预览

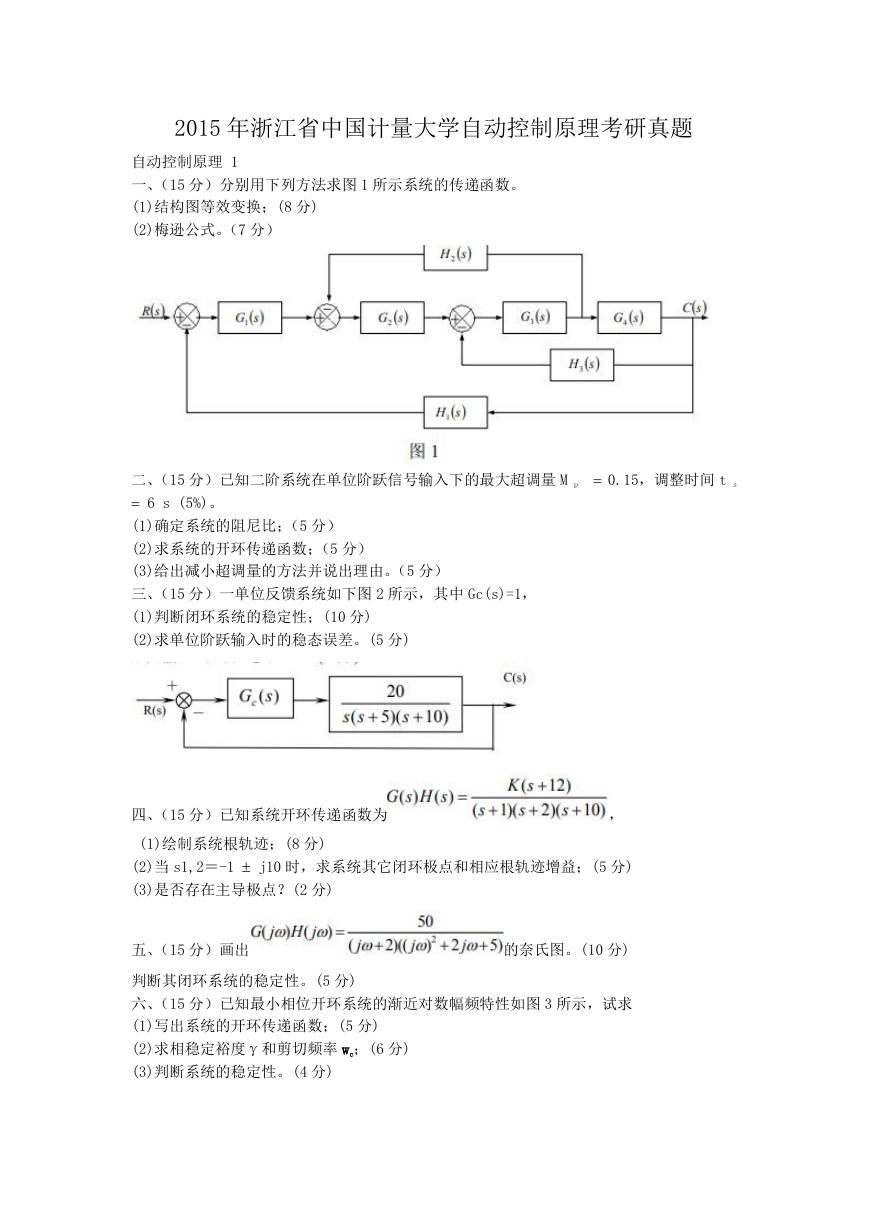
2015 年浙江省中国计量大学自动控制原理考研真题自动控制原理 1 一、（15 分）分别用下列方法求图 1 所示系统的传递函数。 (1)结构图等效变换；(8 分) (2)梅逊公式。（7 分）二、（15 分）已知二阶系统在单位阶跃信号输入下的最大超调量 M p  0.15，调整时间 t s  6 s (5%)。 (1)确定系统的阻尼比；（5 分） (2)求系统的开环传递函数；（5 分） (3)给出减小超调量的方法并说出理由。（5 分）三、（15 分）一单位反馈系统如下图 2 所示，其中 Gc(s)=1， (1)判断闭环系统的稳定性；(10 分) (2)求单位阶跃输入时的稳态误差。(5 分) 四、（15 分）已知系统开环传递函数为， (1)绘制系统根轨迹；(8 分) (2)当 s1,2＝-1  j10 时，求系统其它闭环极点和相应根轨迹增益；(5 分) (3)是否存在主导极点？(2 分) 五、（15 分）画出的奈氏图。(10 分) 判断其闭环系统的稳定性。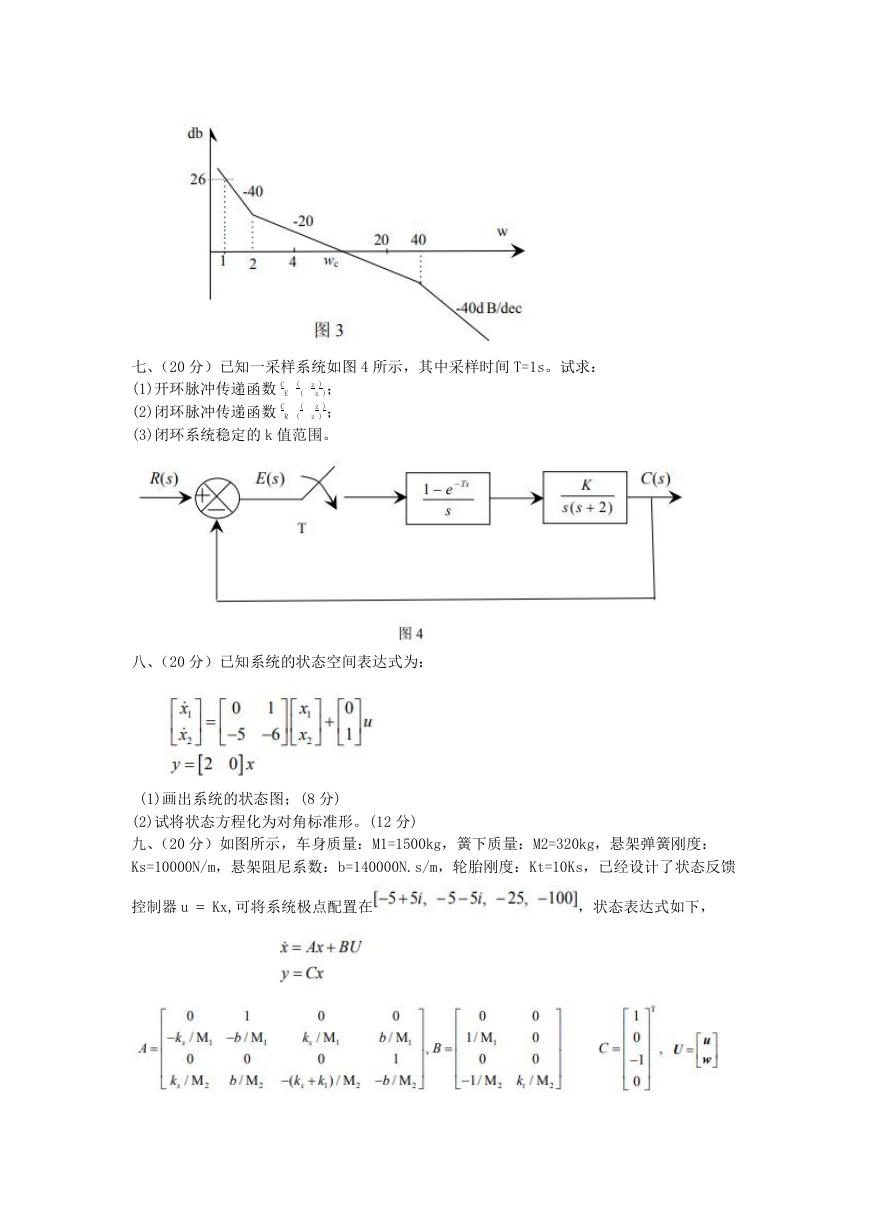(5 分) 六、（15 分）已知最小相位开环系统的渐近对数幅频特性如图 3 所示，试求 (1)写出系统的开环传递函数；(5 分) (2)求相稳定裕度γ和剪切频率 wc；(6 分) (3)判断系统的稳定性。(4 分)

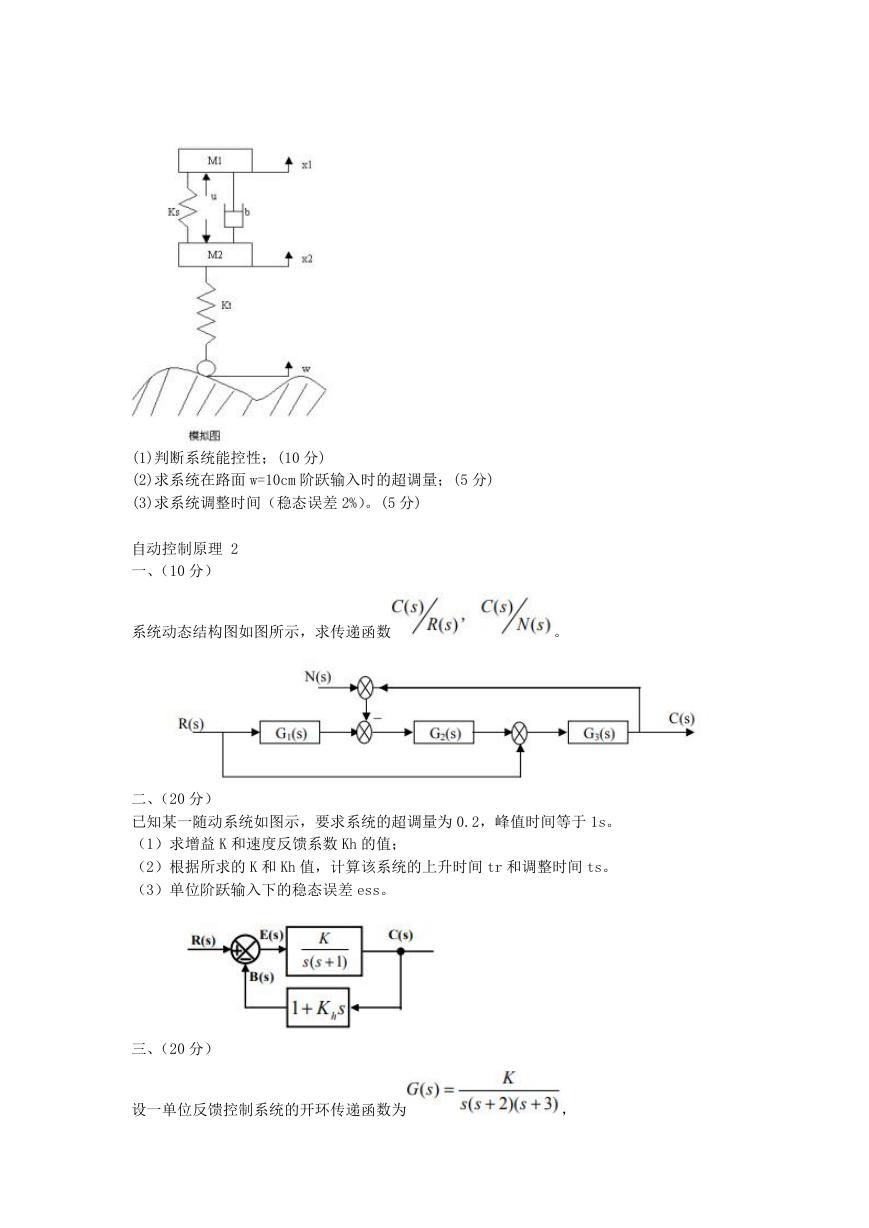
七、（20 分）已知一采样系统如图 4 所示，其中采样时间 T=1s。试求： (1)开环脉冲传递函数 C )； (2)闭环脉冲传递函数 C )； (3)闭环系统稳定的 k 值范围。 ( R ( ( ( E z ) z z z ) 八、（20 分）已知系统的状态空间表达式为： (1)画出系统的状态图；(8 分) (2)试将状态方程化为对角标准形。(12 分) 九、（20 分）如图所示，车身质量：M1=1500kg，簧下质量：M2=320kg，悬架弹簧刚度： Ks=10000N/m，悬架阻尼系数：b=140000N.s/m，轮胎刚度：Kt=10Ks，已经设计了状态反馈控制器 u  Kx,可将系统极点配置在，状态表达式如下，

(1)判断系统能控性；(10 分) (2)求系统在路面 w=10cm 阶跃输入时的超调量；(5 分) (3)求系统调整时间（稳态误差 2%）。(5 分) 自动控制原理 2 一、（10 分）系统动态结构图如图所示，求传递函数。二、（20 分）已知某一随动系统如图示，要求系统的超调量为 0.2，峰值时间等于 1s。（1）求增益 K 和速度反馈系数 Kh 的值；（2）根据所求的 K 和 Kh 值，计算该系统的上升时间 tr 和调整时间 ts。（3）单位阶跃输入下的稳态误差 ess。三、（20 分）设一单位反馈控制系统的开环传递函数为，

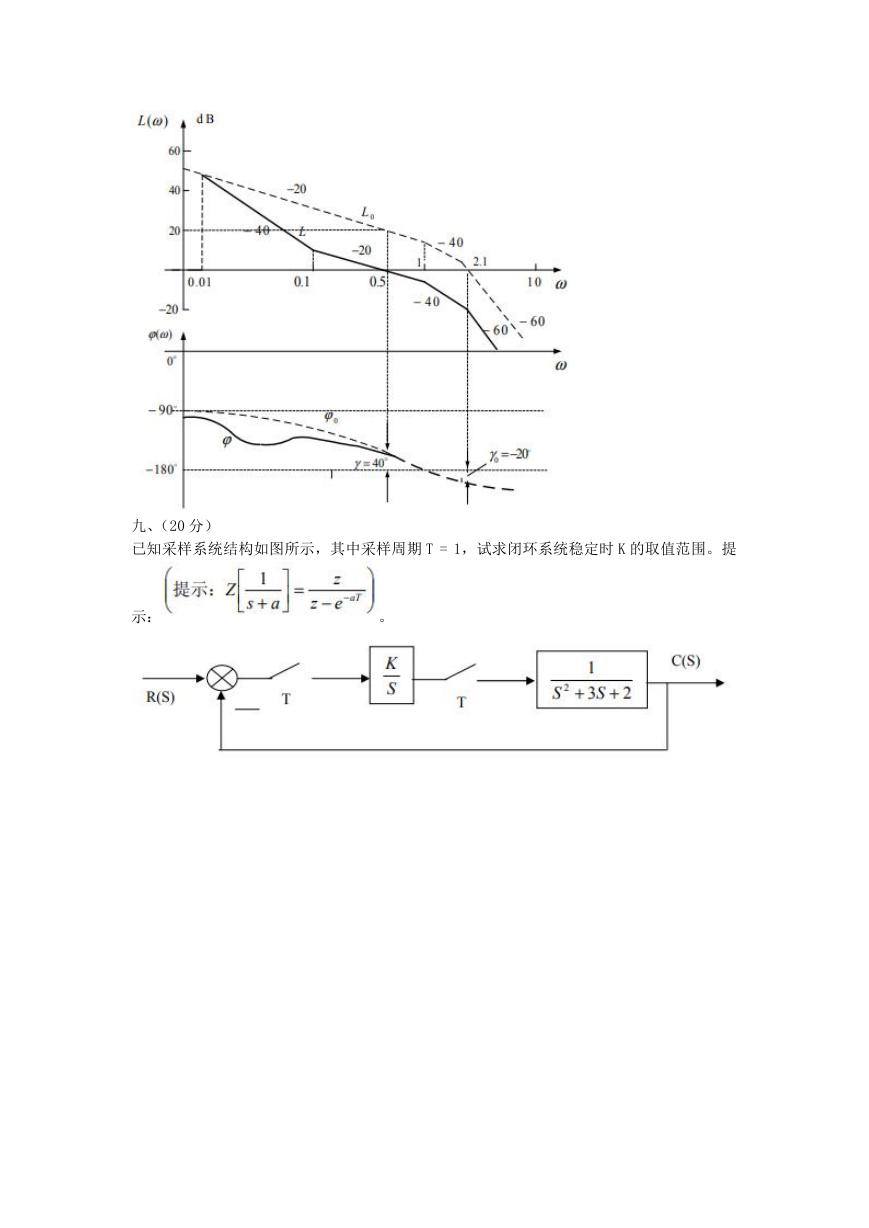
（1）绘制系统根轨迹；（2）求产生重根和纯虚根的 K 值（3）分析 K 值对系统性能的影响。四、（15 分）画出的奈氏图，判断其闭环系统的稳定性。五、（15 分）（1）简述对控制系统性能的基本要求，以及评判系统性能的指标有哪些？（2）控制系统的典型输入信号有哪几种？试写出其数学表达式。六、（15 分）试绘制该系统的设某控制系统的开环传递函数为 Bode 图，并确定剪切频率 wc 的值。七、（15 分）一单位反馈控制系统的开环传递函数为（1）求系统的静态误差系数；（2）当输入八、（20 分）时，求系统的稳态误差。设一系统的开环传递函数为：，伯德图如图中虚线所示，实线为校正后的系统的伯德图。 (1)对系统采用了哪类校正方法？ (2)写出校正环节的传递函数。 (3)画出校正环节的伯德图。

九、（20 分）已知采样系统结构如图所示，其中采样周期 T = 1，试求闭环系统稳定时 K 的取值范围。提示：。

分享到：

赞收藏

资料库

2015年浙江省中国计量大学自动控制原理考研真题.doc

相关推荐

考研

热门标签

最新资料