2017年A题-CT 系统参数标定及成像——黄璐哲等(浙江大学,本科组MATLAB 创新奖获).pdf-资料库

tcliuxq02-10591951-16359648102813657787.pdf-第1页.png

第1页 / 共47页

tcliuxq02-10591951-16359648102813657787.pdf-第2页.png

第2页 / 共47页

tcliuxq02-10591951-16359648102813657787.pdf-第3页.png

第3页 / 共47页

tcliuxq02-10591951-16359648102813657787.pdf-第4页.png

第4页 / 共47页

tcliuxq02-10591951-16359648102813657787.pdf-第5页.png

第5页 / 共47页

tcliuxq02-10591951-16359648102813657787.pdf-第6页.png

第6页 / 共47页

tcliuxq02-10591951-16359648102813657787.pdf-第7页.png

第7页 / 共47页

tcliuxq02-10591951-16359648102813657787.pdf-第8页.png

第8页 / 共47页

畃畔系统标定与图像重建摘要为解决畃畔系统参数标定及成像问题，本文由相关理论基础入手，剖析模板形态学特征，以此为切入点建立并优化了标定模型，并且对根据未知介质进行图像重建，根据图形特性实现了噪声去除。针对问题一，我们根据基础理论知识，结合几何计算，得出标定模型在各个照射角度中的投影强度表达式，尝试通过函数拟合的方法求解。在扫描图中，圆和椭圆的投影函数相互耦合，为了更好的将其区分开，我们从图像处理的角度入手，通过高通滤波和形态学操作大致提取出椭圆曲线边界，利用其宽度信息粗略求出各次投影的角度。再利用粗测的角度，计算出圆的轨迹，挖去受圆形投影影响的数据点，以此来消除圆的投影函数对椭圆投影函数的影响，用剩下的数据对椭圆投影曲线进行拟合，得到了很好的效果，以较高的精度精确计算出畘光各次照射角度及其他标定相关的参数。针对问题二、三，考虑到逆畒畡畤畯畮变化的卷积特性，首先使用线性插值得到新的图像作为逆畒畡畤畯畮变换的输入，再经由坐标变换，内插缩放、滤波变换等操作得到最终的介质吸收率分布图。针对问题四，模型检验部分，我们从误差理论角度进行分析，研究标定模型的敏感性，并尝试人为引入噪声，验证模型的稳定性。在研究过程中我们发现了原定标模型在特定角度附近精度大幅下降的问题，针对该问题，尝试设计出“三角形”标定模板等若干种模板，最终兼顾合理性及稳定性，确定“双椭圆”模板作为新标定模板，从理论上证明其稳定性优于原模版。关键词畃畔系统、畒畡畤畯畮变换、图像处理、最小二乘拟合、插值、滤波由

1 问题重述 1.1 问题背景Ｘ射线是一种能够穿透物体的能量射线，并会产生衰减、折射、散射等物理现象。计算机断层成像用畃畯畭異畵畴略畤畔畯畭畯畧畲畡異畨畹甬畃畔甩技术依据畘射线穿过待测物体发生吸收衰减的原理，可以在不破坏物体内部结构的情况下对其进行三维可视化成像。畃畔技术作为一种重要的无损检测技术，广泛应用于医学成像、工业探伤、货运安检以及文物复原等领域。畃畔技术的发展大致经历四个阶段：第一代畃畔设备通过平行束平移旋转扫描获得投影数据；第二代设备使用小角度扇形射线束代替平行束；第三代设备仅包含扇形束的旋转扫描动作，不再采用平移运动；第四代设备将探测器固定于申甶田◦圆周上，仅旋转畘射线源以解决环形伪像问题。由于被测物与扫描环境的复杂性，畃畔扫描方式日趋灵活。畃畔技术快速发展，对畃畔设备的精密度要求随之提升。由于安装过程中存在误差，实际的畃畔成像系统不满足理想成像关系，会使断层图像的重建质量受到影响。因此，使用畃畔系统前需要借助已知结构的样品进行标定，修正安装误差。 1.2 相关信息典型初代二维畃畔系统如图??所示，探测器平面由电由甲个等距接收点组成，畘射线垂直入射。发射器与探测器相对位置固定不变，探测系统绕固定旋转中心逆时针旋转由甸田次。对每一个畘射线方向，探测器测量经位置固定不动的二维待检测介质吸收衰减后的射线能量，并经过增益等处理后得到由甸田组接收信息。图由町畃畔系统示意图甲

1.3 需解决的问题本文将题述问题归结为以下三个部分，建立数学模型进行分析研究。问题一：参数标定根据标定模板的几何形状与附件由给出的吸收强度，以及附件甲给出的探测器接收信息，标定畃畔系统的相关参数，包括旋转中心的位置、探测器单元间距、畘射线的由甸田个投射角度。问题二、三：CT成像利用已标定的畃畔系统参数，结合附件申、附件电给出的未知介质接收信息进行成像，确定未知介质的位置、几何形状与吸收率等信息，并具体给出附件甴所给位置的吸收率。问题四：模型分析与改进分析问题一中参数标定的精度与稳定性，自行设计新模板、建立对应标定模型以做出改进。 2 问题分析本问题主要研究畃畔系统的参数标定与成像。首先通过投影信息确定畘射线入射角度及探测器单元间距，通过图像重建确定旋转中心位置，完成系统参数标定；其次由投影信息直接重建图像，获取未知介质信息；最后分析参数标定的精度与稳定性，设计新模板并建立标定模型。 2.1 问题一分析问题一，建立投影强度曲线的数学模型。首先分析椭圆投影宽度随畘射线角度的变化规律，以粗略确定各入射角度及旋转中心。在各入射角度对应的投影强度曲线中，通过图像重建去除圆形模板影响的点位，拟合椭圆投影强度曲线，求解增益系数、探测器单元间距、入射角度的关系。其次在原强度曲线中，扣除椭圆投影的影响，得到由甸田组精确的圆形投影强度曲线。拟合圆形投影强度曲线，通过投影宽度求解探测器单元间距，从而精确求解增益系数与畘射线入射角度。最后通过图像重建，确定旋转中心位置。申

2.2 问题二、三畃畔系统的工作原理是由投影重建图像，针对平行束系统的重建算法包括直接反投影法、滤波反投影法、卷积反投影法等，相关文献中已有详细论述。针对问题二应以投影信息与标定所得系统参数作为输入，通过逆畒畡畤畯畮变换重建图像，并对图像进行滤波去噪处理，以得到未知介质的信息。 2.3 问题四分析问题一中参数标定的精度与稳定性，针对确定θ取值时所用的畡畲畣畣畯畳θ函数在极值点附近对误差的敏感性进行改进。提出以斜甴电◦椭圆代替圆形的新模板，建立相应标定模型，对其精度与稳定性进行评估。 3 假设与符号 3.1 模型假设由甮入射的畘射线完全平行，忽略相互干涉。甲甮探测器单元阵列与二维待检测介质处于同一平面中，忽略载物台在任意角度可能发生的倾斜。申甮附件所给接收信息均为精确值。 3.2 符号说明 4 模型建立与求解 4.1 CT成像的理论基础 X射线与物质的相互作用当畘射线照射在被检测物体上时，一部分射线能量被物体吸收，使得射线强度发生衰减。其衰减遵循界畡畭畢略畲畴甭畢略略畲吸收定律畛?畝，呈指数变化。如图??所示，设畘射线初始强度为I0，穿过厚度为x，吸收系数为µ的均匀介质后强度变为I，则有： I 甽 I0e−µx I0 I µx 甽 ln 甴用由甩用甲甩

符号甁d θi a b R D f 用x, y甩 g用s, θ甩符号说明探测器单元间距第i组畘射线的入射方向椭圆半长轴椭圆半短轴圆半径椭圆投影宽度单位 mm rad mm mm mm mm 吸收率函数，表示介质吸收强度的分布投影函数，表示计算所得的投影强度值，畳为真实投影坐标 h用l, θ甩采样函数，表示探测器采样数据拟合所得曲线，畬为像 k kµ 素坐标，为真实投影长度的1/∆l倍增益系数，探测器接收信息与投影强度的比值 mm−1 比例系数，表示由采样信息重建的图像与吸收率数据的比值表由町符号说明对于二维平面内的不均匀介质，吸收系数表示为厚度x的函数µ用x甩，此时界畡畭畢略畲畴甭畢略略畲吸收定律表示为： µ用x甩dx 甽 ln I0 I 用申甩式??表明，畘射线穿过物体后的射线强度与被检测物体的吸收系数相关，畃畔成像的物理本质就是通过探测器接收的强度信息计算吸收系数µ的分布。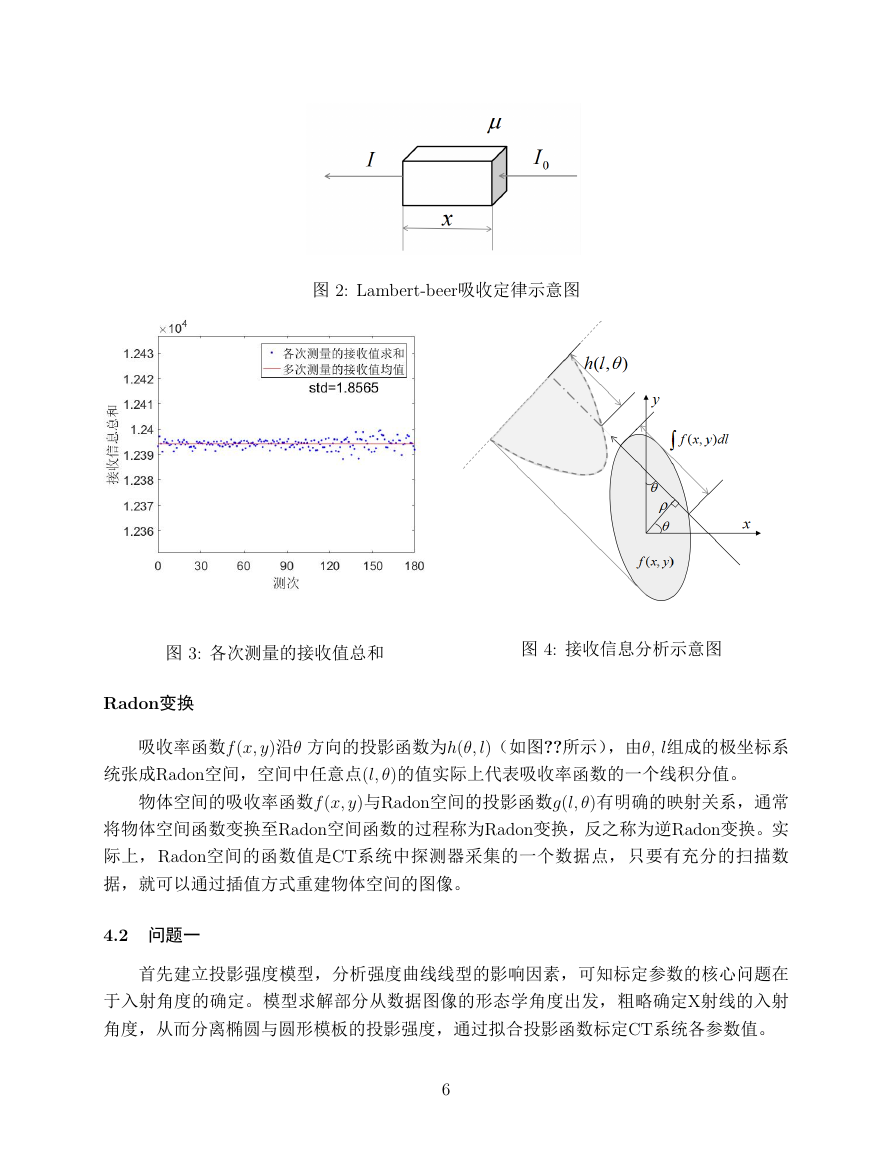数据意义的分析解释相关文献显示，探测器接收的投影信息应与吸收系数µ用x甩沿投影方向的线积分成正比，现有图像重建算法均以此为前提。针对本题所给数据，分析附件由可知标定模板吸收率处处相同；将附件甲中同一入射角度对应的全部接收值求和（如图??所示），可见接收值总和基本保持不变。可以认为，本题所给数据存在类似关系，即探测器接收信息与吸收率函数f 用x, y甩沿畘射线入射方向的线积分（即投影强度）成正比： f 用x, y甩dl 甽由 k h用l, θ甩用甴甩式中h用l, θ甩为探测器接收信息，f 用x, y甩为介质的吸收率分布，k为增益系数。电

图甲町界畡畭畢略畲畴甭畢略略畲吸收定律示意图图申町各次测量的接收值总和图甴町接收信息分析示意图 Radon变换吸收率函数f 用x, y甩沿θ 方向的投影函数为h用θ, l甩（如图??所示），由θ, l组成的极坐标系统张成畒畡畤畯畮空间，空间中任意点用l, θ甩的值实际上代表吸收率函数的一个线积分值。物体空间的吸收率函数f 用x, y甩与畒畡畤畯畮空间的投影函数g用l, θ甩有明确的映射关系，通常将物体空间函数变换至畒畡畤畯畮空间函数的过程称为畒畡畤畯畮变换，反之称为逆畒畡畤畯畮变换。实际上，畒畡畤畯畮空间的函数值是畃畔系统中探测器采集的一个数据点，只要有充分的扫描数据，就可以通过插值方式重建物体空间的图像。 4.2 问题一首先建立投影强度模型，分析强度曲线线型的影响因素，可知标定参数的核心问题在于入射角度的确定。模型求解部分从数据图像的形态学角度出发，粗略确定畘射线的入射角度，从而分离椭圆与圆形模板的投影强度，通过拟合投影函数标定畃畔系统各参数值。甶

图电町吸收率函数及其投影函数 4.2.1 投影强度模型的建立记第i组畘射线入射方向与正方形托盘竖直轴的夹角为θi，探测器位于托盘正下方时θ为田，以逆时针方向为正。记旋转中心为O点，在探测器平面的投影点为Oθ，以此为原点建立投影强度坐标轴（如图??所示），表示物体空间的真实投影坐标，单位为mm。记椭圆中心为O1，圆形中心为O2， O1OOθ 甽 α1，|OO1| 甽 A1， O2OOθ 甽 α2，|OO2| 甽 A2，则O1， O2在Sθ轴上的投影为： so1用θ甩甽 A1 畳畩畮用α1 − θ甩 so2用θ甩甽 A2 畳畩畮用α2 − θ甩用电甩用甶甩首先建立椭圆的投影强度模型。以椭圆中心为基准，计算吸收率的线积分值可得： − 1用s g , θ甩甽甴a2b2 用a2 畳畩畮2 θ 甫 b2 畣畯畳2 θ甩2 2 甫 s 甴a2b2 a2 畳畩畮2 θ 甫 b2 畣畯畳2 θ 于是在sθ轴中，有 g1用s, θ甩甽 g 1用s − so1, θ甩 − 甽甴a2b2 用a2 畳畩畮2 θ 甫 b2 畣畯畳2 θ甩2 用s − so1甩2 甫甴a2b2 a2 畳畩畮2 θ 甫 b2 畣畯畳2 θ 男用男甩用甸甩

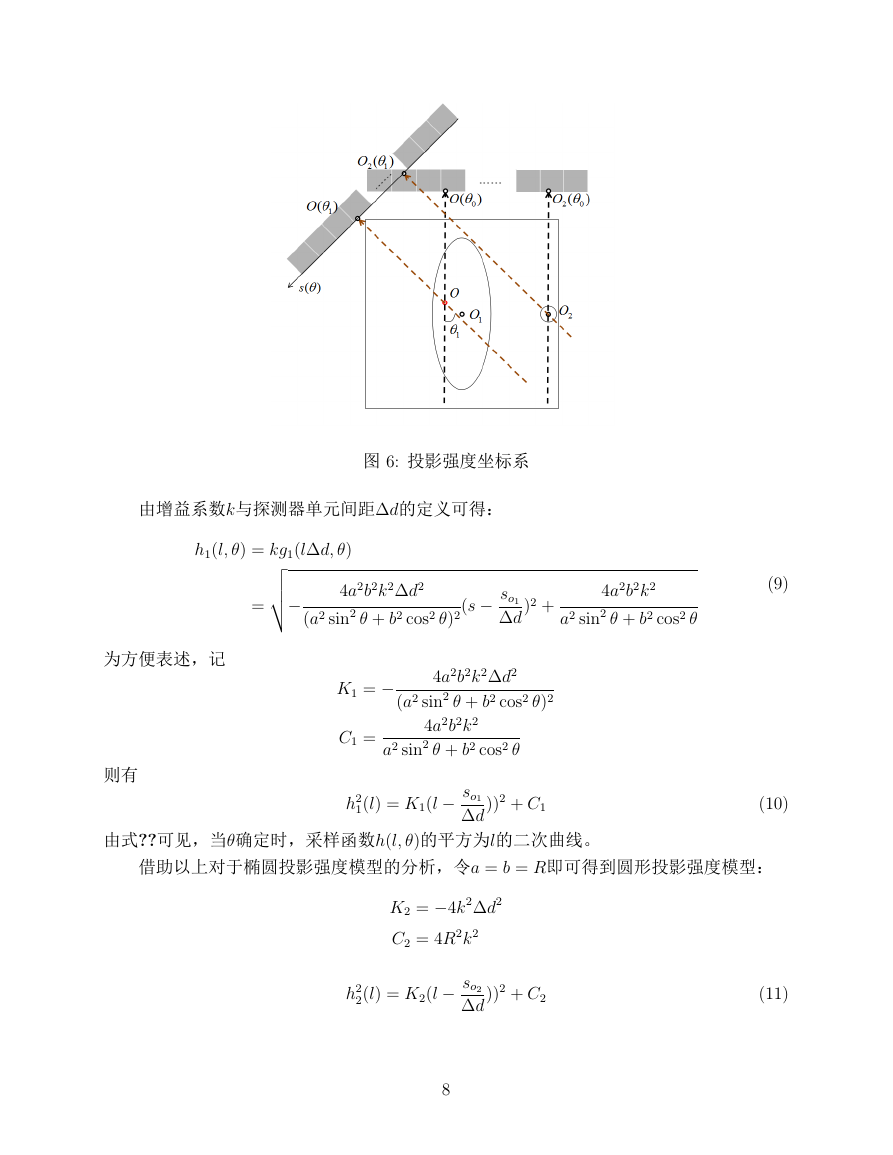
图甶町投影强度坐标系由增益系数k与探测器单元间距甁d的定义可得： h1用l, θ甩甽 kg1用l甁d, θ甩 − 甽为方便表述，记则有甴a2b2k2甁d2 用a2 畳畩畮2 θ 甫 b2 畣畯畳2 θ甩2 用s − so1 甁d 甩2 甫甴a2b2k2 a2 畳畩畮2 θ 甫 b2 畣畯畳2 θ K1 甽 − 甴a2b2k2甁d2 用a2 畳畩畮2 θ 甫 b2 畣畯畳2 θ甩2 C1 甽甴a2b2k2 a2 畳畩畮2 θ 甫 b2 畣畯畳2 θ 1用l甩甽 K1用l − so1 h2 甁d 甩甩2 甫 C1 用甹甩用由田甩由式??可见，当θ确定时，采样函数h用l, θ甩的平方为l的二次曲线。借助以上对于椭圆投影强度模型的分析，令a 甽 b 甽 R即可得到圆形投影强度模型： K2 甽 −甴k2甁d2 C2 甽甴R2k2 2用l甩甽 K2用l − so2 h2 甁d 甩甩2 甫 C2 用由由甩甸

资料库

2017年A题-CT 系统参数标定及成像——黄璐哲等(浙江大学,本科组MATLAB 创新奖获).pdf

相关推荐

行业

热门标签

最新资料